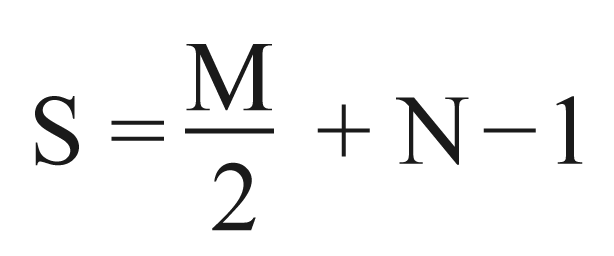Математика: Аянт
Содержание
Аянтты өлчөөнүн тарыхынан
Бизге тарыхтан белгилүү болгондой, мындан төрт миң жыл илгери египеттиктер ар кандай түз сызыктуу фигуралар болгон квадраттын, тик бурчтуктун, үч бурчтуктун жана трапециянын аянттарын туура эсептегенди билишкен. Квадрат өзү жеткиликтүү түргө ээ болгондуктан аянттарды өлчөөнүн калыбы катары кызмат аткарган. Египеттиктер Нилдин ар бир куймасынын тушундагы талааларды алардын чегин табуу аркылуу майда бөлүктөргө бөлүштүрүшкөн. А ал үчүн болсо ар кандай фигуранын аянттарын эсептегенди билиши керек: анткени аянты каалагандай формада болушу ыктымал эмеспи. Өзгөчө талааларды жер иштетүүчүлөрдөн салык жыйнашкан фараондун аткаминерлери өтө тыкат эсепешкен. Жер ченегичтер ченөөчү курал катары чыканактын, алакандын жана манжалардын ченинде белгилен тыгыз керилген аркандарды колдонушкан. Эгерде жер аянтчасы квадрат же тик бурчтук түрүндө болсо, анда аны ченөө оңойго турган. Ал үчүн узунун жана туурасын ченөө менен бирине-бирин көбөйтүп коюушкан. Айталы, узуну он чыканак, а туурасы сегиз дейли. Демек, бул аянтчага 80 чыканактуу жагы бар квадратты жайгаштырса болот. Анын аянты – сексен чарчы чыканак. Арийне, аянтча ар кандай формада болушу мүмкүн. Баардык эле аянтчаларды тик бурчтуктарга бөлө бере албайбыз. А үч бурчтуктуу аянтчаны каалагандай аянтчаларга бөлө берсек болот – эгерде ал тик бурчтуктуу сызыктар менен чектелген болсо. Мындан улам египеттиктерди ар кандай фигурадагы аянттарды эсептөөнүн ыкмаларын жана усулдарын толук кандуу өздөштүрүшкөн десе жаңылыш болбойт. Негизги геометриялык фигуралардын аянттарын эсептеген Нил дарыясынын жээгиндеги байыркы жашоочулардан артта калбаганга аракеттенелик.
Алгач аянт – бул геометриялык фигуранын өлчөмүн мүнөздөөчү чоңдук экенин эсибизге салалык. Башка сөз менен айтканда, ошол геометриялык фигура ээлеген тегиздиктин бир бөлүгү экенин билдирет.
Аянтты ченөөнүн бирдиктүү системасы
ХVIII кылымга чейин аянтты ченөөнүн бирдиктүү системасы болгон эмес. Кайсы бир өлкөлөрдө узундук чыканак менен, а кайсы бир өлкөлөрдө болсо таман менен ченешкен. Биздин тарыхыбызда белгилүү болгондой, биздин ата-бабаларыбыз боз үйдүн аянтын (тегерете аянтчасын), эшигинин, айдоо жерлерди, жайыттарды жана чабууга ылайыктуу жерлердин аянтын, таш короолордун, чырпык-короолордун, койлорду камап коё турган бадалдардын аняттарын да эсептешкен. Аларды ченөөдө өтө татаал эмес чен бирдиктери колдонушкан: алакандай, үйдүн ордундай, тапан, теше сыяктуу.
Ченөөнүн же эсептөөнүн мындай ыкмасы өтө ыңгайсыз болгон, ал болсо өлкөлөр менен соода-алаканын өнүгүшүнө кыйла тоскоолдук жараткан.
Ошондуктан жалпы жаңы ченөөнүн бирдиги кабыл алынган жана бул оңойго турбаган ишти фрунцуз окумуштуулары жоопкерчиликти моюндарына алышкан. Жалпы ченөөнүн системасынын негизинде “баардык мезгил үчүн жана баардык элдер үчүн” деген узундук бирдиги жатаарын чечишкен. Ал эмне деген узундук? Жер шарынын полюсунан экваторго чейинки аралыкты аныкташып (мунун оңойго турбаганын байкайбыз), ал аралык 10 000 000 го бөлүнгөн. Алынган чоңдукту узундукту ченөөнүн бирдиги катары кабыл алышып, ага – метр деген ат беришкен, ал сөз грекчеден которгондо “ченөө, өлчөм” дегенди билдирген. 10 саны метрдин бөлүкчөлөрү үчүн негиз болуу аркылуу километр, дециметр, сантиметр жана миллиметр түшүнүктөрү келип чыккан. Аянтты ченөөнүн негизги бирдиги катары чарчы метр эсептелинген, андан сырткары да: чарчы километр, гектар, ар (сотка), чарчы дециметр, чарчы сантиметр, чарчы миллиметрлер бар.
Аянттын бирдигинин ортосундагы дал келүүчүлүк
Аянтты ченөө бирдиктерин алардын кемүү тартибинде жайгаштырып көрөлү: чарчы километрден тартып чарчы миллиметрге чейин. Ченөөнүн ар бир коңшу бирдиктери өтмөк катары ченөөнүн кичине бирдигин көбөйтө турган 100 санынан турат, а тескерисинче чоң бирдик болуп калса 100гө бөлүүгө туура келет. Эгерде бирдикти которууга коңшу эмес бирөөнөн кийинки (же мурдагы) бирдик туура келсе, анда эки жолу өткөрүүнү аткарууга керек. Үчүнчү бирдикке – үч жолу өткөрүү керек. Бул учурда өткөрүүчү сан биздин жолубузда кездеше турган бирдик жана нөлдөрдөн куралган сан болуп эсептелинет. Солго карай өткөрүүдө (б.а. чоң бирдикке карай) бөлөбүз, ал эми оңго карай өткөрө турган болсок (б.а. кичине бирдикке карай) – көбөйтөбүз.
Мисалы, 1мм2 ты 1 м2 ка өткөрсөк 3 өткөрүү солго карай, демек 1ди 1 000 000го бөлөбүз. 1:1 000 000=0,000001ди алабыз. Демек, 1мм2 = 0,000001 м2.
Аянттын бирдиктеринин ортосундагы катыштарды эске түйүп калуу үчүн, төмөнкү эскертмени сунуштайбыз. Муну кагазга бастырып чыгарып алып үй тапшырмасын аткаруу учурунда пайдалансак болот. Албетте, бул адбан пайдалуу, эгерде бир ченөө бирдигинен башка чен бирдигине өтүүнү кандай жүргүзүүнү эске түйүп алсаң.
Байыркы Вавилондо тик бурчтуктун аянтын эсептегенди билишкен мезгилде, байыркы египеттиктер ар түрдүү фигуранын аянтын (баары эле эмес, өтө чоң эмес тегеректөө менен) ошол эле ыкмага окшош ыкманы колдонуп силер менен биз сыяктуу эсептей алышкан. Ал эми байыркы грек математиги Евклид (б.з.ч. 300 ж. чамасы) өзүнүн “Башталыш” аттуу көп томдуу эмгегинде (геометрияга арналган 13 китептин 10унда) көптөгөн геометриялык фигуралардын аянттарын эсептөөнүн жетишээрлик көптөгөн ыкмаларын сунуштаган. Орустардагы геометриялык маалыматтарды камтыган алгачкы жазмалар (чынында, практикалык өңүттө) XVI кылымдарга туура келет. Анда түрдүү формадагы фигуралардын аянттарын ченөөнүн эрежелери жыйналган.
Геометриялык фигуралардын негизги аяныттык формулалары
Азыркы мезгилдин математикасы алдыга карай алыс кадамын таштады десек болот, буга далил, азыр мүмкүн болгон керек болсо түз эмес сызыктар менен чектелген фигуралардын аянттарын жогорку тактыкта табууга болот. Арийне, биз негизги деген: үч бурчтук, тик бурчтук, квадрат, параллелограмм, ромб, трапеция жана тегерек сыяктуу геометриялык фигуралардын аянттынын формулалары менен гана таанышабыз. Бул кайсы фигура экендигинин түшүндүрмөсүн биздин глоссарийден, ал эми формуласын – ыңгайлуу таблицадан тапсаңар болот. Кагазга бастырып чыгарып алып, жаттагыла жана пайдалангыла!
Төрт бурчтуктун аянтын өлчөө
Эмне кылыш керек...
Эгерде беш жана андан көп бурчтары бар көп бурчтук берилсе, эмне кылуу керек? Албетте, аны эсептегенге оңой болгондой кылып – тик бурчтук, үч бурчтук, трапеция, параллелограмм сыяктуу жөнөкөй фигураларга бөлүү керек. Көп бурчтуктардын таң калаарлыктай касиеттерин австриялык математик Георг Пик таап чыккан. Ал, чокулары квадраттык торчонун түйүндөрүндө жайгашкан көп бурчтуктарды төмөнкү формула боюнча тапса болоорун аныктаган:
мында S — көп бурчтуктун аянты;
N — көп бурчтуктун ичинде жайгашкан торчонун түйүндөрүнүн саны;
M — көп бурчтуктун жактарына жана анын чокуларынан дал келген торчонун түйүндөрүнүн саны.
“Түйүн” түшүнүгү сызыктардын кесилишкен жери.
Биринчи мисалда биздин ABCD төрт бурчтугунун аянты 24,5ке барабар. Мындан, Пиктин формуласы боюнча тынак чыгарсак, туура жообун алабыз. Андан сырткары, ал торчо барактагы көп бурчтуктардын аянттарын эсептөөдө башка дагы ыкмаларын көрсөтүүгө да түрткү берет:
- көп бурчтуктун аянтын эсептөө үчүн, болгону бул формуланы билүү зарыл:
- Пиктин формуласы эң жөнөкөй жана эстегенге да ыңгайлуу. Колдонууда да өтө ыңгайлуу жана жөнөкөй. А аянттарын эсептей турган көп бурчтук каалагандай керек болсо акылың жеткен формада да болушу мүмкүн.
Глоссарий
Тик бурчтук — бардык бурчтары тик болгон (90 градуска барабар) төрт бурчтук .
Квадрат — бардык бурчтары жана жактары барабар болгон төрт бурчтук.
Параллелограмм (грекчеден. лат. παραλληλόγραμμον παράλληλος — жарыш жана γραμμή — сызык) — бул карама-каршы жактары жарыш, б.а. жарыш сызыктарда жатышкан төрт бурчтук.
Ромб (грекчеден ῥόμβος, лат. rombus, түз которгондо: «бубен») — бул баардык жактары барабар болгон параллелограмм.
Трапеция (грекче. τραπέζιον — «отургуч»; τράπεζα — «стол, трапеза») — эки жагы жарыш, а башка эки жагы жарыш эмес болгон томпок төрт бурчтук. Карама-каршы жактары жарыш болгон жактарын трапециянын негиздери, а башка эки жагын – каптал жактары деп атайбыз. Ортоңку сызыгы – каптал жактарын ортосунан бириктирип турган кесинди.
Үч бурчтук — бир чекитте жатпаган үч чекиттер аркылуу биригип турган үч кесиндиден куралган геометриялык фигура. Көрсөтүлгөн үч чекит үч бурчтуктун чокулары, а кесиндилер – үч бурчтуктун жактары деп аталат. Үч бурчтуктун жактары үч бурчтуктун үч бурчунун чокулары аркылуу туташышат.
Тик бурчтуу үч бурчтук — бир бурчу (90 градуска барабар) тик болгон үч бурчтук.
Тегерек — анын борбору деп аталган чекитке чейинки аралыкта ал тегеректин радиусу деген ат менен берилген терс эмес сандан ашпаган тегиздиктеги чекиттердин геометриялык орду. Эгерде радиус нөлгө барабар болсо тегерек чекитти мүнөздөйт.
Радиус — тегеректин борборун анын чеги менен туташтыруучу кесинди.
Диаметр — тегеректин борбору аркылуу өткөн эки чекиттин туташтыруучу кесинди.
Тегеректин сектору — жаача жана эки радиус менен чектелип, жаачалардын аягын тегеректин борбору менен туташтыруучу тегеректин бир бөлүгү.
Пайдалуу шилтемелер
Маселенин чыгарылышына карата пайдалуу аргумент
Адамзаттын мээси ушунчалык таң калаарлык, аны кызыксыз, жадатма нерселер менен алаксытып таптакыр болбойт, дайыма ажайып кызыктуу гана маселелер менен алектентип туруу зарыл. Силер сурасаңар, эмне үчүн деп? Жообу эң жөнөкөй. Маселелерди чечүү менен, өзүбүздүн мүмкүнчүлүктөрүбүздү талдоого үйрөнүү аркылуу, бир нече чыгарылышын табуу жөндөмүн өнүктүрүп, натыйжада жыйынтыкка келүүнүн эң кыска жолун тапкага жетишебиз.
Эгерде силер дайыма математикалык олимпиадаларга катышып жана татаал математикалык тапшырмаларды жеңил эле чыгарып койгон классташтарыңды көрө албаган көз карашта карап жүргөн болсоң, анда бул оюн-конкурсу силер үчүн. Каалаганыңар өзүңөрдүн мүмкүнчүлүгүңөрдү текшерип, логикалык жактан ой-жүгүртүп, жыйынчактуу жана бекем болууңарга жардам берет. [Электрондук ресурс] // Центр «Снейл» , 2005-2017.URL: https://nic-snail.ru/ (кайрылуу датасы: 20. 11. 2017)
Көпчүлүк окуучуларга “Кенгуру” эмне экенин түшүндүрүүнүн зарылчылыгы жок – бул “Математика баары үчүн” ураанынын алдындагы эл аралык математикалык оюн-конкурсу. Конкурстун негизи максаты – көпчүлүк балдарды математикалык маселелерди чыгара алууга, ар бир окуучуга көрсөтүп, маселе чыгаруунун жөн эле иш эмес жандуу иш экендигин, көңүлдүү экенин керек болсо шаңдуу-шайыр экенин ачып көрсөтөт!. [Электрондук ресурс] // Кенгуру 1995-2017. URL: http://mathkang.ru/ (кайрылуу датасы: 20. 11. 2017)
Мында окуучулар өздөрүнүн билимдерин текшерип эле эмес, өзүн мугалим катары да сынап – өзүнүн тесттерин да түзсө болот! Өзүнөр тапшырмалардын түрүн жана татаалдык деңгээлин тандайсыңар. Бул тесттер Интернет аркылуу эле эмес да иштейт. Ошол эле сыяктуу интернетке мүмкүнчүлүгү жок деле иштесе болот. Каалаган түзүлүштөр жана каалаган аракет системасы аркылуу. Баардык мүмкүнчүлүктөрдү байкап көргүлө жана баалагыла! [Электрондук ресурс] // TestEdu.ru 2013-2017. URL: http://testedu.ru(кайрылуу датасы: 20. 11. 2017)
Библиография
- В.А. Гусев, А.Г. Мордкович Математика. Сурап-билүү материалдары М.: Просвещение, 1988.
- Депман И.Я. Математиктердин тарыхынан. Либроком, 2010. – 152б.
- Федин С. Н. Математиктер да тамашалайт. — 4-чыг. — М.: УРСС, 2012. — 216 б.
- Кыргыздарын ченөө жана эсептөө системалары.: [Электрондук ресурс] //Open.kg Открытый Кыргызстан. URL: https://www.open.kg/about-kyrgyzstan/culture/ethnography/1970-sistemy-izmereniya-i-schet-u-kyrgyzov.html . (кайрылуу датасы: 20.11.2017)
- «Снейл» борбору – Балдар жана педагогдор үчүн массалык түрдө аралыктан билим берүү курстары : [Электрондук ресурс] // «Снейл» борбору , 2005-2017.URL: https://nic-snail.ru/ (кайрылуу датасы: 20. 11. 2017)
- “Кенгуру” Эл аралык математикалык конкурсу. : [Электрондук ресурс] // Кенгуру 1995-2017. URL: http://mathkang.ru/ (кайрылуу датасы:20. 11. 2017)
- «Билим берүү тесттери» долбоору. : [Электрондук ресурс] // TestEdu.ru 2013-2017. URL: http://testedu.ru (кайрылуу датасы: 20. 11. 2017)
- Тик бурчтуктун аянтын кантип табабыз? : [Электрондук ресурс] // КакИменно.ру, 2017. URL: http://kakimenno.ru/raznoe/95-kak-nayti-ploschad-pryamougolnika.html (кайрылуу датасы: 20. 11. 2017)
- Формула Пика. Статья Александра Крутицких. : [Электрондук ресурс] // "Математика? Жеңил!!!" долбоору. URL: https://matematikalegko.ru/formuli/ploshhad-figury-na-liste-v-kletku-formula-pika.html (кайрылуу датасы: 20. 11. 2017)
ул аянт чарчы бирдиктер менен өлчөнөт экени белгилүү. Алар өлчөнгөн аянттын өлчөмүнө жараша болот. Албетте, баары бир бирдикте ченелсе, арийне, мунун натыйжасында сандардын кабыл алуу үчүн өтө эле аз же өтө эле көп болот.
Жер аянтчаларынын көпчүлүгү соткалык түрдө көрсөтүлөт. Бир сотка – бул 100 чарчы метрди көрсөткөн 10 метрге 10 метрди көрсөткөн аянт эсептелинет, ошондуктан сотка деп аталат. Мына жер аянтчаларынын өлчөмдөрүнө мүнөздүү болгон бир нече мисалдар булар:
Келечекте тик бурчтуу аянтын кантип табуу керектигин унутуп калсаңар, эски-эски анекдотту эсиңерге салсаңар. Чоң ата сурап атат бешинчи класстын окуучусунан Ала-Тоонун аянтын кантип тапса болот деп, ал болсо айтат дейт, Ала-Тоонун узунун Ала-Тоонун туурасына көбөйтүп дептир.
Математика, алардын курчап турган дүйнөнү изилдөө үчүн адамдын каалоосу менен бир эле мезгилде пайда болгон. Алгач, азыркыдай астрономия, физиканын катарындагыдай дисциплина катары эмес филосифиянын бир бөлүгү болуп саналган. Арийне, бара-бара кырдаал өзгөрүлгөн. Адамдардын билимдери топтолуп көбөйө баштагандан улам натыйжада, так илимдери менен табигый илимдердин бөлүнүшүнө алып келди. Расмий түрдө “жаралуудан” кийин ар бири өз алдынча өнүгүү жолуна түшүү менен практика менен бекемделген теориялардын пайдубалы өнүгө баштады. Илимдердин эң абстрактуусу болгон математикада кайдагы практика? Бул предмет билим боюнча болуп жаткан баардык иштерди сүрөттөп жана биздин планетадагы жана анын чегинен сырткары да кубулуштардын табияты тууралуу жыйынтык чыгарууга жана алдын алууга мүмкүндүк берет. Мындан улам, баардык илимдер бири-бири менен байланышта десек болот, өзгөчө көз карандык математика менен физиканын ортосунда байкалат. Ошондуктан көпчүлүк окумуштуулардын тобу математик менен физиктер түзөт. Өзүңөр ойлоп көргүлө, бир нерсеге негиздеме бербей туруп кантип түшүндүрмө бере алат? Адамзат тарыхы - бул жаңы аймактарды гана ээлик кылуу эмес, биринчи кезекте өз кызыкчылыгыбызга карай умтулуу керек, ошондой эле көрсөтүп, түшүндүрүп берүүгө арналган чексиз илимий эсептөөлөрдү үйрөнүү жана эртеңки келечекти билүү болуп саналат. Азыркы мезгилдин ачылыштары үчүн кыртыш даярдаган өткөн мезгилдин улуу математиктери кимдер? Таанышкыла!
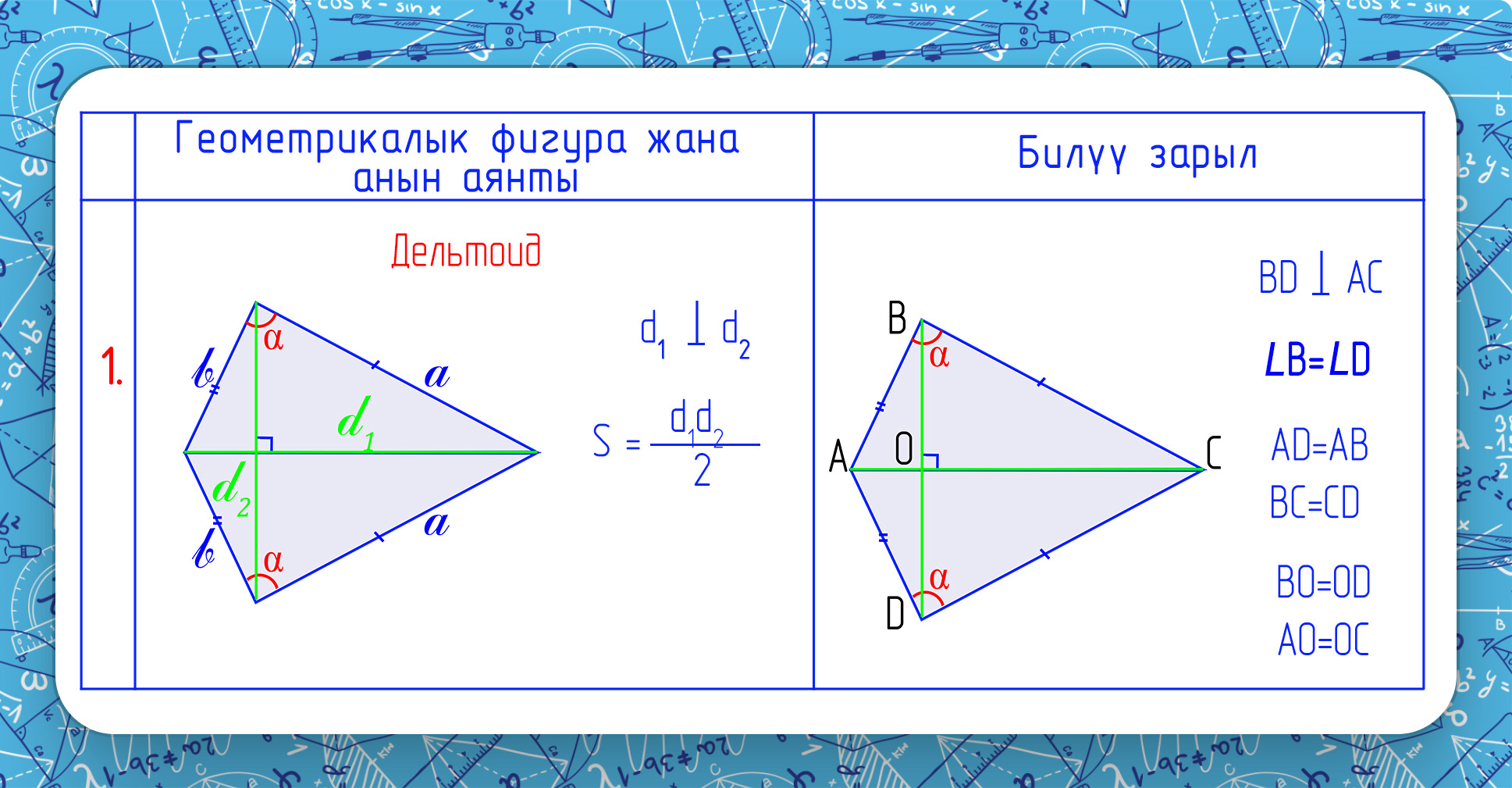
Дельтоид (от др.-греч. δελτοειδής — «далы мүнөздүү», дельта баш тамгасына окшош) — чектеш эки тең жагы бар төрт бурчтук. Кадимки мектеп маалымдагыч жана окуу китептери дельтоид жөнүндө маалыматты камтыбайт экен. Арийне, бул фигураны айлана-чөйрөдө өтө көп кездештиребиз:
Силер билесиңерби, болгону тик бурчтуктун аянтын табуунун формуласын билүү менен жөн гана параллелограмм, ромб, трапеция жана үч бурчтук сыяктуу фигуралардын аянттарын табууга болоорун? Жок? Анда эмесе, “Фигуранын аянты” видеоролигин көрсөң болот.
Демейде биз салтуу турмушубузда математиктерди тажатма кемпай же реалдуу турмуштан таптакыр алыс калган же келесоо чалыш деп элестетебиз. Бул жогорудагы эки учур тең анчалык тамашадай сезилгени менен таптакыр коошпогон нерселер. Деги эле “математика жана тамаша” сөздөрүнүн айкалышы апыртмалуу сезилет. Арийне, бул андай эмес, чындыгында метематикалык тамаша сен ойлогондон дагы өйдө турат. Анын үстүнө чындыгында математикалык тамаша ар тараптуу жана өтө такталган нерсе болуп эсептелинет.
