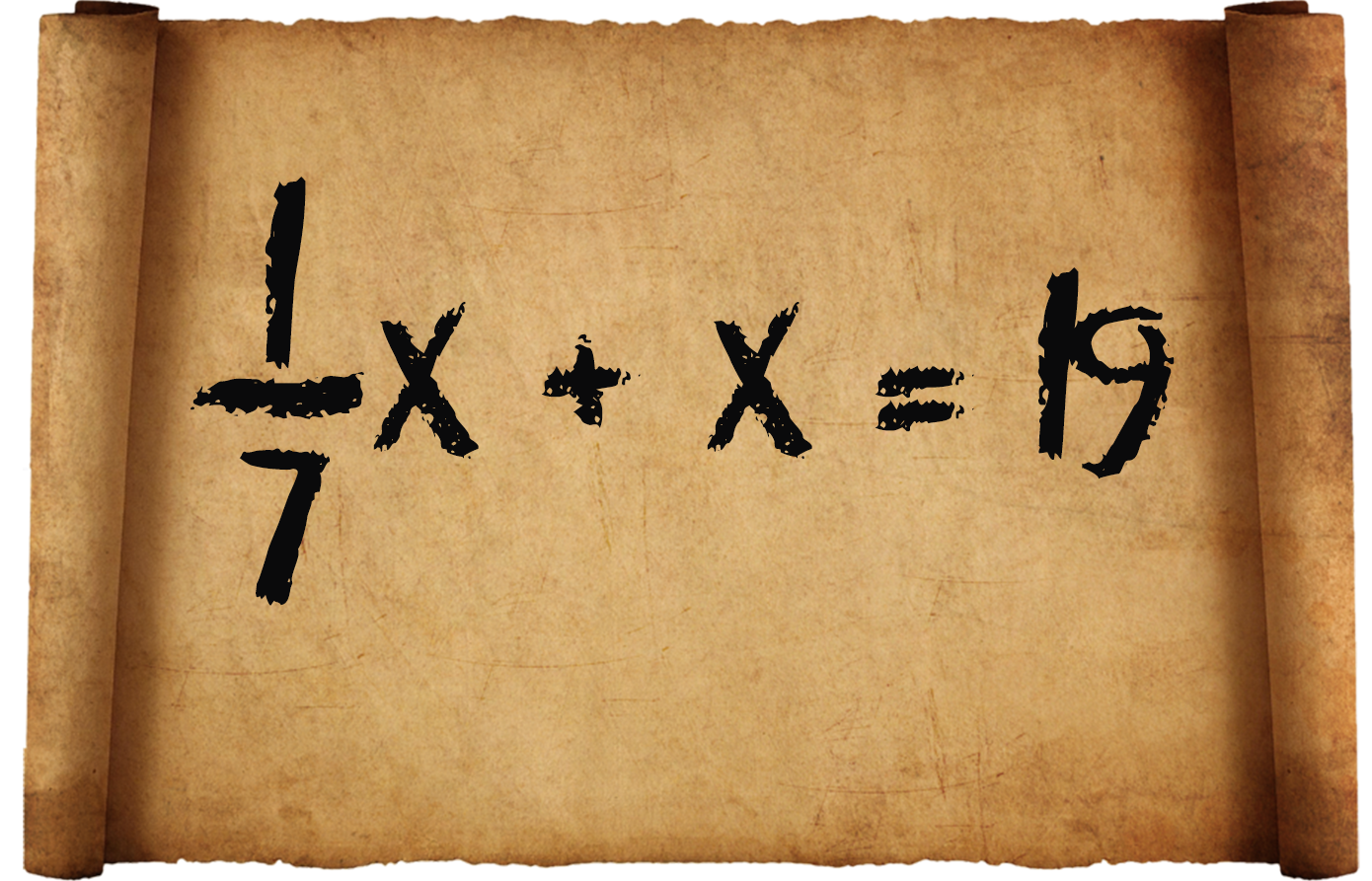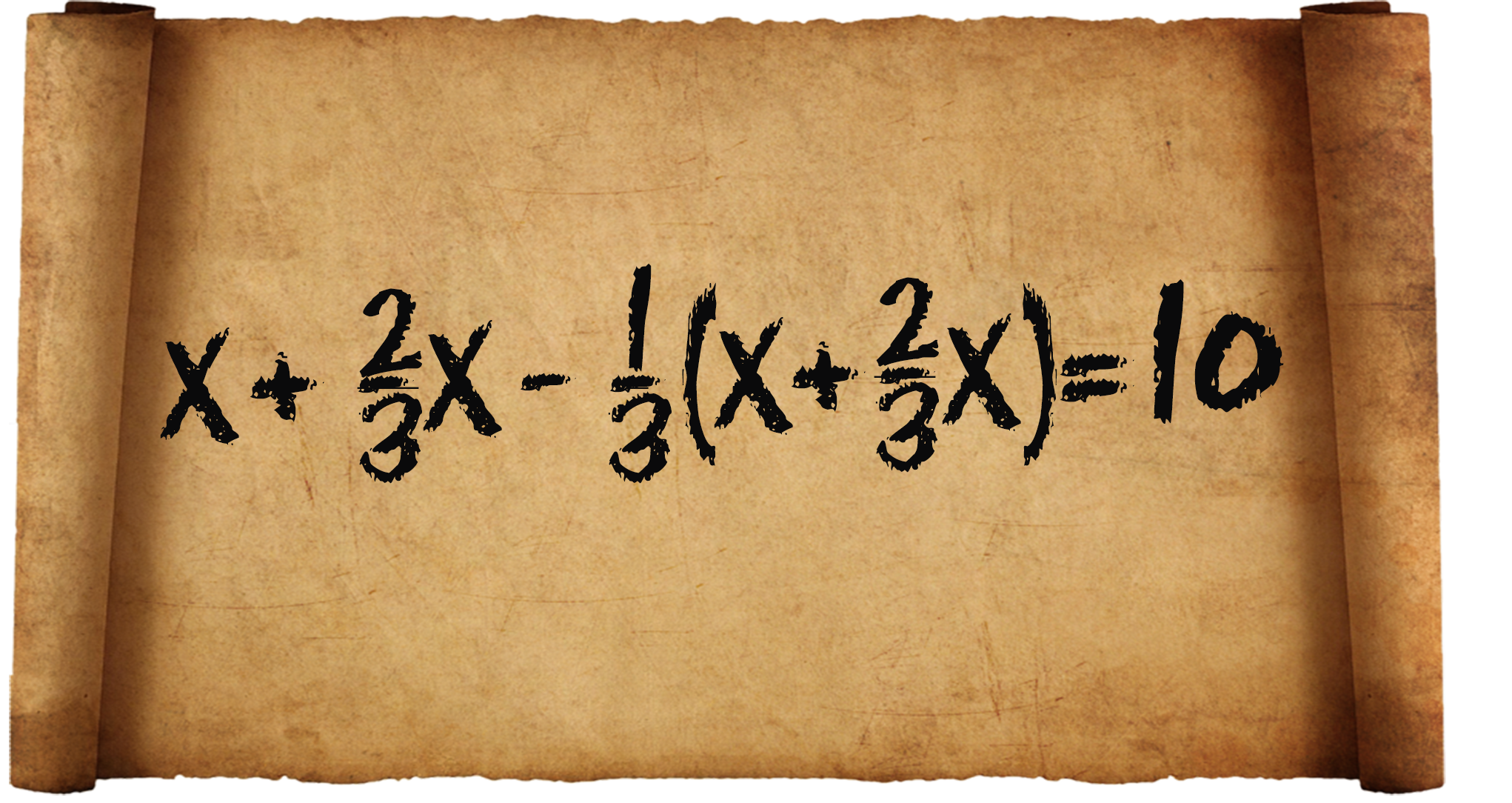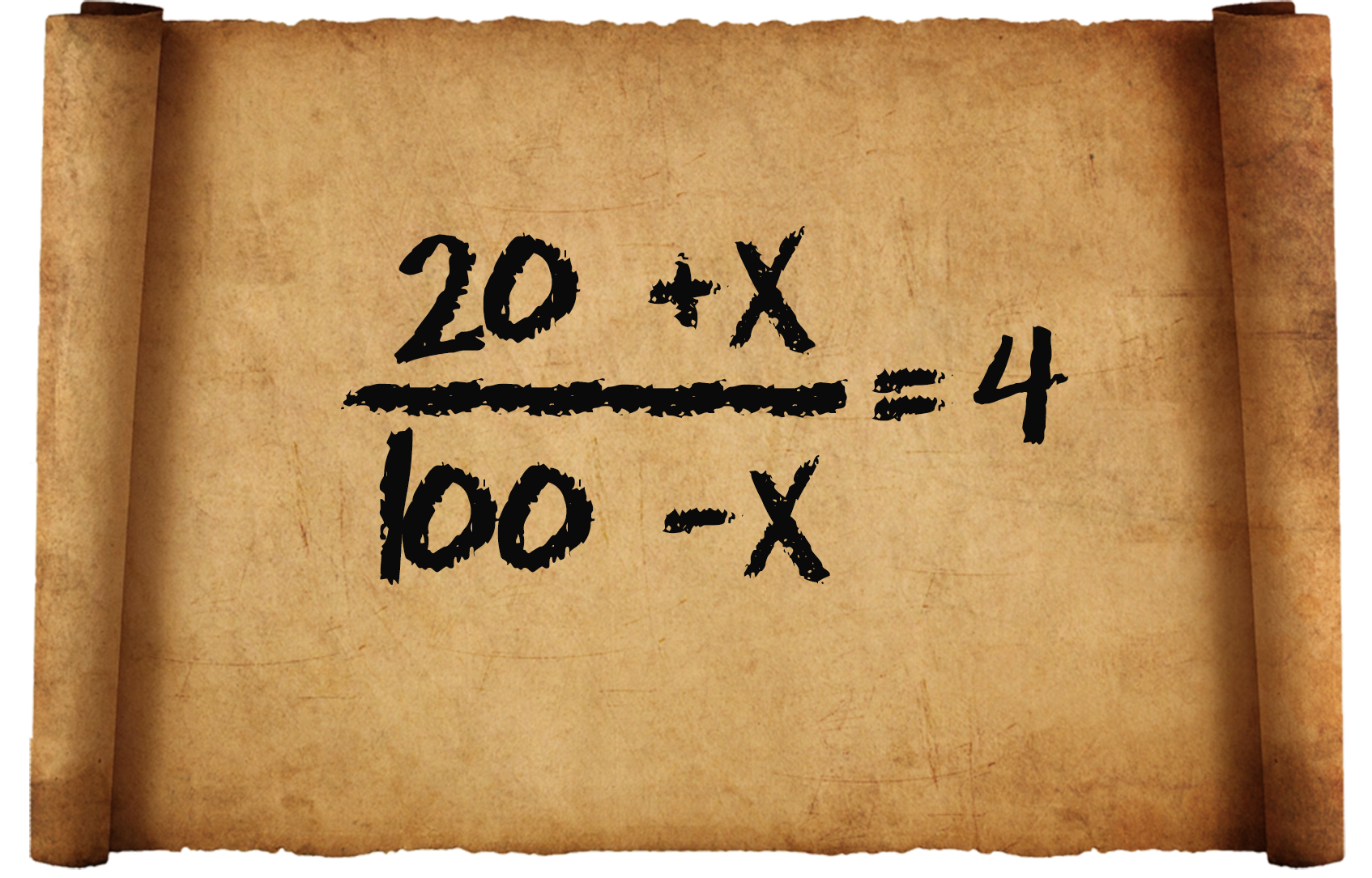Математика: Теңдемелердин чыгарылышы
Содержание
Теңдемелердин тарыхынан
Тендемелер мен үчүн маанилүү,
анткени саясат – азыркы учур үчүн,
а теңдемелер – түбөлүк үчүн.
Альберт Эйнштейн.
Эң байыркы математикалык жазылмаларда эле амалдардын жардамы менен чыгарылган мисалдар жана амалдар кездешкен. Мындай Египеттик папируста биздин заманга чейин 2000 жыл мурун ( анда автор Ахмес жазгыч көрсөткөндөй, бул математикалык жазылмалар мындан да байыркы башка жазылмалардын көчүрмөсү) белгисиз санды табууга маселелери болгон. Ал белгисиз «хау» (дөбөчө) деп аталган жана өзгөчө иероглиф менен белгиленген.
Мына ал папирустун мисалдарынын чыгарылыштарынан:
1) «Белгисиз, анын жетинчи бөлүгү, анын бүтүнү 19ду тузөт».
Азыркы кезде бул мисал мындайча жазылат:
2) «![]() кошулган жана
кошулган жана ![]() алынган: калдыгы 10».
Папируста маселенин чыгарылышын мындайча түшүнсө болот: белгисизге
алынган: калдыгы 10».
Папируста маселенин чыгарылышын мындайча түшүнсө болот: белгисизге ![]() тү кошуп, андан
тү кошуп, андан ![]() алынган, келип чыккан суммадан; калдыгы 10; санды табуу керек.
Азыркы кезде бул маселе мындайча жазылат:
алынган, келип чыккан суммадан; калдыгы 10; санды табуу керек.
Азыркы кезде бул маселе мындайча жазылат: ![]() ; Жообу: х=9
; Жообу: х=9
3) Диофантада дагы бир белгисизи менен амалдар кездешет, мисалы: “20 жана 100 сандары. Бир эле санды эң кичине санга кошуп жана эң чоңунан алуу; сумманын айырмага карата мааниси 4 кө барабар”.
4) Индиялыктардын биздин заманга чейинки VII жана VIII кылымдардагы арифметикалык кол жазмаларында, ал дагы андан дагы байыркы (III-IVкылымдардагы) кол жазманын көчүрмөсү, анда мындай маселе бар:
“Төрт курмандыктын экинчиси биринчиге караганда экиге көп берди, үчүнчүсү экинчиге караганда үчкө көп, төртүнчү үчүнчүдөн төрткө көп, баары биригип 132 беришти. Биринчи канчаны берди?”
Теңдемени жазсак: x+2x+6x+24x=132
Кол жазмаларда бул маселе “жалган абал” ыкмасы менен чыгарылат. (Бул ыкманы Л.Ф.Магницкий өзүнүн “Арифметикасында” пайдаланган.)
“Эгерде биринчи 1ди берсе, анда экинчи 2ни, үчүнчү 6, төртүнчү 24, баары чогуу 33. Бирок баары бирге 132 болчу да, башкача айтканда төрткө көп. Демек, ар бир курмандык төрткө көп беришкен”. Жооп: 4;8;24;96.
Бирок биринчи даражадагы бир белгисизи менен теңдемени чыгаруунун жалпы эрежесин IX кылымда Мухаммед аль-Хорезми берген.
Өзүнүн “Аль-джебр жана аль-мукабала” аттуу жазылмаларында ал теңдемени чыгаруудагы колдонулган эки абалды берген:
1) “аль-джебр” абалы, эгерде теңдемеде терс (алынуучулар) мүчөсү болсо, анда аларды теңдеменин эки жагынын тең карама-каршы мүчөлөрүнө кошулат, анда теңдеменин баардык мүчөлөрү оң болот.
2) “аль-мукабала” теңдеменин эки жагынан тең бирдей мүчөсү алынат, бул болсо аны жөнөкөйлөткөнгө алып келет.
Мисалы.
Берилди: 5х-17=2х-5.
“аль-джебрды” пайдалансак: теңдеменин ар бир бөлүгүнө 5 менен 17и кошобуз.
Анда: 5х+5= 2х+17 алабыз.
“аль-мукабала”: Ар бир бөлүктөн 2х менен 5 ти алабыз.
Анда: 3х=12 ни алабыз.
Бул жерден х ти табуу оңой болот. x=4
Кыргызстандагы математикалык илимдин өнүгүүсү
Математика мектепте предмет катары Кыргызстанда Октябрь революциясынан кийин, жогорку математика болсо – Кыргызстанда биринчи ЖОЖ – Кыргыз мамлекеттик педагогикалык институту – азыркы Ж. Баласагын атындагы Кыргыз улуттук университети ачылгандан кийин окутула баштаган.
Кыргызстанда математика боюнча системалуу изилдөө иштери 1940-ыжлдан тартып семинарда профессор Г. А. Сухомлиновдун жетекчилиги астында жүргүзүлө баштаган. 1949-1965-жылдары семинарларды 1960-жылы Кыргыз ССРдин ИА мүчө-корреспонденти болгон профессор Я. В. Быков жетектеген, 1966-жылдан тартып бул семинарларды жалпыреспубликалык болуп, Институттун дубалында Кыргыз ССРдин ИА академиги (1979) жана СССРдин ИА (1981) мүчө-корреспонденти М. И. Аманалиев жетекчиликке алган.
1955-жылы Кыргыз ССРдин ИА Президиумунун астында, ал убакта эле илимдин кандидаттары Я. В. Быков жана М.И. Иманалиевдер курамында болушуп, Физика, математика жана механика бөлүмүн түзүшкөн.
1960-жылы Бөлүм Физика, матеатика жана механика Институту болуп өзгөртүлгөн. 1962-жылы ал Физика жана математика Институту аталып, 1984-жылы Физика жана математика Институтунун базасынын математикалык лабораториясынын базасында Математика институту уюштурулган. 2008-жылы анын базасында Теориялык жана прикладдык математика институту түзүлүп, а 2017-жылы ал КР УИА Математика институту болуп кайра аталган.
1984-жылдан 2016-жылга чейин Институтту М. И. Иманалиев жетектеген, а 2016-жылдан тартып бүгүнкү күнгө чейин академик А. А. Бөрүбаев жетектеп келет. Институттун негизги ишмердүүлүгү төмөнкү илимий изилдөөчүлүк багыттарды аныктайт:
- Тең калыптагы жана топологиялык тегиздиктер жана алардын чагылдырылышы.
- Функционалдык мейкиндик.
- Айырмасын, дифференциялдык жана интегро-дифференциялдык теңдемелерди түшүндүргөн, анын ичинде сингулярдык-кыжырдануучу динамикалык систкемалары.
- Интегралдык теңдемелер, корректүү эмес жана текери маселелер.
- Оптимизацияланган экономикалык маселелер.
Илимий изилдөөлөрдү компьютерлештирүү, объектилерди интерактивдүү таануу.
Изилдөө иштеринде көбүнчө теория жана интегро-дифференцирленген тиркемелерге, интегралдык жана дифференциалдык теңдемелерге, операциялык изилдөөлөргө, айырмачылык жана суммардык-айырмачылык теңдемелерге, математикалык физикага, сызыктуу алгебрага. Кыргызстандын математикадагы көпчүлүк ийгиликтери интегро-дифференциялдык теңдемелер чөйрөсүндө жетишилген. Математик окуумуштуулар математикалык илимге билимдүү, жогоркуинтеллектуалдуу, максатка умтулган жаш адистер келип Кыргызстанды мындан дагы жогорку бийиктиктерге жетишүүгө зор салымын кошооруна ишенишет.
Теңдемелер. Теңдемелердин тамыры
Өзгөрүлмөлүү барабарык теңдеме деп аталат.
Теңдеменин берилишин туура барабардыкка айландырган өзгөрүлмөнүн ар бир маанисин тендеменин тамыры деп айтабыз. Теңдемени чыгаруу – бул анын баардык тамырларын табуу же алар жок экенин далилдөө. Теңдеме бир, эки, бир нече тамырлардын көптүгүнө ээ болушу мүмкүн же тамтакыр ээ эмес болушу да мүмкүн.
1-мисал. 5 + x = 15 теңдемеси x = 10 болгон гана учурда 5 + x = 15 туура барабардыкка айланган жападан жалгыз тамырга ээ.
2-мисал. (5 + x)(x - 6)=0 теңдемеси -5 жана 6 деген эки тамырга ээ.
3-мисал. 9 + x2 = 0 чыныгы сандардын көптүгүндө эч тамырга ээ эмес.
Сызыктуу теңдемелер
Бир х өзгөрүлмөлүү ax = b түрүн сызыктуу теңдеме деп атайбыз, мында a, b –чыныгы сандар; а өзгөрүлмөнүн коэффициенти, b – бош мүчөсү деп аталат.
Теңдеменин тең салмактуулугу
Бирдей тамырга ээ болгон тендемелерди тең күчтүү тендмелер деп атайбыз. Тамырга ээ болболгон теңдемелер да тең салмакттуу деп аталат.
4-мисал. x + 5 = 7 жана x - 8 = -6 тндемелери тең салмактуу деп аталышат, анткени экөөнүн тең тамырлары 2ге барабар.
5-мисал. 9 + x2 = 0 жана 3x2 + 27 = 0 эки теңдеменин тең тамырлары болбогондуктан тең салмакттуу болушат.
6-мисал. 9 - x2 = 0 жана x + 4 = 7 тең салмактуу болушпайт, анткени биринчисинин тамырлары -3 жана 3, ал эми экинчисиники бир гана 3 деген тамырга ээ.
Тендемени чыгаруу учурунда аны болушунча жөнөкөй тең күчтүү болгондой берилиштер менен алмаштырат. Ошондуктан, кандай өзгөртүү учурунда ал тндемеге тең салмактуу болоорун.
1-теорема. Эгерде теңдемеде кансыл бир кошулуучунун барабардыктын экинчи жагына белгнисин карама-каршы кылып өзгөртүү менен которсок, анда ал теңдемеге тең барабардык келип чыгат.
Мисалы, x2 + 4 = 2x теңдемесине x2 + 4 - 2x = 0 тендемеси тең күчтүү болот.
2-теорема. Эгерде барабардыктын эки жагына тең бирдей нолдөн айырмаланган санды кобөйтүп же бөлсөк, анда ага барабар болгон теңдемени алабыз.
Мисалы, (x-5)/4 =4x теңдемеси x-5=16x теңдемесине тең күчтүү. Анткени эки тарабына тең 4тү көбөйттүк.
Теңдемелердин чыгарылышын мисалдар аркылуу көрөлү.
Теңдемелер эмне үчүн керек
Эсептөөчү маселелер түз жана кыйыр түрүндө болот. Биринчисинин чыгарылышына маселенин шарты түрткү кылат, ал эми кыйыр түрүндөгү маселелердин шарты анын чыгарылышына кандай алып бараары белгисиз болот. Мындан арифметикалык аталыштагы чыгарылышты кыйыр түрүндөгү маселелердин чыгарууда чоң чыгармачылыкты талап кылат. Ар бир жаңы маселе жаңыча пландоого алып келет. Эсептөө процессин алып кетүү үчүн негизги предмети болгон алгебраны окуп үйрөнүүдө теңдеменин ыкмасы түзүлгөн. Ошондон улам, теңдемени эсептөө процессин кыймылдатуу керек. Теңдеме түзүлгөндөн соң, анын чыгарылышын атоматтык түрдө дароо алсак болот. Маселени чыгаруунун кыйынчылыгы ал теңдеменин түзүлүшүнө жараша келип чыгат.
Теңдемени түзүү – бул маселенин белгилүүлөрү менен анын чоңдуктарынын белгисиздери ортосундагы байланышты математикалык формада туюндуруу.
Теңдемелердин жардамы менен маселелерди чыгарууну карайлы.
1-маселе. Апасы уулунан эки эсеге улуу. Он жыл мурун ал баласынан үч эсе улуу болчу. Апасы канча жашта?
2-маселе. Үч кутучада 56 калем сап бар. Биринчи кутучадагы калем саптарэкинчисине караганда эки эсе, ал эми үчүнчүсүнө караганда 2,5 эсеге көп экендиги белгилүү. Ар бир кутучуда канчадан калем сап бар?
3-маселе. Дарыянын агыбы боюнча теплоход жолду 9 саатта сүзүп өтөт. Агымга каршы 11 саатта. Эгерде дарыянынагымынын ылдамдыгы 2 км/с болсо теплоходдун өзүнүн ылдамдыгын тапкыла.
Пайдалуу шилтемелер
Теңдемелерди чыгаруу ыкмалары же жолдору алгач жетишээлик деңгээлде татаал жана ар түрдүү мүнөөздүү болгон. Математиканын өнүгүү процессинде алар жетишээлик жөнөкөйлөштүрүлдү жана ар бир түрдөгү теңдемелер үчүн чыгаруунун бирдиктүү алгоримти пайда болду. Кененирээк төмөндө көрсө болот: [Электрондук ресурс] // novykrug YouTube, 2018. URL:https://www.youtube.com/watch?v=WpwOQHVB5s4 (кайрылуу датасы: 28. 04. 2018)
Математикалык модель – бул реалдуу жашоо кырдаалдарын (маселелерди) математикалык тилдин жардамы менен түшүндүрүү ыкмасы. Биздин этапта алгебраны окуп-үйрөнүүдөгү маселелерди чыгарууда математикалык моделдөөнү колдонобуз.: .:[Электрондук ресурс] // school-assistant.ru © 2016 URL: http://school-assistant.ru/?predmet=algebra&theme=matemat_model (кайрылуу датасы: 28. 04. 2018)
Сызыктуу теңдемени колдонуу биздин жашообузда абдан кеңири колдонулат. Алар көптөгөн эсептөөлөрдо, имараттарды курууда жана да спортто да колдонулат. Адам баласы сызыктуу тендемени байыртадан бери колдонуп келүүдө жана азыр да колдонуу деңгээли өсүүдө. Сызыктуу теңдеме өзүнө алгебралык теңдемени түшүндүрүп, көп мүчөлөрдүн толук даражалары бирге барабар болот. Бул теңдемелержи чыгаруунун көптөгөн ыкмалары бар. Бул теңдемелерди чыгарууда өзгормөнүн маанисин табуу зарыл.: [Электрондук ресурс] // © Pocket Teacher. https://pocketteacher.ru/linear-equations-2-ru (кайрылуу датасы: 28. 04. 2018)
Глоссарий
- Алгебра – бул ар түрдүү чоңдуктагы жана чыгарылыштагы теңдемелердин үстүнөн болгон амалдардын жана бул амаладарга тиешелүү касиеттерин үйрөтүүчү математиканын бөлүмү.
- Чыныгы сандар (латындан realis — чыныгы) – айлана чөйрөдөгү геометриялык жана физикалык чоңдуктарды ченөө зарылдыгынан келип чыккан, ошондой эле тамырдан чыгаруу, логарифманы эсептөө, алгебралык теңдемелерди чыгаруу, функцияларды изилдөө сыяктуу эсептөөлөрдү жүргүзүүгө арналган математикалык объект.
- Квадраттык теңдеме – бул ax2 + bx + c = 0 түрүндөгү теңдеме, мында a, b жана c — коэффициенттери каалагандай сандар, мында a ≠ 0.
Библиография
- Математическая модель. Правила http://school-assistant.ru/?predmet=algebra&theme=matemat_model
- Основные математические знаки и символы: [Электронный ресурс] // 2013-2018 «SYL.ru» URL: https://www.syl.ru/article/327248/osnovnyie-matematicheskie-znaki-i-simvolyi (дата обращения: 26. 04. 2018)
- Институт математики.:[Электронный ресурс] // 2016-2017 Национальная академия наук КР URL:http://naskr.kg/index.php/ru/struktura-nan-kr/nauchno-issledovatelskie-uchrezhdeniya/institut-matematiki (дата обращения: 28. 04. 2018)
- Линейное Уравнение - Решение С Помощью Онлайн Решателя:[Электронный ресурс] // © Pocket Teacher. https://pocketteacher.ru/linear-equations-2-ru (дата обращения: 28. 04. 2018)
- Развитие математической науки Кыргызстана:[Электронный ресурс] //2018 © Институт Математики URL: http://math.aknet.kg/home/science-develop.pdf
- В.А. Гусев, А.Г. Мордкович Математика. Справочные материалы М.: Просвещение, 1988.
- Федин С. Н. Математики тоже шутят. — 4-е изд. — М.: УРСС, 2012. — 216 с.
Кошуу жана кемитүү белгилерин немис математикалык мектебиндеги алгебраистер тарабынан ойлонуп табылган. Алар Иоганн Видмандын (Johannes Widmann) 1489-жылы чыгарылган “Арифметикасында” колдонушкан. Ага чейин кошуу p (plus) тамгасы менен белгиленген же et латын сөзү менен (“жана” союз), а кемитүү m (minus) тамгасы менен белгиленген. Видмандын плюс символу кошууну эле эмес “жана” союзун да өзгөрткөн. Бул белгилердин чыгып келиш таржымалы белгисиз, арийне ал мезгилде бул символдорду же белгилерди соода-сатык иштеринде пайда жана жоготууну белгилешкен экен. Бул эки символ көз ирмемде жарым кылым эски белгини колдонуп келген Италиядан башка Европанын бүт аймагына тез тарап кеткен.
Көбөйтүү белгисин 1631-жылы Уильям Отред (Англия) кыйгач кайчылаш белги түрүндө киргизген. Ага чейин М белгиси колдонулуп келген. XVII кылымдын аягында Лейбниц кайчылаш белгини х белгиси менен чаташтырбоо үчүн чекит менен алмаштырган; буга чейн мындай белги Региомонтанада (XV кылым) жана англия окумуштуусу Томас Хэрриотдо (1560—1621) кездешкен.
Бөлүү белгиси. Отред кыйгач сызыкчаны туура көргөн. Кош чекит менен Лейбниц белгилөө жүргүзгөн. Аларга чейин көпчүлүк учурда D тамгасын колдонушкан. Фибоначчиден баштап араб жазылмаларындагыдай бөлчөк сызууну колдонушкан. Англиядан жана АКШда XVII кылымдын орто ченинде Йоханн Ран жана Джон Пеллдер сунушташкан ÷ (обелюс) символу тараган.
Барабар белгисин (1510—1558) 1557-жылы Роберт Рекорд сунуштаган. Ал дүйнө жүзүндө жарыш түрүндө барабар узундукка ээ болгон башка бир да белги жок деген. Континенталдык Европада барабар белгисин Лейбнциц киргизген.
“Барабар эмес” белги алгач жолу Эйлерде кездешкен. Салыштыруу белгисин өзүнун өлөөр алдындагы 1631-жылы чыгарган жазылмасында көрсөткөндөй Томас Хэрриот киргизген. Ага чейин: чоң, кичине сөздөрү менен жазышкан. Катуу салыштыруу символун Джон Валлис сунуштаган. Алгач сызыкча салыштыруу белгисиненен жогору болуп, а анын астында азыркыдай болгон.
Математика – аны менен билимдин чокусуна чыгуу үчүн анын ар бир кадамын биринчисинен акыркысына чейин басып өтө турган бийик бурамалуу тепкич сыяктанат.
Америкалык математик, болочок университеттин аспиарты Джордж Бернард Данциг бир күнү сабакка кечип калып тактада жазылып турган көнүгүүнү үй тапшырма катары кабыл алган. Ал көнүгүү ага татаалдай көрүнгөн, бирок, бир нече күн өткөндөн кийин ал аны чыгарган. Көрсө, ал көп окумуштуулар анын үстүнөн бушайман болушкан статистикага тиешелүү “чыгарылбаган” эки маселени чыгарыптыр.
Математикалык амалкөйлүк (софизм) – далилдөөдө байкабаарлыктай жашырылган, жетишээрик чанда кездешкен катасы бар таң калаарлык ырастоо.
Мартин Гарднер
Ар кандай маселелерди талдоо жана чыгаруу менен ой жүгүртүүнү жана логиканы өнүктүрүүгө болот. Математикалык амалкөйлүк дал ушундай маселелерге тиешелүү. Бирок, математикада тыкандык маанилүү экендигин эстен чыгарбоо керек. Бир логикалык конструкциядан кийинкисине өтүүдөгү ар бир кадамды так даана ойлонуу менен текшеир өтүү зарылдыгы турат. Бир эле туура эмес өтүү жөн эле так эместикке эле эмес, а чоң катачылыкка алып келет.
Математикалык амалкөйлүүлүктүн үч түрүн бөлүп карасак болот::
1. Арифметикалык 2. Алгебралык 3. Геометриялык
1) «Бир сом жүз тыйынга барабар эмес»
Эгерде эки тарабы бирдей болгон сандык барабардыкка каалагандай санды көбөйтүп же нөлдөн айырмаланган санга бөлсөк, анда чыныгы сандык барабардык келип чыгат, б.а. эгер a=b, c=d, анда ac=bd.
Запишем два очевидным равенства:
1 сом =100 тыйын (1)
10 сом = 10 ∙ 100 тыйын (2)
Тиешелүү жактарын көбөйтүү менен төмөнкүгө ээ болобуз:
10 сом =100 000 тыйын (3)
Соңунда алынган санды 10го бөлүү менен төмөнкүнү алабыз
1 сом = 10 000 тыйын
Ушул мүнөздө, бир сом 100 тыйынга барабар эмес. Катасы кайда?
Бул амалкөйлүктө кетирилген ката аталган чоңдуктардагы амалдардын эрежесинин бузулушунда: чоңдуктар менен болгон баардык амалдар алардын өлчөмдөрү менен да жүргүзүлүнүшү керек болот.
Чындыгында, (1) менен (2) ни көбөйтүү менен (3) тү алабыз, а 10 бөлгөндөн кийинки барабардык 10 сом =100 000 тыйын, 1 сом = 10 000 тыйын берет. Бул амалкөйлүктүн жазуу шартына туура келет.
2) 4 = 5.
Далилдөө. а = 4 жана b = 5 эки санды алалы алардын жарым сууммасын төмөндөгүчө белгилейбиз с = (а+b)/2.
Анда а = 2с- b и 2с - а = b.
Бул барабардыктын ар бир мүчөсүн көбөйтүү менен төмөнкүгө ээ болобуз:
а2 - 2ас = b2 - 2 bс.
Эки тарабына тең с2 кошуу менен төмөнкү алынат:
а2 - 2ас + с2 = b2 - 2bс + с2,
же (а - с)2 = (b - с)2.
Демек, а – с = b - с, мындан а = 6, б.а. 4 = 5.
Бул амалкөйлүктө кетирилген ката: эгерде сандардын квадраты барабар болсо, анда сандардын өздөрү барабар болуусу абзел эмес, алар карама-каршы да болушу мүмкүн. а-с= b-с барабардыгы бул учурда туура эмес, б.а. а-с= b-с же а - с = с – b болушу керек эле.
3) «Ширенкенин талы телеграфтык мамычадан экиэсе узун».
Далилдөө.
Мейли а ширенкенин талынын узундугу болсун жана b – мамчанын усундугу. b жана a нын айырмасын c ден белгилейли.
b - a = c, b = a + c алабыз
Бөлүктөрү боюнча бул барабардыкты көбөйтүү менен: b2 - ab = ca + c2 алабыз.
Эки тарабынан тең bc кемитебиз. Жыйынтыгында: b2- ab - bc = ca + c2 - bc, же
b(b - a - c) = - c(b - a - c), мындан
b = - c, бирок c = b - a, ошондуктан b = a - b, или a = 2b.
Катачылыктын негизи болуп бул амалкөйлүктө: b(b-a-c)=-c(b-a-c) барабардыктын туюнтулушу (b - a - c = с - с = 0) 0 гө бөлгөндөгүсү.
Окуучу мектептин алдындагы дүкөнгө кирип калат. Текчеде 1 даанасы 30 сом турган калем сап жана 15 сомдон калем турган. Бала 1 калем алып чыга берээрде жолдон ойлонуп: “Мен сатуучуга 15 сом бердим, демек, сатып алганды кайра берсем, менин эсебимде 30 сом болуп калат”. Окуучу бала калем сап сатып ала алабы? Эмне үчүн?
Ответ
Жообу: Ала албайт.
Түшүндүрүү максатында анча чоң эмес тамаша келтиребиз.
Студент кафеден булочка буюртма берип, соңунда кайра ойлонуп, аябай ачка экенин сезип аны бир чыны кофеге алмаштырды. Ичип бүтүп ал төлөбөстөн эле чыгууга жөнөдү. Аркасынан сатуучу чуркап барды.
-Сиз кофени төлөбөдүңүз!
-Ооба туура айтасыз, мен булочканын ордуна албадым беле!
-Булкага дагы төлөнгөн эмессиңер!
-Туура, бирок мен аны жеген жокмун да!
2. Алдыңарда туура эмес барабардык7+4-4=0. Бир ширенкенин талын жылдыруу менен кантип туура болгондой өзгөртөбүз?
3. Кроссвордду чыгар
Тигинен
4. Эки катыштын барабардыгы.
5. Теңдеменин коэффициенттери жана алардын тамырлары ортосундагы байланышты орноткон француз математиги.
Туурасынан
1. Теңдемедеги өзгөрүлмөнүн маанилери.
2. Өзгөрүлмөну камтыган барабардык
3. ax=b түрүндөгү теңдеме
4. Теңдемедеги белгисиз сан.