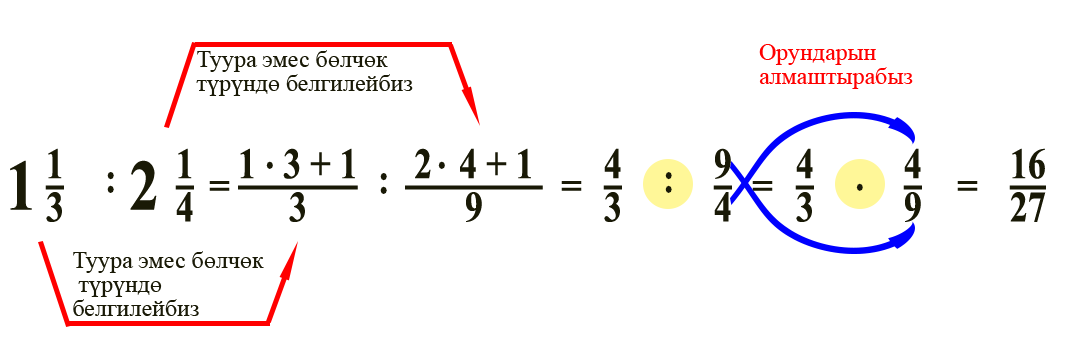Математика: Жөнөкөй бөлчөктөр менен амалдар
Бөлчөктөрдү топтоштурууга, алууга, көбөйтүүгө жана бөлүүгө болот. Бирок, кошуу жана алуу амалдары бөлүмүнөн көз каранды.
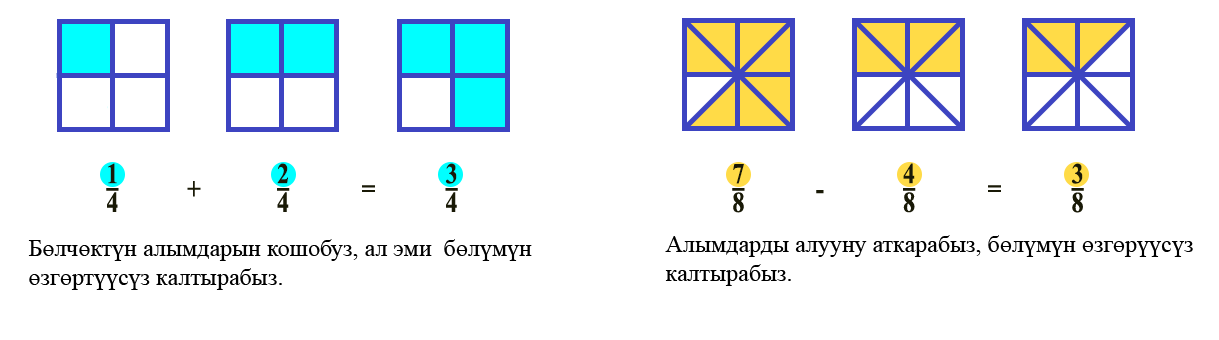
Бирдей бөлүмдүү жөнөкөй бөлчөктөрдү кошуу жана алуу
Бирдей бөлүмдүү жөнөкөй бөлчөктөрдү кошуу жана алуу үчүн алардын алымын кошуу же алуу жетиштүү.
Ар кандай бөлүмдүү жөнөкөй бөлчөктөрдү кошуу жана алуу
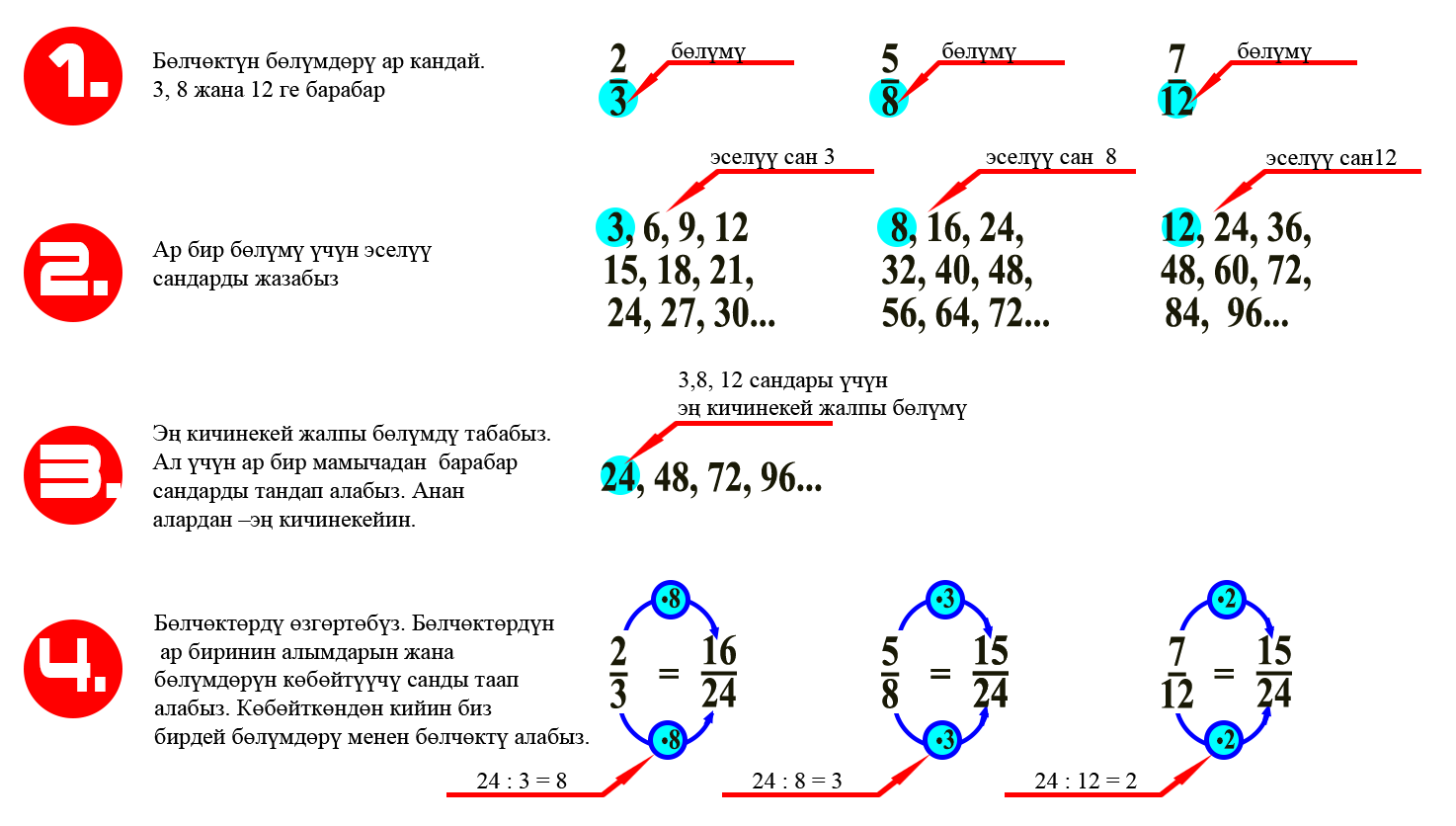
Ар кандай бөлүмдүү жөнөкөй бөлчөктөрдү кошуу жана алуу үчүн, аларды бир жалпы бөлүмүнө келтирип алабыз, андан соң кошуу алууну жогорку эреже менен эсептейбиз.
Жалпы бөлүмү деген эмне? Бөлчөктүн жалпы бөлүмү – бул ар бир берилген бөлүмгө бөлүнө турган сан.
Анда үч жөнөкөй бөлчөктү бир жалпы бөлүмгө келтиргенге аракет кылып көрөлү:
Азыр бизге жөнөкөй бөлчөктү жалпы бөлүмгө келтириш белгилүү болгондуктан мисалдарды чыгарып көрөлү:
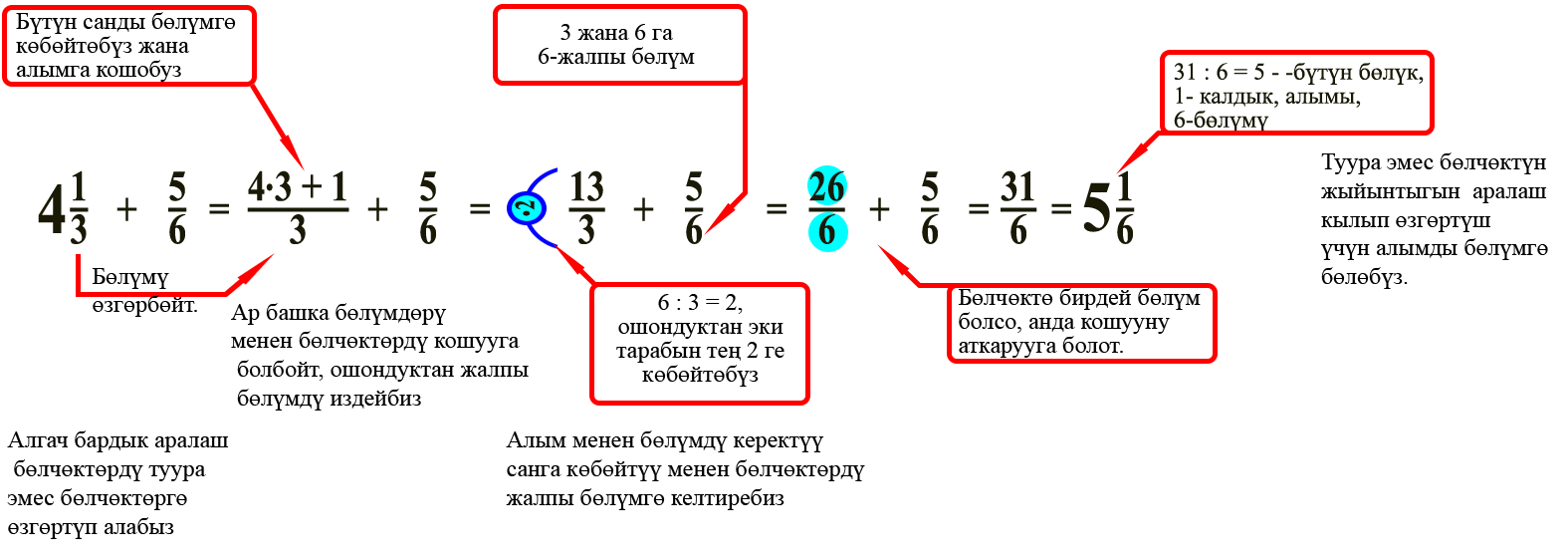
1-мисал. Бөлчөктөрдү кошууну аткаргыла.
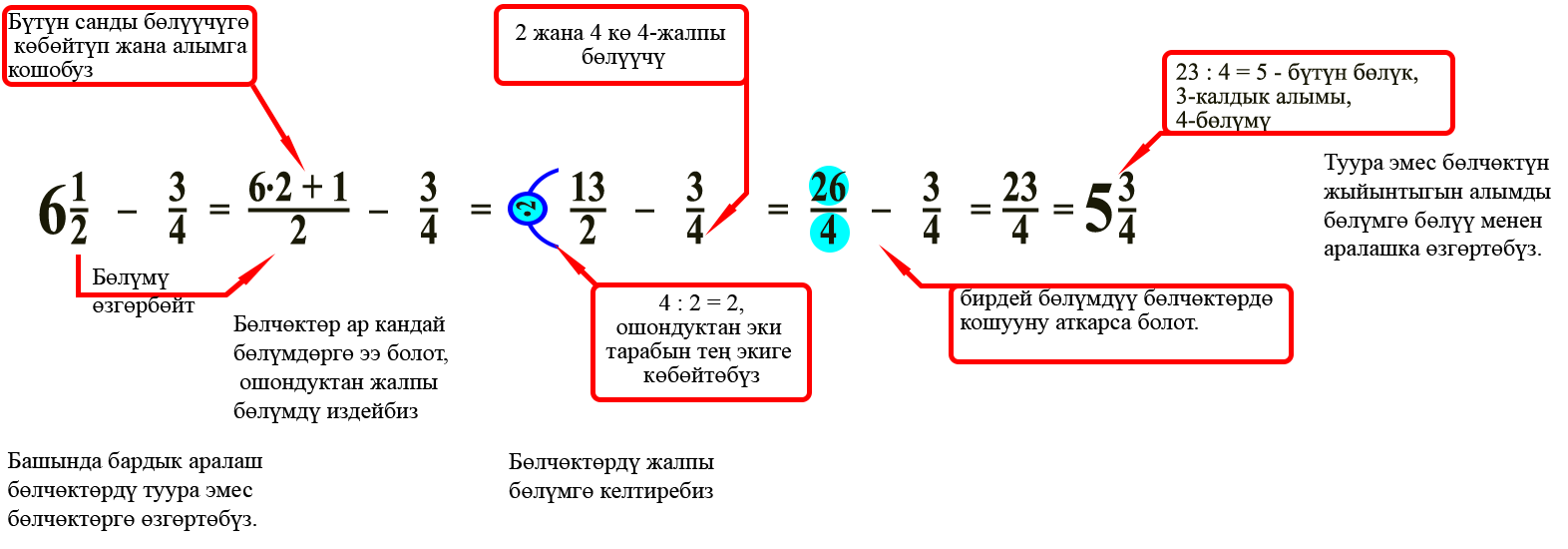
2-мисал. Бөлчөктөрдү алууну аткаргыла.
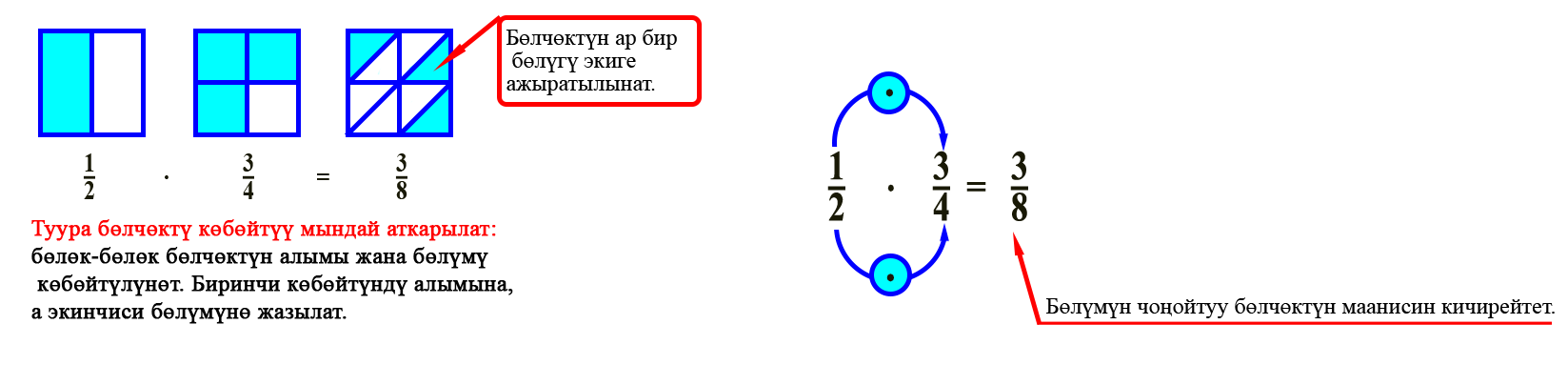
Бөлчөктөрдү көбөйтүү
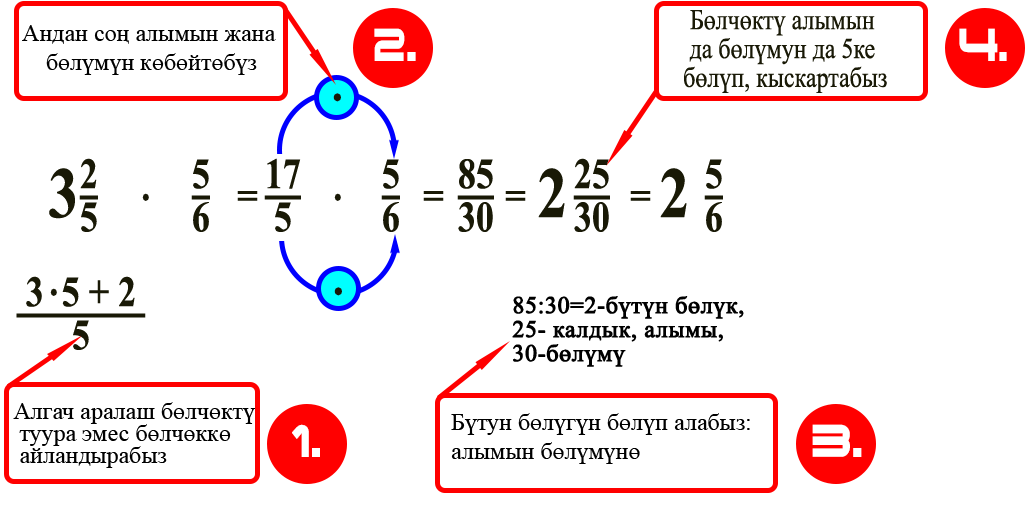
Аралаш бөлчөктү туура бөлчөккө көбөйтүш үчүн, биринчи аны туура эмес бөлчөккө айлантып алып анан жогорудагы эреже менен чыгаруу керек
Бөлчөктөрдү бөлүү
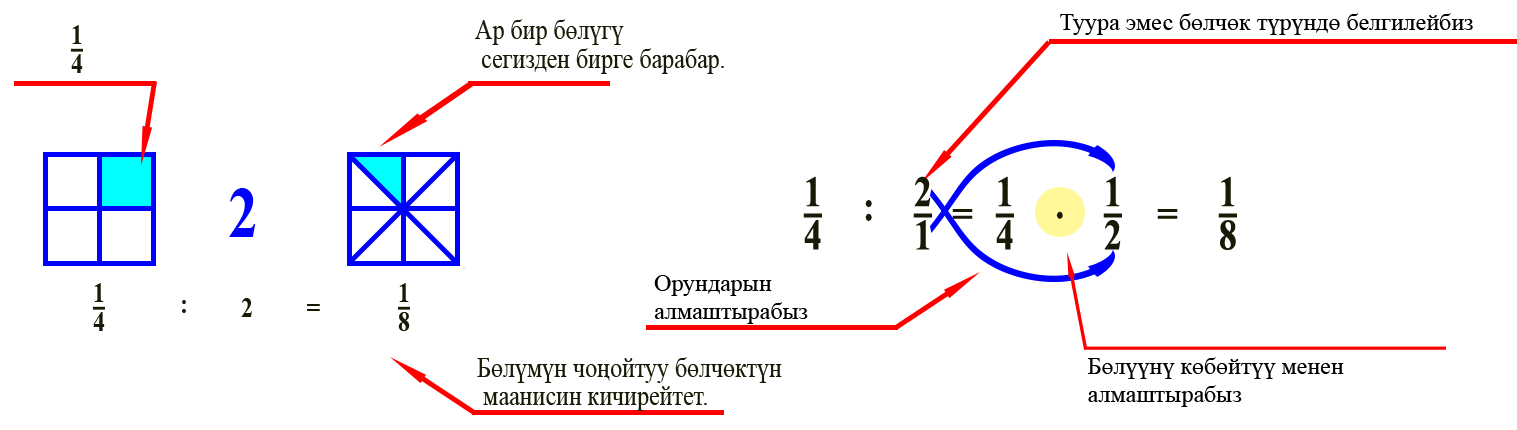
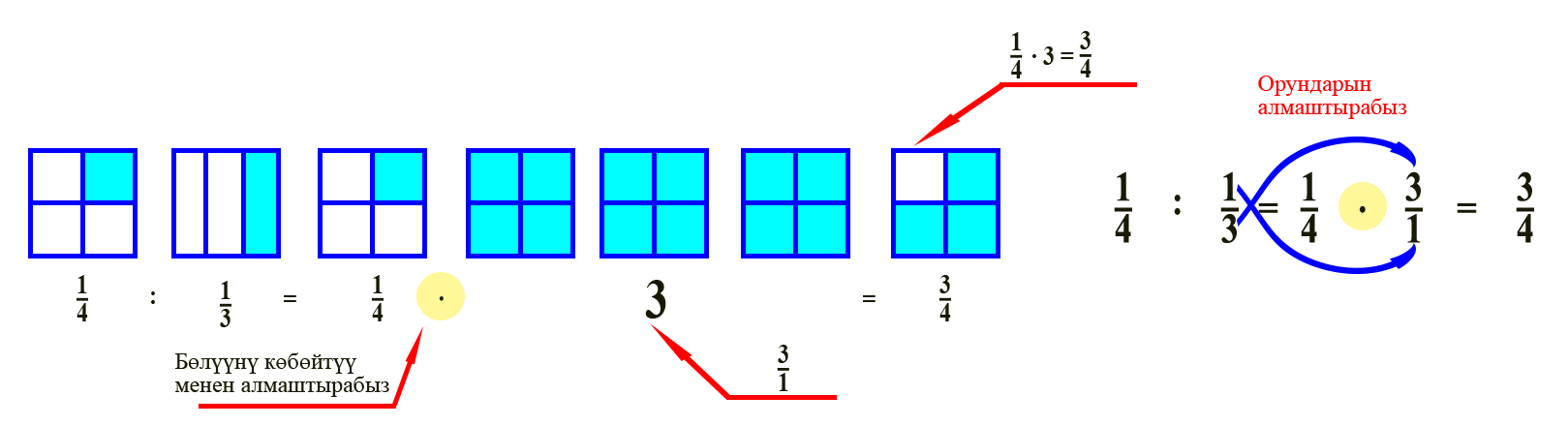
Бөлчөктөрдү бөлүүгө болот. Биринчи бүтүн сандардын бөлүнүшүн карап көрөлү. Бул үчүн бүтүн санды бөлчөктөй жазабыз, бөлүм менен алымдын оордуларын алмаштырабыз жана биринчи бөлчөккө көбөйтөбүз. Бул болсо бөлчөктүн бүтүн санга бөлүнүшүн бөлчөктү бирдей бөлүктөргө бөлүнгөндөй элестетет.
Туура бөлчөктү бөлүүгө өтөлү. Ал үчүн карама каршы амал– көбөйтүүнү колдонобуз.
Аралаш бөлчөктөрдү бөлүүдө биринчи аларды туура эмес бөлчөккө айлантып алабыз да андан кийин гана бөлүүнү жогорудагы эрежеге ылайык ишке ашырабыз.
Бөлчөккө карата эски маселелер
Байыркы кол жазмаларда, эски арифметикалык китептерде, керек болсо көркөм адабияттарда кызыктуу бөлчөккө маселелер абдан көп кездешет. Алардын чыгарылышы ой жүгүртүүнү, жөндөмдүүлүктү талап кылат. Алардын кээ бирин карап көрсөк болот.
Пайдалуу шилтемелер
Бөлчөктөр математикада каралып аткан чоңдуктун бөлүгүн белгилеш үчүн колдонулат. Эгерде сөз бөлүк жөнүндө болуп жаткан болсо, анда сөзсүз бүтүн да бар- анткени андан дал келчү бөлүк алынат да. Бүтүндү билүү менен анын бөлугүн таба билүү, көрсөтүлгөн дал келүүчү бөлчөк жана тескерисинче бүтүндүн белгилүү бөлүгү. Кененирээк: “Бүтүндүн бөлугүн жана бүтүндү анын бөлүктөрүнөн табууга маселелер” [Электрондук ресурс] //Marianna L YouTube, 2017. URL:https://www.youtube.com/watch?v=dLG5CXJtJlE . (кайрылуу датасы 20 ноября 2017)
Глоссарий
Арифметикалык прогрессия - Сандардын өсүшү, кийинки ар бир сан, экиден баштап мурунку туруктуу санды кошуу менен алынат.
Геометриялык прогрессия - сандардын өсүшү, ар бир кийинки сан, экиден баштап, мурунку санды аныкталган санга көбөйтүүдөн алынат.
Бөлчөк - бул бирдиктин бир же бир нече бөлүгүнөн турган сан.
Аралаш бөлчөк - бул бүтүн бөлүктүү бөлчөк.
Библиография
- Варга Б., Димень Ю., Лопариц Э. Тил, музыка, математика М.: Мир, 1981.-248 б.
- В.А.Гусев, А.Г.Мордкович Математика: сурамжылоо материалдары. Окуучулар үчүн китеп.-2-чыгарылыш-М.: Просвещение, 1990-416б
- Видеосабак “Бүтүндүн бөлугүн жана бүтүндү анын бөлүктөрүнөн табууга маселелер” [Электрондук ресурс]//Marianna L YouTube,2017. URL:https://www. youtube.com/ watch?v=dLG5CXJtJIE. (кайрылуу датасы 20.11.2017)
- Көпөлөктөр ыкмасы. Бөлчөктөрдү кошуу-алуу.: [Электрондук ресурс]//kid-mama,2017/URL:kid-mama/ru/metod-babochki-slozhenie-i-vychitanie-drobej/. (кайрылуу датасы 20.11.2017)
Эмне үчүн музыка көптөгөн кылымдар бою көбүнчө адамдар үчүн кызык? Эмне үчүн ал акылыбызды арбап, маанайыбызды ачып көңүлүбүздү көтөрөт же тескерисинче ойго салат?
Көрсө, музыкалык чыгармалар көзгө көрүнбөй турган бириге албаган нерселерди: Бийик мамилени жана математикалык эсепти бириктирет экен. Музыкада дагы математикадагыдай эсеп, жарыштык жана удаалаштык, пропорция жана симметрия бар. Ушулардын жардамы менен биз бийик жана жоон үндөрдү, тартылуу жана үзүк үндөрдү уга алабыз, үн тизмеги боюнча өйдө ылдый тепкич боюнча гаммаларды ырдайбыз.
Музыкада ар дайым санаш керек: 7 нота, 5 нота сызыгы, аралыктары бар. А ноталар баары ар кандай: бири кыска, башкалары узун. Музыканы жаздырууда үндөрдүн өздөрүнүн узундугу бар- ал узактыктыгы. Ушул жерден бөлчөктөрдүн жардамы менен жазыла турган бүтүн сандардын дал келиши жана бүтүн узактык, бөлчөк сандардын жана кыска ноталардын узактыгы жүрөт.
Музыкада биз кыска жана узун узактыктар менен иштешебиз, алар баардык ритмдерде: бүтүн нота, жарым, төрттүн биринде, сегиздин биринде, он алтынын биринде. Узактыктын аталыштары сандардын аталыштары менен бирдей кызматта. Эмне үчүн музыкалык ноталар аталыштарын бөлчөктөрдөн алганын түшүнүш кыйын эмес. Биз узактыктар бөлчөктөр сыяктуу эле бүтүн нотаны тең экиге бөлүү менен түзүлөөрүн көрө алабыз. Ошондуктан узактыкты бөлчөк сан катары карасак болот.
Барабардыкты бул жерде оң тараптын узактыгынын суммасы сол тараптын узактыгына барабар деген мааниде түшүнүш керек. Сандардын жардамы менен барабардыкты ар түрдүүчө жаза алабыз. Эгерде музыкалык чыгармалардагы баардык узактыкты эки эсеге көбөйтө алсак, анда чыгарманы жайыраак же тескерисинче аткара алабыз.
Кызык, узактыкты куруунун принциби геометриялык жана арифметикалык прогрессиянын курулуу принциптерине дал келет.
Байыркы Грецияда эле математика менен музыканы бир тууган дешкен, Пифагордун заманында музыка жөнүндө илимге пифагордук билим системасы арифметика (сандар жөнүндө илим) геометрия ( фигуралар жана алардын чени жөнүндөгү илим) жана астрономия (Ааламдын түзүлүшү жөнүндөгү илим) менен бирге кирген.
Монохорданын жардамы менен үндүн бийиктигин үйрөнүү менен – бир кылдан турган, резонатордук үкөктүн жана кыймылдагы коё турган, керилген кылдын узундугун өзгөртүүгө мүмкүн болгон. Пифагор таң калыштуу нерселерди тапкан. Жагымдуу угулган үн- кылдын узундугунан чыккан бул үндөр бүтүн төртөн бир санына дал келгенде гана консонансы болгону аныкталган, б.а. 1:2, 2:3, 3:4. Бул ачылыш Пифагорду таң калтырган: көрсө, үн менен үндөшүү жөнөкөй гана сандар менен жазылышы мүмкүн экен.
Пифагорчулар “алтын пропоцияны” ачышты-“алтын кесилиштин чекити”, музыкадагы анык аныкталган кульминациясынын оорду такталган.
Демокрит музыкалык аспаптара ойногондорду карап отуруп, андан чыккан үндүн тону кылдын узундугуна жараша өзгөрөөрүн билген. Ошонун негизинде ал музыкалык гамма жөнөкөй бүтүн сандарга карата тартылышы мүмкүн экенин аныктады.
Музыкалык изилдөөлөргө көптөгөн улуу математиктер өздөрүнүн иштерин арнаган алар: Рене Декарт (анын биринчи эмгеги –“Compendium Musicae” “Музыка жөнүндөгү трактат” деп которулат), Готфрид Лейбниц, Христиан Гольдбах, Жан Д Аламбер, Даниил Бернулли.
Композиторлор ыкмалары математикалык ыкмалардан бир аз эле айырмаланаарын көп айтышат. Ошол эле жөнүндө улуу дирижер Эрнест Ансерме: “ Математика менен музыканын ортосунда талапсыз жарыш бар. Ал дагы бул дагы ой жүгүртүү амалы, күнүмдүк жашоодогу ар кандай болуп кетчү нерселерден бизди куткаруучу” деп жазган. Көптөгөн улуу музыканттар математикалык өзгөчөлүк менен жарк этишкен: Азыр эле сөз кылган Эрнест Ансерме- кесипкөй математик жана Стравинскийдин эң мыкты аткаруучусу. Леонид Леонидович Сабанеев- Москвадагы Университеттин математика факультетинин бүтүрүүчүсү, эң мыкты пианист, композитор жана Скрябиндин досу. Улуу вианчелист Карл Юльевич Давыдов физика-математика факультетин бүтүргөн, аны өзүнүн замандаштары эскергендей “таза жана колдонмо математикага укмуштуудай жөндөмү болгон. Анын үйүндө өзүнүн жасаган темир жол көпүрөсүнүн модели көпкө сакталып турган. Ал кесиптештеринин сөзүндө көңүл бөлүүгө татыктуу дешкен.” </p>
Белгилүү музыканттардын жашоосундагы кызыктуу фатылар
Николай Андреевич Римский-Корсаков- орус композитору, педагог, дирижёр, коомдук ишмер, музыкалык сынчы- Санкт-Петербургдагы математика жана навигация мектебинде окуган. Мектептин директору Николай үчүн музыка сабагы анын уялчаактыгын жоёт деп эсептеген. Ал эми Римский-Корсаков музыкага болгон сүйүүсү оркестрлардын концертине жана операларга баргандан кийин ойгонгондугун жазган.
Альбер Шарль Поль Мари Руссель- ХХ кылымдын үчтүн бириндеги белгилүү француз композитору- 25 жашында музыка менен алектенип баштаган. Башында ал математикага кызыккан, француз флотунда 7 жыл мичман болгон. Кийин ал көпкө чейин Түштүк-Чыгыш Азияда кораблда кызмат кылган жана 25 жашында отставкага кеткен. Ошол кезден баштап ал музыкага чындап кызыгып баштаган. Тактап айтсак- гармонияны окуп үйрөнгөн.
Арам Ильич Хачатурян-советтик композитор, дирижёр, музыкалык-коомдук ишмер, педагог- 19 жашынан баштап музыка менен чындап алектенип баштаган. Хачатурян мектепте жүргөндө эле фортепианодо, горнеде жана тубеде ойногон, бирок ата-энеси бул кызыгуусун колдогон эмес. Мектептен кийин ал физикаматематикалык факультетке тапшырган. Бирок Арамдын чыдамы аз гана убакытка жеткен. Бир жылдан кийин ал Гнесин музыкалык окуу жайынына тапшырып виолончели менен фортепианодон компазициялардын сабаган алган.
Брайн Мэй- гитарист “Queen”- Лондондогу белгилүү Империя колледжинин физико-математикалык факультетин бүтүргөн. Брайындын инфра кызыл диапозондогу астрономиялык изилдөөлөрү боюнча философия илимдеринин доктору даражасына диссертациясы даяр болгон жана астрономия боюнча эки илимий чыгарылышы (публикациясы) бар эле.
“Queen”дин ийгилиги - аны илимий карьерасын токтоткон. Бирок кийин ал изилдөө кызматына кайтып келип баштаган ишин аягына чыгарып, Хертфордширск университетинде даражасын алган. 14 апрель 2008 жылы музыкант Джон Мурс атындагы Ливерпуль университетинин ректору болуп дайындалып бул кызматта 2013 жылдын мартына чейин турган. Азыркы учурда Брайан “Queen”- группасында музыкалык карьерасын жана теоретикалык физика математика тармагындагы илимий иштерин да улантууда.
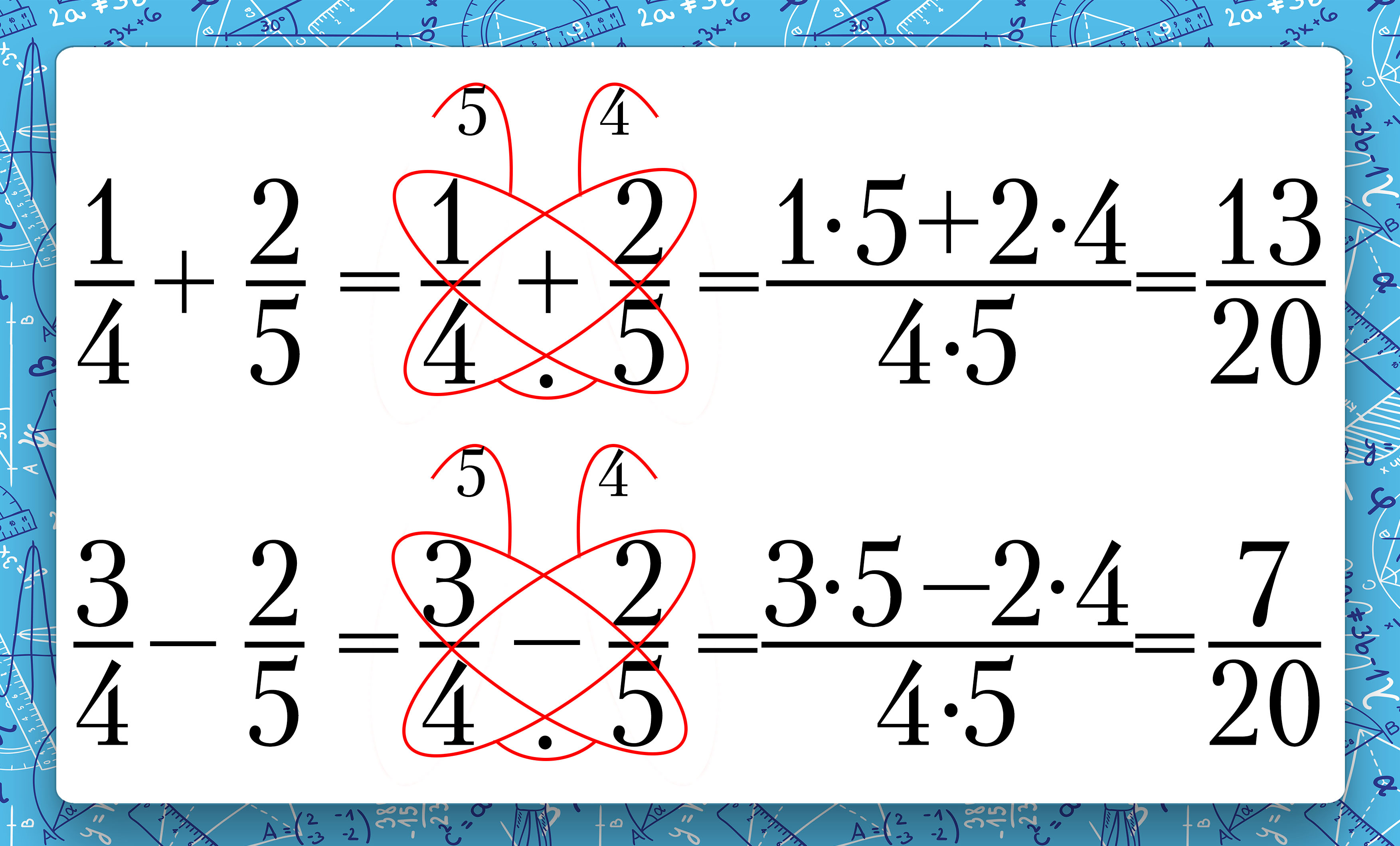
Аныкталган математикалык мыйзам ченемдүүлүктө көптөгөн трюктар ойлонулган санды табуу менен куралат. Бирок бул мыйзам ченемдүүлүктөрдү жалаң ган тамаша табышмактарга пайдаланбай, а чындыгында тез эсептеш керек болгон, бирок жардам бере калчу колдо эч кандай гаджет жок абалга жардамга даяр. Анда, силердин алдыңарда “Көпөлөктүн ыкмасы”: ар башка бөлүмдүү жөнөкөй бөлчөктөрдү бат кошуп- алуу.