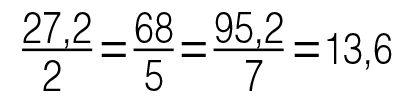Математика: Катыш жана пропорция
Пропорция жөнүндө окуп-үйрөнүүнүн өнүгүү тарыхы
Сулуулуктан бөлөк эч нерсе жакпайт, а сулуулукта- эч нерсе, формадан бөлөк, формада- эч нерсе,
пропорциядан бөлөк, пропорцияда эч нерсе, сандардан бөлөк.
Аврелий Августин
Кесиндини четки жана ортоңку катышынан кесүүдө келип чыккан пропорцияга карата алгачкы кызыгуулар антикалык илимдерде эле пайда болгон .
Байыркы Грецияда даңталган чыгармачылык искусствосунун, архитектурасынын, ар кандай кол өнөрчүлүктөрдүн доорунда өзгөчө ийгиликтүү өнүккөн. Пропорция менен сулуулукту даңазалоо, тартип жана гармония, музыкадагы үн коштоочу аккорддорду байланыштырышкан. Алтын бөлүнүш жөнүндө түшүнүгүн колдонууну байыркыгрек философу жана математиги Пифагор киргизген. Ал жана анын окуучулары пропорциянын үч түрүн карашкан:
- Арифметикалык: а - b = с - d
- Геометрикалык: a : b = c : d
- Гармоникалык: a : b = b : (a - b)
Башка байыркы грек окумуштуусу Платон пропорциянын маңызын мында: «эки жакты үчүнчү менен бириктирүү, аларды бир бүтүнгө «бекемдөө» үчүн пропорция керек. Мында бүтүндүн бир бөлүгү башкага бүтүндүн чоң бөлүгүнө мамиле кылгандай болуу керек. Мындай пропорция гармониялык биригүүгө жооп берет жана ал алтын болуп саналат».
Байыркы грек окумуштуусу Евдокс бүтүн сандарга гана эмес ошондой эле бөлчөк сандарга дагы колдонула турган пропорция жөнүндөгү систематикалык окууну берген. Катуу талаптуу пропорциянын теориясы биздин кылымга чейинки 3 кылымда байыркы грек геометриги Евклиддин белгилүү «Башталышында» берилген, ал 13 китептен турган. Бул теорияга ал 5 китепти арнаган. Евклид өзүнүн теориясынын негизин Евдокстун окууларынан алган. Азыркы убакта пропорциянын теориясы Евдокс – Евклиддин теорияларынан аз эле айырмаланат. Евклид пропорциялар арасындагы салыштырууну аныктаган: a : b катышы, c : d катышынан кичине, эгерде m жана n сандары болсо, эгерде ma > nb жана ошол эле убакта mc ≤ nd. А бул мындайча окулат: Бул факт таң калаарлык, анда «пропорция» сөзүн пайдаланууга байыркы рим коомдук ишмери МаркТу́ллийЦицеро́н киргизген.
Ал латынчага платон термини «аналогия» ны которгон, ал сөзмө-сөз «кайрадан -мамиле» дегенди билдирген, же биз азыр айтып жаткандай «катыш».
Негизги түшүнүктөр
Пропорция (лат. proportio — соразмерность, выровненность частей) – это равенство двух отношений: ![]() или a:b=c:d, где a,b,c,d – не равны нулю, a и d называют крайними членами пропорции, b и c – средними членами пропорции.}}
или a:b=c:d, где a,b,c,d – не равны нулю, a и d называют крайними членами пропорции, b и c – средними членами пропорции.}}
Например, рассмотрим равенство 12 : 20 = 3 : 5.
Бул пропорция, акыркы мүчөлөрү 12 жана 5 ке барабар, ортоңку мүчөлөрү 20 жана 3. Пропорция мындайча окулат: он эки жыйырмага карайт, үч бешке карагандай.
Пропорциянын негизги касиеттери: пропорциянын акыркы мүчөлөрүнүн көбөйтүндүсү анын ортоңку мүчөлөрүнүн көбөйтүндүсүнө барабар.
Бул болсо,эгерде ![]() , анда ad = bc.
, анда ad = bc.
Карама-каршы ырастоо дагы туура: эгерде эки сандын көбөйтүндүсү a жана d эки башка сандын көбөйтүндүсүнө барабар болсо b жана c (a≠0,b≠0,c≠0,d≠0), анда бул сандар менен ![]() пропорциясын түзсөк болот.
пропорциясын түзсөк болот.
Пропорцияга мисалдар жана тапшырмалар
1-тапшырма Пропорциянын белгисиз мүчөсүн тапкыла.
2-тапшырма Китепканадагы 300 окурмандын 108 и- студенттер. Бардык окурмандардын канча процентин студенттер түзөт?
3-тапшырма Кыям кайнатууда жемиш менен кумшекер 5:2 катышта колдонулат. Эгерде 450 грамм кумшекер алсак канча жемиш керек болот?
Түз жана кыйыр пропорционалдуулук
Пример. Масса любого вещества пропорциональна его объёму. Например, 2 литра ртути весят 27.2 кг, 5 литров весят 68 кг, 7 литров весят 95.2 кг. Отношение массы ртути к её объёму (коэффициент пропорциональности) будет равно:
Таким образом, коэффициентом пропорциональности в данном примере является плотность.
Пропорциональность. Это простейший вид функциональной зависимости. Различают прямую пропорциональность. (y=kx) и обратную пропорциональность (y=k/x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S=vt ; прямо пропорциональна величина основания y прямоугольника с заданной площадью a обратно пропорциональна высоте x, т. е. y=a/x.
Свойства прямой пропорциональной зависимости.
1. Каждому значению х соответствует единственное определенное значение у. (первое свойство прямой пропорциональной зависимости)
2. Отношение соответствующих значений величин у и х, связанных прямой пропорциональностью, равно коэффициенту пропорциональности.
3. Если две величины связаны между собой прямой пропорциональной зависимостью, то при увеличении (уменьшении) одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз.
Математической моделью прямой пропорциональной зависимости величин х и у является формула у = кх.
Свойства обратной пропорциональной зависимости.
1. Каждому значению х (за исключением х=0) соответствует вполне определенное значение у.
2. Произведение соответствующих значений х и у равно коэффициенту обратной пропорциональности.
3. Если х увеличивается (уменьшается) в несколько раз, то у уменьшается (увеличивается) во столько же раз, так как их произведение остается неизменным.
Если х и у связаны обратной пропорциональной зависимостью, то отношение двух любых значений величины х равно обратному отношению соответствующих значений y: x1:x2=y2:y1.
Маселени чыгаруу
1-маселе Велосипедист туруктуу ылдамдык менен 10 минутада 5 км басып өткөн. 45 минутада канча жол басып өтөт?
2-маселе Автомашина 2 саатта ылдамдыгы 75 км/саат жүргөн. Эгерде ал ушул эле убакытта ылдамдыгы 90км/саат жүрсө канча аралыкты басып өтөт?
Алтын кесилиш
Геометрия эки кенге ээ: анын бири- Пифагордун теоремасы,
экинчиси-кесиндилерди ортоңку жана акыркы катыштарга бөлүү...
Биринчисин алтындын өлчөмү менен салыштырууга болот, а экинчиси баалуу ташка окшош.
Иоганн Кеплер
Түз кесиндини эки барабар бөлүккө, ошондой эле эки барабар эмес бөлүккө каалагандай катышта бөлүүгө болот. Акыркысын алтын бөлүү десек болот же кесиндини акыркы жана ортоңку катышта бөлүү.
Алтын кесилиш - бул кесиндини барабар эмес бөлүктөргө пропорционалдуу бөлүү, мында бүт кесинди чоң бөлүккө карайт, ал эми чоң бөлүктүн өзү кичинекейге карайт; же башкача айтканда, кичинекей кесинди ушундай эле чоңго карайт, чоң бардыгына карагандай: a : b = b : c же с : b = b : а.
Алтын кесилиш менен практика жүзүндө таанышууну кесиндини түз алтын пропорцияда циркулдун жана сызгычтын жардамы менен бөлүүдөн башташат.
Алтын пропорциянын кесиндилери чексиз ирроционалдык бөлчөктөр менен туюнтулат AE = 0,618..., эгерде AB бирдик деп кабыл алсак, BE = 0,382...
Практикалык максатта көбүнчө жакындатылган мани 0,62 жана 0,38 ди пайдаланышат. Эгерде АВ кесиндисин 100 бөлүк деп кабыл алса, анда кесиндинин чоң бөлүгү 0,62 ге барабар, а кичинекей бөлүгү -38 бөлүккө. Алтын кесилиштин касиетин бул сандын айланасында түзүшкөн романтикалык сырдуулуктун ореолу жана араң эле мистикалык таазим этүү эмес.
Пифагор алтын бөлүү билимин египеттиктер менен вавилондуктардан алган деген божомол бар. Чындыгында эле Хеопс пирамидасы, храмдар, барельефтери, турмуштагы предметтер жана Тутанхамон көрүстөнүндөгү жасалгалар египеттик чеберлердин аларды түзүүдө алтын кесилиш катышын пайдалангандары күбө болуп турат. Француз архитектору Шарль Эдуард Ле Корбюзье Абидостогу Сети I фараонунун ибадатканасынын рельефинен жана Рамзес фараонунун сүрөттөлүшүндө фигуралардын пропорциясы алтын бөлүү чоңдугуна дал келээрин тапкан. Хесира көрүстөнүндөгү жыгач тактага түзүрүлгөн Зодчийдин рельефинде, колунда алтын бөлүү пропорциясын бекитүүчү ченөө инструменттерин кармап турат. Гректер акылдуу геометрлар болушкан. Алар балдарына арифметиканы дагы геометриялык фигуралардын жардамы менен окутушкан. Пифагордун квадраты жана ал квадраттын диагоналы динамикалык тик бурчтукту түзүү үчүн негиз болгон.
Байыркы грек Парфенон храмынын фасадында алтын пропорция бар. Аны касууда байыркы (античный) дүйнөнүн архитекторлору жана скульпторлору пайдаланган циркульдар табылган. Помпеядагы колдонулган циркульга дагы алтын бөлүү пропорциясы мүнөздүү. Алтын кесилиш терминин Леонардо да Винчи (1452-1519-жж) киргизген.
Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.
Алтын кесилиштин пропорциясына геометриялык фигура негизделет. Жактарынын ушундай катыштагы тик бурчтугу алтын тик бурчтук деген аталышка ээ болгон. Разумеется есть и золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618.
Бизди курчаган пропорциялар
Скрипканын добушу, анын үнүнүн сулуулугу кайсы бир өлчөмдө инструменттин формасынын алтын кесилиш пропорциясы менен келишиминен түз көз каранды. Музыкалык чыгармалардын Бахадан Шостаковичке чейинки диапозонунун анализи музыкалык формалардын негизги метрдик катыштарын жана ошондой эле алтын кесилишти көрсөткөн. Ошентип, гармония закону музыкалык тизмекте, Менделеевдин таблицасында, планеталар ортосундагы аралыкта, микро- жана макрокосмосто, илимдин көптөгөн тармактарында табылган. Скульптура, архитектура, астрономия, биология, техника, психология, ж.б.- бардык жактарда алтын кесилиш өзүн көрсөтүүдө.
Полезные ссылки
- Видеоурок на тему «Прямая и обратная пропорциональные зависимости» [Электронный ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html (дата обращения: 24. 04. 2018)
- Видеоурок на тему «Пропорции»: [Электронный ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Proportsii.html (дата обращения: 24. 04. 2018)
- Теория пропорций: [Электронный ресурс] // 2006-2018 ФГАУ ГНИИ ИТТ "Информика" URL: http://files.school-collection.edu.ru/dlrstore/c4d6841c-5a1e-ab8e-3524-e712079e89f0/00145619554921908.htm (дата обращения: 24. 04. 2018)
Глоссарий
Отношение – это частное от деления одного числа на другое.
Пропорция – это равенство двух отношений.
Чи́сла Фибона́ччи — элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …, в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел.
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ, в честь древнегреческого скульптора и архитектора Фидия.Число Φ называется также золотым числом.
Библиография
- Белянин В.С. Владел ли Платон кодом золотой пропорции? Анализ мифа.: [Электронный ресурс] // Академия Тринитаризма URL: http://www.trinitas.ru/rus/doc/0016/001b/00161296.htm (дата обращения: 24. 04. 2018)
- Золотое сечение: [Электронный ресурс] // МОО «Наука и техника», 1997...2018 URL: http://n-t.ru/tp/iz/zs (дата обращения: 25. 04. 2018)
- Золотое сечение в дизайне сайтов: [Электронный ресурс] // 2016 UX Guide URL: http://uxguide.ru/dizajn/zolotoe-sechenie-v-dizajne-sajtov/ (дата обращения: 25. 04. 2018)
- Золотое сечение: [Электронный ресурс] // Блог Рунмастера | © 2006-2018 URL: http://rustimes.com/blog/post_1177437753.html (дата обращения: 25. 04. 2018)
- А. С. Пушкин. Сапожник. Притча: [Электронный ресурс] //Электронная публикация — РВБ, 2000—2018 URL: http://rvb.ru/pushkin/01text/01versus/0423_36/1829/0521.htm (дата обращения: 25. 04. 2018)
- 15 примеров золотого сечения в архитектуре. Jelena Shiljajeva M.A. in History of Art, University of Glasgow: [Электронный ресурс] //URL: https://arhi1.ru/ob-arhitekture/nauka/zolotoe-sechenie (дата обращения: 25. 04. 2018)
- Ле Корбюзье: [Электронный ресурс] //ArchAndArch.ru 2010-2018 URL: http://www.archandarch.ru/архитекторы/ле-корбюзье/ (дата обращения: 25. 04. 2018)
- Видеоурок на тему «Прямая и обратная пропорциональные зависимости» [Электронный ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html (дата обращения: 24. 04. 2018)
- Видеоурок на тему «Пропорции»: [Электронный ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Proportsii.html (дата обращения: 24. 04. 2018)
- Теория пропорций: [Электронный ресурс] // 2006-2018 ФГАУ ГНИИ ИТТ "Информика" URL: http://files.school-collection.edu.ru/dlrstore/c4d6841c-5a1e-ab8e-3524-e712079e89f0/00145619554921908.htm (дата обращения: 24. 04. 2018)
Правильное распределение энергий внутри дома, гармоничные конструкции в сочетании с экологией и безопасностью строительных материалов побуждают современных архитекторов и дизайнеров использовать принципы и понятия «Золотого сечения». Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.
Для талантливых художников и архитекторов правило сохраняется интуитивно во время творческого процесса. Однако некоторые из них сознательно реализуют это положение.
Известный французский архитектор Шарль Эдуард Ле Корбюзье для расчёта параметров будущего дома и интерьера использовал в качестве отправной единицы рост хозяина. Все его работы по-настоящему индивидуальны и гармоничны.
В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали. Для этого достаточно переставить мебель или сделать дополнительную перегородку. Аналогичным образом меняется высота и длина окон и дверей.
В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.
Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.
Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.
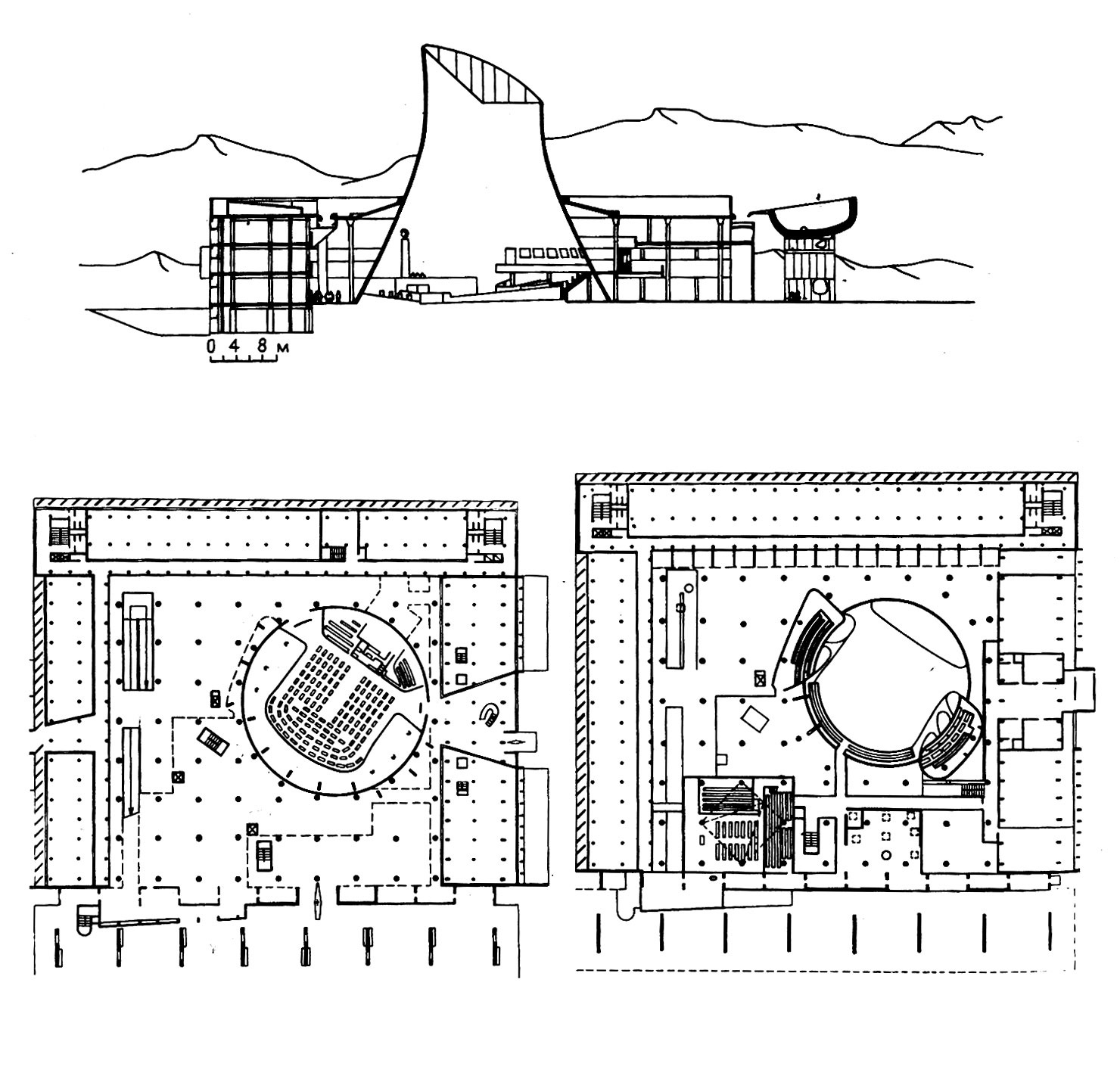
Архитектурные комплексы, которые расположены на территории Кыргызстана, занимают значительное место в истории зодчества народов Центральной Азии, соединив в себе лучшие достижения в области строительной техники, архитектуры и декоративного оформления своего времени.
Пропорциянын эң башкы эрежеси
Баардыгы билип эстеп калуу керек
Ортоңку мүчөлөрүн четкилерине көбөйтсөк
Бул мүчөлөрү дайыма тең болот.