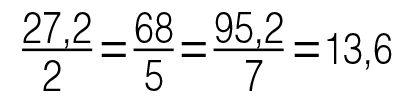Математика: Катыш жана пропорция
Версия от 14:37, 21 мая 2018; Msu05 (обсуждение | вклад) (→Пропорция жөнүндө окуп-үйрөнүүнүн өнүгүү тарыхы)
Пропорция жөнүндө окуп-үйрөнүүнүн өнүгүү тарыхы
Сулуулуктан бөлөк эч нерсе жакпайт, а сулуулукта- эч нерсе, формадан бөлөк, формада- эч нерсе,
пропорциядан бөлөк, пропорцияда эч нерсе, сандардан бөлөк.
Аврелий Августин
Кесиндини четки жана ортоңку катышынан кесүүдө келип чыккан пропорцияга карата алгачкы кызыгуулар антикалык илимдерде эле пайда болгон .
Байыркы Грецияда даңталган чыгармачылык искусствосунун, архитектурасынын, ар кандай кол өнөрчүлүктөрдүн доорунда өзгөчө ийгиликтүү өнүккөн. Пропорция менен сулуулукту даңазалоо, тартип жана гармония, музыкадагы үн коштоочу аккорддорду байланыштырышкан. Алтын бөлүнүш жөнүндө түшүнүгүн колдонууну байыркыгрек философу жана математиги Пифагор киргизген. Он и его ученики рассматривали три вида пропорций:
- Арифметическую: а - b = с - d
- Геометрическую: a : b = c : d
- Гармоническую: a : b = b : (a - b)
Другой древнегреческий ученый Платон сводил сущность пропорции к тому, что «для соединения двух частей с третьей совершенным образом необходима пропорция, которая бы «скрепила» их в единое целое. При этом одна часть целого должна так относиться к другой, как целое к большей части. Такая пропорция отвечает гармоническому соединению, она и является золотой».
А древнегреческий ученый Евдокс дал систематическое учение о пропорциях применительно не только к целым, но и к дробным числам. Строгая теория пропорций была построена в 3 веке до н.э. древнегреческим геометром Евклидом в его знаменитых «Началах», состоящих из 13 книг. Этой теории он посвящает 5 книг. В основу своей теории Евклид положил учение Евдокса. В настоящее время теория пропорций мало отличается от теории Евдокса – Евклида. Евклид определяет сравнение между пропорциями: отношение a : b меньше, чем отношение c : d, если есть такие числа m и n, если ma > nb и в то же время mc ≤ nd. А читается она так: «В верной пропорции произведение крайних членов равно произведению средних». Математические свойства пропорции уже тогда создавали вокруг нее ореол таинственности и мистического поклонения. Удивителен тот факт, что слово «пропорция» ввел в употребление древнеримский политический деятель Марк Ту́ллий Цицеро́н.
Он перевел на латынь платоновский термин «аналогия», который буквально означал «вновь-отношение», или, как мы говорим, «соотношение».
Основные понятия
Пропорция (лат. proportio — соразмерность, выровненность частей) – это равенство двух отношений: ![]() или a:b=c:d, где a,b,c,d – не равны нулю, a и d называют крайними членами пропорции, b и c – средними членами пропорции.}}
или a:b=c:d, где a,b,c,d – не равны нулю, a и d называют крайними членами пропорции, b и c – средними членами пропорции.}}
Например, рассмотрим равенство 12 : 20 = 3 : 5.
Это пропорция, в которой крайние члены равны 12 и 5, а средними членами являются числа 20 и 3. Читается пропорция так: двенадцать относится к двадцати, как три относится к пяти.
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Это означает, что если ![]() , то ad = bc.
, то ad = bc.
Верно и обратное утверждение: если произведение двух чисел a и d равно произведению двух других чисел b и c (a≠0,b≠0,c≠0,d≠0), то из этих чисел можно составить пропорцию ![]() .
.
Задачи и задания на пропорции
Задание 1. Найдите неизвестный член пропорции.
Задание 2. Из 300 читателей библиотеки 108 человек – студенты. Какой процент всех читателей составляют студенты?
Задание 3. При варке варенья используют ягоды и сахар в отношении 5:2. Сколько надо ягод, если взяли 450 грамм сахара?
Прямая и обратная пропорциональность
Пример. Масса любого вещества пропорциональна его объёму. Например, 2 литра ртути весят 27.2 кг, 5 литров весят 68 кг, 7 литров весят 95.2 кг. Отношение массы ртути к её объёму (коэффициент пропорциональности) будет равно:
Таким образом, коэффициентом пропорциональности в данном примере является плотность.
Пропорциональность. Это простейший вид функциональной зависимости. Различают прямую пропорциональность. (y=kx) и обратную пропорциональность (y=k/x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S=vt ; прямо пропорциональна величина основания y прямоугольника с заданной площадью a обратно пропорциональна высоте x, т. е. y=a/x.
Свойства прямой пропорциональной зависимости.
1. Каждому значению х соответствует единственное определенное значение у. (первое свойство прямой пропорциональной зависимости)
2. Отношение соответствующих значений величин у и х, связанных прямой пропорциональностью, равно коэффициенту пропорциональности.
3. Если две величины связаны между собой прямой пропорциональной зависимостью, то при увеличении (уменьшении) одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз.
Математической моделью прямой пропорциональной зависимости величин х и у является формула у = кх.
Свойства обратной пропорциональной зависимости.
1. Каждому значению х (за исключением х=0) соответствует вполне определенное значение у.
2. Произведение соответствующих значений х и у равно коэффициенту обратной пропорциональности.
3. Если х увеличивается (уменьшается) в несколько раз, то у уменьшается (увеличивается) во столько же раз, так как их произведение остается неизменным.
Если х и у связаны обратной пропорциональной зависимостью, то отношение двух любых значений величины х равно обратному отношению соответствующих значений y: x1:x2=y2:y1.
Решение задач
Задача 1. Велосипедист, двигаясь с постоянной скоростью, проехал 5 км за 10 минут. Какой путь проедет велосипедист за 45 минут?
Задача 2. Автомобиль ехал 2 часа со скоростью 75 км/ч. За какое время он продет это же расстояние, если будет ехать со скоростью 90 км/ч?
Алтын кесилиш
Геометрия имеет два сокровища: одно из них – Пифагорова теорема,
а второе – деление отрезка в среднем и крайнем отношениях...
Первое из них можно сравнить с мерой золота, а второе похоже на драгоценный камень.
Иоганн Кеплер
Отрезок прямой можно разделить, как на две равные части, так и на две неравные части в любом отношении. Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему: a:b=b:c или с:b=b:а
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если AB принять за единицу, BE = 0,382...
Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям. Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.
Существует предположение, что знание золотого деления Пифагор позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Шарль Эдуард Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий, изображенный на рельефе деревянной доски из гробницы Хесира, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления. Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В циркуле, который использовали в Помпеях, также заложены пропорции золотого деления. А термин золотое сечение ввел Леонардо да Винчи (1452-1519 гг)
Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.
Алтын кесилиштин пропорциясына геометриялык фигура негизделет. Жактарынын ушундай катыштагы тик бурчтугу алтын тик бурчтук деген аталышка ээ болгон. Разумеется есть и золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618.
Пропорции вокруг нас
Певучесть скрипки, красота ее голоса находится в прямой зависимости от того, в какой мере форма инструмента согласована с пропорцией золотого сечения. Анализ музыкальных произведений в диапазоне от Баха до Шостаковича продемонстрировал метрические отношения основных разделов музыкальных форм, а также золотое сечение. Таким образом, законы гармонии обнаружены в музыкальных рядах, в таблице Менделеева, в расстояниях между планетами, в микро- и макрокосмосе, во многих областях науки. Скульптура, архитектура, астрономия, биология, техника, психология и т. д. – везде так или иначе проявляет себя золотое сечение.
Полезные ссылки
- Видеоурок на тему «Прямая и обратная пропорциональные зависимости» [Электронный ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html (дата обращения: 24. 04. 2018)
- Видеоурок на тему «Пропорции»: [Электронный ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Proportsii.html (дата обращения: 24. 04. 2018)
- Теория пропорций: [Электронный ресурс] // 2006-2018 ФГАУ ГНИИ ИТТ "Информика" URL: http://files.school-collection.edu.ru/dlrstore/c4d6841c-5a1e-ab8e-3524-e712079e89f0/00145619554921908.htm (дата обращения: 24. 04. 2018)
Глоссарий
Отношение – это частное от деления одного числа на другое.
Пропорция – это равенство двух отношений.
Чи́сла Фибона́ччи — элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …, в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел.
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ, в честь древнегреческого скульптора и архитектора Фидия.Число Φ называется также золотым числом.
Библиография
- Белянин В.С. Владел ли Платон кодом золотой пропорции? Анализ мифа.: [Электронный ресурс] // Академия Тринитаризма URL: http://www.trinitas.ru/rus/doc/0016/001b/00161296.htm (дата обращения: 24. 04. 2018)
- Золотое сечение: [Электронный ресурс] // МОО «Наука и техника», 1997...2018 URL: http://n-t.ru/tp/iz/zs (дата обращения: 25. 04. 2018)
- Золотое сечение в дизайне сайтов: [Электронный ресурс] // 2016 UX Guide URL: http://uxguide.ru/dizajn/zolotoe-sechenie-v-dizajne-sajtov/ (дата обращения: 25. 04. 2018)
- Золотое сечение: [Электронный ресурс] // Блог Рунмастера | © 2006-2018 URL: http://rustimes.com/blog/post_1177437753.html (дата обращения: 25. 04. 2018)
- А. С. Пушкин. Сапожник. Притча: [Электронный ресурс] //Электронная публикация — РВБ, 2000—2018 URL: http://rvb.ru/pushkin/01text/01versus/0423_36/1829/0521.htm (дата обращения: 25. 04. 2018)
- 15 примеров золотого сечения в архитектуре. Jelena Shiljajeva M.A. in History of Art, University of Glasgow: [Электронный ресурс] //URL: https://arhi1.ru/ob-arhitekture/nauka/zolotoe-sechenie (дата обращения: 25. 04. 2018)
- Ле Корбюзье: [Электронный ресурс] //ArchAndArch.ru 2010-2018 URL: http://www.archandarch.ru/архитекторы/ле-корбюзье/ (дата обращения: 25. 04. 2018)
- Видеоурок на тему «Прямая и обратная пропорциональные зависимости» [Электронный ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html (дата обращения: 24. 04. 2018)
- Видеоурок на тему «Пропорции»: [Электронный ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Proportsii.html (дата обращения: 24. 04. 2018)
- Теория пропорций: [Электронный ресурс] // 2006-2018 ФГАУ ГНИИ ИТТ "Информика" URL: http://files.school-collection.edu.ru/dlrstore/c4d6841c-5a1e-ab8e-3524-e712079e89f0/00145619554921908.htm (дата обращения: 24. 04. 2018)
Правильное распределение энергий внутри дома, гармоничные конструкции в сочетании с экологией и безопасностью строительных материалов побуждают современных архитекторов и дизайнеров использовать принципы и понятия «Золотого сечения». Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.
Для талантливых художников и архитекторов правило сохраняется интуитивно во время творческого процесса. Однако некоторые из них сознательно реализуют это положение.
Известный французский архитектор Шарль Эдуард Ле Корбюзье для расчёта параметров будущего дома и интерьера использовал в качестве отправной единицы рост хозяина. Все его работы по-настоящему индивидуальны и гармоничны.
В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали. Для этого достаточно переставить мебель или сделать дополнительную перегородку. Аналогичным образом меняется высота и длина окон и дверей.
В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.
Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.
Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.
Архитектурные комплексы, которые расположены на территории Кыргызстана, занимают значительное место в истории зодчества народов Центральной Азии, соединив в себе лучшие достижения в области строительной техники, архитектуры и декоративного оформления своего времени.
Пропорциянын эң башкы эрежеси
Баардыгы билип эстеп калуу керек
Ортоңку мүчөлөрүн четкилерине көбөйтсөк
Бул мүчөлөрү дайыма тең болот.