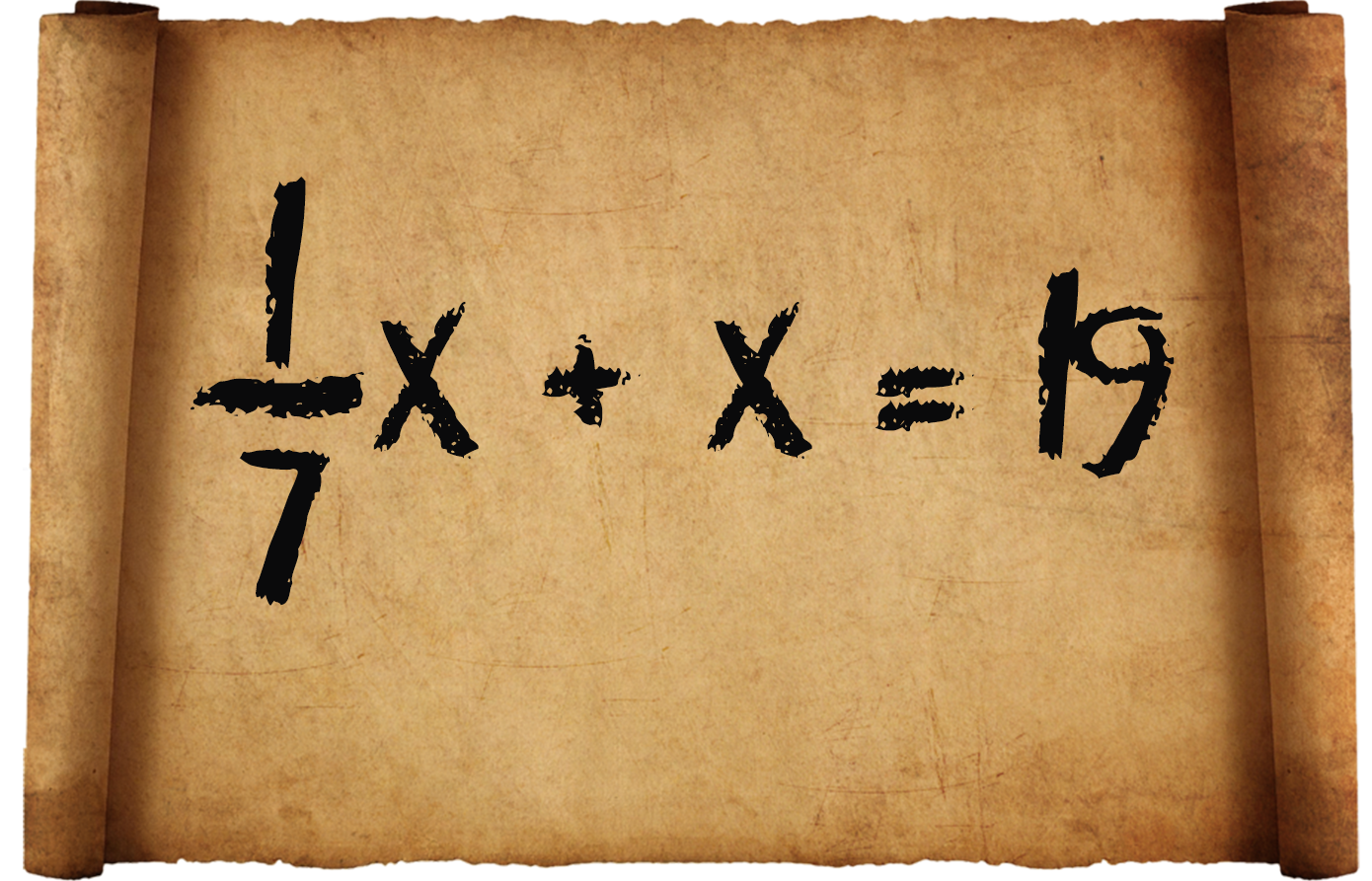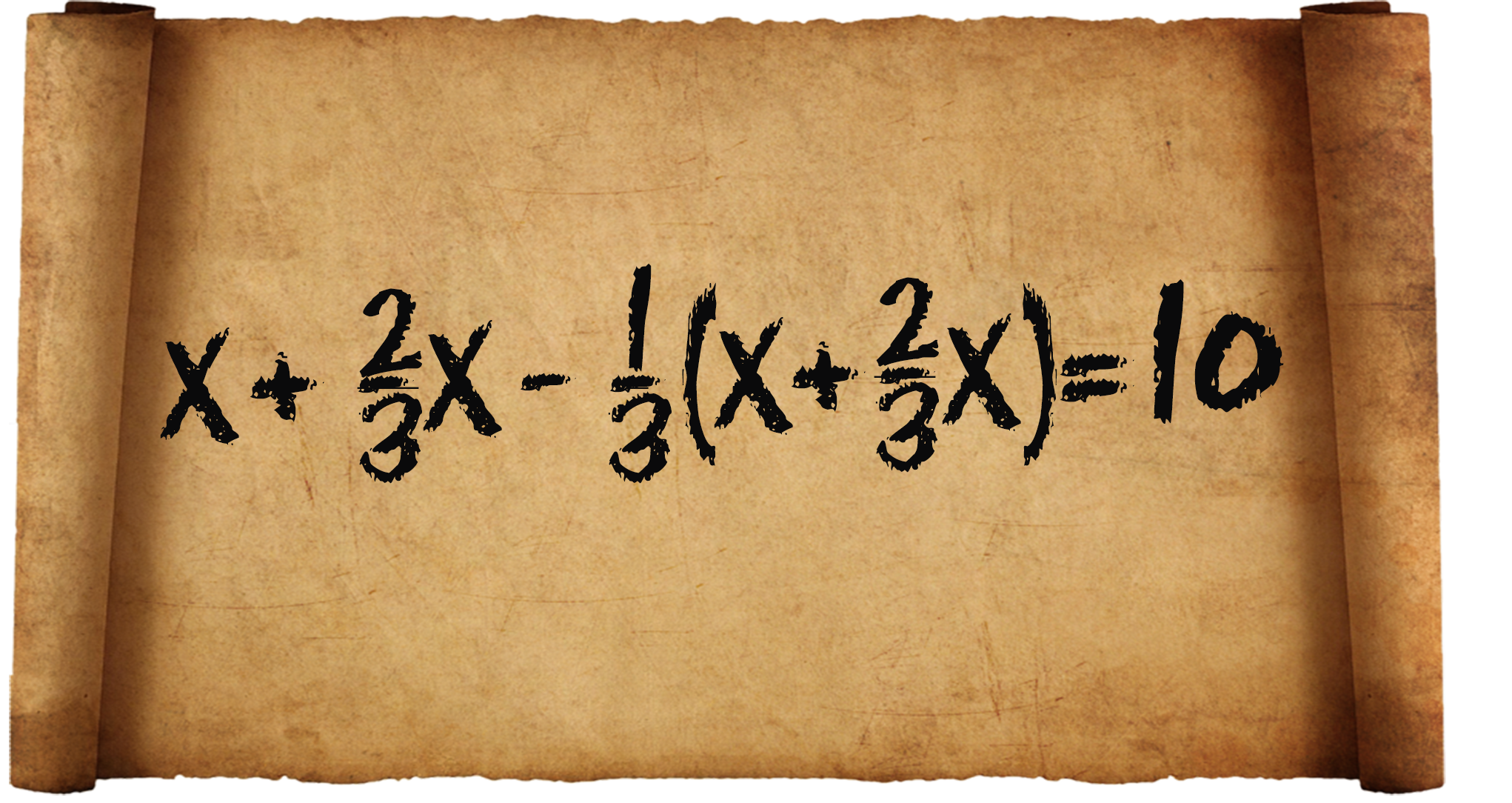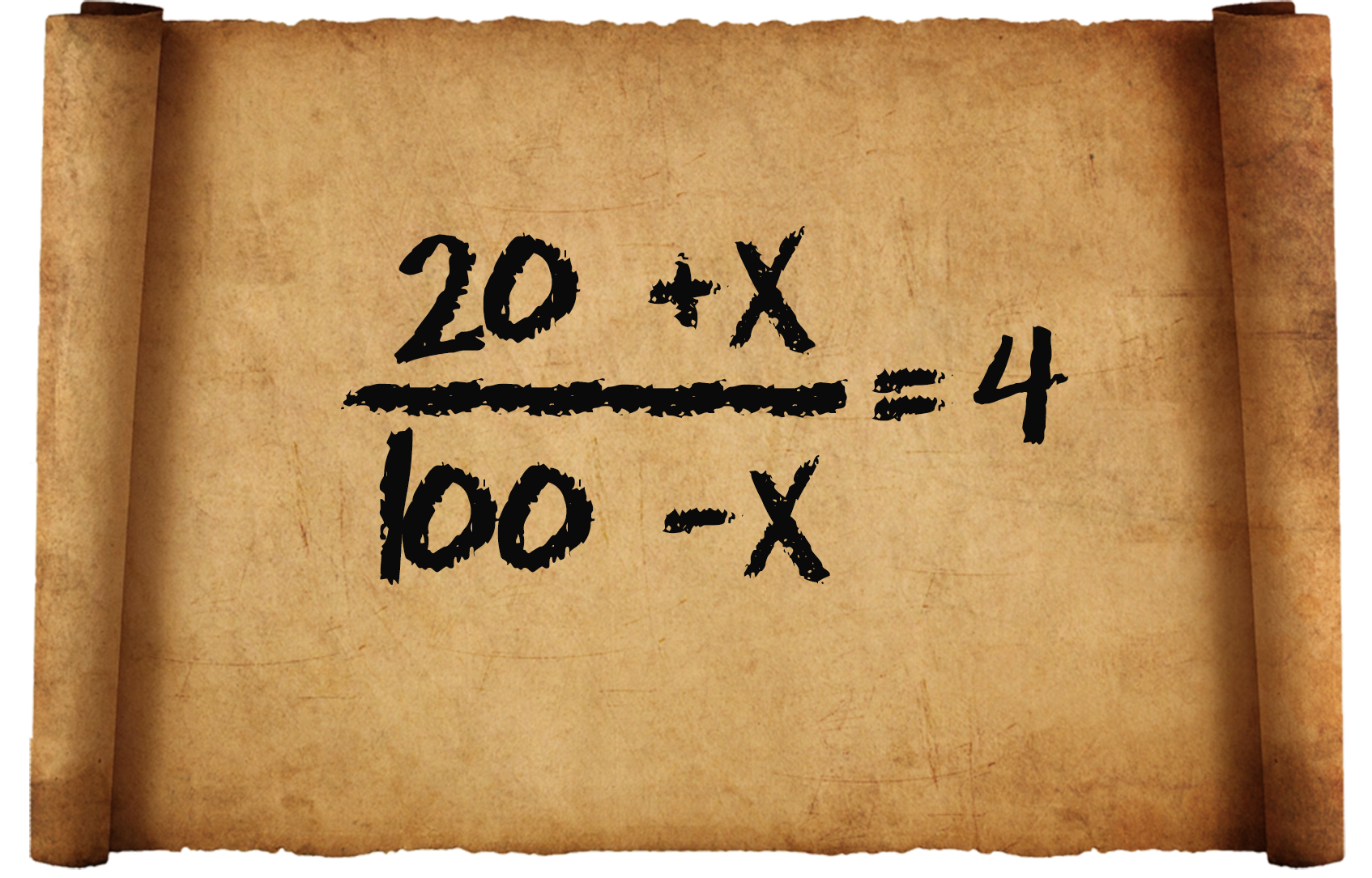БИЛИМ БУЛАГЫ

Теңдемелердин тарыхынан Кыргызстандагы математикалык илимдин өнүгүүсү Теңдемелер. Теңдемелердин тамыры Теңдемелер эмне үчүн керек.

Теңдемелердин тарыхынан

                                            Тендемелер мен үчун маанилүү, 
                                               анткени саясат – азыркы учур үчүн, 
                                               а теңдемелер – түбөлүк үчүн. 
                                             Альберт Эйнштейн.

Эң байыркы математикалык жазылмаларда эле амалдардын жардамы менен чыгарылган мисалдар жана амалдар кездешкен. Мындай Египеттик папируста биздин заманга чейин 2000 жыл мурун ( анда автор Ахмес жазгыч көрсөткөндөй, бул математикалык жазылмалар мындан да байыркы башка жазылмалардын көчүрмөсү) белгисиз санды табууга маселелер болгон. Ал белгисиз «хау» (дөбөчө) деп аталган жана өзгөчө иероглиф менен белгиленген.

Мына ал папирустун мисалдарынын чыгарылыштарынан:

1) 1) «Белгисиз, анын жетинчи бөлүгү, анын бүтүнү 19ду тузөт».

Азыркы кезде бул мисал мындайча жазылат:

• 
• 
• 

2) « кошулган жана алынган: калдыгы 10». Папируста маселенин чыгарылышын мындайча түшүнсө болот: белгисизге тү кошуп, андан алынган, келип чыккан суммадан; калдыгы 10; санды табуу керек. Азыркы кезде бул маселе мындайча жазылат:  ; Жообу: х=9

3) Диофантада дагы бир белгисизи менен амалдар кездешет, мисалы: “20 жана 100 сандары. Бир эле санды эң кичине санга кошуп жана эң чоңунан алуу; сумманын айырмага карата мааниси 4 кө барабар”.

4) Индиялыктардын биздин заманга чейинки VII жана VIII кылымдардагы арифметикалык кол жазмаларында, ал дагы андан дагы байыркы (III-IVкылымдардагы) кол жазманын көчүрмөсү, анда мындай маселе бар:

“Төрт курмандыктын экинчиси биринчиге караганда экиге көп берди, үчүнчүсү экинчиге караганда үчкө көп, төртүнчү үчүнчүдөн төрткө көп, баары биригип 132 беришти. Биринчи канчаны берди?”

Теңдемени жазсак: x+2x+6x+24x=132

Кол жазмаларда бул маселе “жалган абал” ыкмасы менен чыгарылат. (Бул ыкманы Л.Ф.Магницкий өзүнүн “Арифметикасында” пайдаланган.)

“Эгерде биринчи 1ди берсе, анда экинчи 2ни, үчүнчү 6, төртүнчү 24, баары чогуу 33. Бирок баары бирге 132 болчу да, башкача айтканда төрткө көп. Демек, ар бир курмандык төрткө көп беришкен”. Жооп: 4;8;24;96.

Бирок биринчи даражадагы бир белгисизи менен теңдемени чыгаруунун жалпы эрежесин IX кылымда Мухаммед аль-Хорезми берген.

Өзүнүн “Аль-джебр жана аль-мукабала” аттуу жазылмаларында ал теңдемени чыгаруудагы колдонулган эки абалды берген:

1) “аль-джебр” абалы, эгерде теңдемеде терс (алынуучулар) мүчөсү болсо, анда аларды теңдеменин эки жагынын тең карама-каршы мүчөлөрүнө кошулат, анда теңдеменин баардык мүчөлөрү оң болот.

2) “аль-мукабала” теңдеменин эки жагынан тең бирдей мүчөсү алынат, бул болсо аны жөнөкөйлөткөнгө алып келет.

Мисалы, Берилди: 5х-17=2х-5.

“аль-джебрды” пайдалансак: теңдеменин ар бир бөлүгүнө 5 менен 17и кошобуз.

Анда: 5х+5= 2х+17 алабыз.

“аль-мукабала”: Ар бир бөлүктөн 2х менен 5 ти алабыз.

Анда: 3х=12 ни алабыз.

Бул жерден х ти табуу оңой болот. x=4

В начало

Кыргызстандагы математикалык илимдин өнүгүүсү

Математика мектепте предмет катары Кыргызстанда Октябрь революциясынан кийин, жогорку математика болсо – Кыргызстанда биринчи ЖОЖ – Кыргыз мамлекеттик педагогикалык институту – азыркы Ж. Баласагын атындагы Кыргыз улуттук университети ачылгандан кийин окутула баштаган.

Кыргызстанда математика боюнча системалуу изилдөө иштери 1940-ыжлдан тартып семинарда профессор Г. А. Сухомлиновдун жетекчилиги астында жүргүзүлө баштаган. 1949-1965-жылдары семинарларды 1960-жылы Кыргыз ССРдин ИА мүчө-корреспонденти болгон профессор Я. В. Быков жетектеген, 1966-жылдан тартып бул семинарларды жалпыреспубликалык болуп, Институттун дубалында Кыргыз ССРдин ИА академиги (1979) жана СССРдин ИА (1981) мүчө-корреспонденти М. И. Аманалиев жетекчиликке алган.

1955-жылы Кыргыз ССРдин ИА Президиумунун астында, ал убакта эле илимдин кандидаттары Я. В. Быков жана М.И. Иманалиевдер курамында болушуп, Физика, математика жана механика бөлүмүн түзүшкөн.

1960-жылы Бөлүм Физика, матеатика жана механика Институту болуп өзгөртүлгөн. 1962-жылы ал Физика жана математика Институту аталып, 1984-жылы Физика жана математика Институтунун базасынын математикалык лабораториясынын базасында Математика институту уюштурулган. 2008-жылы анын базасында Теориялык жана прикладдык математика институту түзүлүп, а 2017-жылы ал КР УИА Математика институту болуп кайра аталган.

1984-жылдан 2016-жылга чейин Институтту М. И. Иманалиев жетектеген, а 2016-жылдан тартып бүгүнкү күнгө чейин академик А. А. Бөрүбаев жетектеп келет. Институттун негизги ишмердүүлүгү төмөнкү илимий изилдөөчүлүк багыттарды аныктайт:

• Тең калыптагы жана топологиялык тегиздиктер жана алардын чагылдырылышы.
• Функционалдык мейкиндик.
• Айырмасын, дифференциялдык жана интегро-дифференциялдык теңдемелерди түшүндүргөн, анын ичинде сингулярдык-кыжырдануучу динамикалык систкемалары.
• Интегралдык теңдемелер, корректүү эмес жана текери маселелер.
• Оптимизацияланган экономикалык маселелер.

Илимий изилдөөлөрдү компьютерлештирүү, объектилерди интерактивдүү таануу.

Изилдөө иштеринде көбүнчө теория жана интегро-дифференцирленген тиркемелерге, интегралдык жана дифференциалдык теңдемелерге, операциялык изилдөөлөргө, айырмачылык жана суммардык-айырмачылык теңдемелерге, математикалык физикага, сызыктуу алгебрага. Кыргызстандын математикадагы көпчүлүк ийгиликтери интегро-дифференциялдык теңдемелер чөйрөсүндө жетишилген. Математик окуумуштуулар математикалык илимге билимдүү, жогоркуинтеллектуалдуу, максатка умтулган жаш адистер келип Кыргызстанды мындан дагы жогорку бийиктиктерге жетишүүгө зор салымын кошооруна ишенишет.

• 
• 
• 
• 
• 
• 
• 

В начало

Теңдемелер. Теңдемелердин тамыры

Равенство с переменной называют уравнением.

Каждое значение переменной, при котором данное уравнение превращается в верное равенство, называется корнем уравнения. Решить уравнение - это значит найти все его корни или доказать, что их нет. Уравнение может иметь один, два, несколько, множество корней или не иметь их вовсе.

Пример 1. Уравнение 5 + x = 15 имеет единственный корень x = 10, так как только при этом значении переменной 5 + x = 15 является верным равенством.

Пример 2. Уравнение (5 + x)(x - 6)=0 имеет два корня: -5 и 6.

Пример 3. 9 + x² = 0 не имеет корней на множестве вещественных чисел.

Линейные уравнения

Линейным уравнением с одной переменной х называют уравнение вида ax = b, где a, b –вещественные числа; а называют коэффициентом при переменной, b - свободным членом.

• 
• 

Равносильность уравнений

Уравнения, имеющие одни и те же корни, называются равносильными уравнениями. Равносильными считаются и уравнения, у которых нет корней.

Пример 4. Уравнения x + 5 = 7 и x - 8 = -6 равносильны, так каждое из них имеет единственный корень, равный 2.

Пример 5. Уравнения 9 + x² = 0 и 3x² + 27 = 0 равносильны, так как каждое из них не имеет корней.

Пример 6. Уравнения 9 - x² = 0 и x + 4 = 7 неравносильны, так как первое уравнение имеет два корня: 3 и -3, а второе только один корень: 3.

Когда уравнение решают, его стараются заменить на более простое, равносильное данному. Поэтому необходимо знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.

Теорема 1. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.

Например, уравнение x² + 4 = 2x равносильно уравнению x² + 4 - 2x = 0.

Теорема 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Например, уравнение (x-5)/4 =4x равносильно уравнению x-5=16x.Обе части первого уравнения умножили на 4.

Рассмотрим на примерах решение уравнений.

• 
• 
• 

В начало

Теңдемелер эмне үчүн керек

Эсептөөчү маселелер түз жана кыйыр түрүндө болот. Биринчисинин чыгарылышына маселенин шарты түрткү кылат, ал эми кыйыр түрүндөгү маселелердин шарты анын чыгарылышына кандай алып бараары белгисиз болот. Мындан арифметикалык аталыштагы чыгарылышты кыйыр түрүндөгү маселелердин чыгарууда чоң чыгармачылыкты талап кылат. Ар бир жаңы маселе жаңыча пландоого алып келет. Эсептөө процессин алып кетүү үчүн негизги предмети болгон алгебраны окуп үйрөнүүдө теңдеменин ыкмасы түзүлгөн. Ошондон улам, теңдемени эсептөө процессин кыймылдатуу керек. Теңдеме түзүлгөндөн соң, анын чыгарылышын атоматтык түрдө дароо алсак болот. Маселени чыгаруунун кыйынчылыгы ал теңдеменин түзүлүшүнө жараша келип чыгат.

Теңдемени түзүү – бул маселенин белгилүүлөрү менен анын чоңдуктарынын белгисиздери ортосундагы байланышты математикалык формада туюндуруу.

Теңдемелердин жардамы менен маселелерди чыгарууну карайлы.

1-маселе. Апасы уулунан эки эсеге улуу. Он жыл мурун ал баласынан үч эсе улуу болчу. Апасы канча жашта?

2-маселе. Үч кутучада 56 калем сап бар. Биринчи кутучадагы калем саптарэкинчисине караганда эки эсе, ал эми үчүнчүсүнө караганда 2,5 эсеге көп экендиги белгилүү. Ар бир кутучуда канчадан калем сап бар?

3-маселе. Дарыянын агыбы боюнча теплоход жолду 9 саатта сүзүп өтөт. Агымга каршы 11 саатта. Эгерде дарыянынагымынын ылдамдыгы 2 км/с болсо теплоходдун өзүнүн ылдамдыгын тапкыла.

• 
• 
• 

В начало

Пайдалуу шилтемелер

Первоначальные способы решения уравнений были достаточно сложными и разнообразными. В процессе развития математики произошло их значительное упрощение, и для каждого типа уравнений появился единый алгоритм решения. Более подробно можете увидеть: [Электронный ресурс] // novykrug YouTube, 2018. URL:https://www.youtube.com/watch?v=WpwOQHVB5s4 (дата обращения: 28. 04. 2018)

Математикалык модель – бул реалдуу жашоо кырдаалдарын (маселелерди) математикалык тилдин жардамы менен түшүндүрүү ыкмасы. Биздин этапта алгебраны окуп-үйрөнүүдөгү маселелерди чыгарууда математикалык моделдөөнү колдонобуз.: .:[Электрондук ресурс] // school-assistant.ru © 2016 URL: http://school-assistant.ru/?predmet=algebra&theme=matemat_model (кайрылуу датасы: 28. 04. 2018)

Сызыктуу теңдемени колдонуу биздин жашообузда абдан кеңири колдонулат. Алар көптөгөн эсептөөлөрдо, имараттарды курууда жана да спортто да колдонулат. Адам баласы сызыктуу тендемени байыртадан бери колдонуп келүүдө жана азыр да колдонуу деңгээли өсүүдө. Сызыктуу теңдеме өзүнө алгебралык теңдемени түшүндүрүп, көп мүчөлөрдүн толук даражалары бирге барабар болот. Бул теңдемелержи чыгаруунун көптөгөн ыкмалары бар. Бул теңдемелерди чыгарууда өзгормөнүн маанисин табуу зарыл.: [Электрондук ресурс] // © Pocket Teacher. https://pocketteacher.ru/linear-equations-2-ru (кайрылуу датасы: 28. 04. 2018)

В начало

Глоссарий

• Алгебра – бул ар түрдүү чоңдуктагы жана чыгарылыштагы теңдемелердин үстүнөн болгон амалдардын жана бул амаладарга тиешелүү касиеттерин үйрөтүүчү математиканын бөлүмү.
• Чыныгы сандар (латындан realis — чыныгы) – айлана чөйрөдөгү геометриялык жана физикалык чоңдуктарды ченөө зарылдыгынан келип чыккан, ошондой эле тамырдан чыгаруу, логарифманы эсептөө, алгебралык теңдемелерди чыгаруу, функцияларды изилдөө сыяктуу эсептөөлөрдү жүргүзүүгө арналган математикалык объект.
• Квадраттык теңдеме – бул ax² + bx + c = 0 түрүндөгү теңдеме, мында a, b жана c — коэффициенттери каалагандай сандар, мында a ≠ 0.

В начало

Библиография

• Математическая модель. Правила http://school-assistant.ru/?predmet=algebra&theme=matemat_model
• Основные математические знаки и символы: [Электронный ресурс] // 2013-2018 «SYL.ru» URL: https://www.syl.ru/article/327248/osnovnyie-matematicheskie-znaki-i-simvolyi (дата обращения: 26. 04. 2018)
• Институт математики.:[Электронный ресурс] // 2016-2017 Национальная академия наук КР URL:http://naskr.kg/index.php/ru/struktura-nan-kr/nauchno-issledovatelskie-uchrezhdeniya/institut-matematiki (дата обращения: 28. 04. 2018)
• Линейное Уравнение - Решение С Помощью Онлайн Решателя:[Электронный ресурс] // © Pocket Teacher. https://pocketteacher.ru/linear-equations-2-ru (дата обращения: 28. 04. 2018)
• Развитие математической науки Кыргызстана:[Электронный ресурс] //2018 © Институт Математики URL: http://math.aknet.kg/home/science-develop.pdf
• В.А. Гусев, А.Г. Мордкович Математика. Справочные материалы М.: Просвещение, 1988.
• Федин С. Н. Математики тоже шутят. — 4-е изд. — М.: УРСС, 2012. — 216 с.

В начало

Основные математические знаки

Кошуу жана кемитүү белгилерин немис математикалык мектебиндеги алгебраистер тарабынан ойлонуп табылган. Алар Иоганн Видмандын (Johannes Widmann) 1489-жылы чыгарылган “Арифметикасында” колдонушкан. Ага чейин кошуу p (plus) тамгасы менен белгиленген же et латын сөзү менен (“жана” союз), а кемитүү m (minus) тамгасы менен белгиленген. Видмандын плюс символу кошууну эле эмес “жана” союзун да өзгөрткөн. Бул белгилердин чыгып келиш таржымалы белгисиз, арийне ал мезгилде бул символдорду же белгилерди соода-сатык иштеринде пайда жана жоготууну белгилешкен экен. Бул эки символ көз ирмемде жарым кылым эски белгини колдонуп келген Италиядан башка Европанын бүт аймагына тез тарап кеткен.

Көбөйтүү белгисин 1631-жылы Уильям Отред (Англия) кыйгач кайчылаш белги түрүндө киргизген. Ага чейин М белгиси колдонулуп келген. XVII кылымдын аягында Лейбниц кайчылаш белгини х белгиси менен чаташтырбоо үчүн чекит менен алмаштырган; буга чейн мындай белги Региомонтанада (XV кылым) жана англия окумуштуусу Томас Хэрриотдо (1560—1621) кездешкен.

• 
• 

Бөлүү белгиси. Отред кыйгач сызыкчаны туура көргөн. Кош чекит менен Лейбниц белгилөө жүргүзгөн. Аларга чейин көпчүлүк учурда D тамгасын колдонушкан. Фибоначчиден баштап араб жазылмаларындагыдай бөлчөк сызууну колдонушкан. Англиядан жана АКШда XVII кылымдын орто ченинде Йоханн Ран жана Джон Пеллдер сунушташкан ÷ (обелюс) символу тараган.

• 
• 
• 

Барабар белгисин (1510—1558) 1557-жылы Роберт Рекорд сунуштаган. Ал дүйнө жүзүндө жарыш түрүндө барабар узундукка ээ болгон башка бир да белги жок деген. Континенталдык Европада барабар белгисин Лейбнциц киргизген.

• 
• 
• 

“Барабар эмес” белги алгач жолу Эйлерде кездешкен. Салыштыруу белгисин өзүнун өлөөр алдындагы 1631-жылы чыгарган жазылмасында көрсөткөндөй Томас Хэрриот киргизген. Ага чейин: чоң, кичине сөздөрү менен жазышкан. Катуу салыштыруу символун Джон Валлис сунуштаган. Алгач сызыкча салыштыруу белгисиненен жогору болуп, а анын астында азыркыдай болгон.

Математика – как высокая винтовая лестница,

чтобы взойти по ней к вершинам знаний,

надо пройти каждую ступеньку от первой до последней.

Американский математик Джордж Бернард Данциг , будучи аспирантом университета, однажды опоздал на урок и принял написанные на доске уравнения за домашнее задание. Оно показалось ему сложнее обычного, но через несколько дней он смог его выполнить. Оказалось, что он решил две «нерешаемые» проблемы в статистике, над которыми бились многие учёные.

Решаем уравнения на Android за 1 секунду

Школьник зашел в лавочку возле школы. На прилавке лежали ручки по 30 рублей за штуку и карандаши по 15 рублей. Мальчик приобрел один карандаш и пошел к выходу, но по дороге подумал: «Я уже отдал продавцу 15 рублей, значит, если вернуть покупку, в сумме на моем счету окажется 30 руб». Сможет ли школьник теперь купить ручку? Почему?

Ответ

Не сможет.

В качестве объяснения приведем небольшую шутку.

Студент заказал в кафе булочку, но затем решил, что не слишком голоден и обменял ее на чашечку кофе. Выпив напиток, он направился к выходу, не расплатившись. Cамо собой, за ним побежала буфетчица.

- Вы не заплатили за кофе!

- Да, все верно, но я же взял его взамен булочки!

- Так булка тоже не оплачена!

- Верно, но я ведь ее и не ел!

2. Перед вами неверное неравенство 7+4-4=0.Как, переложив одну спичку, сделать его правильным?

3. Реши кроссворд.

По горизонтали.

4. Равенство двух отношений.

5. Французский математик, который установил связь между коэффициентами уравнения и его корнями.

По вертикали.

1. Значение переменной в уравнении.

2. Равенство, содержащее переменную.

3. Уравнение вида ax=b.

4. Неизвестное число в уравнении.