Математика: Координаты на плоскости
История возникновения координат
История возникновения координат и формирование системы координат берет начало в древнем мире, благодаря развитию таких наук как астрономия, география, живопись. Древнегреческого ученого Анаксимандра Милетского (ок. 610-546 до н. э.) считают составителем первой географической карты. Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести хорошо известные теперь географические координаты: широту и долготу - и обозначить их числами. Идея изображать числа в виде точек, а точкам давать числовые обозначения зародилась в далекой древности. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта.
Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Говорят, эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650) – того самого, чьим именем названы прямоугольные координаты. Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль из-за отсутствия элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.
Вклад в развитие координатного метода внес также Пьер Ферма. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке. А вот термины «абсцисса», «ордината» и «координаты» были впервые введены Вильгельмом Лейбницем в семнадцатом веке.
Координаты на плоскости
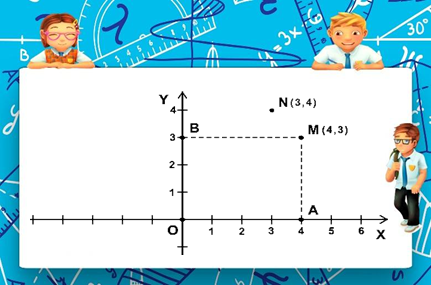
Проведем две перпендикулярные координатные прямые x и y , которые пересекаются в начале отсчета — точке О. Эти прямые называют системой координат на плоскости, а точку О — началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Пусть M - некоторая точка плоскости. Проведем через нее прямую MA, перпендикулярную координатной прямой x, и прямую MB перпендикулярную координатной прямой y. Так как точка A имеет координату 4, а точка B координату 3, то положение точки M определяется парой чисел (4, 3). Эту пару чисел называют координатами точки M. Число 4 называют абсциссой точки M, а число 3 — ординатой точки M. Координатную прямую x называют осью абсцисс, а координатную прямую y — осью ординат. Точку М с абсциссой 4 и ординатой 3 обозначают так: M (4, 3). На первом месте пишут абсциссу точки, а на втором ее ординату. Если переставить координаты местами, то получится другая точка N (3, 4), которая тоже изображена на рисунке.
Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината, и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Оси координат разбивают плоскость на четыре части – четверти I, II, III, IV. В пределах одной четверти знаки обеих координат сохраняются. В первой четверти они положительны, во второй – абсцисса отрицательна, а ордината положительна, в третьей – абсцисса и ордината отрицательны ,а в четвертой – абсцисса положительна, а ордината отрицательна.
Точки оси х имеют равные нулю ординаты (у=0), а точки оси у – равные нулю абсциссы (х=0). Абсцисса и ордината начала координат равны нулю.
Пример 1 . На координатной плоскости отметьте точки А (1; 3), В (0;-4) , С (-3;-2)
Перпендикулярные прямые
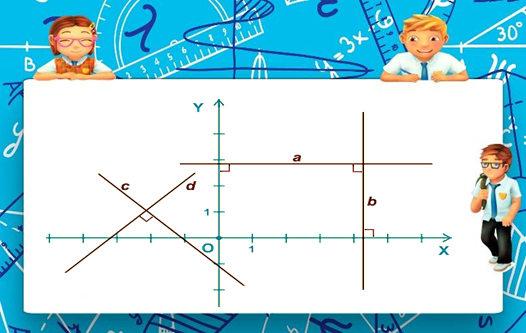
Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.
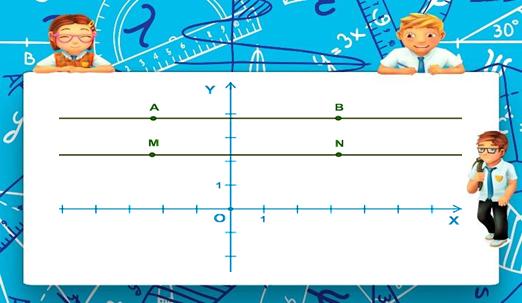
На рисунке изображены прямые a и b, они перпендикулярны друг другу и осям координат. Пишут a ⊥b,a ⊥Oy,b⊥Ox. Если прямая a ⊥b , то ,b⊥a. Прямые c и d перпендикулярны друг другу, но не перпендикулярны осям координат. Пишут c ⊥d.
Параллельные прямые
Две различные прямые могут либо пересекаться в одной точке, либо не пересекаться. Две непересекающиеся прямые на плоскости называют параллельными. Пишут AB∥MN. Эту запись читают так: «Прямая AB параллельна прямой MN». Если AB∥MN , то MN∥AB.
Попробуйте самостоятельно решить эти задания. А верность ответов можно проверить с помощью видео, которое идет сразу после примеров.
Пример 2. На координатной плоскости через точку А (-4; 3) проведена прямая, параллельная оси ординат, а через точку В (5; -2) проведена прямая, параллельная оси абсцисс. Отметь точку пересечения этих прямых.
Пример 3. Дан прямоугольник ABCD и координаты его вершин А (3; 4), В (-5; 4), С (-5; -3). Отметьте на координатной плоскости вершину D.
Пример 4. Даны точки А (х; 2) и В (3; - 3). Известно, что прямая АВ перпендикулярна оси абсцисс. Найди значение х.
Координаты в повседневной жизни
Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
Идея изображать числа в виде точек, а точкам давать числовые обозначения зародилась в далекой древности. Первоначальное применение координат связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта.
Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту. До наших времён дошла такая история, которая подтолкнула его к открытию. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650)– того самого, чьим именем названы прямоугольные координаты. Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.
Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Кроме того, в своей работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. «Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
А вот термины «абсцисса», «ордината» и «координаты» были впервые введены Вильгельмом Лейбницем в семнадцатом веке.
Проведем две перпендикулярные координатные прямые — и , которые пересекаются в начале отсчета — точке О. Эти прямые называют системой координат на плоскости, а точку О —началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Пусть М - некоторая точка плоскости. Проведем через нее прямую МА, перпендикулярную координатной прямой X, и прямую XB перпендикулярную координатной прямой Y. Так как точка A имеет координату 4, а точка B координату 3, то положение точки M определяется парой чисел (4, 3) . Эту пару чисел называют координатами точки M. Число 4 называют абсциссой точки M, а число 3 — ординатой точки M. Координатную прямую X называют осью абсцисс, а координатную прямую Y — осью ординат. Точку M с абсциссой 4 и ординатой 3 обозначают так: M (4, 3). На первом месте пишут абсциссу точки, а на втором ее ординату. Если переставить координаты местами, то получится другая точка N (3, 4) , которая тоже изображена на рисунке. Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината, и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Для того, чтобы нанести точки на координатную плоскость, Вы должны понимать организацию координатной плоскости и знать, что делать с координатами (х,у) https://www.youtube.com/watch?v=aOhVGfdRtgU .
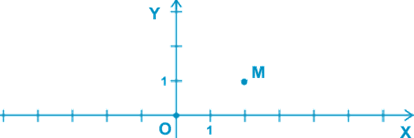
Пример. Выберите точку, изображенную на координатной плоскости.
Ответ: Точка М имеет координаты (2;1).
Перпендикулярные прямые.
Две прямые, образующие при пересечении прямые углы, называют перпендикулярными. На рисунке изображены прямые a и b, они перпендикулярны друг другу и осям координат.
Прямые и перпендикулярны друг другу, но не перпендикулярны осям координат. Пишут: .
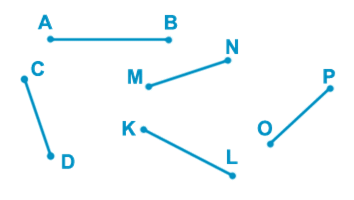
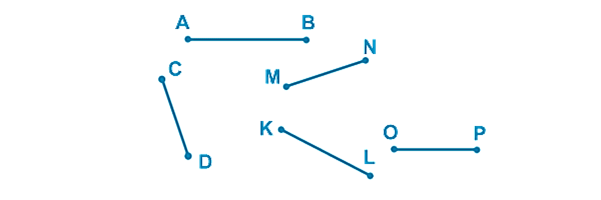
Пример. Выберите отрезки, лежащие на перпендикулярных прямых.
Ответ: CD и OP
Параллельные прямые
Две различные прямые могут либо пересекаться в одной точке, либо не пересекаться. Две непересекающиеся прямые на плоскости называют параллельными. Пишут: ABMN . Эту запись читают: "Прямая AB параллельна прямой MN". Если ABMN, то MNAB .
Пример. Выберите отрезки, лежащие на параллельных прямых.
Ответ: AB и OP.
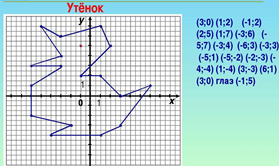
Рисуем по координатам
Суть задания заключается в том, чтобы по заданным координатам точек построить на координатной плос¬кости некоторое изображение, при этом построенные точки, как правило, последовательно соединяют плавной линией.
Глоссарий
1. Числовая ось - прямая, на которой изображаются действительные числа
2. Абсцисса - лат. abscissa-отсекаемый (отрезок на оси иксов).
3. Ордината - лат. ordinatus – упорядоченный.
4. Координаты — величины, определяющие положение точки на плоскости .
5. Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
6. Симметрия — слово греческого происхождения, означает соразмерность, наличие определённого порядка, закономерности в расположении частей.
7. Веб-картография - это область компьютерных технологий связанная с доставкой пространственных данных конечному пользователю.
Полезные ссылки
Научить свободно ориентироваться на координатной плоскости, строить точки по заданным ее координатам и определять координаты точки, отмеченной на плоскости; четко и аккуратно выполнять построения, развивать творческие способности; воспитывать интерес к предмету http://rudocs.exdat.com/docs/index-350736.html
Библиография
- Веб-ГИС (Компьютерра, 749, 2008): [Электронный ресурс] // GIS-Lab и авторы, 2002-2018 URL: http://gis-lab.info/qa/webgis.html (дата обращения: 16. 04. 2018)
- Гравюры Дюрера:[Электронный ресурс] // Gallerix 2009 - 2018. URL: https://gallerix.ru/storeroom/1780068273/ (Дата посещения: 14.04.2018)
- Лев Генденштейн «Алиса в стране математики»: [Электронный ресурс] // ЛитЛайф - литературный клуб URL: https://litlife.club/br/?b=282306 (Дата посещения: 14.04.2018)
- Координаты в повседневной жизни:[Электронный ресурс] //Математика, решение онлайн!!! 2018. URL: https://matemonline.com/2013/08/koordinaty-v-povsednevnoj-gizni/ (Дата посещения: 14.04.2018)
- Осевая и центральная симметрия: [Электронный ресурс] // ООО ЯКласс 2018. URL: http://www.yaklass.ru/p/matematika/6-klass/geometricheskie-figury-i-tela-simmetriia-na-ploskosti-13781/osevaia-i-tcentralnaia-simmetriia-14716/re-e5fbbd9b-0519-4f8d-88ee-4bdcfa44b87b (Дата посещения: 14.04.2018)
- Системы координат, применяемые в геодезии и топографии: [Электронный ресурс] // «ФБ», 2017 URL: http://fb.ru/article/352671/sistemyi-koordinat-primenyaemyie-v-geodezii-i-topografii (дата обращения: 16. 04. 2018)
- Координаты. Декартова система координат.: [Электронный ресурс] //Calc.ru 2000-2018 URL: https://www.calc.ru/Koordinaty-Dekartova-Sistema-Koordinat.html (дата обращения: 16. 04. 2018)
- "Система координат" в рамках IV регионального сетевого математического проекта "Системы координат: взгляд в прошлое и в настоящее".: [Электронный ресурс] // ООО CALAMEO URL: https://ru.calameo.com/read/001079152e4dd53000844 (дата обращения: 16. 04. 2018)
- Системы координат древности: [Электронный ресурс] // HintFox 2015 URL: http://www.hintfox.com/article/sistemi-koordinat-drevnosti.html (дата обращения: 16. 04. 2018)
- Карта Бишкека: [Электронный ресурс] //OpenStreetMap contributors, API 2GIS URL: https://2gis.kg/bishkek (дата обращения: 16. 04. 2018)
- Гугл карты:[Электронный ресурс] // Google 2018. URL: https://www.google.ru/maps/@26.4677171,28.1395614,20599069m/data=!3m1!1e3 (дата обращения: 16. 04. 2018)
- В.А. Гусев, А.Г. Мордкович Математика. Справочные материалы М.: Просвещение, 1988.
Как по вашему, может ли пригодиться в повседневной жизни знания о координатной плоскости? И доводилось ли вам слышать такую фразу, как «оставьте свои координаты» или «по каким координатам вас можно найти»? И задумывались ли вы над тем, что может обозначать эти выражения?
Оказывается все очень просто и банально и это значит местонахождение того или иного объекта, по которому легко найти человека или какое-то определенное место. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно: например
Чтобы пойти в гости к однокласснику, недостаточно знать только дом, в котором он живет, а нужно еще и знать номер квартиры.
При покупке билетов на поезд, вы знаете не только его номер и место назначения, но и обязательно должен быть указан номер вагона и места.
Чтобы найти свое место в зале, сначала мы ищем свой ряд, затем свое место.
Для введении игры Морской бой тоже необходимо знать координаты
Все встают из-за парт. На экране появляются координаты точек. Если точка принадлежит первой четверти, ребята должны потянуться. Если второй – наклониться вперед. Третьей – руки в стороны. Четвертой – сделать «восьмерку» сцепленными руками. Если точка находится на оси – хлопнуть в ладоши.