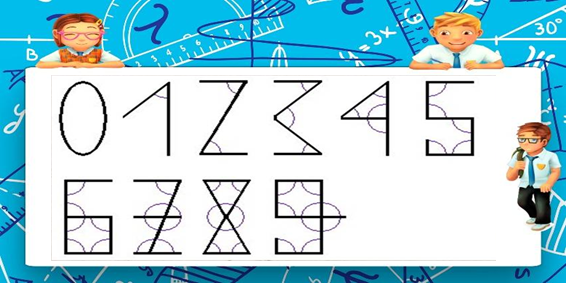Математика: Чыныгы сандар
Версия от 15:25, 16 апреля 2018; Msu05 (обсуждение | вклад) (Новая страница: «__NOTOC__ <div class="row mat-bg"> <div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> {{Якорь|Начало}} <div clas…»)
Первая развитая числовая система, построенная в Древней Греции, включала только натуральные числа и их отношения (пропорции, в современном понимании — рациональные числа). Однако вскоре выяснилось, что для целей геометрии и астрономии этого недостаточно: например, отношение длины диагонали квадрата к длине его стороны не может быть представлено ни натуральным, ни рациональным. Для выхода из положения Евдокс Книдский ввёл, в дополнение к числам, более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма, теория Евдокса — это геометрическая модель вещественных чисел.
Ситуация начала меняться в первые века н. э. Уже Диофант Александрийский, вопреки прежним традициям, рассматривает дроби так же, как и натуральные числа, а в IV книге своей «Арифметики» даже пишет об одном результате: «Число оказывается не рациональным». После гибели античной науки на передний план выдвинулись индийские и исламские математики, для которых любой результат измерения или вычисления считался числом. Эти взгляды постепенно взяли верх и в средневековой Европе, где поначалу разделяли рациональные и иррациональные (буквально: неразумные) числа (их называли также мнимыми, абсурдными, глухими и т. п.). Полное уравнение в правах иррациональных чисел связано с трудами Симона Стевина (конец XVI века). Спустя столетие Ньютон в своей «Универсальной арифметике» (1707) даёт классическое определение (вещественного) числа как отношения результата измерения к единичному эталону.
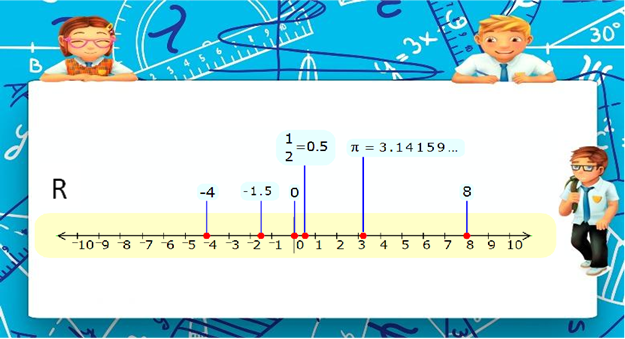
Вещественное, либо действительное число — математическая абстракция, которая возникла из необходимости в измерении геометрических и физических величин окружающего мира, кроме того, в проведении таких действий как извлечение корня, вычисление логарифмов, решение алгебраических уравнений. Это число можно представить как отношение 2-х величин с одной размерностью, либо описывающее положение точек на прямой.
Множество вещественных чисел обозначают как R («полужирное R») (англ. blackboard bold «R») от лат. realis —действительный и зачастую называют вещественной либо числовой прямой. Официально вещественные числа строятся на основе более простых объектов. Например, целых и рациональных чисел.
Полезные ссылки
Исторически первыми числами, с которыми познакомился человек, были натуральные числа: 1, 2, 3, и т.д. С помощью таких чисел можно было посчитать какое¬-нибудь количество целых предметов, однако, натуральные числа имели очень большой недостаток. А вот вещественных чисел действительно больше, чем натуральных чисел в бесконечное число раз. Невозможно придумать способ сосчитать все вещественные числа с помощью натуральных чисел. Более подробно: http://wreferat.baza-referat.ru/Вещественные числа.
Загадки
Глоссарий
- Положительные числа- число, большее нуля.
- Отрицательные числа- это числа со знаком минус (−), например −1, −2, −3 и т.д. Читается как: минус один, минус два, минус три и т.д.
- Целые числа– это натуральные числа, число нуль, а также числа, противоположные натуральным.
- Натуральные числа- это числа, которые используются для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов.
- Рациональные числа-это числа, которые можно записать в виде положительной обыкновенной дроби, отрицательной обыкновенной дроби или числа нуль.
- Иррациональные числа- числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби.
- Мантисса-целая часть числа
Библиография
1. Множества вещественных чисел: http://life-prog.ru/1_21894_veshchestvennie-chisla.html
2. Видеоурок на тему «Вещественные числа» https://www.youtube.com/watch?v=WrIXyM_rv-Y
3. Видеоурок на тему «Иррациональные числа» https://www.youtube.com/watch?v=W3AyQn6NJ64
4. Видеоурок на тему «Модуль действительного числа и его свойства» https://www.youtube.com/watch?v=KbtNg7n9GpU
1. Изначально арабские цифры состояли только из прямых отрезков, кроме нуля и созданы были по принципу «значение цифры соответствует количеству углов в ее написании». Например:ноль-ноль углов, единица-один угол, двойка-два угла и т.д.
2. Брахмагупта-индийский математик, который жил в VII веке первым начал использовать положительные и отрицательные числа.
3. В Американском штате Индиана действует закон: на территории штата число p следует считать равным 4!
Во времена развитого социализма цена продукта практически использовалась как его обозначение. Наиболее популярные газированные напитки (Coca-Cola, Fanta, Sprite) 1 р. 49 коп. (0,5л) и 2 р.87 коп. ( 1л) знал каждый ребенок. Удивительной неожиданностью стало открытие, что первое число, возведенное в степень второго, дает число π. Напомню, что число "пи" является фундаментальной константой, можно даже сказать "константой бытия".
4. Многие представители научного общества называют π математической константой, числом, которое имеет свои секреты и потайные значения. Если посмотреть на ряд исследований, можно сказать, что ученые всех веков и народов уделяли множество времени этому числу, поэтому мы с легкостью смогли выбрать самые интересные факты о числе Pi и представить их в форме текстовой и видео презентации.
Попробуйте ответить правильно на вопросы: