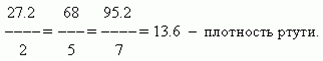Математика: Отношения и пропорции
Впервые интерес к пропорции, возникающей при делении отрезка в крайнем и среднем отношении, возникает в античной науке (Пифагор, Платон, Евклид). Удивительные математические свойства этой пропорции уже тогда создают вокруг нее ореол таинственности и мистического поклонения. Слово «пропорция» ввел в употребление Цицерон в 1 веке до н.э., который буквально означал аналогия, соотношение.
Слово «пропорция» (от латинского propotio) означает «соразмерность», «определённое соотношение частей между собой». В математике: равенство двух отношений. Учение об отношениях и пропорциях особенно успешно развивалось в IV веке до нашей эры в Древней Греции, славившейся произведениями искусства, архитектуры, различными ремеслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Принято считать, что понятие о золотом деление ввел в научный обиход Пифагор, древнегреческий философ и математик. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды, храмов, барельефов, предметов быта и украшений гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создания. Термин золотое сечение ввел Леонардо да Винчи (1452-1519 гг)
Теория отношений и пропорций была подробно изложена в «Началах» Евклида (III век до нашей эры). Оно звучит так: «В верной пропорции произведение крайних членов равно произведению средних».
Благодаря пропорции, по словам Альберти, « тихим и вольным течением взор, точно скользя по карнизам, по простенкам и по всей наружной и внутренней сторонам здания, будет умножать наслаждение новым наслаждением от сходства и несходства».
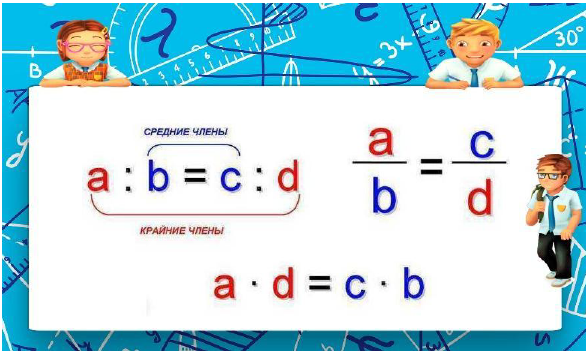
Например, 12 : 20 = 3 : 5; a : b = c : d .
Крайние члены пропорции: 12 и 5 в первой пропорции; a и d – во второй.
Средние члены пропорции: 20 и 3 в первой пропорции; b и с – во второй.
Основное свойство пропорции:
Произведение крайних членов пропорции равно произведению её средних членов.
Две взаимно зависимых величины называются пропорциональными, если отношение их величин сохраняется неизменным. Это постоянное отношение пропорциональных величин называется коэффициентом пропорциональности.
П р и м е р . Масса любого вещества пропорциональна его объёму. Например, 2 литра ртути весят 27.2 кг, 5 литров весят 68 кг, 7 литров весят 95.2 кг. Отношение массы ртути к её объёму ( коэффициент пропорциональности ) будет равно:
Таким образом, коэффициентом пропорциональности в данном примере является плотность.
Пропорцианальность. Это простейший вид функциональной зависимости. Различают прямую пропорциональность. (y = kx) и обратную пропорциональность ( y= k/ x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S = vt ; прямо пропорциональна величина основания y прямоугольника с заданной площадью a обратно пропорциональна высоте x, т. е. y = a/ x.
Свойства прямой пропорциональной зависимости.
1. Каждому значению х соответствует единственное определенное значение у. (первое свойство прямой пропорциональной зависимости) 2. Отношение соответствующих значений величин у и х, связанных прямой пропорциональностью, равно коэффициенту пропорциональности. 3. Если две величины связаны между собой прямой пропорциональной зависимостью, то при увеличении (уменьшении) одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз.
Свойства обратной пропорциональной зависимости.
1. Каждому значению х (за исключением х=0) соответствует вполне определенное значение у. 2. Произведение соответствующих значений х и у равно коэффициенту обратной пропорциональности. 3. Если х увеличивается (уменьшается) в несколько раз, то у уменьшается (увеличивается) во столько же раз, так как их произведение остается неизменным.
Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.
Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длинна всего отрезка так относится к длине его большей части, как длинна большей части к меньшей. Приближенно это отношение равно 0, 618 ≈5/8. Золотое сечение чаще всего применяется в произведениях искусства, архитектуре, встречается и в природе.
Применение «золотого сечения».
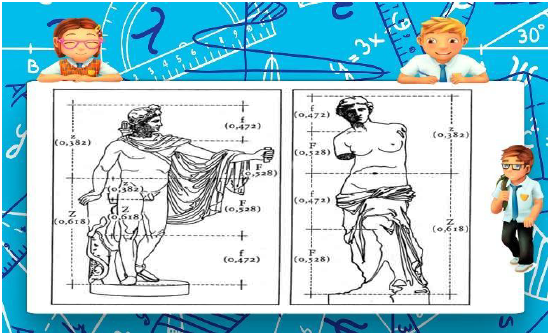
У древних основу составляла теория пропорций. Отношение размеров частей человеческого тела связывалось с формулой «золотого сечения». Скульпторы утверждают, что талия делит человеческое тело (образцом которого является Апполон Бельведерский) в отношении «золотого сечения». а:х=1,618.
Окружающие предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длинны, близкое к 0,618.
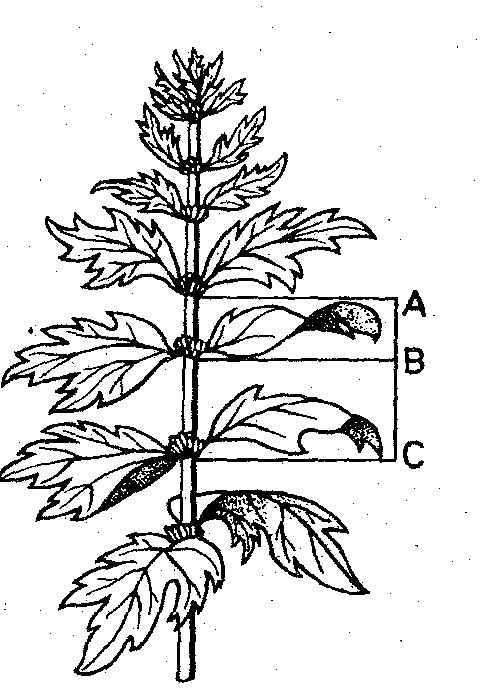
Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В).
Полезные ссылки
В математике отношением называется то частное, которое получается при делении одного числа на другое. Ранее сам этот термин использовался только в тех случаях, когда было необходимо выражение какой-либо одной величины в долях другой, причем такой, которая однородна первой. К примеру, отношения использовались при выражении площади в долях другой площади, длины в долях другой длины и т.п. Решение этой задачи производилось с помощью деления. http://simple-math.ru/arithmetics/ratio-proportion.php
Глоссарий
Отношение – это частное от деления одного числа на другое.
Библиография
- Видеоурок на тему «Прямая и обратная пропорциональные зависимости» http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html
- Видеоурок на тему «Пропорции» http://znaika.ru/catalog/6-klass/matematika/Proportsii.html
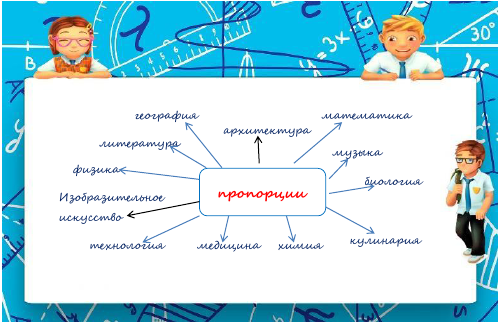
ропорция применяется везде!
Например:
1. Пропорция в физике.
С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т.д. – примеры рычагов. Выигрыш, который дает рычаг в прилагаемом усилии, определяется пропорцией, где M и m – массы грузов, а L и l – «плечи» рычага.
2. Пропорция в географии.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
3. Пропорция в музыке.
Музыкой греки называли ту часть арифметики, в которой говорится об отношениях и пропорциях. Греки создали и научную теорию. Музыки. Они знали: чем «длиннее» натянутая струна, тем «ниже» получается звук, который она издает; что короткая струна издает высокий звук. Однако у музыкального инструмента не одна, а несколько струн, и для того, чтобы все струны при игре звучали «согласно», приятно для уха, длина звучащих частей их должна быть в определенном отношении. Например, чтобы высоты звуков, издаваемых двумя струнами, различались на октаву, нужно, чтобы их длины относились как 1:2. Подобным образом квинте соответствует отношение 2:3, кварте-отношение 3:4 и т.д.
4. Пропорции в архитектуре
Пропорции в архитектуре – это ее внутренняя красота.
ПАРФЕНОН, храм Афины Парфенос на Акрополе в Афинах, памятник древнегреческой высокой классики. Мраморный дорический периптер с ионическим скульптурным фризом (447-438 до н. э., архитекторы Иктин и Калликрат) замечателен величественной красотой форм и пропорций. Статуи фронтонов, рельефы метоп и фриза (окончены в 432 до н. э.) созданы под руководством Фидия. Разрушен в 1687; частично восстановлен. Отношение высоты здания к его длине равно 0, 618.
5. Пропорции в скульптуре.
АПОЛЛОН БЕЛЬВЕДЕРСКИЙ, статуя Аполлона — мраморная римская копия бронзового оригинала работы древнегреческого скульптора Леохара (ок. 330-320 до н. э., Музей Пио-Клементино, Ватикан). Название от ватиканского дворца Бельведер, где выставлена статуя. Долгое время считалась вершиной греческого искусства. На рисунке представлена статуя Аполлона Бельведерского, разделенная в отношении (точка С делит отрезок АD, точка В делит отрезок АС)
Есть у пропорции правило главное
Все его знать и запомнить должны
Средние члены умножишь и крайние
Будут всегда эти числа равны.