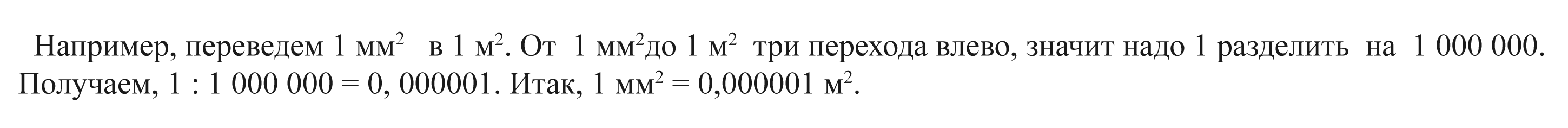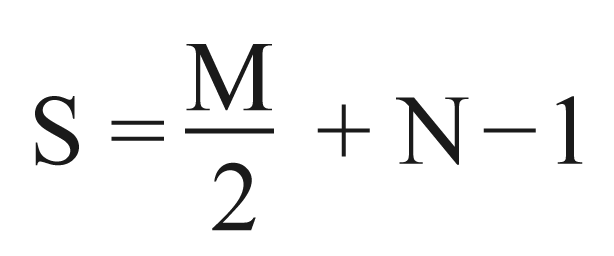Математика: Площадь
Из истории известно, что около четырех тысяч лет назад египтяне умели правильно вычислять площади некоторых прямолинейных фигур, таких, как прямоугольник, квадрат, треугольник и трапеция. Квадрат служил эталоном при измерении площадей благодаря своему совершенному виду. После каждого разлива Нила египтянам заново приходилось разбивать поля на участки, находить их границы. А для этого надо было уметь измерять площади различных фигур: ведь поле может иметь какую угодно форму. Особенно тщательно поля измеряли чиновники фараонов, которые собирали с земледельцев налоги. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку, разделенную метками на локти, ладони и пальцы. Если участок земли квадратный или прямоугольный, то это дело несложное. Надо измерить длину и ширину поля, а потом их перемножить. Например, длина десять локтей, а ширина восемь. Значит, на этом участке можно уложить 80 квадратов со стороной в локоть. Его площадь — восемьдесят квадратных локтей. Но участки могут иметь разную форму. Не всякий участок можно разделить на прямоугольники. А вот на треугольники можно разбить любой участок, — если только он ограничен прямыми линиями. И как следствие, египтяне овладели в совершенстве методами и приемами вычисления площадей различных фигур. Попробуем не отстать от древних жителей долины Нила - разобраться со способом вычисления площадей основных геометрических фигур.
Для начала запомним, площадь – это величина, характеризующая размер геометрической фигуры. Иными словами, это означает, что нужно узнать размер части плоскости, которую занимает данная геометрическая фигура.
До ХVIII века не было единой системы измерения площадей. В каких-то странах длина измерялась в локтях, в каких-то – в ступнях. Так из истории нашей страны известно, что людям часто приходилось измерять площадь юрты (пол юрты), дверей, пахотной земли, пастбищных и сенокосных угодий, таш короо — каменной загородки, чырпык короо— изгороди, сплетенной из облепихи и других кустарников для стоянки овец. Употребляли следующие несложные меры: алакандай — площадь в одну ладонь үйдүн ордундай — площадь под юрту, танап — около 0,005 гектара, теше — площадь одной шестой части гектара.
Согласитесь, зачастую было крайне неудобно так измерять, да к тому же это препятствовало развитию торговли между странами.
Поэтому было принято решение о создание новой общей системы мер, и за эту нелегкую задачу принялись французские ученые. В основу общей системы мер было решено положить единицу длины, которая была бы постоянной «для всех времен и для всех народов». Что же это за длина? Было определено расстояние от полюса земного шара до экватора (заметим, что сделать это было совсем не просто), и это расстояние разделено на 10 000 000. Получившуюся величину и приняли за основную меру длины, и дали ей название – метр, что в переводе с греческого означает «мера». Число 10 стало основанием для подразделений метра, так появились километры, дециметры, сантиметры и миллиметры. Основной единицей измерения площадей стал квадратный метр, кроме которого есть и другие единицы измерения: квадратный километр, гектар, ар (сотка), квадратный дециметр, квадратный сантиметр, квадратный миллиметр.
Расположим единицы измерения площадей в порядке их уменьшения: от квадратного километра к квадратному миллиметру. Между каждыми соседними единицами измерения стоит переводящее число 100, на которое в случае перевода в меньшую единицу измерения надо умножить, а в случае перевода в более крупную - поделить. Если для перевода даны не соседние единицы, а расположенные через одну — надо выполнить два перехода. Через три — три перехода. В этом случае переводящее число будет составлено путем совмещения единицы и всех нулей, которые мы встречаем по дороге. При движении влево (то есть при переводе в БОЛЕЕ КРУПНУЮ единицу) мы делим, а при движении вправо (то есть при переводе в МЕЛКУЮ) — умножаем.
Чтобы запомнить, соотношение между единицами площади, предлагаем памятку. Ее можно распечатать и использовать при приготовлении домашнего задания. Конечно, будет очень хорошо, если вы запомните, как выполнять перевод из одной единицы измерения в другую.
Уже в древнем Вавилоне умели вычислять площадь прямоугольника, а древние египтяне использовали почти такие же методы вычисления площадей различных фигур (но далеко не всех, и с небольшими погрешностями), как и мы с вами. А самый известный древнегреческий математик Евклид (который жил около 300 г. до н.э.) в своем многотомном труде «Начала» (10 из 13 книг посвящены геометрии) описывает достаточно большое количество способов нахождения площадей многих геометрических фигур. Первые рукописи, которые содержат геометрические сведения на Руси (правда, только практического характера), датируются XVI веком. В них собраны правила измерения площадей фигур разных форм.
Современная математика шагнула далеко вперед, и сейчас с большой точностью можно найти площадь всевозможных фигур, а даже тех, которые ограничены не прямыми линиями. Но мы только познакомимся с формулами площадей основных геометрических фигур: треугольника, прямоугольника, квадрата, параллелограмма, ромба, трапеции и круга. Объяснение, что это за фигуры, можно найти в нашем глоссарии. А сами формулы - специально для вас разместили все формулы в удобную таблицу. Распечатайте, выучите и применяйте!
Что делать, если ...
Что делать, когда дан многоугольник, у которого пять и более углов? Конечно, можно применить его разделение на более простые составляющие фигуры — прямоугольники, треугольники, трапеции, параллелограммы, нахождение площади которых хорошо известно. Любопытное свойство многоугольников было обнаружено австрийским математиком Георгом Пиком. Он обнаружил, что многоугольник вершины которого располагаются в узлах квадратной сетки могут быть найдены по формуле:
где S — площадь многоугольника;
N — количество узлов сетки, расположенных внутри многоугольника;
M — количество узлов сетки, попадающих на стороны многоугольника и на его вершины.
Под «узлами» имеется ввиду пересечение линий.
В примере 1.1 площадь нашего четырехугольника ABCD также равна 24,5. Отсюда делаем вывод, что формула Пика дает верный результат. Помимо этого, она имеет ряд преимуществ перед другими способами вычисления площадей многоугольников на клетчатой бумаге:
- для вычисления площади многоугольника, нужно знать всего одну формулу
- формула Пика очень проста для запоминания. Очень удобна и проста в применении. А многоугольник, площадь которого необходимо вычислить, может быть любой, даже самой причудливой формы.
Глоссарий
Прямоугольник — четырехугольник, у которого все углы прямые (равны 90 градусам).
Квадрат — четырёхугольник, у которого все углы и стороны равны.
Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны параллельны, то есть лежат на параллельных прямых.
Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны.
Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, трапеза») — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие не параллельны. Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон.
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла.
Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть 90 градусов).
Круг — геометрическое место точек плоскости (всех таких точек), расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.
Радиус — отрезок, соединяющий центр круга с его границей.
Диаметр — отрезок, соединяющий две точки границы круга и содержащий его центр.
Круговой сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Полезные ссылки
Аргументы в пользу решения задач
Человеческий мозг устроен так, что он работает всегда и его нельзя занимать скучной и бесполезной работой, его необходимо загружать красивыми и интересными задачами. Вы спросите, почему? Ответ прост. Решая задачи, мы учимся анализировать свои возможности, развиваем умение находить не один, а несколько вариантов решения и наконец, прийти к результату кратчайшим путем.
Если вы всегда с завистью смотрели на одноклассников, которые с легкостью решали сложные задачи и участвовали в математических олимпиадах, то этот конкурс-игра для вас. Каждый может проверить себя в способности сосредотачиваться, логически мыслить, быть организованными и настойчивыми. https://nic-snail.ru
Большинству школьников не надо объяснять, что такое «Кенгуру», — это международный математический конкурс-игра под девизом «Математика для всех». Главная цель конкурса — привлечь как можно больше ребят к решению математических задач, показать каждому школьнику, что обдумывание задачи может быть делом живым, увлекательным, и даже веселым! http://mathkang.ru/
А можно не только проверить свои знания, но и попробовать себя в качестве учителя - создать свои тесты! Вы сами выбираете типы заданий и уровни сложности. Данные тесты могут работать не только через Интернет. Точно так же их можно использовать без доступа к интернету. На любом устройстве и под любой операционной системой. Попробуйте и оцените все преимущества! http://testedu.ru/test/matematika/
Библиография
- В.А. Гусев, А.Г. Мордкович Математика. Справочные материалы М.: Просвещение, 1988.
- Депман И.Я. Из истории математики. Либроком, 2010. – 152с.
- Федин С. Н. Математики тоже шутят. — 4-е изд. — М.: УРСС, 2012. — 216 с.
- Системы измерения и счет у кыргызов.: [Электронный ресурс] //Open.kg Открытый Кыргызстан. URL: https://www.open.kg/about-kyrgyzstan/culture/ethnography/1970-sistemy-izmereniya-i-schet-u-kyrgyzov.html . (дата обращения: 20.11.2017)
- Центр «Снейл» - Массовые дистанционные образовательные конкурсы для детей и педагогов. : [Электронный ресурс] // Центр «Снейл» , 2005-2017.URL: https://nic-snail.ru/ (дата обращения: 20. 11. 2017)
- Международного математический конкурс «Кенгуру». : [Электронный ресурс] // Кенгуру 1995-2017. URL: http://mathkang.ru/ (дата обращения: 20. 11. 2017)
- Проект «Образовательные тесты». : [Электронный ресурс] // TestEdu.ru 2013-2017. URL: http://testedu.ru (дата обращения: 20. 11. 2017)
- Как найти площадь прямоугольника? : [Электронный ресурс] // КакИменно.ру, 2017. URL: http://kakimenno.ru/raznoe/95-kak-nayti-ploschad-pryamougolnika.html (дата обращения: 20. 11. 2017)
- Формула Пика. Статья Александра Крутицких. : [Электронный ресурс] // Проект "Математика? Легко!!!". URL: https://matematikalegko.ru/formuli/ploshhad-figury-na-liste-v-kletku-formula-pika.html (дата обращения: 20. 11. 2017)
- Прямоугольник [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88080404, сохранённая в 14:34 UTC 3 октября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Прямоугольник (дата обращения: 20. 11. 2017)
- Квадрат [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88889010, сохранённая в 14:47 UTC 9 ноября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: http://ru.wikipedia.org/?oldid=88889010 (дата обращения: 20. 11. 2017)
- Параллелограмм [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88559185, сохранённая в 17:11 UTC 25 октября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: http://ru.wikipedia.org/?oldid=88559185 (дата обращения: 20. 11. 2017)
- Ромб : Материал из Википедии — свободной энциклопедии : Версия 88808560, сохранённая в 13:58 UTC 5 ноября 2017 // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Ромб (дата обращения: 20. 11. 2017)
- Трапеция [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 89051983, сохранённая в 22:06 UTC 17 ноября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Трапеция (дата обращения: 20. 11. 2017)
- Треугольник [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 89060175, сохранённая в 11:07 UTC 18 ноября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Треугольник (дата обращения: 20. 11. 2017)
- Прямоугольный треугольник [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88835246, сохранённая в 17:10 UTC 6 ноября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Прямоугольный_треугольник (дата обращения: 20. 11. 2017)
- Круг [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88288149, сохранённая в 07:07 UTC 13 октября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Круг (дата обращения: 20. 11. 2017)
- Сектор (геометрия) [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 83986175, сохранённая в 03:09 UTC 1 марта 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Сектор_(геометрия) (дата обращения: 20. 11. 2017)
- Герон [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88623529, сохранённая в 22:00 UTC 27 октября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Герон (дата обращения: 20. 11. 2017)
- Пик, Георг [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88102327, сохранённая в 08:49 UTC 4 октября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Пик,_Георг (дата обращения: 20. 11. 2017)
звестно, что площадь измеряется в квадратных единицах. Они будут различными в зависимости от размера измеряемой площади. Конечно, можно измерять все в одних единицах, но в результате мы будем получать либо слишком маленькие, либо слишком большие для восприятия цифры.
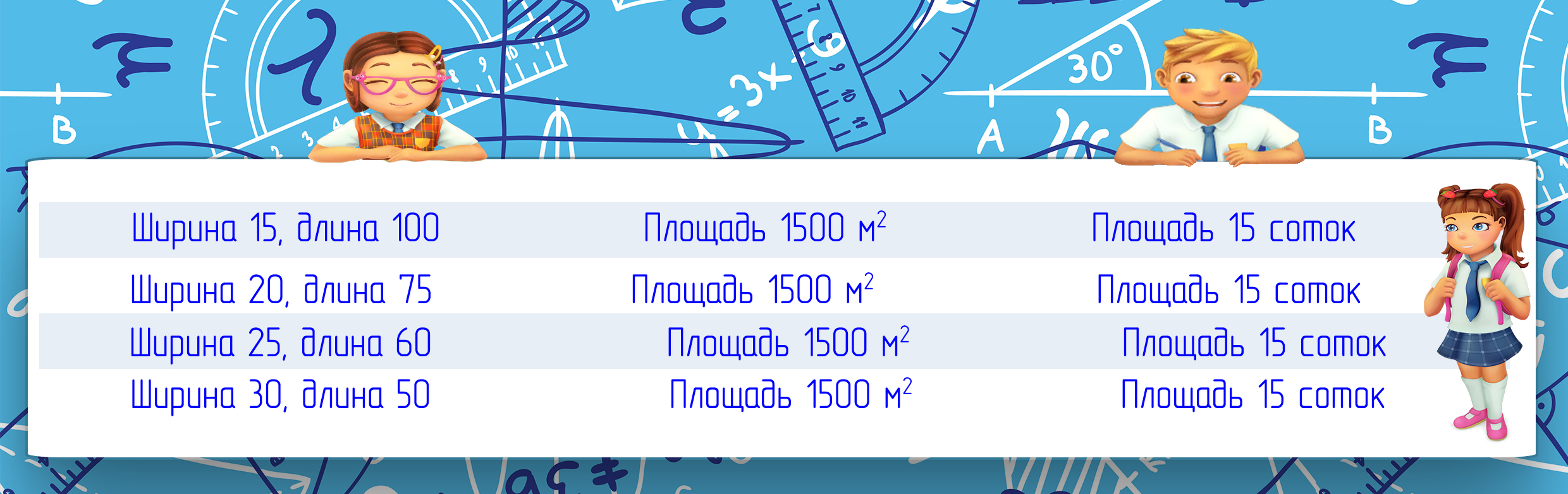
Площадь земельных участков очень часто указывают в сотках. Одна сотка — это площадь участка размером 10 метров на 10 метров, которая составляет 100 квадратных метров и поэтому называется соткой. Вот несколько характерных примеров размеров, которые может иметь земельный участок.
В будущем, если вы вдруг забудете, как найти площадь прямоугольника, то вспоминайте очень старый анекдот, когда дедушка спрашивает у пятиклассника как найти площадь Ала-Тоо, а тот отвечает, что нужно ширину Ала-Тоо умножить на длину Ала-Тоо.
Математика появилась одновременно со стремлением человека изучить мир вокруг себя. Изначально она входила в состав философии и не была выделена как отдельная дисциплина наравне с той же астрономией, физикой. Однако с течением времени ситуация изменилась. Знаний у людей накапливалось все больше, в итоге произошло разделение точных и естественных наук. После официального "рождения" каждая из них пошла своим путем, развиваясь, укрепляя фундамент теорией, подкрепленной практикой. Казалось бы, какая практика может быть у математики, самой абстрактной из наук? Этот предмет способен описать абсолютно все процессы, происходящие на нашей планете и за ее пределами, а знание природы явления позволяет делать выводы и строить прогнозы. Отсюда можно сделать вывод, что все науки связаны между собой, наиболее очевидна эта зависимость между математикой и физикой. Поэтому в большинстве случаев великие математики и физики составляют одну группу ученых. Посудите сами, как можно описать что-то, не получив при этом обоснования? Человеческая история - это не только покорение новых территорий и войны, в которых сильные мира сего преследуют в первую очередь свои интересы, но и бесконечные научные выкладки, призванные объяснить, показать, познать и выяснить перспективу завтрашнего дня. Кто они, великие математики прошлого, что подготовили почву для современных открытий? Знакомьтесь!
А знаете ли вы, что, зная только формулу площади прямоугольника, можно запросто находить площади таких фигур как параллелограмм, ромб, трапеция и треугольник? Нет? Тогда чтобы убедиться в этом, посмотрим видеоролик «Площадь фигур».
Как-то так сложилось, что мы традиционно представляем себе математиков занудными сухарями или далекими от реальности рассеянными чудаками. В обоих этих случаях сама мысль о каком бы то ни было юморе кажется абсурдной. Да и вообще, само сочетание «математика и юмор» кажется фантастикой. Однако, это далеко не так, и в действительности математических шуток даже больше, чем вы можете предположить. И более того, именно математический юмор является наиболее утонченным и разнообразным.