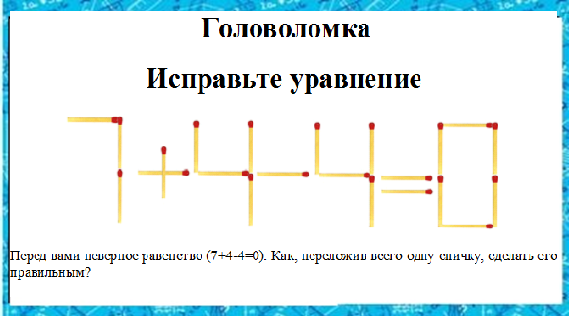
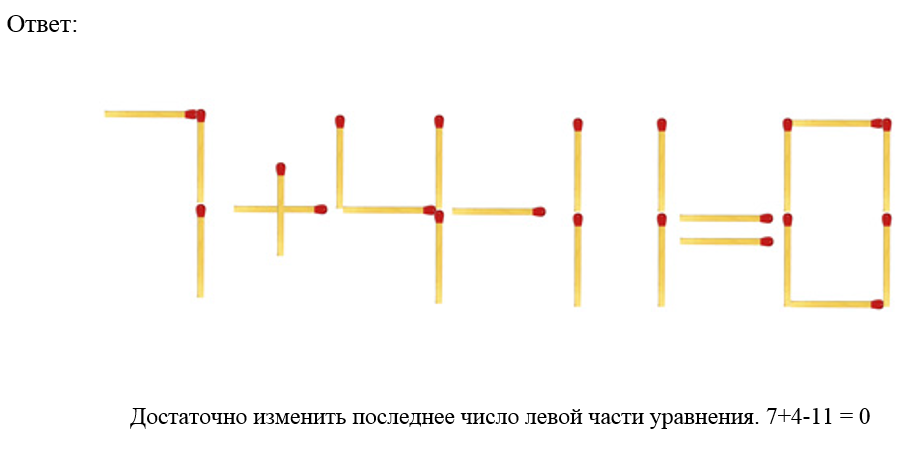
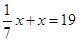Математика: Решение уравнений
Еще в глубокой древности в математических сочинениях встречались уравнения, а также задачи, решаемые с помощью уравнений. Так, в египетском папирусе около 2000 лет до нашей эры (причем, как указывает в нем автор, писец Ахмес, это математическое сочинение является копией с другого, более древнего сочинения) имелись задачи на отыскание неизвестного числа. Это неизвестное называлось «хау» (куча) и обозначалось особым иероглифом.
Вот примеры задач из этого папируса.
1) «Неизвестное, его седьмая часть, его целое составляет 19».
В современном виде задача запишется так:
2) «
сложено и 
отнята: остаток 10».
В папирусе решению, задачу следует понимать так: к неизвестному прибавлено его и отнята полученной суммы; остаток 10; найти число.
Задача в современном виде запишется так: 
; Ответ: х=9
3) У Диофанта также встречаются уравнения с одним неизвестным, например:
«Числа 20 и 100. Нужно одно и то же число прибавить к меньшему и вычесть из большего; отношение суммы к разности равно 4».
Задача приводит к уравнению: 
4) В индийской рукописной арифметике VII и VIII века нашей эры, являющейся копией с более древней рукописи (III-IV века), имеется такая задача: «Из четырех жертвователей второй дал вдвое больше первого, третий втрое больше второго, четвертый вчетверо больше третьего, а все вместе дали 132. Сколько дал первый?» Получаем уравнение: В рукописи задача решается способом «ложного положения». (Этим способом пользовался и Л.Ф. Магницкий в своей «Арифметике».) «Если бы первый дал 1, то второй бы 2, третий 6, четвертый 24, а все вместе 33. Но всего было 132, то есть вчетверо больше. Значит, и каждый из жертвователей дал вчетверо больше». Ответ: 4; 8; 24; 96.
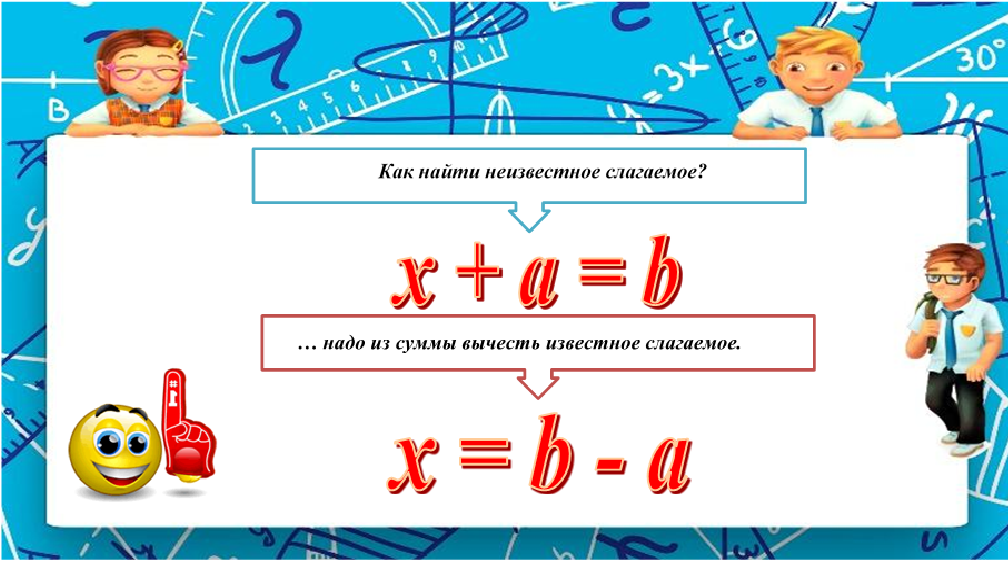
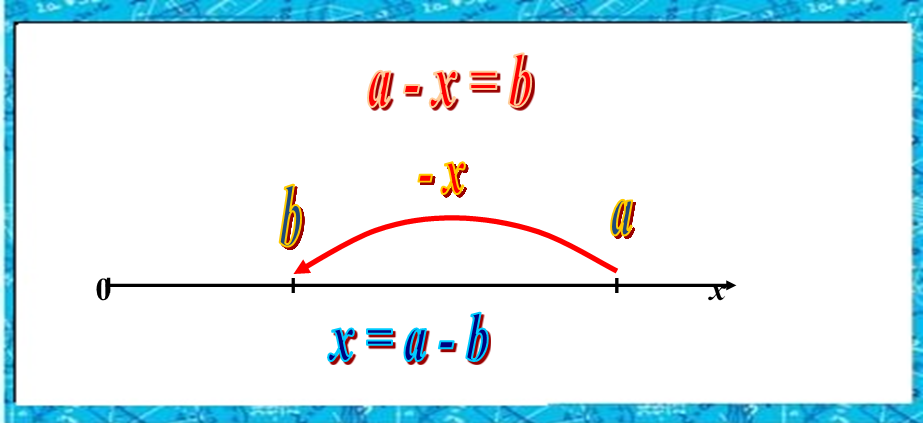
Но общее правило для решения уравнений первой степени с одним неизвестным дал в IX веке Мухаммед аль-Хорезми. В своем сочинении «Аль-джебр и аль-мукабала» он дает два приема, применяемых при решении уравнений.
1) Прием «аль-джебр» заключается в том, что если имеются в уравнении отрицательные (вычитаемые) члены, то следует прибавить противоположные им члены к обеим частям уравнения, и тогда все члены будут положительными.
2) Прием «аль-мукабала» заключается в вычитании из обеих частей уравнения одинаковых членов, что приводит к его упрощению.
Например, дано уравнение: 5х-17=2х-5 Применим «аль-джебр»: прибавляем к каждой части уравнения 5 и 17. Получим: 5х+5=2х+17 Применим «аль-мукабала»: вычитаем из каждой части 2x и 5. Получим: 3х=12 Отсюда легко находится х.
Решим уравнение:
Полезные ссылки
Первоначальные способы решения уравнений были достаточно сложными и разнообразными. В процессе развития математики произошло их значительное упрощение, и для каждого типа уравнений появился единый алгоритм решения. Более подробно можете увидеть: https://www.youtube.com/watch?v=WpwOQHVB5s4
Глоссарий
Переменные - атрибут системы, который меняет свое значение. Они обозначаются буквами, например, х, а, b, с...
Библиография
- Видеоурок на тему «Решение уравнений. https://www.youtube.com/watch?v=Nwe2UqXONJ4
- Видеоурок на тему «Решение уравнений» https://www.youtube.com/watch?v=PI8VHwDgkXc
- Шутки и загадки http://gadaika.ru/shutki/v-kantselyarskom-magazine
Математика – как высокая винтовая лестница,
чтобы взойти по ней к вершинам знаний,
надо пройти каждую ступеньку от первой до последней.
РЕШАЕМ УРАВНЕНИЯ НА ANDROID ЗА 1 СЕКУНДУ!
Школьник зашел в лавочку возле школы. На прилавке лежали ручки по 30 рублей за штуку и карандаши по 15 рублей. Мальчик приобрел один карандаш и пошел к выходу, но по дороге подумал: «Я уже отдал продавцу 15 рублей, значит, если вернуть покупку, в сумме на моем счету окажется 30 руб». Сможет ли школьник теперь купить ручку? Почему?
Ответ
Не сможет.
В качестве объяснения приведем небольшую шутку.
Студент заказал в кафе булочку, но затем решил, что не слишком голоден и обменял ее на чашечку кофе. Выпив напиток, он направился к выходу, не расплатившись. Cамо собой, за ним побежала буфетчица.
- Вы не заплатили за кофе!
- Да, все верно, но я же взял его взамен булочки!
- Так булка тоже не оплачена!
- Верно, но я ведь ее и не ел!
Ответ
Ответ
