БИЛИМ БУЛАГЫ

Натуралдык сандардан башка дагы бөлчөктүк сандар бар. Бөлчөктүк сандар же бөлчөктөр натуралдык сандарды тең бөлүккө бөлүүдө алынат: экиге, үчкө, бешке жана андан чоңдорго. Бөлүктөр кээ бирде, бир чоңдукту бүтүн сандар менен ченөө мүмкүн эмес болгон убактарда колдонулат. Мисалы: адамдын боюн бүтүн сан (метр) менен ченеш мүмкүн эмес.

Адамдар күн сайын бир бүтүндү бөлүктөргө бөлөт, аларды бөлүктөр деп аташат. Көбүнчө жарым көп колдонулат- жарым күн, жарым саат, жарым кило. Ошондой эле башка дагы бөлчөктөр колдонулат- үчтүк, чейрек, ондук, жүздүк. Бөлүктөр бир бүтүн нерсени бирдей бөлүккө бөлүүдөн пайда болот (нанды, кагазды) же ченөө бирдиктеринде (саат, киллограмм). Бөлүк ар бир барабар бирдиктин бөлүмү. Бөлүктөр канча бирдей бөлүккө бөлүнгөнүнө жараша аталат. Эки бөлүккө бөлүнгөндө “жарымы” деп аталат, ал эми үчкө бөлүнсө үчтүн бири, төрткө- чейрек. 5 ке 6 га 7 ге бөлүнгөндө бештин, алтынын, жетинин бир бөлүгү делинет. Ошондой эле жарымы үчтөн бири төрттөн биринин оордуна экинчи, үчүнчү, төртүнчү үлүшү аталыштары колдонулат. Мисалы үчүнчү, жыйырманчы, жетимиш үчүнчү бөлүктөрү: , , , деп жазылат, үчтүн бири, жыйырманын бири, жетимиш үчтүн бири болуп окулат. Эгерде бирдикти бирдей n бөлүккө бөлсөк, анда болуп жазылып, эндин бир бөлүгү болуп окулат.

Математиканын биринчи китептеринде (VII к) бөлчөктөрдү бөлүмү деп аташкан, кийинчерээк “бөлүнгөн сандар” делинген. Орус тилинде бөлчөк сөзү VIII кылымда пайда болгон, ал “бөлүү”- бөлүктөргө сындыруу, талкалоо этишинен алынган. Сандардын бөлүктөрү же алардын суммаларын Бөлчөк сандар деп аташат. Бөлчөк сандар үчүн бөлчөктүн аталыштары колдонулат. Эски жетектөөчү китебинде Русьтагы бөлчөктөрдүн кийинки аталыштары берилген: жарым, үчтөн бир, үчтүн жарымы, төрттүн жарымы, үчтүн жарымынын жарымы, төрттүн жарымынын жарымы, үчтүн жарымынын жарымынын жарымы, (үчтүн кичинеси).

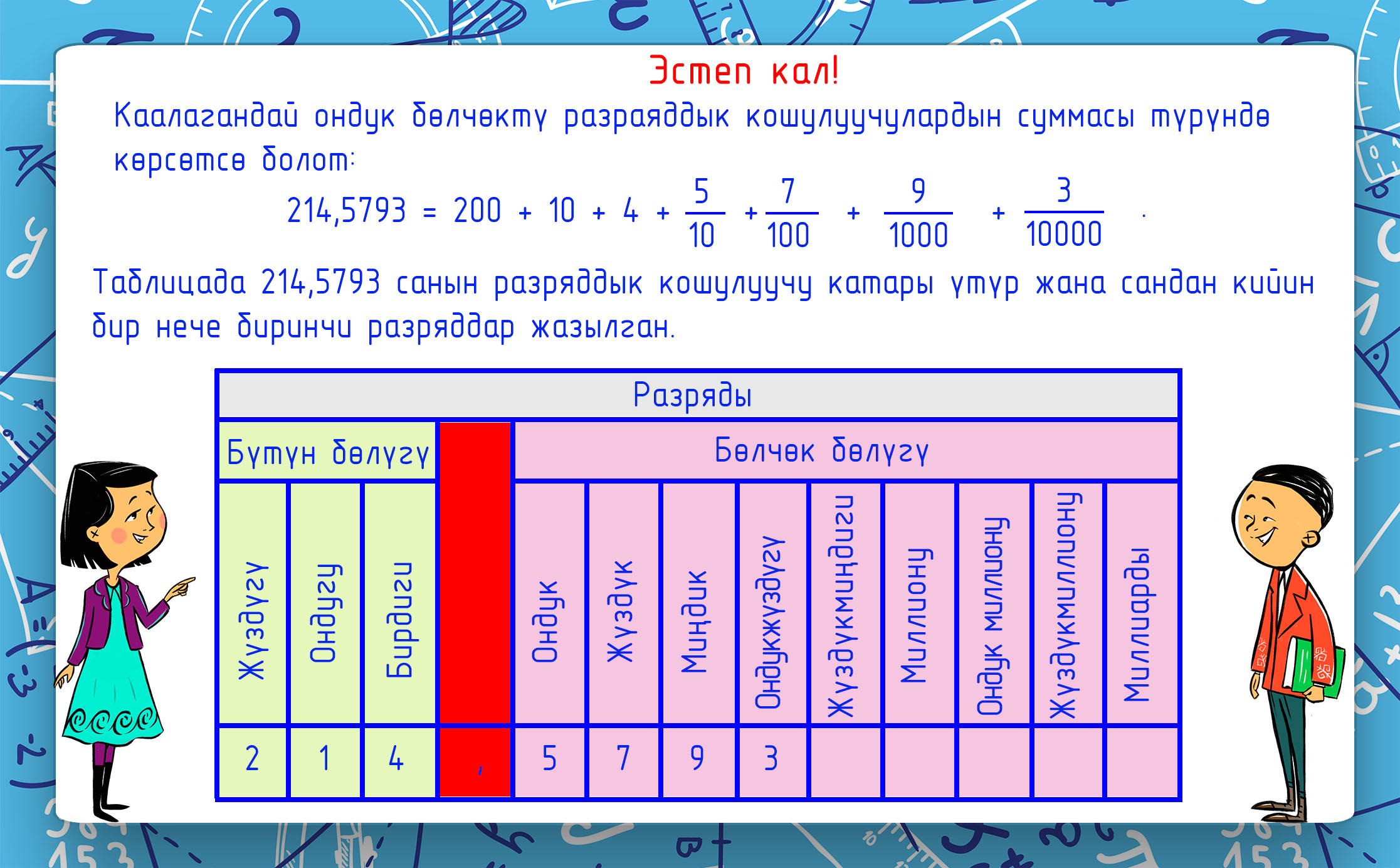
Биздин күндөргө чейин кандай аталыштагы бөлчөктөрдүн жеткенин билүү үчүн видео сюжет көрүүгө чакырабыз. Жөнөкөй эле бөлчөктү жазуу үчүн эки натуралдык сан жана бөлчөк сызыгы керектелет. Бөлчөк сызыгынын астына бөлчөктүн бөлүмү жазылат, ал болсо бөлчөк кайсы бөлүктөн тураарын көрсөтөт. Сызыктын үстүнө алымы жазылат, ал бөлчөк канча бөлүмдүн суммасынан тураарын көрсөтөт. Көбүнчө ондук номерлөө колдонулат. Номерлөөнүн аталышы кийинки эрежеден чыккан: ар бир бирдиктин разряды мурунку разряддын бирдигинен 10 эсеге чоң. Бирдиктин разряды натуралдык сандарды жазууда эң кичинеси болуп эсептелет. Мурунку кичине разряддын бирдиги ар бир разряддын бирдигинен 10 эсе кичине болушу керек. Онунчу бөлүктүн бирдигинин разряды оңураак жайгашат жана үтүрдүн разрядынын бирдигин бөлүп турат.

Мисалы, санын 13,4 деп жазсак болот ал эми 2,8 деп жазылат.

Үтүрдүн оң жагындагы разряддар андан ары уланышы мүмкүн жанан алар үчүн атайын эреже бар: ар бир разряддын бирдиги мурдакы разряддын бирдигинен 10 эсеге кичине. Үтүрдөн кийинки биринчи разряд ондук бөлчөк деп аталат. Үтүрдөн кийинки экинчи разряд жүздүк бөлчөк, үтүрдөн кийинки үчүнчү разряд миңдик бөлчөк болот. Сандардын жана үтүрдүн жардамы менен жазылган бөлчөктөр ондук бөлчөктөр деп аталышат, ал эми бөлчөктүн сызыгынын жардамы менен жазылган бөлчөк кадимки бөлчөк деп аталат.

Жөнөкөй бөлчөктүн ондук түрүн жазуу үчүн алымды бөлүмгө бөлүү керек.

Башталышына

Бөлчөктөр жөнүндө

Баардык бөлчөктөр жөнүндөгү чындык “Бөлчөктөр каякта колдонулат ” деген видео жүгүртмөдө, аны көрүү менен силер бөлчөктөрдү акча санаш үчүн ойлоп тапкандарын билесиңер. Көрөлү:

Башталышына

Математикалык жат жазуу

Математикалык жат жазуу баарына белгилүү. Бирок көбүбүз билимибиздин мындай формада текшерилишин каалабайбыз. Антпешибиз керек! Математикалык жат жазууларды убак-убагы менен жазып турууда сиз тапшырманы угуп кабыл алганга үйрөнөсүз, а бул болсо лекцияны угууну үйрөнүүгө, мугалимдин сөзү, досторуңдун сөзү деги жалпы угууңузду жакшыртат. Баардык биздин карамагыбыздагы маалымат каналдарынын ичинен угуу каналы көрүүдөн кийинки экинчи ардактуу оорунду ээлейт. Анын мүмкүнчүлүктөрүн өнүктүрүү- өтө маанилүү. Ошондуктан өзүңөрдүн күчүңөрдү сынап көргүлө демекчибиз. Тапшырмаларды аткарууга, суроо жоопторун жүктөөгө жана чыгарып алууга болот.

• 
• 
• 
• 

Башталышына

Глоссарий

Натуралдык сандар - бул сандар, предметтерди саноо үчүн же бирдей предметтер арасындагы тигил же бул предметтин катар номерин көрсөтүү үчүн колдонулат.

Марк Ту́ллий Цицеро́н - (лат. Marcus Tullius Cicerō; б.з.ч. 106 – б.з.ч. 43) — байыркы римдик саясий ишмер, оратор жана философ.

Асс (эскирген «ас», лат. as, assarius) —уламыш боюнча Сервия Туллиянын убактсында, бирок –Республика болгон доор мезгилинде гана, биринчилерден пайда болгон байыркы римдин коло тыйынынын аталышы.

Башталышына

Пайдалуу шилтемелер

1. Бөлчөктөрдүн тарыхы бир миң жылдыкка эсептелбейт. Бир бүтүндү бир нече бөлүккө бөлүү байыркы Египеттин жана Вавилондун аймагында башталган. Жылдар өткөн сайын бөлчөктөр менен жасалуучу операциялар кыйындай баштаган, аларды жазуунун формалары дагы алмашкан. Математиканын бул бөлүмүнүн өз ара мамилелеринде Байыркы мамлекеттердин ар биринин өздөрүнүн өзгөчөлүктөрү болгон. [Электрондук ресурс] // «ФБ», 2017 URL: http://fb.ru/article/236507/drobi-istoriya-drobey-istoriya-vozniknoveniya-obyiknovennyih-drobey (кайрылуу датасы: 20. 11. 2017)

2.Азия менен Европанын математиктери ондук бөлчөккө ар кандай убакытта келишти. Азиядагы ондук бөлчөктүн жаралышы жана өнүгүшү метерология (ченөө илими) менен тыгыз байланышта болгон. Биздин заманга чейин II кылымда эле узундукту ондук система менен ченөө бар болчу. Кызыкпы? Анда кененирээк бул жакта: [Электрондук ресурс] // Google 1999 – 2017 URL:http://matemdp84.blogspot.ru/2013/02/blog-post_8.html (кайрылуу датасы: 20. 11. 2017)

Башталышына

Библиография

• Бөлчөк сандар: [Электрондук ресурс]//Avtor24,2017URL: https://author24.ru/spravochniki/matematika/ drobnye_chisla/ (кайрылуу датасы 20.11.2017)
• Бөлчөктөр: бөлчөктөрдүн тарыхы. Кадимки бөлчөктөрдүн жаралыш тарыхы.: [Электрондук ресурс]// “ФБ”.2017URL http://fb.ru/ article/236507/drobi-istoriya-drobey-istoriea-vozniknoveniya-obyiknovennyih-drobey. (кайрылуу датасы 20.11.2017)
• Жеке бөлчөктөрдүн аталышы. “Бөлчөктөр кайда колдонулат” Видео [Электрондук ресурс]// Zero to Hero YouTube,2017 URL:http://www. youtube.com/ watch?v=y75kalTzSKo (кайрылуу датасы 20.11.2017)
• Кызыктуу математика. Ондук бөлчөктөр. URL: [Электрондук ресурс]// Google 1999- 2017 URL:http://matemdp84/blogspot.ru/2013/02/blog-post_8.html ( кайрылуу датасы 20.11.2017)

Башталышына

Бөлчөктүн доорунан

А

Азыркы бөлчөктөрдү жазуу системасы бөлүмү жана алымы менен Индияда түзүлгөн.

Индиялыктар кадимки бөлчөктөрдү пайдаланышкан.

Кадимки бөлчөктөрдү бөлүмү жана алымынын жардамы менен белгилөө Индияда б.з.ч. VIII кылымда эле кабыл алынган, бирок, бөлчөк белгиси жок эле. Айырмачылыгы бөлчөктүн бөлүмү үстүнө, ал эми алымы болсо – астына жазылган. Бөлчөктүн азыркы жазылышы арабдар тарабынан колдонуп башталган. Вавилондо он алтымыштык бөлчөктөр колдонулган. Бөлчөктүн бөлүмү 60, 602, 603 ж.б. болгон. Бирок бардыгы алтымыштык бөлүкчөлөргө так бөлүнгөн эмес. Мисалы, жетинин бир бөлүгүн жакындатып кана эсептесе болот. Алтымыштык бөлүкчөлөрдү грек жана араб математиктери жана астрономдору пайдаланышкан. Бирок натуралдык сандар менен гана, анткени ондук жана алтымышынчы система менен иштөө абдан ыңгайсыз болгон, ошондой эле жөнөкөй бөлчөктөр менен иштөө дагы кыйын болгон. Голландиялык математик Симон Стевин Ондук бөлчөктөр менен иштөөнү сунуштаган. Биринчи алардын жазуулары аябай татаал болгон, бирок анын негизинде азыркы заманбап жазуулар пайда болгон. Азыркы комьпютердик техникаларда Русьта пайдаланылган экилик бөлчөктөр пайдаланылат: жарым, төрттүк, төрттүктүн жарымы, төрттүктүн жарымынын жарымы.

Байыркы Римде болсо бөлчөктүн он экилик системасы пайдаланылган. Кийинчерээк коло тыйындын салмагынын бирдиги- асс-12 бирдей бөлүккө бөлүнгөн-унций. 12инин бир бөлүгү асс унция деп аталат. Жол, убакыт жана башка чоңдуктарды салмак менен салыштырышкан. Мисалы,Римдиктер 7 унций жол жүрдүк же болбосо 5 унций китеп окудук дешкен, бул болсо он экинин жетисин жол басканын жана он экинин беши окулган китеп болгон. Он эки бирдей бөлүктөн дагы майдараак бөлчөктөр болгон. Мисалы, “скурпулезно” сөзүнүн чыгышы римдик 1/288 асса- скрупулус аталышынан чыккан. Ошондой эле “семис”- ассанын жарымы, “сектанс”-алтынчы бөлүк, “семиунция”жарым унция (1/24 асса) лар колдонулган. Баардыгы 18 ар кандай аталыштагы бөлчөктөр пайдаланылган. Бөлчөктөр менен иштөөдө алардын кошуу жана көбөйтүү таблицаларын эске тутуу, билүү керек эле. Мисалы, Римдик сатуучулар триенсти (1/3 асса) жана секстантаны кошууда семис болоорун толук билишчү, ал эми бесаны (2/3 асса) сескунцияга (32 унций же 1/8 асса) көбөйткөңдө унция келип чыгат. Эсепти жеңилдетиш үчүн атайын таблицаларды түзүшкөн алардын кээ бирлери биздин күндөргө чейин жетти. Он экилик системада бөлүмдөрү 10 же 100 болгон эмес, ошондуктан римдиктерге 10 го жана 100 гө бөлүү кыйын болгон. 1001 ассаны 100 бөлүүдө бир римдик математик биринчи 10 ассаны алган, андан кийин ассты унцийге бөлгөн ж.б.у.с. Бирок калдыктан кутула албай койгон. Ушундай эсептер менен иштебеш үчүн римдиктер процентти пайдаланып башташкан. Алар карыз кишиден лихва (карызга алган акчадан сырткары үстүк акчанын алынышы) алышкан. Алып жатышып: “лихва карызга алган сумманын 16 жүзүн түзөт”, “ар бир 100 сестерциев карызга 16 сестерциев лихва төлөйсүң” деп айтышкан. Ошентип “жүзгө” деген сөз латынча “про центум” делинген, ошондуктан жүзүнчү бөлүк процент деп аталган.

Жөнөкөй бөлчөктүн түрүн кантип аныктоого болот

Кадимки бөлчөктөрдү окуп үйрөнүүдө кайсы бөлчөк туура экендигин, кайсынысы туура эмес эстеп калуу кыйын, бөлүм менен алым кандай оорундарды ээлейт.