БИЛИМ БУЛАГЫ

История возникновения координат на плоскости

История возникновения координат и системы координат начинается очень давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Древнегреческого ученого Анаксимандра Милетского (ок. 610-546 до н. э.) считают составителем первой географической карты. Он четко описывал широту и долготу места, используя прямоугольные проекции.

Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.

Идея изображать числа в виде точек, а точкам давать числовые обозначения зародилась в далекой древности. Первоначальное применение координат связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта.

Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту. До наших времён дошла такая история, которая подтолкнула его к открытию. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650)– того самого, чьим именем названы прямоугольные координаты. Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.

Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Кроме того, в своей работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. «Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

А вот термины «абсцисса», «ордината» и «координаты» были впервые введены Вильгельмом Лейбницем в семнадцатом веке.

Проведем две перпендикулярные координатные прямые — и , которые пересекаются в начале отсчета — точке О. Эти прямые называют системой координат на плоскости, а точку О —началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.

Пусть -некоторая точка плоскости. Проведем через нее прямую , перпендикулярную координатной прямой , и прямую перпендикулярную координатной прямой . Так как точка A имеет координату 4, а точка координату 3 , то положение точки определяется парой чисел (4, 3) . Эту пару чисел называют координатами точки M . Число 4 называют абсциссой точки , а число 3 — ординатой точки . Координатную прямую X называют осью абсцисс, а координатную прямую — осью ординат. Точку с абсциссой 4 и ординатой 3 обозначают так: (4, 3). На первом месте пишут абсциссу точки, а на втором ее ординату. Если переставить координаты местами, то получится другая точка (3, 4) , которая тоже изображена на рисунке. Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината, и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами. Для того, чтобы нанести точки на координатную плоскость, Вы должны понимать организацию координатной плоскости и знать, что делать с координатами (х,у) https://www.youtube.com/watch?v=aOhVGfdRtgU . Пример. Выберите точку, изображенную на координатной плоскости.

Плоскость в жизни

Как по вашему, может ли пригодиться в повседневной жизни знания о координатной плоскости? И доводилось ли вам слышать такую фразу, как «оставьте свои координаты» или «по каким координатам вас можно найти»? И задумывались ли вы над тем, что может обозначать эти выражения?

Оказывается все очень просто и банально и это значит местонахождение того или иного объекта, по которому легко найти человека или какое-то определенное место. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно.

Такой системой координат может быть как домашний адрес, так и номер телефона, место работы и т.д.

Ведь даже при покупке билетов на поезд, вы знаете не только его номер и место назначения, но и обязательно должен быть указан номер вагона и места.

Чтобы найти свое место в зале, сначала мы ищем свой ряд, затем свое место.

Чтобы пойти в гости к однокласснику, недостаточно знать только дом, в котором он живет, а нужно еще и знать номер квартиры.

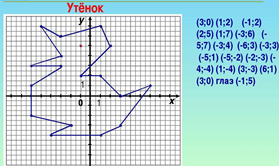
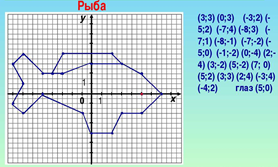
Рисуем по координатам

Суть задания заключается в том, чтобы по заданным координатам точек построить на координатной плос¬кости некоторое изображение, при этом построенные точки, как правило, последовательно соединяют плавной линией.

Для выполнения этих заданий достаточно иметь обычную тетрадь в клеточку. За единичный отрезок принимается длина одной клеточки.

Задания:

1.“Машина” – работа Мещеряковой Софьи

(-1;7),(12;7),(13;0),(13;-1),(15;-1),(15;-3),(13;-3),(16;-3),(16;-5),(13;-5),(13;-3).

(14;-5),(13;-6),(11;-6),(11;-7),(10;-8),(8;-8),(7;-7),(7;-5),(8;-4),(10;-4),(11;-5),(11;-6).

(7;-6)(-6;-6)(-6;-5)(-7;-4)(-9;-4)(-10;-5)(-10;-7)(-9;-8)(-7;-8)(-6;-7).(-6;-6).

(-10;-6),(-12;-6),(-12;-5),(-14;-5),(-14;-3),(-11;0),(-6;3),(-3;3),(-1;7).

(13;-5),(11;-2),(8;-2),(6;-5),(-4;-5),(-6;-2),(-9;-2),(-12;-5).

(-3;3),(-4;1),(-2;1),(0;5),(-1;7).

(4;6),(9;6),(9;2),(4;2),(4;6).

2.“Лошадка” – работа Богомоловой Нины

(-7;3),(-7;7),(-6;8),(-6;9),(-5;8),(-4;9),(-4;8),(-2;3),(6;3),(7;4),(8;4),(10;1),(10;-2),(9;-2),(9;0),(7;1),(7;0),

(6;-4),(6;-8),(4;-8),(5;-7),(5;-4),(5;-2),(5;0),(5;-2),(4;-4),(5;-6),(4;-7),(3;-4),(4;-1),(3;0),(0;0),(-1;-4),(-1;-8)

(-3;-8),(-2;-7),(-2;0),(-2;-2),(-4;-4),(-3;-6),(-4;-7),(-5;-4),(-3;-1),(-4;1),(-5;5),(-6;3),(-7;3). (-6;6)

3.“Кораблик”- работа Захаренко Егора

(14;-7), (10;-11),(-10;-11),(-14;-7),(3;-7),(3;11),(0;10),(3;9),(-3;7),(-7;4);(-8;1),(-7;-3),(3;-7),(0;-1),

(0;0),(3;9).

4.“Котик” – работа Шаклановой Алены

(-8.5;0),(-11,5;3,5),(-11;5),(-10;8),(-8;10),(-6;11,5),(-5,5;10,5),(-4,5;11,5),(-4,5;10),(-3;8),(-2,5;6),(-3,5;5)

(-2;4),(0;4),(2,5;1,5),(4,5;-3),(5;-7),(17;-8,5),(16;-9),(3,5;-9),(2;-9,5),(-2,5;-10),(-4;-10),(-4,5;-9),(-3,5;-9),

(-2;-7,5),(-2;-6),(-3,5;-3),(-6;-8),(-6,5;-10),(-8;-10),(-9;-9,5),(-8;-8,5),(-8,5;-2,5),(-8,5;0). (-4;7,5)

5.“Верблюд” – работа Нейжмаковой Екатерины

(4;0),(6;0),(6;1),(5;2),(4;5),(3,5;7),(2,5;8),(1,5;9),(1,5;9),(1;6),(1;7),(1;9),(1;10),(0;9),(-1;9),(-1;10),

(-2;10),(-2;9),(-3;9),(-3;10),(-4;9),(-6;7),(-6;6),(-5;4),(-4,5;2),(-3;1),(-6;2),(-6,5;4),(-7;6),(-8;4),(-8,5;5),

(-10;6), (-10;8),(-10;10),(-9;11),(-10;11),(-12;11),(-13;10),(-15;9),(-16;8),(-16;7),(-15;6),(-14;7),(-12;7),

(-12;5),(-11;2),(-9;0),(-8;-1),(-8;-4),(-7;-5),(-7;-8),(-8;-10);(-4;-10),(-4;-8),(-4;-5),(-5;-4),(-5;-1),(-2;-4),

(-2,5;-5),(-2;-6),-2;-10),(0;-10),(-0,5;-8),(-1;-6),(-1;-4,5),(-1;-1),(1;-1),(2;-2),(3;-7),(2;-10),(5;-10),(5,-5),

(5;-1),(13;-1),(0;13),(-4;12),(-5;13),(8;11). (12;9,5)

6.“Белка” – работа Панфиловой Кристины

(-1,5;-0,5),(-1;0),-2;1),(-3;5),(-2;8),(-1;6),(1;6),(2;8),(3;5),(2;1),(1;0).

(0,5;0),(0,5;-1),(4;-5),(6;-1),(1,5;0,5),(5;-0,5),(7;5),(8;-4),(4;5),(2;-10),(-4;2),(-6;-3),(2;-10).

(3;-6),(7;-5),(5;-8),(7;-10),(2;-9),(3;-8).

(-5;0),(-6;6),(-6;0),(8;-1),6;-2)/

(-1;4),(-2;4),(-1,5;5),(-1;4).

(1;4),(2;4),(1,5;5),(1;4).

(-1;2),(1;1),(1;2).

7.“Зайка” – работа Антоновой Людмилы

(0;9),(1;9),(3;12),(4;14),(6;16),(10;19),(12;18),(11;15),(10,13),(3;6),(4;5),(5;3),(5;-1),(6,-1),(7;-2),(7;-5),

6;-6),(-6;-6),(-7;-5),(-7;-2),(-7,-2),(-6;-1),(-5;-1),(-5;3),(-4;5),(-3;6),(-5;8),(-7;6);(-11;5);(-12;6),(-10;8),

(-7;13),(-3;13),(-1;10),(-1;9),(0;9).

(1;3),(1;4),(1,5;5,5),(2,5;5,5),(3;4),(3;3),(1;3). (2;4).

(-1;3),(-1;4),(-1,5;5,5),(-2,5;5,5),(-3;4),(-3;3),(-1;3). (-2;4).

(-1;1),(1;1),(0;0),(-1;1).

(-2,5;-1,5),(-1;-2),(1;2),(2,5;-1,5),(0;-3),(-1;-2).

8.“Бабочка” -Пахтелева Никиты.

(6;0),(0,5;5,5), (0,5;4,5),(2;5),(3;6),(6;8),(9;9,5),(11,10),(13;9,5),(15;8,5),(14,5;7),(11;2),(9;0,5),(7;-1),

(6;-0,5),(5;-1),(4;-4),(3;-5),(2,5;-6,5),(1;-8),(0,5;-11),(0;-12),(-0,5;11),(-0,5;-9),(-1;-8,5),(-2;-8,5),

(-1,5;-7,5),(-3;-6),(-2,5;-4),(-2;-3),(-1,5;-2),(-1;-1),(-2;-2),(-3,5;-3,5),(-4;-2),(-5;-4),(-6;-5,5),(-7,5;-6),

(-8;-7),(-8,5;-6),(-9,5;-5,5),(-10,5;-5,5),(-12;-7),(-14;-8),(-12,5;-6),(-11,5;4),(-12;3),(-12;1),(-10;3),

(-11;3),(-11,5;5),(-14;7),(-14,5;11),(-15;13),(-14;14),(-13;14,5),(-10;14),(-9;13),-6;11),(-3;7),(-1,5;4,5).

(6;0),(-0,5;5,5),(-1,5;4,5),(-2;3),(-2;1),(-3;0),(-4,5;-1),(-4;-2).

(-1;-1),(-1;1),(0;2,5),(0,5;4,5).

(6,0),(1;7),(2,5;8,5),(3,5;9,5),(4,5;9).

(6;0),(-0,5;7),(-1;8,5),(-2;10),(-3,5;11,5).

Глоссарий

1. Числовая ось - прямая, на которой изображаются действительные числа

2. Абсцисса - лат. abscissa-отсекаемый (отрезок на оси иксов).

3. Ордината - лат. ordinatus – упорядоченный.

4. Координаты — величины, определяющие положение точки на плоскости .

5. Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

Полезные ссылки

Научить свободно ориентироваться на координатной плоскости, строить точки по заданным ее координатам и определять координаты точки, отмеченной на плоскости; четко и аккуратно выполнять построения, развивать творческие способности; воспитывать интерес к предмету http://rudocs.exdat.com/docs/index-350736.html

Координатная плоскость - это плоскость, на которой задана определенная система координат. Такая плоскость задается двумя прямыми, пересекающимися под прямым углом. В точке пересечения этих прямых находится начало координат. Каждая точка на координатной плоскости задается парой чисел, которые называют координатами.

Для того, чтобы нанести точки на координатную плоскость, Вы должны понимать организацию координатной плоскости и знать, что делать с координатами (х,у).

А также можете ознакомится в видеоуроках: 

• Координаты на плоскости https://www.youtube.com/watch?v=jR5LrA7O7QI
• Координаты на плоскости https://www.youtube.com/watch?v=aOhVGfdRtgU
• Координаты на плоскости https://www.youtube.com/watch?v=-6cmNCQ8xiM
• Координаты на плоскости https://www.youtube.com/watch?v=cb1xbqsROq8
• Координаты на плоскости https://www.youtube.com/watch?v=7r8lxyI_XUU

Библиография

• Координатная плоскость: что это такое? interneturok.ru
• Координатная плоскость https://yandex.ru/images?parent-reqid=1508953283350997-358084138840243251218244-sas1-5644&source=wiz
• Координатная плоскость http://www.yaklass.ru/
• Координатная плоскость http://letopisi.org/images
• Рисунки по координатам https://yandex.ru/images/search?text
• Стихи о математике, математических понятиях. http://www.elenaponomareva1987.ru/index/0-9
• Рене Декарт https://24smi.org/celebrity/5000-dekart.html
• Клавдий Птолемей https://ru.wikipedia.org/wiki/Клавдий_Птолемей
• Пьер Ферма https://ppt4web.ru/matematika/per-ferma.html
• Готфрид Вильгельм Лейбниц
• http://stud24.ru/geometry/istoriya-vozniknoveniya-koordinat-na-ploskosti/501431-1967470-page1.html
• http://nuclear-activity.narod.ru/simple8.html
• www.kvg.ee:82/KVG%20Online/...2017%20учебный%20год/Felert%20Larissa.pdf

В начало

Великие математики

АНАКСИМАНДР (Anaximandros) Милетский
около 610 – около 546 до н. э.

Анаксимандр (Anaximandros) Милетский – древнегреческий философ, представитель милетской школы. Считается учеником Фалеса Милетского и учителем Анаксимена. Не дошедшее до нас его сочинение «О природе» было первой философской работой, появившейся на греческом языке.
Анаксимандр впервые ввёл в философию понятие «архэ», лежащего в основе всех вещей первоначала, которым является апейрон – единая, вечная, неопределённая, т. е. бескачественная, материя, порождающая бесконечное многообразие сущего и выделяющая противоположности светлого и тёмного, тёплого и холодного. Апейрон предстаёт нам в виде трёх известных основных субстанций – воды, земли и огня, каковые субстанции находятся в вечной борьбе, однако некий естественный закон (необходимость) не позволяет одной стихии возобладать над другими.
Анаксимандр создал одну из первых геоцентрических моделей космоса и положил начало теории небесных сфер. В его космологии Земля представлялась неподвижным цилиндром, на верхней поверхности которого находится обитаемый мир (Ойкумена). Вселенная при этом мыслилась центрально-симметричной, поэтому у находящейся в центре Космоса Земли отсутствует основание двигаться в каком-либо направлении. Анаксимандр оказался, таким образом, первым мыслителем, кто предположил, что Земля свободно покоится в центре мира без опоры (в то время как его учитель Фалес Милетский считал, что Земля покоится на воде).
Анаксимандр учил о бесчисленности возникающих и гибнущих миров. Он составил первую географическую карту, изготовил первые в Греции солнечные часы и астрономические инструменты.

Гиппарх

Гиппарх, названный, по общему согласию ученых, великим астрономом древности, родился в Никеи, но время его рождения с точностью не известно, также нельзя сказать, когда он умер. Знаем только из Птолемея, что в 127 и 128 годах до нашей эры Гиппарх был в полном расцвете сил своей жизни.
В молодости Гиппарх наблюдал небо в своем родном городе, потом он поселился на остров Родос, тут им были произведены все важнейшие работы. Некоторые историки астрономии говорят, что он жил в А Александрии, но на это нет положительных доказательств, даже едва ли он бывал в этом городе.
Гиппарх написал весьма много сочинений, но до нас дошло только одно: «Комментарий на поэму Арата». Почти все погибли, и об их существовании знаем только из Птолемея и из других древних писателей.
Гиппарх сперва наблюдал прямые восхождения и склонения светила и превращал их в долготы и широты: это значит, что он положил основания сферической тригонометрии. Но т. к. тогда надо было производить долгие и тяжелые вычисления, он придумал снаряд (астролябию), посредством которого мог уже прямо определять долготы и широты. Сравнив эти долготы и широты с древнейшими выводами из наблюдений Аристилля и Тимохариса, он сделал открытие, обессмертившее его имя: он узнал, что точки равноденствие не постоянны на эклиптике, они отступают от востока к западу, т. е. расстояния звезд от эклиптики или их широты не меняются, меняются их склонения и их расстояния от экватора, а т. к. по предложению неподвижности земли в пространстве должен быть неподвижен и экватор, то отступление точек равноденствий или предварение равноденствий вынуждены были объяснять годичным обращением всей небесной сферы параллельно эклиптике и от запада к востоку.

Ферма Пьер (1601—1665)

Родился 17 августа 1601 г. в Бомон-де-Ломань, в семье городского советника, занимавшегося торговлей. Учился в Тулузе в местном университете. Получив юридическое образование, в 1631 г. Ферма поступает на государственную службу в кассационную палату Тулузского парламента (судебный орган). Первоначально он был уполномоченным по приёму прошений, а с 1648 г. повышен до звания советника.
Женился на дальней родственнице с материнской стороны — Луизе де-Лонг (1631 г.). Из пятерых детей, родившихся в семье, известен старший сын Самюэль, в 1679 г. издавший первое собрание сочинений своего отца.
Научные интересы Ферма касались множества областей. Изучив несколько языков, он увлекался поэзией, комментировал древних авторов, исследовал оптические явления. В течение всей жизни вёл обширную переписку со многими мыслителями, в том числе с Б. Паскалем, Р. Декартом.
Математика всегда оставалась для Ферма лишь хобби, и тем не менее он заложил основы многих её областей — аналитической геометрии, исчисления бесконечно малых, дифференциальных уравнений, теории вероятностей. Некоторые его открытия намного опередили своё время.
Известен как автор двух прославленных теорем по теории чисел, названных его именем: малой теоремы Ферма и великой теоремы Ферма. Относительно последней на полях одной из книг он писал: «Я нашёл этому поистине чудесное доказательство, но эти поля слишком малы для него».
По иронии судьбы именно великая теорема долгое время оставалась рекордсменом по числу неудачных попыток доказательства. Лишь в 1994 г. американский математик Э. Вайлз сумел сформулировать её общее доказательство.
Ферма также является автором открытия закона распространения света в различных средах.

Готфрида В. Лейбниц

Готфрид Вильгельм Лейбниц - немецкий философ, математик, логик, физик, изобретатель, богослов, историк, юрист, языковед, дипломат, чьи теоретические работы и практические изобретения в немалой степени повлияли на современную философию и науку. Основал Берлинскую Академию наук и был первым ее президентом.
Родился в Лейпциге в 1646 г., 11 июля. Его отцом был профессор университета, известный юрист, матерью - профессорская дочь, и во многом это предопределило будущую судьбу их сына. После отца, который умер, когда Готфриду было 6 лет, осталась огромная библиотека, в которой сын проводил дни напролет. Одаренность его была видна с детских лет. Мать определила его в лучшую в городе школу, а в 14 или 15 лет он уже был студентом Лейпцигского университета.
По уровню подготовки Лейбниц опережал многих старшекурсников. Ему не исполнилось 18-ти, когда он уже был магистром словесности и философии. В 1663 г. Готфрид Вильгельм проучился семестр в Йенском университете. В этом же году им была получена степень бакалавра, в следующем - степень магистра философии. В ноябре 1666 г. в Нюрнберге, Альторфском университете, Лейбниц успешно защищает докторскую диссертацию и отказывается от предложения остаться работать при этом учебном заведении.
В 1667 г. молодой ученый переезжает в Майнц, где знакомится с курфюстом, который высоко оценил уровень Лейбница и предложил ему поучаствовать в реформировании законодательства. На протяжении пяти лет при дворе ученый занимал видное положение; это был благоприятный период и в его творческой биографии: целый ряд политических и философских сочинений появился именно в эти годы.
С 1672 по 1676 г. Лейбниц живет в Париже, отправившись туда в составе дипломатической миссии. Пребывание во французской столице внесло огромный вклад в его развитие как ученого, в частности, математика. Так, в 1676 г. им были выработаны первые основания т.н. дифференциального исчисления, выдающегося математического метода. Именно точным наукам он в это время отдавал предпочтение.
В 1676 г. Лейбниц возвращается в Германию и поступает на службу к герцогам Ганновера, чтобы получать стабильный доход. Поначалу ему предоставили место библиотекаря, придворного советника, позже Лейбниц занимал должность историографа и тайного советника юстиции. В обязанности ученому вменялись самые разнообразные занятия, от написания исторических справок до опытов в алхимии. За 40 лет, проведенных в Ганновере, Лейбницем было написано огромное количество работ в области таких наук, как история, философия, математика, физика, право, языковедение, которые прославили его на всю Европу. Ученый инициировал создание Берлинского научного сообщества и в 1700 г. стал его первым президентом.

Игра

Чтобы закрепить навыки работы на координатной плоскости, было разработана игра «Алфавит на координатной плоскости». Каждый ученик получает карточку, где на координатной плоскости отмечены точками все буквы алфавита. Все карточки абсолютно одинаковы.

Игра позволяет отработать навыки:

— нахождения точки по ее координатам;

— нахождение координат точки.

Лайфхак

Ниже следующая история могла побудить Декарта к введению координат:

Физкультигра

Все встают из-за парт. На экране появляются координаты точек. Если точка принадлежит первой четверти, ребята должны потянуться. Если второй – наклониться вперед. Третьей – руки в стороны. Четвертой – сделать «восьмерку» сцепленными руками. Если точка находится на оси – хлопнуть в ладоши.