Математика: Натуралдык сандар менен болгон амалдар
Натуралдык сандар үчүн кийинки амалдар аныкталган: кошуу, кемитүү, көбөйтүү, бөлүү, даражага көтөрүү жана тамырдан чыгаруу. Эки амалдын негизинде гана натуралдык сандарды алышат. Ал кошуу жана көбөйтүү амалы.
Арифметикалык аракеттердин касиети
Кошуу, алуу көбөйтүү жана бөлүү аракеттери арифметикалык амалдар деп аталат. Алар кийинки касиеттерге ээ:
Содержание
Кошуунун касиеттери
1. Кошуунун орун которуу касиети: орун алмашуудан сумма өзгөрбоөйт.
a + b = b + a.
Бул барабардыкта a жана b каалаган натуралдык жана 0 мааниге ээ боло алат.
2. Кошуунун айкалыштыруу касиети: эки сандын суммасына үчүнчү санды кошуу биринчи санга экинчинин жана үчүнчү сандардын суммасын кошуу дегендик.
Тамга түрүндө:
(a + b) + c = a + (b + c)
Үч сандын суммасынын натыйжасы кашаалардын кандай койгонуна көз каранды эмес, керек болсо кашаалары жок эле кошсо да болот, айталы, a + b + с.
(a + b) + c = a + (b + c) = a + b + c
Кошуунун орун алмаштыруу же айкалыштыруу касиеттери суммасын кайра өзгөртүп түзүүгө мүмкүндүк бере алат.
3. Кошуудагы нөлдүн касиети
Эки натуралдык сандын суммасы дайыма ар бир кошулуучудан чоң болот. Бирок ал мындай болбойт, эгерде кошулуучунун бирөө нөл болсо.
Эгерде санга нөлдү кошсо ал сандын өзү келип чыгат.
a + 0 = 0 + a = a.
Кемитүүнүн касиеттери
1. Сандардын суммасынан кемитүүнүн касиети: Сандардын суммасынан кемитүү үчүн биринчи кошулуучуну кемитип, андан келип чыккан сандан экинчи кошулуучуну кемиткенге барабар.
a − (b + c) = (a − b) – c или a − (b + c) = (a − с) – b.
2. (a − b) − c туюнтмасындагы кашаалар эч кандай мааниге ээ эмес, аларды алып таштасак да болот.
(a − b) − c = a − b – c.
3. Сандардын суммасынан кемитүү касиети
Сандардын суммасынан кемитүү үчүн бир кошулуучудан кемитип, а натыйжасын калган кошулуучууга кошуу керек.
(a + b) − c = (a − c) + b (эгерде a > c же а = с)
или
(a + b) − c = (b − c) + a (эгерде b > c же b = с)
4. Кемитүүдөгү нөлдүн касиети:
Эгерде сандан нөлдү кемитсе ал сандын өзү келип чыгат.
a − О = a.
Эгерде сандан ошол санды кемитсе, анда нөл болот.
a − a = О.
Көбөйтүүнүн касиеттери
1. Көбөйтүүнүн орун алмаштыруу касиети
Орун алмашуудан көбөйтүндү өзгөрүлбөйт.
a • b = b • a
2. Көбөйтүүнүн айкалыштыруу касиети
Санды эки сандын көбөйтүндүсүнө көбөйтүү үчүн, алгач санды биринчисине, андан соң пайда болгон санды кийинки көбөйүүчүгө көбөйтсө болот.
a • (b • c) = (a • b) • c.
3. Көбөйтүүдө көлгө көбөйтүүнүн касиети Эгерде көбөйүүчүнүн бирөө эле нөлгө барабар болсо, анда ал көбөйтүндү нөлгө барабар болот.
a ∙ 0 = a,
0 • a • b • c = 0.
Көбөйтүндүнүн кошууга карата бөлүштүрүү касиети
Сумманы санга көбөйтүү үчүн, ал санды кошулуучулардын ар бирине көбөйтүп жана алынган натыйжаларды суммалап койсо болот.
(a + b) • c = a • c + b • c
Бул касиет каалагандай сандагы кошулуучулар үчүн туура болот.
(a + b + с + d) • k = a • k + b • k + c • k + d • k.
Көбөйтүндүнүн кемитүүгө карата бөлүштүрүү касиети
1. Айырманы санга көбөйтүү үчүн, алгач кемүүчүгө санды көбөйтүп, андан соң кемитүүчүгө көбөйтүп, биринчи пайда болгон сандан экинчи пайда болгон санды алып салса болот. Тамгалар түрүндө төмөндөгүчө болот:
(a − b) • c = a • c − b • c
2. Санды эки сандын көбөйтүндүсүнө көбөйтүү үчүн, алгач биринчи көбөйүүчүгө көбөйтүп, пайда болгон санды экинчи санга көбөйтсө болот.
Бөлүүнүн касиеттери
1. Бир дагы санды нөлгө бөлүүгө болбойт.
2. Нөлгө санды бөлүү нөлгө барабар.
О : a = О
3. Каалагандай санды 1ге бөлүү ал сандын өзүнө барабар.
b : 1 = b
4. Эгерде бөлүүнүүчүнү да бөлүүчүнү да бир эле натуралдык санга көбөйтсөк, анда андан пайда болгон тийинди өзгөрүүсүз калат.
a : b = (a • k) : (b • k), где k — любое натуральное число.
Бир нече амалдарга мисалдар
Мисалдар ар кандай амалдарды камтыйт. Бир нече амалдардан турган мисалдар менен иш алып барууда аныкталган эрежелер бар.
Эгерде мисал бир гана бөлүү менен алууну камтыса, амалдарды чыгаруу тартиби мааниге ээ эмес. Бирок эске алчу нерсе, “+” же ”-“ белгилерин белгилердин астында турган гана сандар үчүн колдоно алабыз.
Мисалы, 7 – 5 + 10. Бул 7 + 10 – 5 дегендей эле же – 5 + 7 + 10 десек да болот.
Эгерде дагы бир башка амалдар болсо анда чыгаруунун атайын бир аныкталган эрежесин пайдалат.
Маселедеги амалдарды чыгаруунун эрежеси
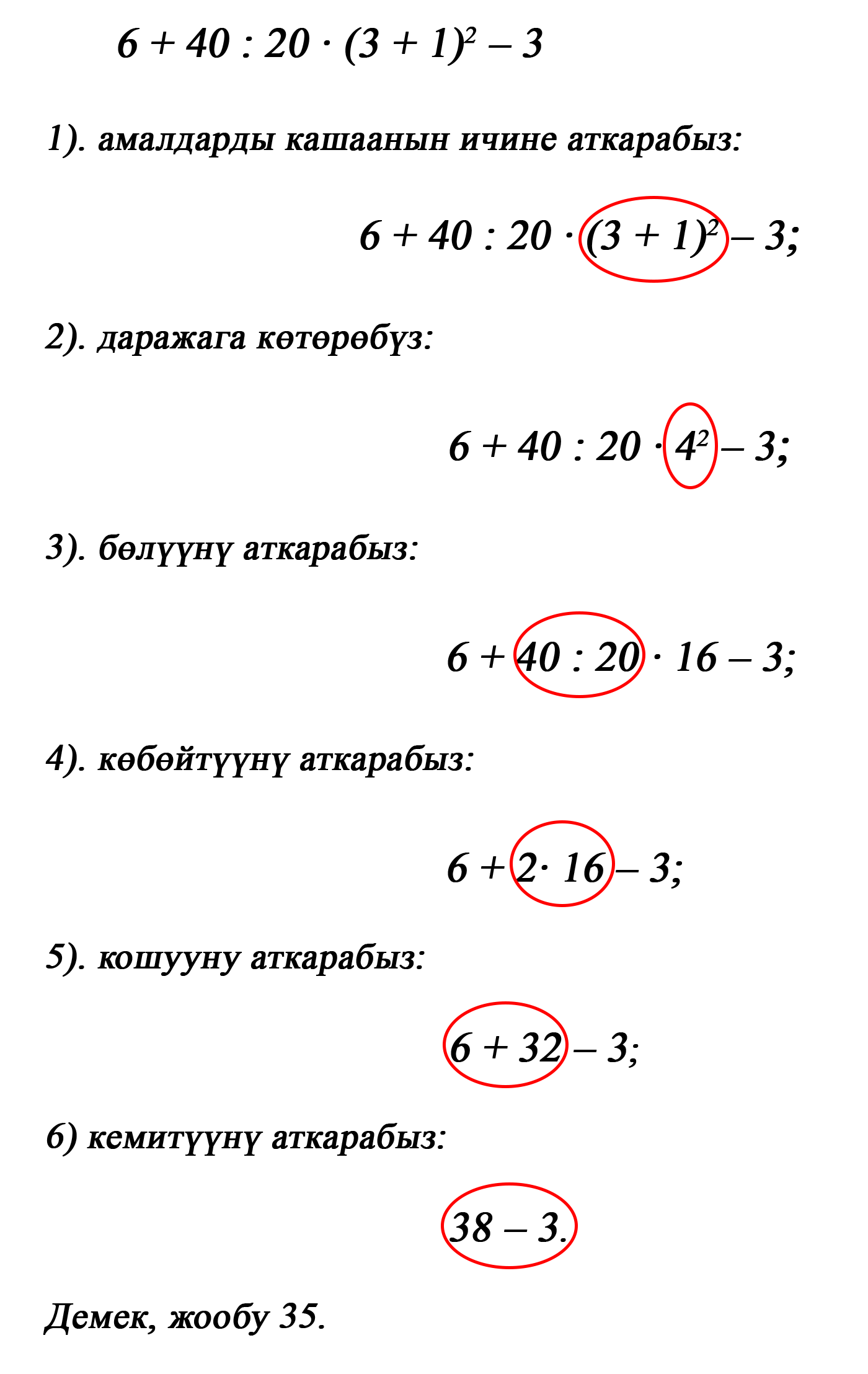
Маселеде, берилген ар кандай амалдарда алгач кашаанын ичиндеги амалдар чыгарылат, андан соң чоңунан кичинесине карай: даражасы-бөлуу-көбөйтүү-кошуу-алуу
Мисалы: маселенин маанисин табабыз.
Глоссарий
Амал – бул математикалык процесс, анда кээ бир эрежелер менен эки белгилүү сандан үчүнчү санды аныктап чыгышат.
Касиет — предметтин (объектинин) атрибуту.
а санынын n натуралдык сандагы даражасы 1ден чоң, деп, ар бири а га барабар болгон бирдей n сандардын көбөйтүндүсү. a∙a ∙ a∙…∙a=an
а санынын n даражасындагы тамыры деп, b саны аталат, мында bn=a, мында n>1.
Пайдалуу шилтемелер
Силер билесинерби, мурун математиканы билбегени үчүн ал адамды жумуштан кетиришкенин? Жок?! Анда көбөйтүүнүн жадыбалынын келип чыгышынын тарыхы тууралуу көрсөтүүнү көрүш керек го. Профессор Байыркы Египеттеги көбөйтүүнүн кызыктуу ыкмасын айтып берет, “манжа” менен тогузга көбөйтүүнүн ыкмасы менен тааныштырат. Андан тышкары геометрия менен аарынын соту курулушунун ортосундагы байланыш жүргүзүлгөн. Кызыктуу мисал көбөйтүүгө арналат. [Электрондук ресурс] //Академия Занимательных Наук YouTube, 2017. https://www.youtube.com/watch?v=vcKD1SURjfg . (кайрылуу датасы: 20.11.2017)
Библиография
- Штраус А.П. Тез эсептөөнүн ыкмалары [электрондук ресурс]//metod-kopilka.ru 2007-20017 URL:https:// www.metod-kopilka.ru/ priemi-bistrih-vichisleniy-61445.html. (кайрылуу датасы 20.11.2017)
- Кыргыздардын ченөө жана эсептөө системасы. : [Элетрондук ресурс]//Open/kg Ачык Кыргызстан. URL:https:// www.open/kg/about-kyrgyzstan/culture/ethnography/1970-sistemy-izmereniya-i-schet-u-kyrgyzov/html (кайрылуу датасы 20.11.2017)
- Акылыңда (көңүлүңдө) кантип бат эсептесе болот? Видеосу [Электрондук ресурс]//Жөнөкөй математика YouTube, 2017.https:// www.youtube.com/watch?v=hEVPZy4xaVQ (кайрылуу датасы 20.11.2017)
- Математика 51. Байыркы Египеддеги көбөйтүүнүн таблицасынын тарыхы- Кызыктуу илимдер Академиясы: [Электрондук ресурс]// Кызыктуу илимдер Академиясы YouTube, 2017 URL:https:// www.yuotube.com/watch?v=vcKDISURjfg. (кайрылуу датасы 20.11.2017).
- В.А.Гусев, А.Г.Мордкович Математика. Сурамжылоо материалдары М: Просвещение.1988.
- Математика: ОГЭге даярдык үчүн жаңы толук сурамжылоо. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. –Москва: АСТ 2017.-447бет(1)
- Окуучулар үчүн кроссворд. Математика. МантуленкоВ.Г., Гетменко О.Г.- Ярославль: “Өсүү академиясы”, 1998.-144бет.
ыргыздарда эсептөө жана ченөөнүн керектиги алардын коомдук өндүрүшүнүн жана социальдык дифференциалдык коомунун салыштырмалуу жогору өсүшүнүн шартында жаралган. Кыргыз элинде азыркыга чейин өзгөчө бир нече эсептөө системасы жашайт, ал ар кандай булактардан күбөлөндүрүлөт. Арифметиканын төрт амалы белгилүү: кошуу, алуу, көбөйтүү, бөлүү. Так санды алар алым-эсеп, жуп санды –туюк эсеп деп аташкан. Бул жөнөкөй математикалык билим алардын күнүмдүк турмушуна керек болгон. Ордо улуттук оюнунда (Хандын байгесине жетүү үчүн күрөш, кыргыздардын чоңдор үчүн эмоцианалдуу оюну), балдар оюнунда чүкө өкчөмөйдө математикалык кошуу, көбөйтүү амалдары оозеки бирдин учу-беш, бирдин учу – беш чүкө, бирдин учу бир-алты чүкө, бирдин учу эки-жети чүкө, экинин учу- он чүкө, экинин учу төрт- он төрт чүкө, бештин учу-жыйырма беш чүкө, кырктын учу-эки жүз чүкө болуп эсептелген.
Кыргыздардын илгерки “Тогуз кумалак” жана “Тогуз коргоол” оюндары (он майда жангактар же коргоолдор). Ал 18 казанбагы (ар биринде 9 дан коргоолу менен) бар жыгач тактадан жасалган. Ошондой эле утуп алган коргоолдор үчүн чоң казанбагы да бар.
Он сегиз энеси бар.
Бир жуз алтымыш эки баласы бар.
Имеет двух отцов,
Имеет восемнадцать матерей
И детей - сто шестьдесят два
Оюндун жүрүшү кийинкиче: эки оюнчу кезек менен коргоолдорду айлантып салып чыгат. Утуп алган коргоолдорун алар өздөрүнүн казанбагына чогултушат. Оюн ар бир оюнчудан чоң эркти жана өжөрлүктү талап кылат, башкысы акылдын ачбай чыңалышы керек. Оюндун жүрүшүндө өнөктөштөр акылы менен бири биринин кийинки жүрүшүн же өнөктөшүнүн кийинки оюн арифметикалык амалдардын баардык төрт түрүн тең бир эле маалда пайдалана эсептешкен.
Оюнчулардын эсеби жана тактикасы алардын ар биринин туура эмес жүрүш жасабоосу жана ошону менен бирге берки тарапка көп упай топтошуна мүмкүнчүлүк бериши болгон. Ойноп жаткан эки оюнчунун кимиси аналитикалык акылга жана куу акылман жүрүштөргө ээ болсо ошол гана жеңүүчү болгон.
Башка, татаалыраак оюн “Тогуз кумалак”. Байыркы кыргыздардын оюну “Чатыраш” делинген:
Анын баары болот отуз эки
Акылдуунун акылдуусу
Эл ичинде кыргыздардын бул өтө татаал оюнун өткөн кылымдарда индиялыктар үйрөнүшүп анан анын негизинде шахматты бүгүнкү түшүнүктө түзүп чыгышты деген версия бар. Ошондуктан бул интелектуалдык оюнга негизинен чоң кишилер жана өзгөчө хандар, бектер, аскер башчылар- эсепчилер катышышкан.
Мындай татаалдаштыруунун эмне кереги бар деп сиздер сурайсыздар. Баарыбыздын чөнтөк телефонубузда эсептегич (калькулятор) бар эмеспи. Ооба, көйгөй жок, бирок телефонуңуздун зарядкасы өчүп калган абалды элестетсеңиз сиз дүкөндөгү акылы жок адам көрүнгүңүз келбейби же кайырма акчаны туура алгыңыз келеби? Анда сизди кантип тез эсептөөгө үйрөнүүнүн айлаларын ачуучу видео сюжетти көрүүгө чакырабыз.
Кроссворд деген эмне? Сөздөр менен ойнолуучу интелектуалдык оюн Кроссворд деп аталат. Ал эске тутууну жакшыртат, ой жүгүртүү маданиятына жана жетпей жаткан маалыматты издөөгө үйрөтөт. Кроссвордду толтуруу мезгилинде сиз билген билимиңизди бекемдеп, ошондой эле сизде эстеп калуу сезимиңиз иштеп материалды эффективдүү эстеп калууга жардам берет.
Ошондо, сиз торчодогу тигинен баардык сөздөрдү жазуу мененсандар менен болгон арифметикалык амалдардын аталышын аласыз.
Кылымдар бою эл ичинде акылдуу макал лакаптар айтылып келген. Аларда кылымдан кылымга негизги турмуштук мааниси сакталып келатат. Сандардын макал лакаптарда колдонулушу адамдардагы байыркы убактан берки сандык эсептин өсүшүн сүрөттөйт. Макалдардагы эсептер өзгөчө мааниге ээ, анткени ар бир сан мурун кандайдыр бир башкача түшүнүктү берген.
Макалдарда ар түрдүү сандар кездешет, бирок көбүнчө 1 ден 9 га чейинки сандар көбүрөөк. Алардын мааниси ар кандай болушу жана талаш абалды мүнөздөшү мүмкүн. Буга мисал катары “согуш талаасындагы бирөө ал аскер эмес” дегенди алсак болот. Бул жерде ал кандай гана эр жүрөк кыйын болбосун, көйгөйдү башка бирөөнүн жардамы менен гана чече алаары айтылып жатат.
Силердин көңүлүңөрдү сандар менен эң кеңири тараган макал лакаптарга буралы.