Математика: Комбинаториканын негиздери
Версия от 16:37, 12 апреля 2018; Msu05 (обсуждение | вклад)
Илимдердин ханышасы – математикада, бүт баардык техниканы бир тармакка бириктирген илимди комбинаторика деп айтабыз. Комбинаторика — предметтердинкомбинацияларын жана орун алмашууларын окутуп-үйрөтө турган математиканын бир бөлүгү, латындан которгондо combinare – бириктирүү, айкалыштыруу дегенди түшүндүрөт. Эки жарым жүз жыл ичинде жаратылышты окуп-үйрөндүүдө математикалык талдоо негизги ролду ойногон.
Эки жарым жүз жыл аралыгында табиятты окуп-үйрөнүүдө математикалык талдоо негизги ролду ойноп келди. Абал тез ылдамдыкта эсептөөчү машина, компьютерлер пайда болгондон тартып түп тамыры менен өзгөрүлдү. Аларды жардамы менен мурун жүз жана миң жылдап талап калган тапшырмаларды чечип алуу оңойго турду. Дискреттик математиканын гүлдөөсү өзгөрүлүп жана байыркы дискреттик математиканын чөйрөсү – комбинаториканын да ролу өзгөрүлдү. Комбинаторика илим катары VIII кылымдарда пайда болгон, анткени ал учурда ыктымалдуулук теориясы кошо пайда болуп, маселени чыгарылыш ыктымалдуулугу үчүн элементтердин ар түрдүү комбинациясынын санын эсептөө керек болгон.
Сөөк менен ойноодогу ар түрдүү комбинациянын санын эсептөөгө алгачкылардан болуп италиялык математик Тарталья киришкен. Ал сөөктү канча ыкма менен жүргүзүүгө боло турган таблицаны түзгөн. Бирок ал ар түрдүү ыкма менен бир эле упай алынып калаарын эске алган эмес.Бара бара ар түрдүү оюндар пайда болгон (нарда, карта, шашка, шахмат ж.б.). Ар бир жолу фигуралардын түрдүү айкалыштарын карап, ким утуштуу комбинацияларды жана утулуштан кача билген оюнчу гана ута алганын кароого туура келген.
Белгилүү болгондой, покерде же оролмо оюндарда утуш ыктымалдуулугун эсептөөлөрүн жүргүзүү керек экендигинде, айталы, стрит-флешти 52 картанын ичинен чогултса болоорун. А эсептөөнү комбинаторикасыз жүргүзүү мүмкүн эмес.
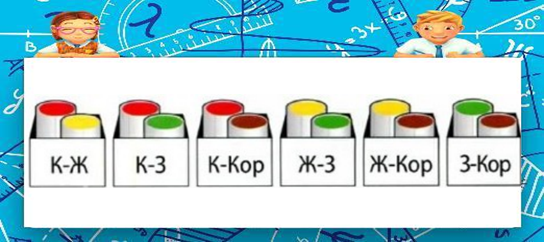
Эсептөөгө чейин тартипке салуу зарыл .Албетте, иш ордунун ирээтүүлүгүн айтабыз. Биз түшүнө турган комбинациянын санын объектисин тартипке салуу зарыл болот. Мейли, кызыл түстөгү төрт банкабыз бар: кызыл (К), сары (Ж), жашыл (3) ж/а күрөң (Кор), ар бирин экиден ар башка банкага аларды кутучаларга салыштыруу керек. Биз муну төмөндөгү мүнөздө жасасак болот:
Б.а. алты ар түдүү ыкма менен, бир кутучада сары жана кызыл түстөгү банкалар, ал тиги кызыл жана сары түстөгү банкалар менен бирдей болот. Бирок, түгөй түстөр менен биз желекчелерди боёшубуз керек, анда аны мындай кылуу керек: б.а. 12 ыкма менен; кызыл-сары желекче сары-кызыл менен бирдей болбойт.
Биздин жашообуз ар түрдүү программалардын көптүгүнөн турат. Тиги же бу тиешелүү программаны иштетиш үчүн туура келген сырсөздү киргизүү керек. Сырсөз катары программанын түрүнө карата сандар, сөздөр же сөздөрдүн айкалышын киргизүүгө туура келет. Комбинаторика музыкада, эмеректик ишмердүүлүктө, ар түрдүү оюндарда колдонулат (нарда, шахмат, шашка) ж.б. Кененирээк окугула: http://ya-znau.ru/znaniya/zn/80, а эгерде маселе чыгаргыңар келсе анда бул жакка өткүлө: http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html
1 мисал Тарелкада 5 алма жана 4 апельсин салынган. Канча ыкма менен бир жемишти тандоого болот. Чыгарылышы: Тапшырманын шарты боюнча алманы 5 ыкма, ал эми апельсинди 4 ыкма менен тандоого болот. Тапшырманын шарты болсо “же алма же пельсин” экендигин эске алуу менен 5+4=9 экенин табууга болот. Жообу: 9 ыкма.
2 мисал 1,4,7 сандарынан ар бири бир жолудан көп эмес колдонуп, канча эки маанилүү сан куроого болот? Чыгарылышы: 1 ыкма Варианттарды тандоо. Өткөрүп жибербес жана кайталабас үчүн бул сандарды өсүү тартибинде жазабыз. Алгач, 1 санына башталгандарды, андан сөн 4 жана 7 санына башталган сандарды жазабыз: 14, 17, 41, 47, 71, 74. Жообу: 6 сан.
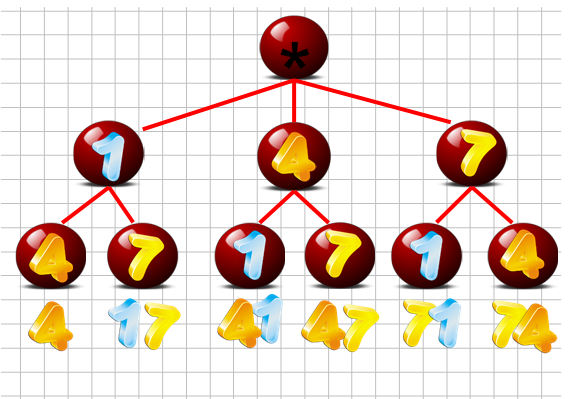
2 ыкма: Мүмкүн болгон вариантту дарак. Бул тапшырманы чыгаруу үчүн атайын схема курулган. Жылдызча коёбуз. Андан ары ал жылдызчадан 3 кесинди чыгарабыз. Тапшырманын шарты боюнча 3 сан берилген – 1,4,7, кесиндинин учтарына бул сандарды жазабыз. Андан соң, ар бир санга 2ден кесинди туташтырабыз. Алардан ары улап ар бир кесиндинин учуна 1, 4, 7 сандарын жазабыз. Жыйынтыгы: 14, 17, 41 47, 71, 74 болот. Б. А. баары 6 сан болот. Бул схема даракка окшош болгондуктан “дарак” деп аталат.
3 мисал
1,4,7 сандарынан ар бири бир жолудан көп эмес колдонуп, канча эки маанилүү сан куроого болот?
Чыгарылышы
Биринчи эки орунду санды үч ыкма менен тандоого болот. Биринчи санды тандагансоң, экинчи санды калган сандардан эки ыкма менен тандаса болот. Андан соң, изделүүчү үч маанилүү сандын жалпы саны 3*2 санын көбөйтүндүсүнө, бюаю 6га барабар болот. искомых трехзначных чисел равно произведению 3∙2, т.е. 6.
Жообу: 6 сан.
Которулуштуруу деп элементтери тартиби менен жайгашкан көптүк аталат. N элементтен турган мүмкүн болушунча которулуштуруу бул формула менен эсептелинет: Pn = n!
4 мисал. Финалдык чуркоодогу 8 катышуучу 8 чуркоочу тилкеге канча ыкма менен которулууга болот? Чыгаралышы. P8 = 8! = 40 320
Тапшырма
«Карышкыр, эчки жана капуста»
Дыйкан дарыянын аркы өйүзүнө карышкырды, эчкини жана капустаны алып өтүшү керек. Кайыкта орундук аз болгондуктан өзү менен кошо бирөөнү: карышкырды, эчкини же капустаны гана алып өтө алат. Бирок, карышкырды эчки менен калтырса карышкыр эчкини жеп салат, ал эми эчкини капуста менен калтырса капустаны эчки да жеп салат. Дыйкан эмне кылуу керек?
Маселени чыгаруу үчүн маселенин коюлуш шартына карата элементтерди өз ара жайгаштырууну колдонуу керек. Дыйкан бул жерде эчкини алып өтүү менен башташ керек болот. Андан соң жээке келип карышкырды тиги жээке алып келип кайра өзү менен кошо эчкини берки жээке ала кетиши керек болот. Ал жактан эчкини таштап капустаны тиги карышкыр турган жээкке алып келиш керек. Андан соң кайтып келип эчкини алып өтөт.
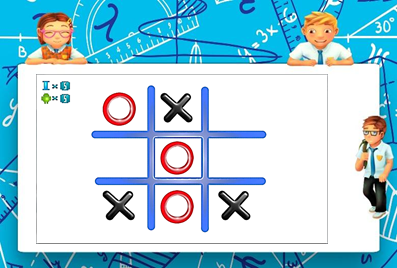
«Крестиктер-нөлдөр»
Эң белгилүү байыркы оюн. Квадратта 9 клеткага чийилген, оюнчулар кезеги менен бош клеткаларга крестик жана нөлдөрдү бир ктарга 3өө болгондой кылышып чийишет, толтурушат. Муну биринчи жасаган жеңишке ээ болот. Эгерде катасы жок толтурушса анда оюн тең-тең эсеби мене аяктайт. Каршылашың ката толтурган гана убакта утушка ээ болосуң. Эң туура жүрүш – бурчтагы клеткаларды ээлөө. Эгерде каршылашың сага жооп кылып ортоңку келтканы толтурса, анда анын утулганы.
«Ним»
Мейли бир же бир нече топтогу предеттер болсун. Оюнчулар топтордон төмөнкү эрежеге ылайык кезеги менен предметтерди алышат: канча сандагы предметти бир нече топтордон бир гана жолу алууга уруксаат берилет. Көпчүлүккө белгилүү болгон жана жеңишке алып барган оюндун бир нече варианты бар.
Глоссарий
Комбинаторика - предметтердин орун алмашышын жана комбинациясын окуп-үйрөтө турган математиканын бир бутагы.
Библиография
- Комбинаторика. https://infourok.ru/kombinatorikaeto-interesnonauchniy-proekt-sekciya-matematika-816469.html
- Комбинаторика: основные правила и формулы. http://ya-znau.ru/znaniya/zn/80
- Савельев Л.Я. Комбинаторика и вероятность. – Новосибирск, Наука, 1975.
- Тюрин Ю.Н., Макаров А.А., Высоцкий И.Р., Ященко И.В. Теория вероятностей и статистика. – М.: МЦНМО: АО «Московские учебники», 2004.
1. Мындан 35 кылым мурун египеттик фараон Тутанхамондун сөөгү коюлган пирамидада предметтердин арасынан байыркы“сенет” оюну үчүн үч горизоталдуу тактаны табышкан. Кийинчерээк нарданы, шашканы жана шахматты.
2. Алгачкы комбинаторикага жакын делинген кездешүүлөрдү кытайдын “Өзгөрмө китеби” колжазмаларынан жолуктурууга болот.
3. Комбинаториканын өнүгүшүнө өзгөчө секирикти кумар оюнчары болгон сөөк оюндары түрткү берген.
4. Комбинаториканын ыкмасы менен тексттин үстүнөн комбинациялардын кайталаныш окшоштугун байкоодо эсептөөгө болгон.
5. Рубик кубиги – бул 27 бирдей кубка бөлүнгөн куб. Алгачкы абалында кубдун ар бир кырлары 6 түстүн бири менен боёлгон. Курч акылдуу механизм анын борбору менен кесилишкен каалагандай 9 кубиктин катмарын которууга мүмкүндүк берет. Мында чектеринин түстөрү аралашат. Маселе түрдүү түстөгү кубиктин кырларын алгачкы абалга алып келүүдө жатат. Теориялык жактан кубиктин каалагандай абалынан алгачкы абалына 23 жүрүштөн ашык эмес жүрүш менен келүүгө болот.
Мурун 1982-жылы дүйнөлүк чемпионатта Рубик кубигин чогултуунун ылдамдыгын 22,95 секунд деп көрсөткөн. А биздин учурда болсо балдарыбыз аз эле секунддада чогултат. Келгиле ынанып көрөлү
Жооптор:
- Вариант
- Сочетания
- Факториал
- Событие
- Исход