Физика: Физика и методы ее изучения — различия между версиями
Msu05 (обсуждение | вклад) |
Msu05 (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | <div class= | + | __NOTOC__ |
| − | + | <div class="row mat-bg> | |
| + | <div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> | ||
| + | {{Якорь|Начало}} | ||
| − | + | ==Основная информация== | |
| − | + | Примерно в то же время, когда жители древних цивилизаций научились вычислять площади различных фигур, появилась необходимость и в вычислении объемов. Эта задача в первую очередь была связана с развитием торговли и строительства. С развитием математики появилась отдельное направление – [https://ru.wikipedia.org/wiki/%D0%A1%D1%82%D0%B5%D1%80%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F стереометрия] (раздел геометрии, который занимается изучением пространственных фигур), упоминания о котором встречались уже в IV веке до нашей эры. | |
| − | + | Египтяне использовали эту науку в различных хозяйственных работах, при сооружении оросительных каналов, грандиозных храмов и пирамид, при высечении из гранита знаменитых сфинксов. | |
| − | + | Содержащиеся в дошедших до нас папирусах геометрические сведения и задачи почти все относятся к вычислению площадей и объемов. В них нет никаких указаний на способы вывода тех правил, которыми пользовались египтяне для вычисления длин, площадей и объёмов; часто употреблялись правила приближённых подсчётов. Высшим достижением египетской геометрии следует считать точное вычисление объёма усечённой пирамиды с квадратным основанием, содержащееся в «[https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D1%81%D0%BA%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D0%B9_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BF%D0%B0%D0%BF%D0%B8%D1%80%D1%83%D1%81 Московском папирусе]». | |
| − | + | Поиск формул, позволяющих вычислять объемы различных тел, был долгим. В древнеегипетских папирусах, в вавилонских клинописных табличках встречаются правила для нахождения объема усеченной пирамиды. Определять объемы призмы, пирамиды, цилиндра и конуса умели древние греки еще задолго до [https://ru.wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D0%BC%D0%B5%D0%B4 Архимеда]. Но только он знал общий метод, позволяющий определить любую площадь или объем. Идеи Архимеда легли в основу интегрального исчисления. Сам ученый определил с помощью своего метода площади и объемы почти всех тел, которые рассматривались в античной математике. На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда - о том, что объемы этих тел относятся как 3:2. В памятниках вавилонской и древнеегипетской архитектуры встречаются такие геометрические фигуры, как куб, параллелепипед, призма. Важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных фигур. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения. Объемы зерновых амбаров и других сооружений в виде кубов, призм и цилиндров египтяне и вавилоняне, китайцы индийцы вычисляли путем умножения площади основания на высоту. Однако древнему Востоку были известны только отдельные правила, найденные опытным путем. В более позднее время был найден общий подход к вычислению объемов многогранников. | |
| + | <div class="show-for-large-up">{{center|[[Файл:Архимед биография легенды.jpg|650px]]}}</div> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:Архимед биография легенды.jpg|650px]]}}</div> | ||
| − | + | Все тела, которые нас окружают, имеют объём. В повседневной жизни мы часто сталкиваемся с телами разных форм и объемов. Например, мы говорим, что ведро вмещает в себя 10 литров воды. Это означает, что объем ведра - 10 литров. Другой пример: на строительство садового домика понадобилось 20 кубометров (или кубических метров) древесины. Как видно, в этих примерах объемы выражаются определенными числами, но в разных единицах - в одном случае в литрах, в другом - в кубических метрах. В разных единицах объем одного и того же тела выражается разными числами. | |
| − | + | В древности у разных народов были свои меры измерения. Так в Киевской Руси существовала мера зерна – кадь, равная 230 кг ржи. Жидкости мерили бочками и вёдрами. В XIX веке система мер имела вид: 1 бочка = 40 ведрам, ведро = 10 штофам, 1 штоф = 2 бутылям, бутыль = 10 чаркам. | |
| − | + | В нашей стране существовали свои единицы измерения. Для нахожденияы объемов сыпучих тел употребляли предметы домашнего обихода. Объемы сыпучих и жидких тел обозначались следующим образом: кыпындай — с крошку, таруудай — с зернышко проса, тырмактын агындай — с белую часть ногтя, бир чьшчым — щепотку, бир ууч — горсть, бир кочуш — пригоршню, бир кашык — с ложку, бир аяк — с чашку средней величины. У дехкан практиковалась такая единица измерения объема и веса, как байс. Она равнялась весу 100 зерен ячменя, а 100 байсов составляли 3 килограмма зерна. Когда дехкане получали, давали взаймы или продавали зерно, то считали так: 200 байсов, составлявшие 6 килограммов ячменя, принимали за единицу, называвшуюся чакса; более крупной мерой веса были 2 чаксы — бир нимшек, или 12 килограммов, бир шимек —4 чакса, или 48 килограммов. Часто зерно измеряли более простым способом: брали 100 или 200 байсов зерна, засыпали в какой-нибудь сосуд и измеряли количество зерна по высоте от дна сосуда по суставам пальцев рук. В этом случае процесс измерения проходил намного быстрее, но неточность увеличивалась. | |
| − | |||
| − | |||
| − | |||
| − | + | Количество зерна измерялось также кап — мешками, которые имели разную вместимость. Самый большой кап имел высоту в рост жеребенка и назывался тай кап; его вместимость была равна одному батману пшеницы или 12 пудам. В народных эпосах упоминаются богатыри, которые за один присест могли съесть не один батман зерна: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | + | <div class="blocktext"><center>'''Семь батманов пшеницы за раз съел'''<br> |
| − | |||
| − | '' | ||
| − | |||
| − | < | + | '''Хлебом пахнущий огромный Джолой.'''</center></div> |
| − | < | + | |
| − | < | + | Так что же такое объём? |
| − | + | ||
| + | '''Объём — количественная характеристика пространства, занимаемого телом или веществом'''. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. | ||
| + | |||
| + | В формулах для обозначения объёма используется заглавная латинская буква '''V''', являющаяся сокращением от латинского '''volume''' — «объём», «наполнение». | ||
| + | |||
| + | За единицу измерения объема принимается куб, ребро которого равно единице измерения отрезков. Это кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр или даже кубический километр. Часто для измерения объёма жидкости используют единицу измерения 1литр. Схема перевода одной единицы измерения объема в другую приведена ниже. | ||
| + | |||
| + | <div class="show-for-large-up">{{center|[[Файл:Соотношения между единицами объема.gif|650px]]}}</div> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:Соотношения между единицами объема.gif|650px]]}}</div> | ||
| + | |||
| + | Объёмы обладают следующими свойствами: | ||
| + | |||
| + | 1. Объем тела есть неотрицательное число. | ||
| + | |||
| + | 2. Равные тела имеют равные объемы | ||
| + | |||
| + | 3. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел. | ||
| + | |||
| + | Согласно третьему свойству, чтобы найти объём прямоугольного параллелепипеда, нужно разбить его на кубы с ребром, равным единице измерения. Но такой способ измерения объёмов неудобен, поэтому применяют формулу для вычисления объёма прямоугольного параллелепипеда V=abc. Формулы для вычисления других геометрических тел немного сложнее. Несмотря на это их надо знать уметь применять при решении математических задач и в жизни. В своей практической деятельности человек часто встречается с необходимостью вычисления объёмов, например, при изготовлении каких-либо деталей или при строительстве различных сооружений. Многие строительные объекты, детали конструкций и другие предметы имеют форму геометрических тел: параллелепипедов, призм, цилиндров, шаров. | ||
| + | Предлагаем таблицу, в которые вошли часто используемые геометрические тела и формулы нахождения их объема. Распечатайте и используйте! | ||
| + | <div class="show-for-large-up">{{center|[[Файл:Геометрич_тела.gif|650px]]}}</div> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:Геометрич_тела.gif|650px]]}}</div> | ||
| − | |||
| − | < | + | <div class="show-for-large-up">{{center|[[Файл:2_таблицы_объем.jpg|650px]]}}</div> |
| − | + | <div class="hide-for-large-up">{{center|[[Файл:2_таблицы_объем.jpg|650px]]}}</div> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |} | ||
| − | </ | ||
| − | |||
| + | ==Полезные ссылки== | ||
| − | + | Проект "Самообразование" служит для представления знаний в понятной, ясной и краткой форме, удобной для восприятия человеком, не имеющим специальной подготовки в той или иной научной области. Здесь представлены задачи из открытого банка задач по ЕГЭ математика профильный уровень за предыдущие годы. Все задачи разбиты по темам и содержат подробное решение. Это поможет быстро сориентироваться в каталоге и выбрать для себя те темы, которые его интересуют. Вперед, к знаниям! http://self-edu.ru/math_egecats.php | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Здесь вы найдете много полезных и нужных формул, таблиц и справочной информации. А онлайн калькулятор поможет рассчитать объем. Для расчета задайте необходимые данные. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров. Попробуем? http://mozgan.ru/Geometry#block1 | |
| + | ==Глоссарий== | ||
| + | ''Геометрическое тело'' - это «то, что имеет длину, ширину и глубину» в «Началах» Евклида, а в учебниках элементарной геометрии - «часть пространства, ограниченная своей образуемой формой». | ||
| − | ''' | + | ''Многогранник'' – геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости. Содержит углы, вершины, грани и ребра. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '' | + | ''Конус'' - это тело, которое состоит из круга – основание конуса, точки, не принадлежащей плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса и точки окружности основания. Получается в результате вращения прямоугольного треугольника вокруг одного из катетов. |
| − | + | ''Куб'' – это прямоугольный параллелепипед с равными ребрами. | |
| − | ''' | + | ''Параллелепипед'' – это четырехугольная призма, основаниями которой являются параллелограммы. |
| − | ''' | + | ''Пирамида'' - это многогранник, который состоит из многоугольника — основания пирамиды, и треугольников, имеющих общую вершину, называемых боковыми гранями пирамиды. |
| − | ''' | + | ''Призма'' - это многогранник, поверхность которого состоит из двух равных многоугольников и параллелограммов, имеющих общие стороны с каждым из оснований. |
| − | '' | + | ''Тела вращения'' – это геометрические тела, полученные в результате вращения некоторой фигуры (обычно плоской) вокруг прямой. |
| − | '' | + | ''Цилиндр'' — тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра. Получается в результате вращения прямоугольника вокруг одной из его сторон. |
| − | '' | + | ''Шар'' - это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Получается в результате вращения полукруга вокруг его диаметра. |
| − | + | == Библиография == | |
| + | *Архимед [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88903749, сохранённая в 10:33 UTC 10 ноября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL:https://ru.wikipedia.org/wiki/Архимед (дата обращения: 20.11.2017) | ||
| + | *ЕГЭ математика. Профильный уровень. Каталог заданий по темам. : [Электронный ресурс] // Самообразование. URL: http://self-edu.ru/math_egecats.php (дата обращения: 20.11.2017) | ||
| + | *Мозган Онлайн калькулятор. : [Электронный ресурс] // mozgan.ru. URL: http://mozgan.ru/Geometry#block1 (дата обращения: 20.11.2017) | ||
| + | *Системы измерения и счет у кыргызов.: [Электронный ресурс] //Open.kg Открытый Кыргызстан. URL: https://www.open.kg/about-kyrgyzstan/culture/ethnography/1970-sistemy-izmereniya-i-schet-u-kyrgyzov.html . (дата обращения: 20.11.2017) | ||
| + | *Как посчитать объем - формулы расчета. : [Электронный ресурс] // «ФБ», 2017. URL: http://fb.ru/article/143418/kak-poschitat-obyem---formulyi-rascheta (дата обращения: 20.11.2017) | ||
| + | *Загадки в стихах о геометрических фигурах и телах. : [Электронный ресурс] //Литературный проект "Ковдория" 2007 - 2012 URL: http://igri-uma.ru/forum/index.php?showtopic=3936 (дата обращения: 20.11.2017) | ||
| + | *Пирамида (геометрия) [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 85954734, сохранённая в 15:42 UTC 13 июня 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Пирамида_(геометрия) (дата обращения: 20.11.2017) | ||
| + | *Призма (геометрия) [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 87437416, сохранённая в 14:58 UTC 4 сентября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Призма_(геометрия) (дата обращения: 20.11.2017) | ||
| + | *Куб [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88557583, сохранённая в 15:36 UTC 25 октября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Куб (дата обращения: 20.11.2017) | ||
| + | *Прямоугольный параллелепипед [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 87981530, сохранённая в 19:25 UTC 30 сентября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Прямоугольный_параллелепипед (дата обращения: 20.11.2017) | ||
| + | *Цилиндр [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 85933764, сохранённая в 15:46 UTC 12 июня 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL:http://ru.wikipedia.org/?oldid=85933764 (дата обращения: 20.11.2017) | ||
| + | *Конус [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 87095971, сохранённая в 10:39 UTC 16 августа 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL:https://ru.wikipedia.org/wiki/Конус. URL:(дата обращения: 20.11.2017) | ||
| − | |||
| − | + | </div> | |
| − | + | <!-- Sidebar --> | |
| + | <div class="large-4 medium-5 columns"> | ||
| + | <!-- Первый элемент сайдбара Это интересно или топ5/10/15 --> | ||
| + | <div class="shadow radius sbstyle"> | ||
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Это Интересно</div> | ||
| + | </div> | ||
| + | <span class="firstcharacter">Р</span><p align="justify">азличные прикладные задачи на определение объема. <br> | ||
| − | + | <div class="show-for-large-up">{{center|[[Файл:Различные прикладные задачи на определение объема.jpg|400px]]}}</div> | |
| + | <div class="hide-for-large-up">{{center|[[Файл:Различные прикладные задачи на определение объема.jpg|400px]]}}</div> | ||
| − | |||
| − | + | Вернемся к проблеме: как посчитать объем перевозимых грузов. Каким является груз: фасованным или сыпучим? Каковы параметры тары? Вопросов больше, чем ответов. Немаловажным станет вопрос массы груза, поскольку транспорт отличается грузоподъемностью, а трассы – максимальным весом транспортного средства. Нарушение правил перевозки грозит штрафными санкциями. | |
| − | <div class= | + | <div class="blocktext">Задача 1. Пусть груз представляет собой прямоугольные контейнеры, заполненные товаром. Зная вес товара и контейнера, можно с легкостью определить суммарный вес. Объем контейнера определяем, как объем прямоугольного параллелепипеда. Зная грузоподъемность транспорта, его габариты, можно просчитать возможный объем перевозимого груза. Верное соотношение этих параметров позволяет избежать катастрофы, преждевременного выхода транспорта из строя. </div> |
| − | + | Вопрос определения объемов играет немаловажную роль в строительстве. Возведение домов, других сооружений – дело затратное, стройматериалы требуют внимательного отношения и предельно точного расчета. Основа здания – фундамент - представляет собой обычно литую конструкцию, заполняемую бетоном. Перед тем как посчитать объем бетона, необходимо определить тип фундамента. Плитный фундамент – плита в виде прямоугольного параллелепипеда. Столбчатое основание - прямоугольные или цилиндрические столбы определенного сечения. Определив объем одного столба и умножив его на количество, можно рассчитать кубатуру бетона на весь фундамент. Рассчитывая объем бетона для стен или перекрытий, поступают достаточно просто: определяют объем всей стены, умножая длину на ширину и высоту, затем отдельно определяют объемы оконных и дверных проемов. Разность объема стены и суммарного объема проемов – объем бетона. | |
| − | + | Некоторые прикладные задачи требуют знаний об объеме зданий и сооружений. К ним относятся проблемы ремонта, реконструкции, определения влажности воздуха, вопросы, связанные с теплоснабжением и вентиляцией. Прежде чем ответить на вопрос о том, как посчитать объем здания, делают замеры по внешней его стороне: площади сечения (длина умножается на ширину), высоты здания от нижней части первого этажа до чердака. Определение внутренних объемов отапливаемых помещений проводят по внутренним обводкам. | |
| − | + | Современные квартиры и офисы невозможно представить без системы отопления. Основной частью систем являются батареи и соединительные трубы. Как посчитать объем системы отопления? Полный объем всех секций отопления, который указан на самом радиаторе, необходимо сложить с объемом труб. И на этом этапе встает проблема: как посчитать объем трубы. Представим, что труба – цилиндр, решение приходит само собой: используем формулу расчета объема цилиндра. В отопительных системах трубы заполняются водой, поэтому необходимо знать площадь внутреннего сечения трубы. Для этого определяем ее внутренний радиус. Формула определения площади круга известна из курса геометрии. Общая длина труб определяется по их протяженности в помещении. </p> | |
| + | </div> | ||
| + | <!-- Второй элемент сайдбара --> | ||
| + | <div class="shadow radius sbstyle" style="margin-top:20px;"> | ||
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Загадки</div> | ||
| + | </div> | ||
| + | |||
| + | <div class="blocktext"> | ||
| + | Вопрос: «Почему сложные загадки опасны для людей?»<br> | ||
| + | Ответ: «Потому, что люди над ними ломают свои головы.»</div> | ||
| + | |||
| + | Разгадывать загадки – очень увлекательное занятие. Ведь они учат думать и анализировать, расширяют знания о мире, пополняют словарный запас. Загадки прекрасно развивают мышление, логику, память. И делают это непринужденно, в игровой форме. Ведь искать разгадку так весело и интересно! Ну, а поскольку в таком состоянии думать тяжело, сразу приводим ответ, надо лишь немного подождать, чтобы его увидеть. | ||
| + | |||
| + | <div class="show-for-large-up">{{center|[[Файл:1_.gif|500px]]}}</div><br> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:1_.gif|500px]]}}</div><br> | ||
| − | |||
| − | |||
| − | |||
| − | + | <div class="show-for-large-up">{{center|[[Файл:2_1.gif|500px]]}}</div><br> | |
| − | + | <div class="hide-for-large-up">{{center|[[Файл:2_1.gif|500px]]}}</div><br> | |
| + | |||
| + | |||
| + | <div class="show-for-large-up">{{center|[[Файл:3_2.gif|500px]]}}</div><br> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:3_2.gif|500px]]}}</div><br> | ||
| + | |||
| − | + | <div class="show-for-large-up">{{center|[[Файл:4_3.gif|500px]]}}</div><br> | |
| − | + | <div class="hide-for-large-up">{{center|[[Файл:4_3.gif|500px]]}}</div><br> | |
| − | + | ||
| − | + | ||
| − | + | <div class="show-for-large-up">{{center|[[Файл:5_4.gif|500px]]}}</div><br> | |
| − | + | <div class="hide-for-large-up">{{center|[[Файл:5_4.gif|500px]]}}</div><br> | |
| − | + | ||
| − | + | <div class="show-for-large-up">{{center|[[Файл:6_5.gif|500px]]}}</div><br> | |
| + | <div class="hide-for-large-up">{{center|[[Файл:6_5.gif|500px]]}}</div><br> | ||
| + | |||
| + | <div class="show-for-large-up">{{center|[[Файл:7_6.gif|500px]]}}</div><br> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:7_6.gif|500px]]}}</div><br> | ||
| + | |||
| + | <div class="show-for-large-up">{{center|[[Файл:8_7.gif|500px]]}}</div><br> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:8_7.gif|500px]]}}</div><br> | ||
| + | |||
| + | <div class="show-for-large-up">{{center|[[Файл:9_8_.gif|500px]]}}</div> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:9_8_.gif|500px]]}}</div> | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <!-- третий элемент сайдбара викторины игры тесты --> | ||
| + | <div class="shadow radius sbstyle" style="margin-top:20px;"> | ||
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Лайфхак</div> | ||
| + | </div> | ||
| + | |||
| + | Многие из вас скажут, как же применять на практике геометрические формулы, если запомнить их очень сложно, а для некоторых это просто набор букв и цифр. В этом поможет мнемотехника: каждой или нескольким единицам информации «присваивается» образ, и далее связываются данные образы. Чтобы вспомнить (воспроизвести) данную информацию, порядок действия будет обратный: вспоминаются связанные между собой образы, а затем – то, что под ними подразумевалось. Таким образом, фактически сначала мы кодируем, зашифровываем данные в форму, удобную для запоминания, а когда они нам понадобятся, мы достаем их из памяти и расшифровываем. Звучит сложно? Тогда смотрим видео ролик «Как запомнить формулы объема» | ||
| + | |||
| + | |||
| + | <div class="show-for-large-up">{{center|[[Файл:Как_запомнить_формулы_объема.mp4|450px]]}}</div> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:Как_запомнить_формулы_объема.mp4|450px]]}}</div> | ||
| − | + | </div> | |
| − | |||
| − | |||
| + | ==Игра== | ||
| + | {{#widget:Iframe | ||
| + | |url=https://learningapps.org/view3979682 | ||
| + | |width=90% | ||
| + | |height=410 | ||
| + | |border=0 | ||
| + | }} | ||
</div> | </div> | ||
| − | + | <div class="light" style="float:right;>[[#Начало|В начало]]</div> | |
| − | |||
| − | |||
| − | |||
| − | |||
Версия 12:20, 27 ноября 2017
Основная информация
Примерно в то же время, когда жители древних цивилизаций научились вычислять площади различных фигур, появилась необходимость и в вычислении объемов. Эта задача в первую очередь была связана с развитием торговли и строительства. С развитием математики появилась отдельное направление – стереометрия (раздел геометрии, который занимается изучением пространственных фигур), упоминания о котором встречались уже в IV веке до нашей эры.
Египтяне использовали эту науку в различных хозяйственных работах, при сооружении оросительных каналов, грандиозных храмов и пирамид, при высечении из гранита знаменитых сфинксов.
Содержащиеся в дошедших до нас папирусах геометрические сведения и задачи почти все относятся к вычислению площадей и объемов. В них нет никаких указаний на способы вывода тех правил, которыми пользовались египтяне для вычисления длин, площадей и объёмов; часто употреблялись правила приближённых подсчётов. Высшим достижением египетской геометрии следует считать точное вычисление объёма усечённой пирамиды с квадратным основанием, содержащееся в «Московском папирусе».
Поиск формул, позволяющих вычислять объемы различных тел, был долгим. В древнеегипетских папирусах, в вавилонских клинописных табличках встречаются правила для нахождения объема усеченной пирамиды. Определять объемы призмы, пирамиды, цилиндра и конуса умели древние греки еще задолго до Архимеда. Но только он знал общий метод, позволяющий определить любую площадь или объем. Идеи Архимеда легли в основу интегрального исчисления. Сам ученый определил с помощью своего метода площади и объемы почти всех тел, которые рассматривались в античной математике. На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда - о том, что объемы этих тел относятся как 3:2. В памятниках вавилонской и древнеегипетской архитектуры встречаются такие геометрические фигуры, как куб, параллелепипед, призма. Важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных фигур. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения. Объемы зерновых амбаров и других сооружений в виде кубов, призм и цилиндров египтяне и вавилоняне, китайцы индийцы вычисляли путем умножения площади основания на высоту. Однако древнему Востоку были известны только отдельные правила, найденные опытным путем. В более позднее время был найден общий подход к вычислению объемов многогранников.
Все тела, которые нас окружают, имеют объём. В повседневной жизни мы часто сталкиваемся с телами разных форм и объемов. Например, мы говорим, что ведро вмещает в себя 10 литров воды. Это означает, что объем ведра - 10 литров. Другой пример: на строительство садового домика понадобилось 20 кубометров (или кубических метров) древесины. Как видно, в этих примерах объемы выражаются определенными числами, но в разных единицах - в одном случае в литрах, в другом - в кубических метрах. В разных единицах объем одного и того же тела выражается разными числами.
В древности у разных народов были свои меры измерения. Так в Киевской Руси существовала мера зерна – кадь, равная 230 кг ржи. Жидкости мерили бочками и вёдрами. В XIX веке система мер имела вид: 1 бочка = 40 ведрам, ведро = 10 штофам, 1 штоф = 2 бутылям, бутыль = 10 чаркам.
В нашей стране существовали свои единицы измерения. Для нахожденияы объемов сыпучих тел употребляли предметы домашнего обихода. Объемы сыпучих и жидких тел обозначались следующим образом: кыпындай — с крошку, таруудай — с зернышко проса, тырмактын агындай — с белую часть ногтя, бир чьшчым — щепотку, бир ууч — горсть, бир кочуш — пригоршню, бир кашык — с ложку, бир аяк — с чашку средней величины. У дехкан практиковалась такая единица измерения объема и веса, как байс. Она равнялась весу 100 зерен ячменя, а 100 байсов составляли 3 килограмма зерна. Когда дехкане получали, давали взаймы или продавали зерно, то считали так: 200 байсов, составлявшие 6 килограммов ячменя, принимали за единицу, называвшуюся чакса; более крупной мерой веса были 2 чаксы — бир нимшек, или 12 килограммов, бир шимек —4 чакса, или 48 килограммов. Часто зерно измеряли более простым способом: брали 100 или 200 байсов зерна, засыпали в какой-нибудь сосуд и измеряли количество зерна по высоте от дна сосуда по суставам пальцев рук. В этом случае процесс измерения проходил намного быстрее, но неточность увеличивалась.
Количество зерна измерялось также кап — мешками, которые имели разную вместимость. Самый большой кап имел высоту в рост жеребенка и назывался тай кап; его вместимость была равна одному батману пшеницы или 12 пудам. В народных эпосах упоминаются богатыри, которые за один присест могли съесть не один батман зерна:
Хлебом пахнущий огромный Джолой.
Так что же такое объём?
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п.
В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от латинского volume — «объём», «наполнение».
За единицу измерения объема принимается куб, ребро которого равно единице измерения отрезков. Это кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр или даже кубический километр. Часто для измерения объёма жидкости используют единицу измерения 1литр. Схема перевода одной единицы измерения объема в другую приведена ниже.
Объёмы обладают следующими свойствами:
1. Объем тела есть неотрицательное число.
2. Равные тела имеют равные объемы
3. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.
Согласно третьему свойству, чтобы найти объём прямоугольного параллелепипеда, нужно разбить его на кубы с ребром, равным единице измерения. Но такой способ измерения объёмов неудобен, поэтому применяют формулу для вычисления объёма прямоугольного параллелепипеда V=abc. Формулы для вычисления других геометрических тел немного сложнее. Несмотря на это их надо знать уметь применять при решении математических задач и в жизни. В своей практической деятельности человек часто встречается с необходимостью вычисления объёмов, например, при изготовлении каких-либо деталей или при строительстве различных сооружений. Многие строительные объекты, детали конструкций и другие предметы имеют форму геометрических тел: параллелепипедов, призм, цилиндров, шаров.
Предлагаем таблицу, в которые вошли часто используемые геометрические тела и формулы нахождения их объема. Распечатайте и используйте!
Полезные ссылки
Проект "Самообразование" служит для представления знаний в понятной, ясной и краткой форме, удобной для восприятия человеком, не имеющим специальной подготовки в той или иной научной области. Здесь представлены задачи из открытого банка задач по ЕГЭ математика профильный уровень за предыдущие годы. Все задачи разбиты по темам и содержат подробное решение. Это поможет быстро сориентироваться в каталоге и выбрать для себя те темы, которые его интересуют. Вперед, к знаниям! http://self-edu.ru/math_egecats.php
Здесь вы найдете много полезных и нужных формул, таблиц и справочной информации. А онлайн калькулятор поможет рассчитать объем. Для расчета задайте необходимые данные. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров. Попробуем? http://mozgan.ru/Geometry#block1
Глоссарий
Геометрическое тело - это «то, что имеет длину, ширину и глубину» в «Началах» Евклида, а в учебниках элементарной геометрии - «часть пространства, ограниченная своей образуемой формой».
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости. Содержит углы, вершины, грани и ребра.
Конус - это тело, которое состоит из круга – основание конуса, точки, не принадлежащей плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса и точки окружности основания. Получается в результате вращения прямоугольного треугольника вокруг одного из катетов.
Куб – это прямоугольный параллелепипед с равными ребрами.
Параллелепипед – это четырехугольная призма, основаниями которой являются параллелограммы.
Пирамида - это многогранник, который состоит из многоугольника — основания пирамиды, и треугольников, имеющих общую вершину, называемых боковыми гранями пирамиды.
Призма - это многогранник, поверхность которого состоит из двух равных многоугольников и параллелограммов, имеющих общие стороны с каждым из оснований.
Тела вращения – это геометрические тела, полученные в результате вращения некоторой фигуры (обычно плоской) вокруг прямой.
Цилиндр — тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра. Получается в результате вращения прямоугольника вокруг одной из его сторон.
Шар - это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Получается в результате вращения полукруга вокруг его диаметра.
Библиография
- Архимед [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88903749, сохранённая в 10:33 UTC 10 ноября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL:https://ru.wikipedia.org/wiki/Архимед (дата обращения: 20.11.2017)
- ЕГЭ математика. Профильный уровень. Каталог заданий по темам. : [Электронный ресурс] // Самообразование. URL: http://self-edu.ru/math_egecats.php (дата обращения: 20.11.2017)
- Мозган Онлайн калькулятор. : [Электронный ресурс] // mozgan.ru. URL: http://mozgan.ru/Geometry#block1 (дата обращения: 20.11.2017)
- Системы измерения и счет у кыргызов.: [Электронный ресурс] //Open.kg Открытый Кыргызстан. URL: https://www.open.kg/about-kyrgyzstan/culture/ethnography/1970-sistemy-izmereniya-i-schet-u-kyrgyzov.html . (дата обращения: 20.11.2017)
- Как посчитать объем - формулы расчета. : [Электронный ресурс] // «ФБ», 2017. URL: http://fb.ru/article/143418/kak-poschitat-obyem---formulyi-rascheta (дата обращения: 20.11.2017)
- Загадки в стихах о геометрических фигурах и телах. : [Электронный ресурс] //Литературный проект "Ковдория" 2007 - 2012 URL: http://igri-uma.ru/forum/index.php?showtopic=3936 (дата обращения: 20.11.2017)
- Пирамида (геометрия) [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 85954734, сохранённая в 15:42 UTC 13 июня 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Пирамида_(геометрия) (дата обращения: 20.11.2017)
- Призма (геометрия) [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 87437416, сохранённая в 14:58 UTC 4 сентября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Призма_(геометрия) (дата обращения: 20.11.2017)
- Куб [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 88557583, сохранённая в 15:36 UTC 25 октября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Куб (дата обращения: 20.11.2017)
- Прямоугольный параллелепипед [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 87981530, сохранённая в 19:25 UTC 30 сентября 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL: https://ru.wikipedia.org/wiki/Прямоугольный_параллелепипед (дата обращения: 20.11.2017)
- Цилиндр [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 85933764, сохранённая в 15:46 UTC 12 июня 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL:http://ru.wikipedia.org/?oldid=85933764 (дата обращения: 20.11.2017)
- Конус [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 87095971, сохранённая в 10:39 UTC 16 августа 2017 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2017. URL:https://ru.wikipedia.org/wiki/Конус. URL:(дата обращения: 20.11.2017)
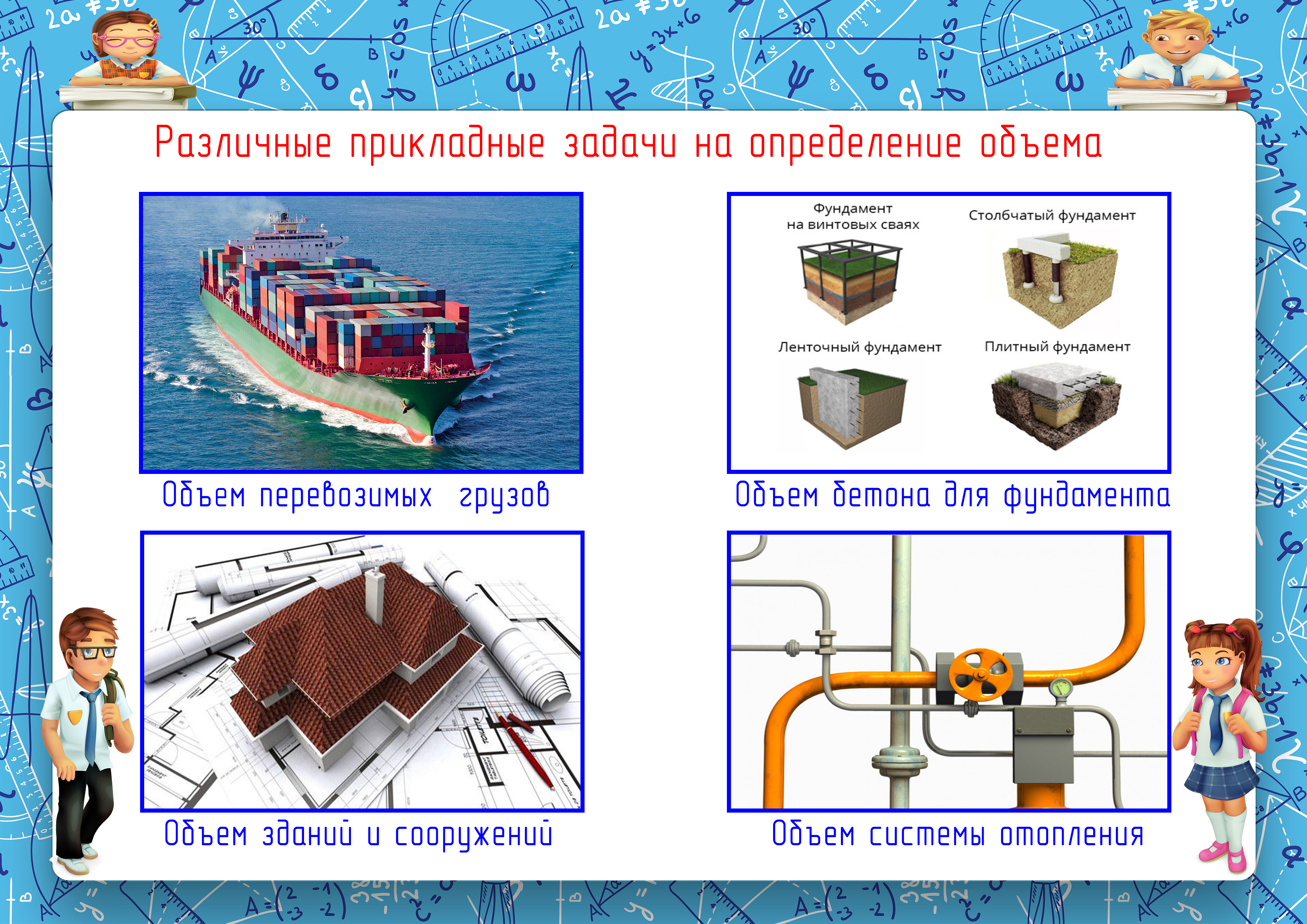
азличные прикладные задачи на определение объема.
Вернемся к проблеме: как посчитать объем перевозимых грузов. Каким является груз: фасованным или сыпучим? Каковы параметры тары? Вопросов больше, чем ответов. Немаловажным станет вопрос массы груза, поскольку транспорт отличается грузоподъемностью, а трассы – максимальным весом транспортного средства. Нарушение правил перевозки грозит штрафными санкциями.
Вопрос определения объемов играет немаловажную роль в строительстве. Возведение домов, других сооружений – дело затратное, стройматериалы требуют внимательного отношения и предельно точного расчета. Основа здания – фундамент - представляет собой обычно литую конструкцию, заполняемую бетоном. Перед тем как посчитать объем бетона, необходимо определить тип фундамента. Плитный фундамент – плита в виде прямоугольного параллелепипеда. Столбчатое основание - прямоугольные или цилиндрические столбы определенного сечения. Определив объем одного столба и умножив его на количество, можно рассчитать кубатуру бетона на весь фундамент. Рассчитывая объем бетона для стен или перекрытий, поступают достаточно просто: определяют объем всей стены, умножая длину на ширину и высоту, затем отдельно определяют объемы оконных и дверных проемов. Разность объема стены и суммарного объема проемов – объем бетона.
Некоторые прикладные задачи требуют знаний об объеме зданий и сооружений. К ним относятся проблемы ремонта, реконструкции, определения влажности воздуха, вопросы, связанные с теплоснабжением и вентиляцией. Прежде чем ответить на вопрос о том, как посчитать объем здания, делают замеры по внешней его стороне: площади сечения (длина умножается на ширину), высоты здания от нижней части первого этажа до чердака. Определение внутренних объемов отапливаемых помещений проводят по внутренним обводкам.
Современные квартиры и офисы невозможно представить без системы отопления. Основной частью систем являются батареи и соединительные трубы. Как посчитать объем системы отопления? Полный объем всех секций отопления, который указан на самом радиаторе, необходимо сложить с объемом труб. И на этом этапе встает проблема: как посчитать объем трубы. Представим, что труба – цилиндр, решение приходит само собой: используем формулу расчета объема цилиндра. В отопительных системах трубы заполняются водой, поэтому необходимо знать площадь внутреннего сечения трубы. Для этого определяем ее внутренний радиус. Формула определения площади круга известна из курса геометрии. Общая длина труб определяется по их протяженности в помещении.Вопрос: «Почему сложные загадки опасны для людей?»
Разгадывать загадки – очень увлекательное занятие. Ведь они учат думать и анализировать, расширяют знания о мире, пополняют словарный запас. Загадки прекрасно развивают мышление, логику, память. И делают это непринужденно, в игровой форме. Ведь искать разгадку так весело и интересно! Ну, а поскольку в таком состоянии думать тяжело, сразу приводим ответ, надо лишь немного подождать, чтобы его увидеть.
Многие из вас скажут, как же применять на практике геометрические формулы, если запомнить их очень сложно, а для некоторых это просто набор букв и цифр. В этом поможет мнемотехника: каждой или нескольким единицам информации «присваивается» образ, и далее связываются данные образы. Чтобы вспомнить (воспроизвести) данную информацию, порядок действия будет обратный: вспоминаются связанные между собой образы, а затем – то, что под ними подразумевалось. Таким образом, фактически сначала мы кодируем, зашифровываем данные в форму, удобную для запоминания, а когда они нам понадобятся, мы достаем их из памяти и расшифровываем. Звучит сложно? Тогда смотрим видео ролик «Как запомнить формулы объема»