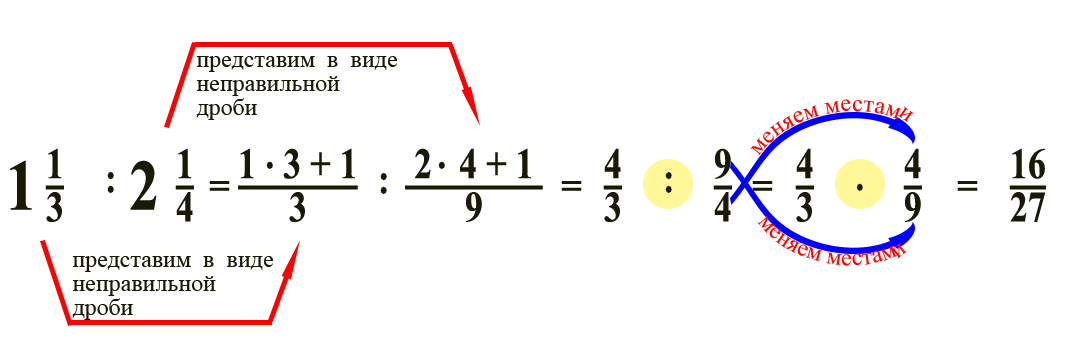Математика: Действия над обыкновенными дробями — различия между версиями
Msu05 (обсуждение | вклад) (→Старинные задачи на дроби) |
Msu05 (обсуждение | вклад) (→Библиография) |
||
| Строка 199: | Строка 199: | ||
<div class="shadow radius sbstyle" style="margin-top:20px;"> | <div class="shadow radius sbstyle" style="margin-top:20px;"> | ||
<div class="row"> | <div class="row"> | ||
| − | <div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;"> | + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">волшебные числа в произведениях народного творчества</div> |
</div> | </div> | ||
| − | + | Предлагаем вашему вниманию самые распространенные пословицы и поговорки с числами. Подумайте, какой смысл они несут. | |
{{center|[[Файл:В_тридевятом_цартсве.jpg|400px]]}} | {{center|[[Файл:В_тридевятом_цартсве.jpg|400px]]}} | ||
Версия 16:14, 22 мая 2018
Дроби можно складывать, вычитать, умножать и делить. Однако, операции сложения и вычитания зависят от знаменателей дробей.
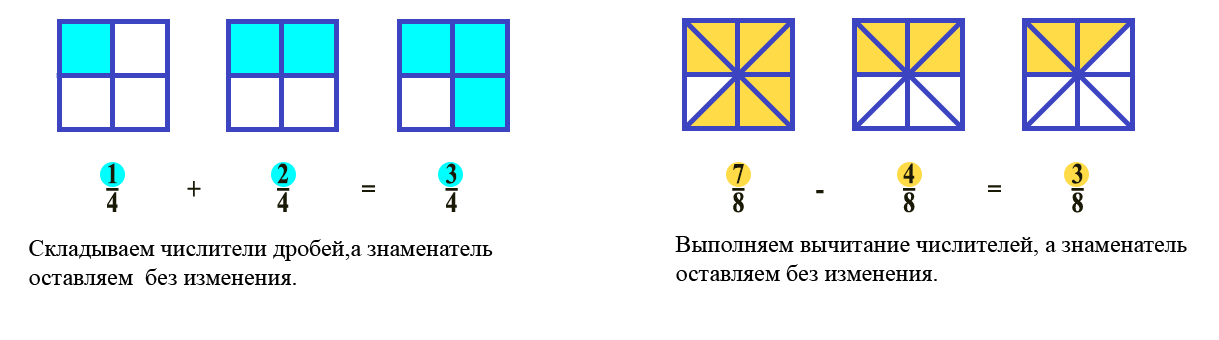
Сложение и вычитание обыкновенных дробей с одинаковым знаменателем
Для сложения или вычитания дробей с одинаковыми знаменателями достаточно сложить или вычесть их числители.
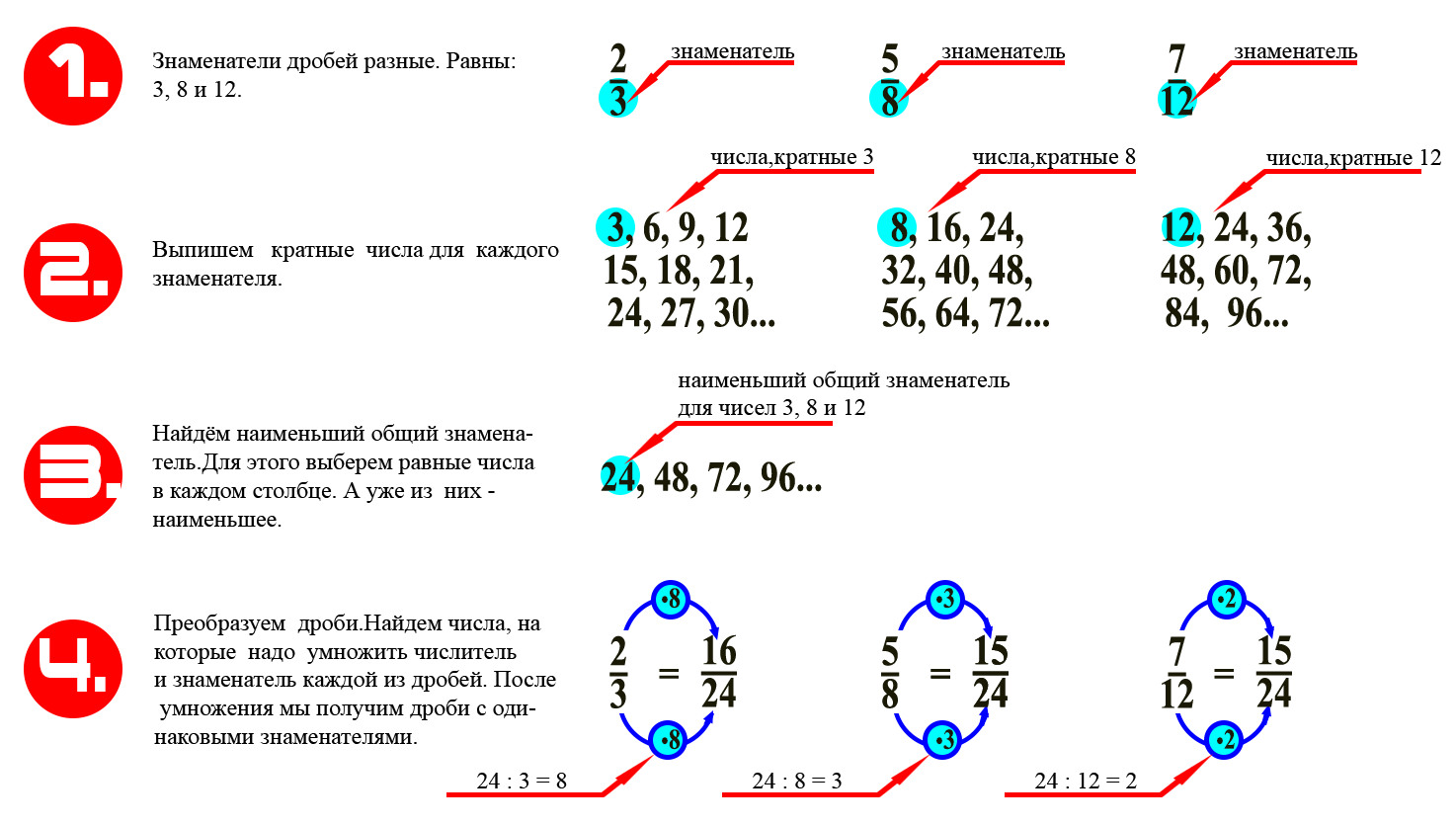
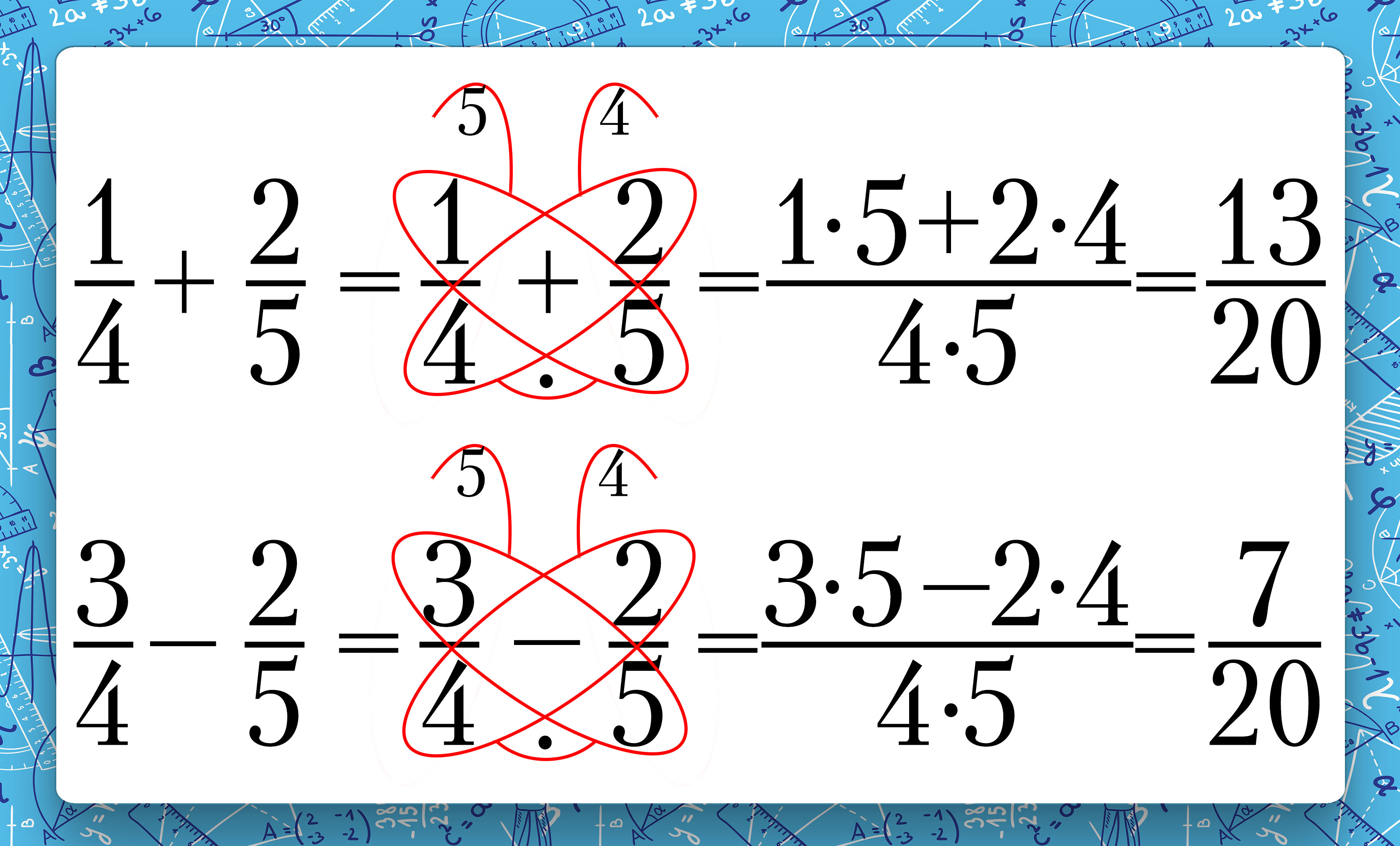
Сложение и вычитание обыкновенных дробей с разными знаменателями
Чтобы сложить или вычесть дроби с разными знаменателями, их нужно привести к общему знаменателю, а затем выполнить сложение или вычитание по предыдущему правилу.
Что же такое общий знаменатель? Общий знаменатель дробей – это такое число, которое делится нацело на каждый знаменатель исходных дробей.
Давайте попробуем привести к общему знаменателю три обыкновенных дроби.
Теперь, когда нам известно, как приводить дроби к общему знаменателю, попробуем решить примеры.
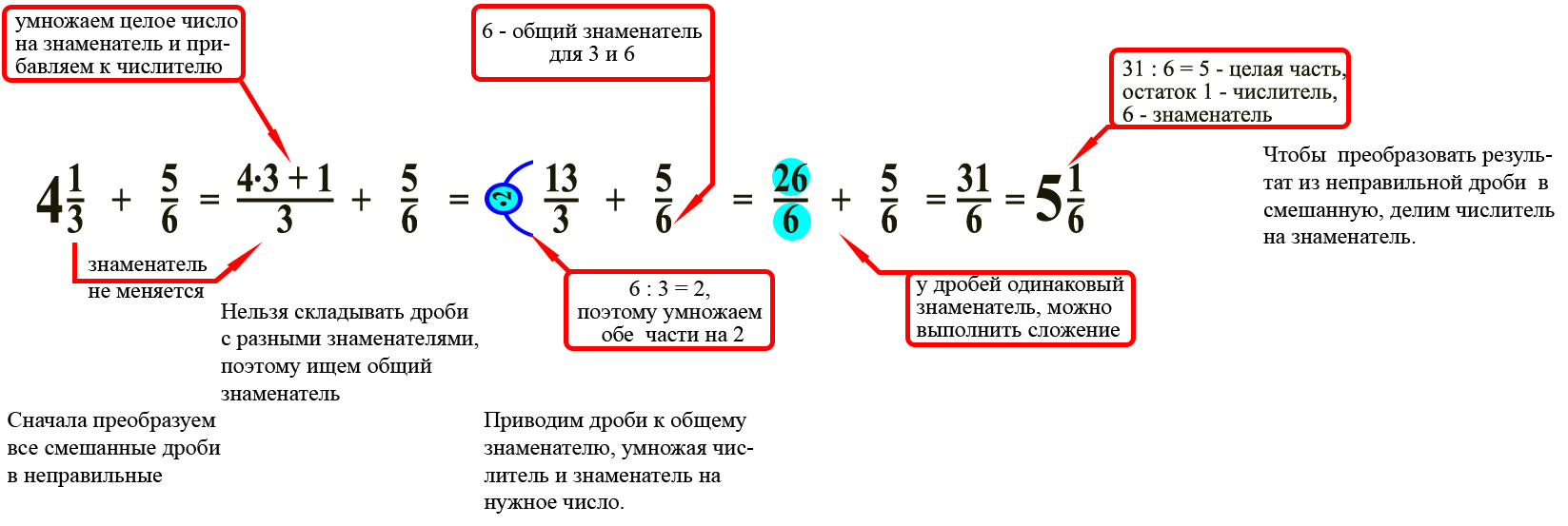
Пример 1. Выполните сложение дробей.
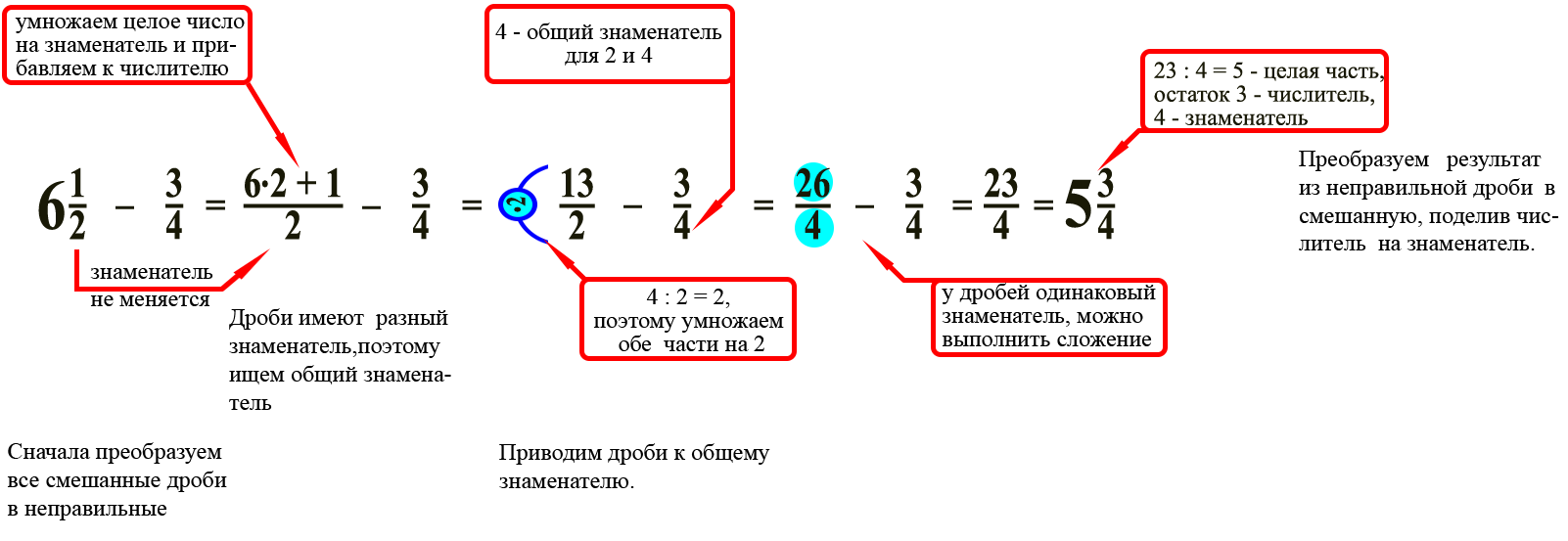
Пример 2. Выполните вычитание дробей.
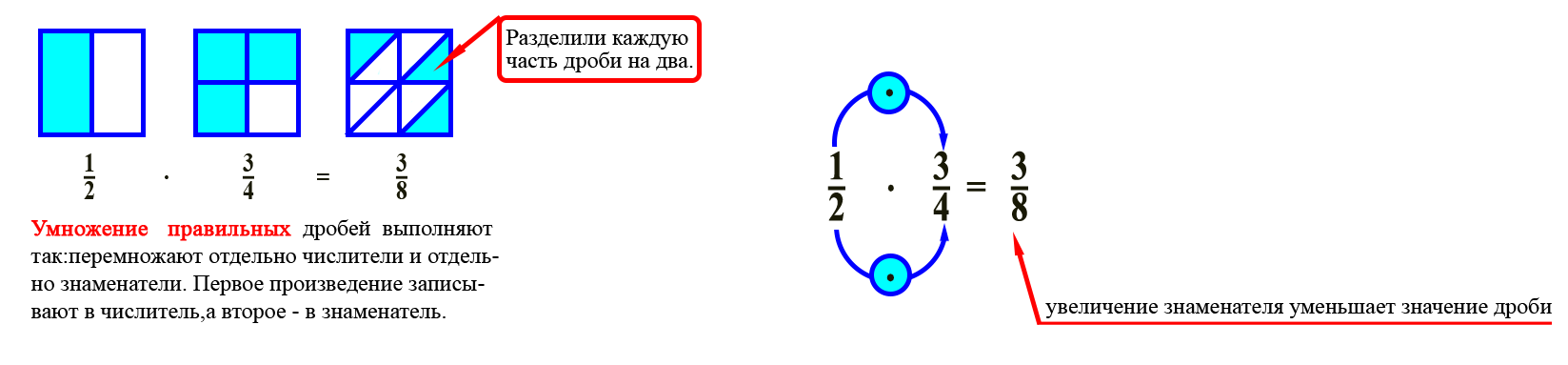
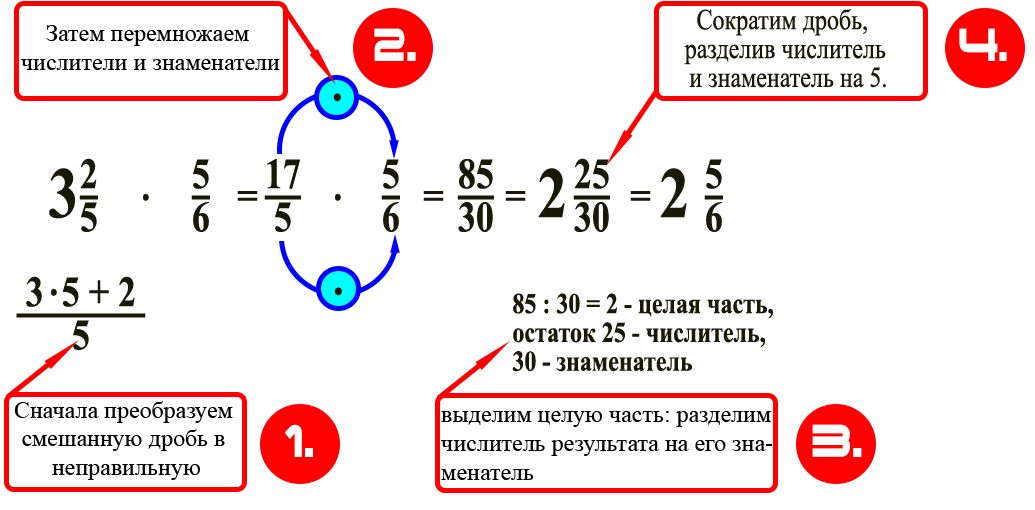
Умножение дробей
Чтобы умножить смешанную дробь на правильную, нужно сначала превратить ее в неправильную и выполнить умножение по предыдущему правилу.
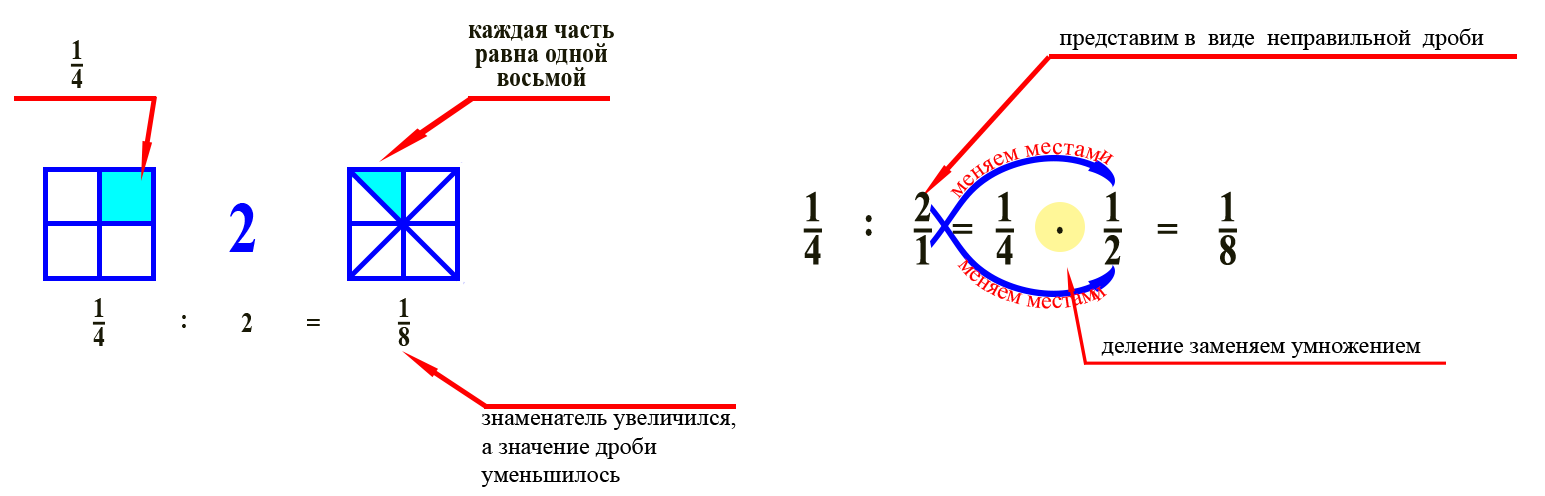
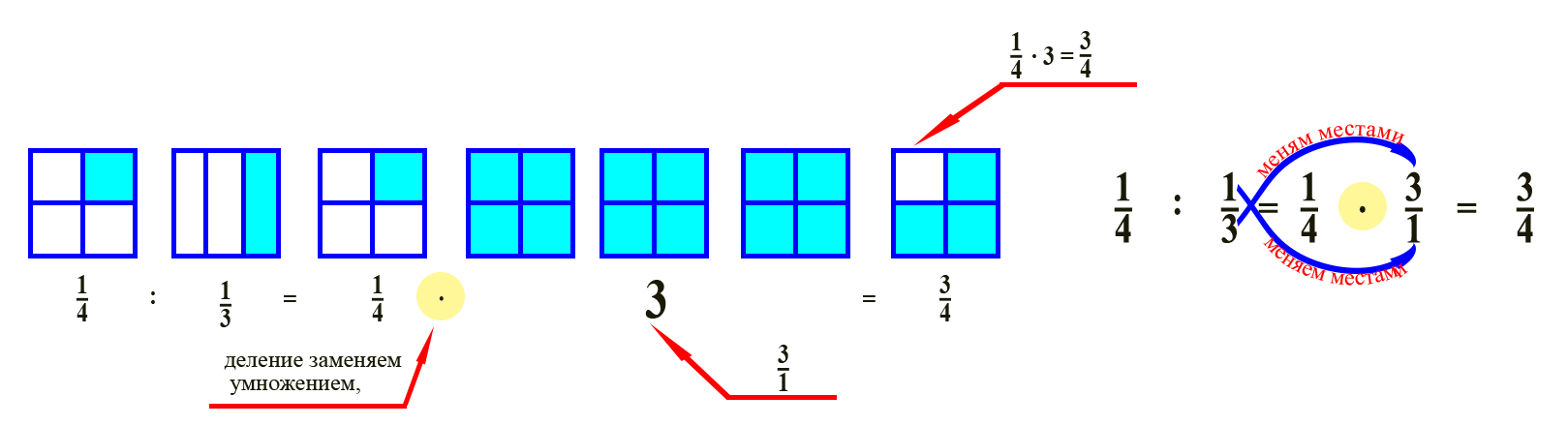
Деление дробей
Дроби можно делить. Рассмотрим сначала деление на целые числа. Для этого запишем целое число, как дробь, поменяем местами числитель и знаменатель и умножим на первую дробь. Это можно сделать в виду того, что деление дроби на целое число можно представить, как деление этой дроби на равные части.
Перейдем к делению правильных дробей. Для этого воспользуемся противоположной операцией – умножением.
В случае деления смешанных дробей сначала преобразуем их в неправильные дроби, а только затем выполним деление согласно предыдущему правилу.
Старинные задачи на дроби
В древних рукописях, старинных учебниках арифметики и даже в художественной литературе встречается очень много интересных задач на дроби. Решение каждой из них требует немалой смекалки и сообразительности, умения рассуждать. Давайте рассмотрим некоторые из них.
Глоссарий
Арифметическая прогрессия — последовательность чисел, в которой каждое последующее число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа.
Геометрическая прогрессия — последовательность чисел, в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число.
Дробь — это число, состоящее из одной или нескольких частей (долей) единицы.
Смешанные дроби – это дроби с целой частью.
Полезные ссылки
Дроби в математике используются для того, чтобы обозначать часть величины, которая рассматривается. Если речь идет о части, то обязательно есть и целое – то, от чего берется соответствующая часть. Зная целое, нужно уметь находить его часть, указанную соответствующей дробью, и наоборот, по известной части - целое. Подробнее смотри: «Задачи на нахождение части целого и целого по его части» : [Электронный ресурс] //Marianna L YouTube, 2017. URL:https://www.youtube.com/watch?v=dLG5CXJtJlE . (дата обращения 20 ноября 2017)
Библиография
- Варга Б., Димень Ю., Лопариц Э. Язык, музыка, математика М.: Мир, 1981. — 248 с.: ил.
- В.А. Гусев, А.Г. Мордкович Математика: Справочные материалы. Книга для учащихся. — 2-е изд. — М.: Просвещение, 1990. — 416 с.: ил.
- Видеоурок «Задачи на нахождение части целого и целого по его части. Часть 1»: [Электронный ресурс] //Marianna L YouTube, 2017. URL:https://www.youtube.com/watch?v=dLG5CXJtJlE . (дата обращения 20 ноября 2017)
- Метод бабочки. Сложение и вычитание дробей. : [Электронный ресурс] // Kid-mama, 2017. URL:http://kid-mama.ru/metod-babochki-slozhenie-i-vychitanie-drobej/. (дата обращения 20 ноября 2017)
очему на протяжении многих веков музыка так привлекательна для большинства людей? Почему она пленяет умы, организовывает, создает хорошее настроение или, наоборот, умиротворяет? Оказывается, музыкальные произведения соединяют, на первый взгляд, несовместимые вещи: высокие чувства и математический расчёт. В музыке, как и в математике есть счет, параллельность, последовательность, противоположность, симметрия. И благодаря этому мы можем услышать высокий и низкий звук, протяжное и отрывистое звучание, можем двигаться вверх и спускаться вниз по ступенькам звукоряда, напевая гаммы.
Остановимся более подробно на связи обыкновенных дробей и музыки.
В музыке постоянно надо считать: 7 нот, 5 линеек нотного стана, интервалы. А ноты все разные: одни коротенькие, другие длинные. При записи мелодии, звуки имеют свою длину - длительность. Здесь и происходит сопоставление целого числа и целой длительности, дробного числа и длительности коротких нот, записываемых при помощи дроби.
В музыке мы имеем дело с короткими и длинными длительностями, они составляют основу любого ритма: целая нота, половинная, одна четвертная, одна восьмая, одна шестнадцатая. Названия длительности служат одновременно и названиями чисел. Нетрудно понять, почему длительности музыкальных нот заимствовали свои названия у дробей. Мы видим, что длительности получаются так же, как дроби: они возникают при делении целой ноты на равные доли. Поэтому длительность можно подсчитывать как дробные числа (*).div>
Равенство здесь надо понимать в том смысле, что длительность слева равна сумме длительностей справа. С помощью чисел тоже равенство можно записать в различных видах. Если все длительности в музыкальном произведении увеличить вдвое, произведение надо исполнять медленнее и наоборот.
Интересно, что принцип построения длительностей соответствует принципам построения геометрической и арифметической прогрессиям.
Еще в Древней Греции математика и музыка назывались родными сёстрами, а со времён Пифагора наука о музыке входила в пифагорейскую систему знаний, наряду с арифметикой (наукой о числах), геометрией (наукой о фигурах и их измерений) и астрономией (наукой о строении Вселенной).
Изучая высоту звука с помощью монохорда – простейшего инструмента Древних греков, состоящего из одной струны, резонаторного ящика и передвижной подставки, с помощью которой можно было изменять длину натянутой струны, Пифагор обнаружил поразительные вещи. Выяснилось, что приятные слуху созвучия – консонансы получаются лишь в том случае, когда длины струн, издающих эти звуки, соотносятся как целые числа первой четвёрки, т.е 1:2, 2:3, 3:4. Это открытие потрясло Пифагора: оказалось, что звук и созвучие могут быть описаны простыми числами.
Пифагорейцы открыли «золотую пропорцию» – «точку золотого сечения», которое в музыке определяла точное место кульминации.
Демокрит, наблюдая за игрой на музыкальных инструментах, установил, что высота тона звучащей струны меняется от ее длины. Исходя из этого, он определил, что интервалы музыкальной гаммы могут быть выражены отношением простых целых чисел.
Исследованию музыки посвящали свои работы многие величайшие математики, такие как: Рене Декарт (его первый труд - “Compendium Musicae” в переводе “Трактат о музыке” ), Готфрид Лейбниц, Христиан Гольдбах, Жан Д’Аламбер, Даниил Бернулли.
Композиторы часто признаются, что их метод немногим отличается от математического. О том же пишет выдающийся дирижер Эрнест Ансерме: «Между музыкой и математикой существует безусловный параллелизм. И та и другая представляют собой действие в воображении, освобождающее нас от случайностей практической жизни». Многие выдающиеся музыканты блистали математической одаренностью: только что упомянутый Эрнест Ансерме – профессиональный математик и лучший исполнитель Стравинского, Леонид Леонидович Сабанеев – выпускник математического факультета Московского университета, прекрасный пианист, композитор и друг Скрябина. Выдающийся виолончелист Карл Юльевич Давыдов закончил физико-математический факультет, и как вспоминают современники, имел «блистательные способности к чистой и прикладной математике: в квартире его долго сохранялась модель железнодорожного моста, им изобретенного и, по словам специалистов, вполне достойного внимания». </p>
Интересные факты из жизни известных музыкантов
Николай Андреевич Римский-Корсаков - русский композитор, педагог, дирижёр, общественный деятель, музыкальный критик - учился в Школе математики и навигации в Санкт-Петербурге. Директор школы считал, что уроки музыки помогут Николаю стать менее застенчивым. Сам Римский-Корсаков писал, что был безразличен к урокам, но любовь к музыке стала проявляться после посещений оперы и концертов оркестров.
Альбер Шарль Поль Мари Руссель — известный французский композитор первой трети XX века - начал заниматься музыкой в 25. Изначально он интересовался математикой, провел семь лет во французском флоте в качестве мичмана. Позже он довольно долго служил на корабле в Юго-восточной Азии и ушел в отставку в 25 лет. Именно в это время он серьезно заинтересовался музыкой. Точнее — изучением гармонии.
Арам Ильич Хачатурян - советский композитор, дирижёр, музыкально-общественный деятель, педагог - начал серьезно заниматься музыкой в 19 лет. Хачатурян еще в школе играл на фортепиано, горне и тубе, но родители не были в восторге от этого увлечения. После школы он даже поступил на физико-математическй факультет. Но Араму хватило терпения ненадолго. Уже спустя год он учился в Гнесинском музыкальном училище, где занимался на виолончели и фортепиано, брал уроки композиции.
Брайан Мэй - гитарист «Queen» - окончил физико-математический факультет престижнейшего Имперского колледжа Лондона. Брайан уже почти подготовил диссертацию на соискание степени доктора философии по астрономическим исследованиям в инфракрасном диапазоне и имел две научные публикации по астрономии, когда успех «Queen» заставил его прервать научную карьеру.
Однако впоследствии он вернулся к исследовательской деятельности и завершил начатое, получив степень в Хертфордширском университете. 14 апреля 2008 года музыкант был назначен ректором Ливерпульского университета имени Джона Мурса и занимал эту должность до марта 2013 года. В данный момент Брайан продолжает музыкальную карьеру в группе «Queen» и продолжает научную деятельность в области теоретической физики и математики.
Существуют определенные математические закономерности, на которых построено множество трюков с отгадыванием задуманного числа. Но эти закономерности можно использовать не только ради шутки или загадки, а там, где действительно нужно быстро сосчитать, а под рукой нет никакого гаджета, способного помочь в этой ситуации. Итак, перед вами «Метод бабочки» для быстрого сложения и вычитания обыкновенных дробей с разными знаменателями.