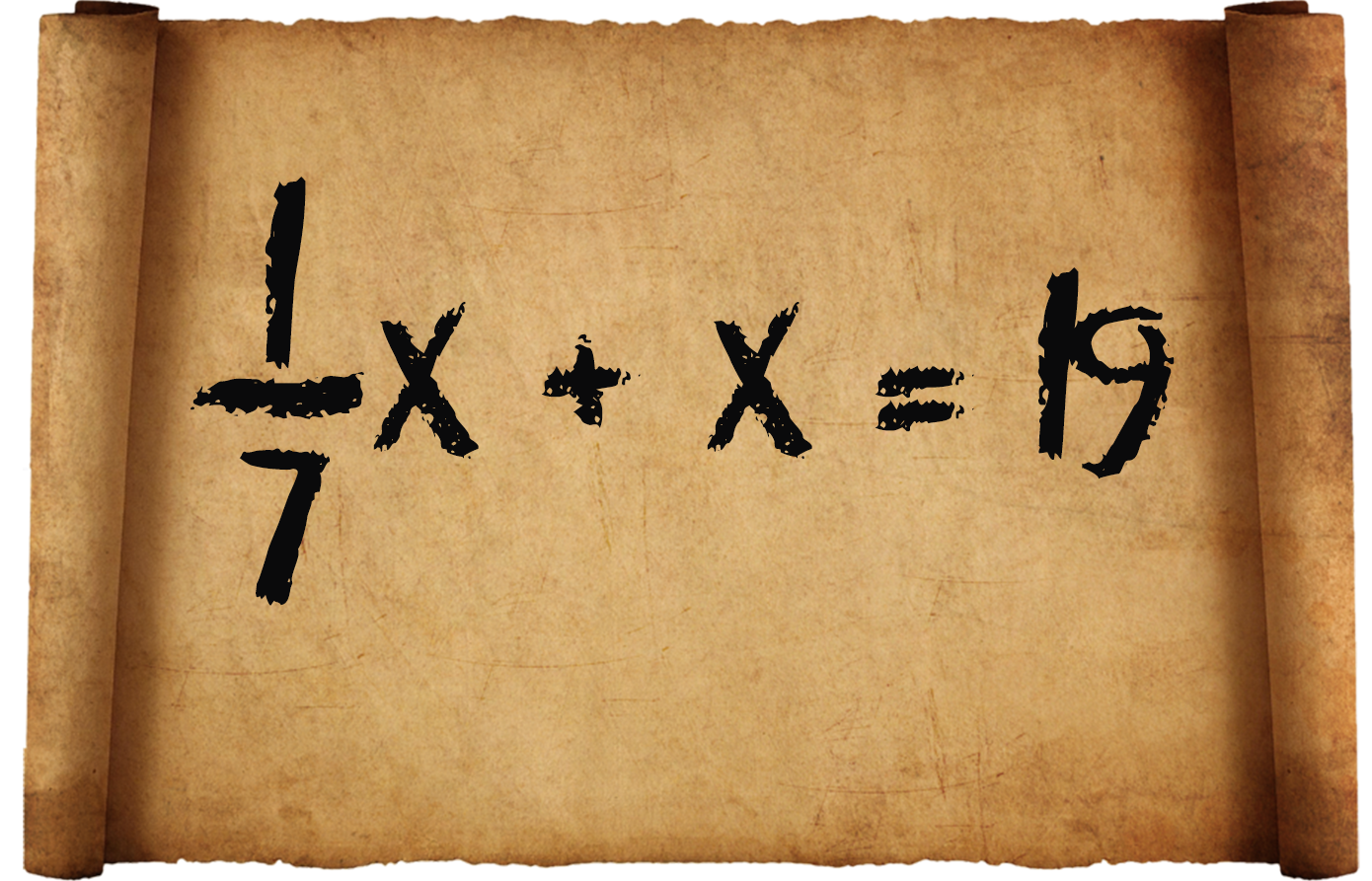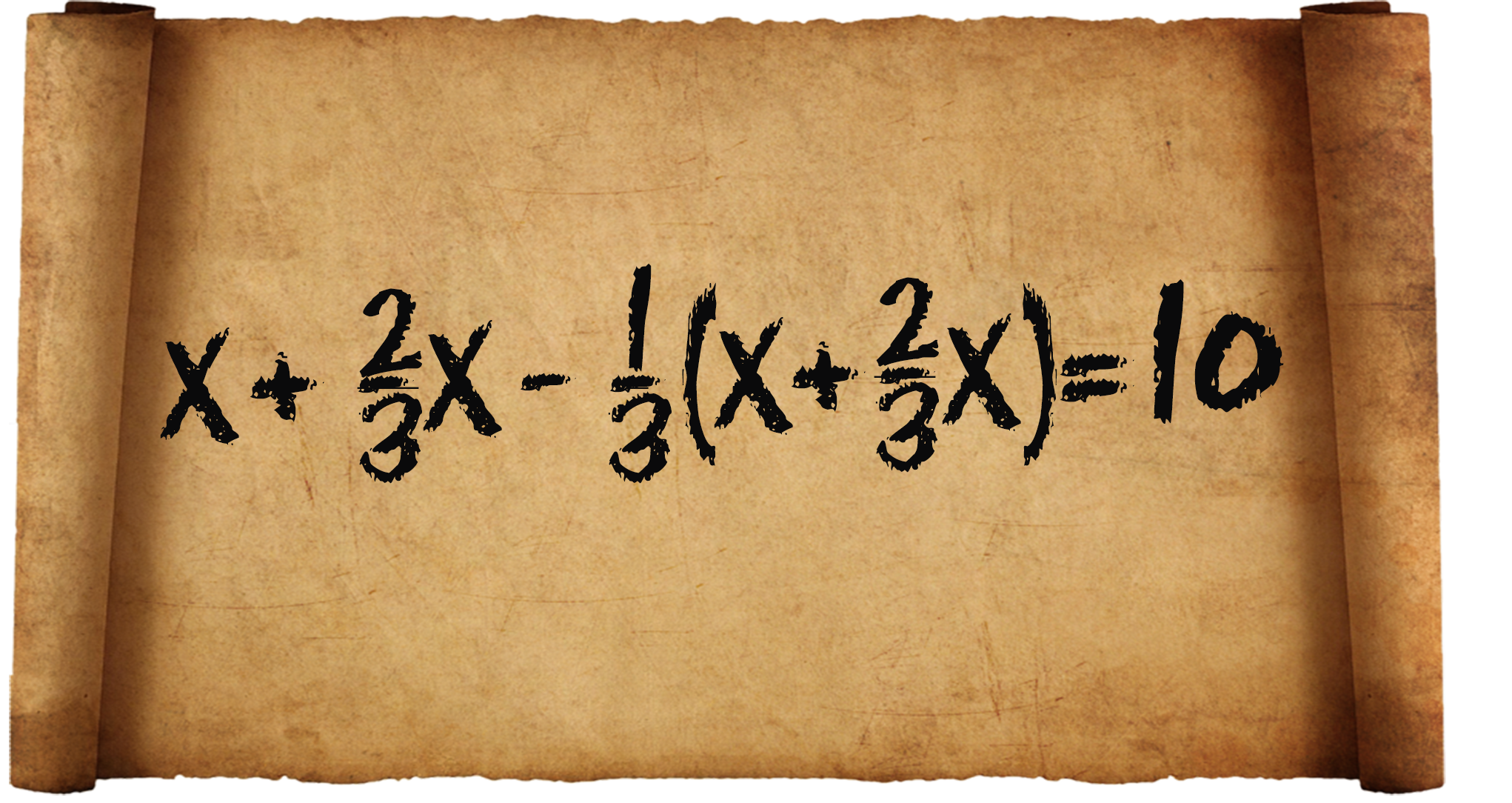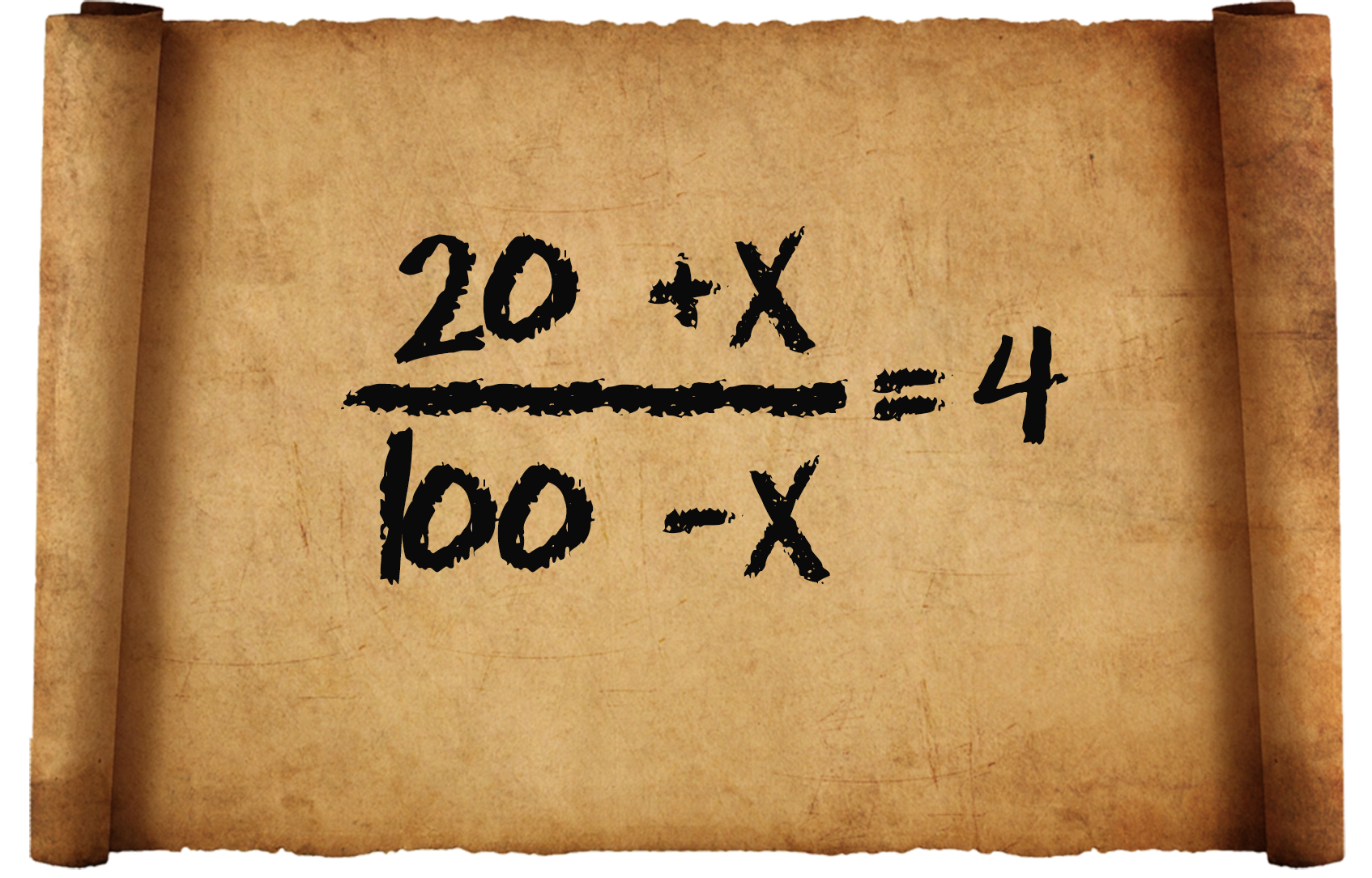Математика: Теңдемелердин чыгарылышы — различия между версиями
Msu05 (обсуждение | вклад) |
Msu05 (обсуждение | вклад) |
||
| Строка 65: | Строка 65: | ||
Бул жерден х ти табуу оңой болот. x=4 | Бул жерден х ти табуу оңой болот. x=4 | ||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:Важнейшие_факты_из_истории_уравнений_—_к._т..mp4|500px]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Важнейшие_факты_из_истории_уравнений_—_к._т..mp4|500px]]}}</div> |
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | ||
Версия 08:29, 4 мая 2018
Эң байыркы математикалык жазылмаларда эле амалдардын жардамы менен чыгарылган мисалдар жана амалдар кездешкен. Мындай Египеттик папируста биздин заманга чейин 2000 жыл мурун ( анда автор Ахмес жазгыч көрсөткөндөй, бул математикалык жазылмалар мындан да байыркы башка жазылмалардын көчүрмөсү) белгисиз санды табууга маселелер болгон. Ал белгисиз «хау» (дөбөчө) деп аталган жана өзгөчө иероглиф менен белгиленген.
Мына ал папирустун мисалдарынын чыгарылыштарынан:
1) 1) «Белгисиз, анын жетинчи бөлүгү, анын бүтүнү 19ду тузөт».
Азыркы кезде бул мисал мындайча жазылат:
2) «![]() кошулган жана
кошулган жана ![]() алынган: калдыгы 10».
Папируста маселенин чыгарылышын мындайча түшүнсө болот: белгисизге
алынган: калдыгы 10».
Папируста маселенин чыгарылышын мындайча түшүнсө болот: белгисизге ![]() тү кошуп, андан
тү кошуп, андан ![]() алынган, келип чыккан суммадан; калдыгы 10; санды табуу керек.
Азыркы кезде бул маселе мындайча жазылат:
алынган, келип чыккан суммадан; калдыгы 10; санды табуу керек.
Азыркы кезде бул маселе мындайча жазылат: ![]() ; Жообу: х=9
; Жообу: х=9
3) Диофантада дагы бир белгисизи менен амалдар кездешет, мисалы: “20 жана 100 сандары. Бир эле санды эң кичине санга кошуп жана эң чоңунан алуу; сумманын айырмага карата мааниси 4 кө барабар”.
4) Индиялыктардын биздин заманга чейинки VII жана VIII кылымдардагы арифметикалык кол жазмаларында, ал дагы андан дагы байыркы (III-IVкылымдардагы) кол жазманын көчүрмөсү, анда мындай маселе бар:
“Төрт курмандыктын экинчиси биринчиге караганда экиге көп берди, үчүнчүсү экинчиге караганда үчкө көп, төртүнчү үчүнчүдөн төрткө көп, баары биригип 132 беришти. Биринчи канчаны берди?”
Теңдемени жазсак: x+2x+6x+24x=132
Кол жазмаларда бул маселе “жалган абал” ыкмасы менен чыгарылат. (Бул ыкманы Л.Ф.Магницкий өзүнүн “Арифметикасында” пайдаланган.)
“Эгерде биринчи 1ди берсе, анда экинчи 2ни, үчүнчү 6, төртүнчү 24, баары чогуу 33. Бирок баары бирге 132 болчу да, башкача айтканда төрткө көп. Демек, ар бир курмандык төрткө көп беришкен”. Жооп: 4;8;24;96.
Бирок биринчи даражадагы бир белгисизи менен теңдемени чыгаруунун жалпы эрежесин IX кылымда Мухаммед аль-Хорезми берген.
Өзүнүн “Аль-джебр жана аль-мукабала” аттуу жазылмаларында ал теңдемени чыгаруудагы колдонулган эки абалды берген:
1) “аль-джебр” абалы, эгерде теңдемеде терс (алынуучулар) мүчөсү болсо, анда аларды теңдеменин эки жагынын тең карама-каршы мүчөлөрүнө кошулат, анда теңдеменин баардык мүчөлөрү оң болот.
2) “аль-мукабала” теңдеменин эки жагынан тең бирдей мүчөсү алынат, бул болсо аны жөнөкөйлөткөнгө алып келет.
Мисалы, Берилди: 5х-17=2х-5.
“аль-джебрды” пайдалансак: теңдеменин ар бир бөлүгүнө 5 менен 17и кошобуз.
Анда: 5х+5= 2х+17 алабыз.
“аль-мукабала”: Ар бир бөлүктөн 2х менен 5 ти алабыз.
Анда: 3х=12 ни алабыз.
Бул жерден х ти табуу оңой болот. x=4
Развитие математической науки в Кыргызстане
Математика как школьный предмет начала изучаться в Кыргызстане только после Октябрьской революции, а высшая математика - после открытия первого в Кыргызстане ВУЗа - Кыргызского государственного педагогического института - ныне Кыргызского национального университета им. Ж. Баласагына.
Систематические исследования по математике в Кыргызстане начались в 1940 году, на семинаре под руководством профессора Г.А. Сухомлинова. В 1949-1965 годы семинаром руководил профессор Я.В. Быков, ставший в 1960 году членом-корреспондентом АН Киргизской ССР, с 1966 г. этот семинар, ставший уже общереспубликанским, в стенах Института возглавил М.И. Иманалиев, академик АН Киргизской ССР (1979) и член-корреспондент АН СССР (1981 год).
В 1955 году был организован Отдел физики, математики и механики при Президиуме АН Киргизской ССР, в составе которого были, тогда еще кандидаты наук, Я.В. Быков и М.И. Иманалиев. В 1960 году Отдел был преобразован в Институт физики, математики и механики. В 1962 году он стал называться Институтом физики и математики, а в 1984 году на базе математических лабораторий Института физики и математики был организован Институт математики. На его базе в 2008 году был создан Институт теоретической и прикладной математики, а с 11 мая 2017 года он переименован в Институт математики НАН КР.
С 1984 года по 2016 год Институтом руководил академик М.И. Иманалиев, с 2016 года по настоящее время руководителем Института является академик А.А. Борубаев.
Деятельность Института определяется следующими основными направлениями научных исследований:
- Равномерные и топологические пространства и их отображения.
- Функциональные пространства.
- Динамические системы, описываемые разностными, дифференциальными и интегро-дифференциальными уравнениями, в том числе сингулярно-возмущенными.
- Интегральные уравнения, некорректные и обратные задачи.
- Оптимизационные экономические задачи.
- Компьютеризация научных исследований, интерактивное представление объектов.
Особое внимание уделяется исследованию по теории и приложениям интегро-дифференциальных, интегральных и дифференциальных уравнений, операционному исчислению, по разностным и суммарно-разностным уравнениям, математической физике, линейной алгебре. Больших успехов математика Кыргызстана достигла в области интегро-дифференциальных уравнений. Ученые математики надеются, что в математическую науку придут образованные, высокоинтеллектуальные, целеустремленные молодые люди и поднимут престиж математической науки Кыргызстана еще выше.
Уравнение. Корни уравнения
Равенство с переменной называют уравнением.
Каждое значение переменной, при котором данное уравнение превращается в верное равенство, называется корнем уравнения. Решить уравнение - это значит найти все его корни или доказать, что их нет. Уравнение может иметь один, два, несколько, множество корней или не иметь их вовсе.
Пример 1. Уравнение 5 + x = 15 имеет единственный корень x = 10, так как только при этом значении переменной 5 + x = 15 является верным равенством.
Пример 2. Уравнение (5 + x)(x - 6)=0 имеет два корня: -5 и 6.
Пример 3. 9 + x2 = 0 не имеет корней на множестве вещественных чисел.
Линейные уравнения
Линейным уравнением с одной переменной х называют уравнение вида ax = b, где a, b –вещественные числа; а называют коэффициентом при переменной, b - свободным членом.
Равносильность уравнений
Уравнения, имеющие одни и те же корни, называются равносильными уравнениями. Равносильными считаются и уравнения, у которых нет корней.
Пример 4. Уравнения x + 5 = 7 и x - 8 = -6 равносильны, так каждое из них имеет единственный корень, равный 2.
Пример 5. Уравнения 9 + x2 = 0 и 3x2 + 27 = 0 равносильны, так как каждое из них не имеет корней.
Пример 6. Уравнения 9 - x2 = 0 и x + 4 = 7 неравносильны, так как первое уравнение имеет два корня: 3 и -3, а второе только один корень: 3.
Когда уравнение решают, его стараются заменить на более простое, равносильное данному. Поэтому необходимо знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.
Теорема 1. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.
Например, уравнение x2 + 4 = 2x равносильно уравнению x2 + 4 - 2x = 0.
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Например, уравнение (x-5)/4 =4x равносильно уравнению x-5=16x.Обе части первого уравнения умножили на 4.
Рассмотрим на примерах решение уравнений.
Зачем нужны уравнения
Вычислительные задачи бывают прямые и косвенные. Решение первых диктуется самим условием задачи, а из условия косвенной задачи не видно, какие действия приведут к ее решению. При так называемом арифметическом решении нужно проявить подчас большую изобретательность, чтобы наметить план решения косвенной задачи. Каждая новая задача требует создания нового плана. Для рационализации вычислительного процесса и был создан метод уравнений, который является основным предметом изучения в алгебре. Таким образом, уравнения нужны для того, чтобы механизировать процесс вычисления. После того как уравнение составлено, решение его можно получить вполне автоматически. Вся трудность решения задачи сводится лишь к составлению уравнения.
Составить уравнение – это значит выразить в математической форме связь между известными задачи и неизвестными ее величинами.
Рассмотрим решение задач с помощью уравнений.
Задача 1. Мама в два раза старше сына. Десять лет назад она была старше сына в три раза. Сколько лет маме?
Задача 2. В трех коробках лежит 56 карандашей. Известно, что в первой коробке их в два раза больше, чем во второй, и в 2,5 раза меньше, чем в третьей коробке. Сколько карандашей в каждой коробке?
Задача 3. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.
Полезные ссылки
Первоначальные способы решения уравнений были достаточно сложными и разнообразными. В процессе развития математики произошло их значительное упрощение, и для каждого типа уравнений появился единый алгоритм решения. Более подробно можете увидеть: [Электронный ресурс] // novykrug YouTube, 2018. URL:https://www.youtube.com/watch?v=WpwOQHVB5s4 (дата обращения: 28. 04. 2018)
Математическая модель - это способ описания реальной жизненной ситуации (задачи) с помощью математического языка. На нашем этапе изучения алгебры мы будем использовать математическое моделирование, как помощь в решении задач.:[Электронный ресурс] // school-assistant.ru © 2016 URL: http://school-assistant.ru/?predmet=algebra&theme=matemat_model (дата обращения: 28. 04. 2018)
Применение линейных уравнений очень распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Линейные уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Линейное уравнение представляет собой алгебраическое уравнение, полная степень многочленов которого равна единице. Существует множество способов решения данных уравнений. Чтобы решить уравнения данного рода необходимо найти значение переменной.:[Электронный ресурс] // © Pocket Teacher. https://pocketteacher.ru/linear-equations-2-ru (дата обращения: 28. 04. 2018)
Глоссарий
- Алгебра – это раздел математики, который изучает общие свойства действий над различными величинами и решение уравнений, связанных с этими действиями.
- Веще́ственное число (от лат. realis — действительный) — математический объект, возникший из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких вычислительных операций, как извлечение корня, вычисление логарифмов, решение алгебраических уравнений, исследование поведения функци
- Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
- Теоре́ма (др.-греч. θεώρημα — «доказательство, вид; взгляд; представление, положение») — утверждение, выводимое в рамках рассматриваемой теории из множества аксиом посредством использования конечного множества правил вывода.
- Теорема Виета: сумма корней приведенного квадратного уравнения x2+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену: x1+x2=-p; x1∙x2=q.
Библиография
- Математическая модель. Правила http://school-assistant.ru/?predmet=algebra&theme=matemat_model
- Основные математические знаки и символы: [Электронный ресурс] // 2013-2018 «SYL.ru» URL: https://www.syl.ru/article/327248/osnovnyie-matematicheskie-znaki-i-simvolyi (дата обращения: 26. 04. 2018)
- Институт математики.:[Электронный ресурс] // 2016-2017 Национальная академия наук КР URL:http://naskr.kg/index.php/ru/struktura-nan-kr/nauchno-issledovatelskie-uchrezhdeniya/institut-matematiki (дата обращения: 28. 04. 2018)
- Линейное Уравнение - Решение С Помощью Онлайн Решателя:[Электронный ресурс] // © Pocket Teacher. https://pocketteacher.ru/linear-equations-2-ru (дата обращения: 28. 04. 2018)
- Развитие математической науки Кыргызстана:[Электронный ресурс] //2018 © Институт Математики URL: http://math.aknet.kg/home/science-develop.pdf
- В.А. Гусев, А.Г. Мордкович Математика. Справочные материалы М.: Просвещение, 1988.
- Федин С. Н. Математики тоже шутят. — 4-е изд. — М.: УРСС, 2012. — 216 с.
Знаки плюса и минуса придумали в немецкой математической школе алгебраистов. Они используются в «Арифметике» Иоганна Видмана (Johannes Widmann), изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов не ясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа практически мгновенно получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. В конце XVII века Лейбниц заменил крестик на точку, чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).
Знаки деления. Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл в середине XVII века.
Знак равенства предложил Роберт Рекорд 1510—1558) в 1557 году. Он пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. В континентальной Европе знак равенства был введён Лейбницем.
Знак «не равно» впервые встречается у Эйлера.Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше, меньше. Символы нестрогого сравнения предложил Джон Валлис. Первоначально черта была выше знака сравнения, а не под ним, как сейчас.
Математика – как высокая винтовая лестница,
чтобы взойти по ней к вершинам знаний,
надо пройти каждую ступеньку от первой до последней.
Американский математик Джордж Бернард Данциг , будучи аспирантом университета, однажды опоздал на урок и принял написанные на доске уравнения за домашнее задание. Оно показалось ему сложнее обычного, но через несколько дней он смог его выполнить. Оказалось, что он решил две «нерешаемые» проблемы в статистике, над которыми бились многие учёные.
Школьник зашел в лавочку возле школы. На прилавке лежали ручки по 30 рублей за штуку и карандаши по 15 рублей. Мальчик приобрел один карандаш и пошел к выходу, но по дороге подумал: «Я уже отдал продавцу 15 рублей, значит, если вернуть покупку, в сумме на моем счету окажется 30 руб». Сможет ли школьник теперь купить ручку? Почему?
Ответ
Не сможет.
В качестве объяснения приведем небольшую шутку.
Студент заказал в кафе булочку, но затем решил, что не слишком голоден и обменял ее на чашечку кофе. Выпив напиток, он направился к выходу, не расплатившись. Cамо собой, за ним побежала буфетчица.
- Вы не заплатили за кофе!
- Да, все верно, но я же взял его взамен булочки!
- Так булка тоже не оплачена!
- Верно, но я ведь ее и не ел!
2. Перед вами неверное неравенство 7+4-4=0.Как, переложив одну спичку, сделать его правильным?
3. Реши кроссворд.
По горизонтали.
4. Равенство двух отношений.
5. Французский математик, который установил связь между коэффициентами уравнения и его корнями.
По вертикали.
1. Значение переменной в уравнении.
2. Равенство, содержащее переменную.
3. Уравнение вида ax=b.
4. Неизвестное число в уравнении.