Математика: Основы комбинаторики — различия между версиями
Msu05 (обсуждение | вклад) (→Задачи) |
Msu05 (обсуждение | вклад) |
||
| Строка 11: | Строка 11: | ||
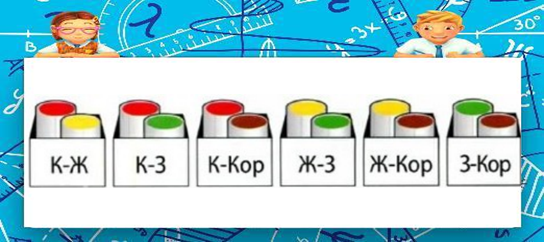
До начала расчетов необходимо навести порядок. Конечно же, мы не имеем в виду порядок на рабочем месте. Необходимо упорядочить объекты, число комбинаций с которыми мы хотим выяснить. Допустим, у нас есть банки с краской четырех цветов: красной (К), желтой (Ж), зеленой (3) и коричневой (Кор), и нам нужно разложить их по коробкам, по две разные банки в каждой. Мы можем сделать это следующим образом: | До начала расчетов необходимо навести порядок. Конечно же, мы не имеем в виду порядок на рабочем месте. Необходимо упорядочить объекты, число комбинаций с которыми мы хотим выяснить. Допустим, у нас есть банки с краской четырех цветов: красной (К), желтой (Ж), зеленой (3) и коричневой (Кор), и нам нужно разложить их по коробкам, по две разные банки в каждой. Мы можем сделать это следующим образом: | ||
| − | <div class="show-for-large-up">{{center|[[Файл:К_ж.png| | + | <div class="show-for-large-up">{{center|[[Файл:К_ж.png|500px]]}}</div> |
<div class="hide-for-large-up">{{center|[[Файл:К_ж.png|400px]]}}</div> | <div class="hide-for-large-up">{{center|[[Файл:К_ж.png|400px]]}}</div> | ||
то есть шестью различными способами, так как если в одной коробке находятся банки с желтой и красной красками, то она полностью идентична той, где лежат банки с красной и желтой. Но если мы хотим парными цветами раскрасить флаги, то сделать это можно будет так: то есть двенадцатью способами, так как красно-желтый флаг не является идентичным желто-красному. | то есть шестью различными способами, так как если в одной коробке находятся банки с желтой и красной красками, то она полностью идентична той, где лежат банки с красной и желтой. Но если мы хотим парными цветами раскрасить флаги, то сделать это можно будет так: то есть двенадцатью способами, так как красно-желтый флаг не является идентичным желто-красному. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Флаг.png| | + | <div class="show-for-large-up">{{center|[[Файл:Флаг.png|500px]]}}</div> |
<div class="hide-for-large-up">{{center|[[Файл:Флаг.png|400px]]}}</div> | <div class="hide-for-large-up">{{center|[[Файл:Флаг.png|400px]]}}</div> | ||
Вся наша жизнь состоит из множества разнообразных программ. Чтобы запустить ту или иную программу нужно ввести соответствующий верный пароль. В качестве кода в зависимости от рода программы могут выступать всевозможные цифры, слова или комбинации слов, поведение или действие. Комбинаторика используется в музыке, в мебельной деятельности, в различных играх (нарды, шашки, шахматы) и т.д. Читайте подробнее: http://ya-znau.ru/znaniya/zn/80, а если Вы хотите порешать задачки, то переходите сюда: http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html | Вся наша жизнь состоит из множества разнообразных программ. Чтобы запустить ту или иную программу нужно ввести соответствующий верный пароль. В качестве кода в зависимости от рода программы могут выступать всевозможные цифры, слова или комбинации слов, поведение или действие. Комбинаторика используется в музыке, в мебельной деятельности, в различных играх (нарды, шашки, шахматы) и т.д. Читайте подробнее: http://ya-znau.ru/znaniya/zn/80, а если Вы хотите порешать задачки, то переходите сюда: http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Области_применения.png| | + | <div class="show-for-large-up">{{center|[[Файл:Области_применения.png|500px]]}}</div> |
<div class="hide-for-large-up">{{center|[[Файл:Области_применения.png|400px]]}}</div> | <div class="hide-for-large-up">{{center|[[Файл:Области_применения.png|400px]]}}</div> | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Правила_сложения.png| | + | <div class="show-for-large-up">{{center|[[Файл:Правила_сложения.png|500px]]}}</div> |
<div class="hide-for-large-up">{{center|[[Файл:Правила_сложения.png|400px]]}}</div> | <div class="hide-for-large-up">{{center|[[Файл:Правила_сложения.png|400px]]}}</div> | ||
| Строка 45: | Строка 45: | ||
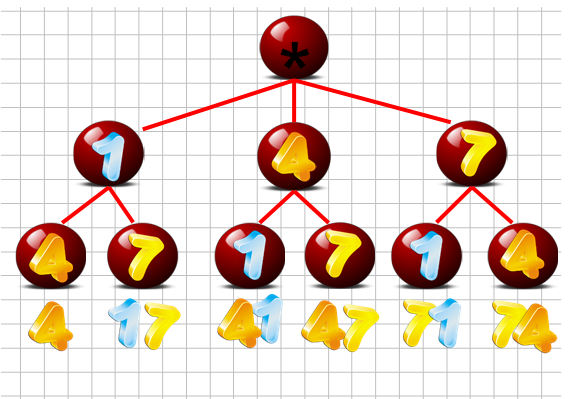
Далее от каждой цифры проводим по 2 отрезка. На концах этих отрезков записываем также цифры 1, 4, 7. Получились числа: 14, 17, 41 47, 71, 74. То есть всего получилось 6 чисел. Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола. | Далее от каждой цифры проводим по 2 отрезка. На концах этих отрезков записываем также цифры 1, 4, 7. Получились числа: 14, 17, 41 47, 71, 74. То есть всего получилось 6 чисел. Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:47.png| | + | <div class="show-for-large-up">{{center|[[Файл:47.png|500px]]}}</div> |
<div class="hide-for-large-up">{{center|[[Файл:47.png|400px]]}}</div> | <div class="hide-for-large-up">{{center|[[Файл:47.png|400px]]}}</div> | ||
| Строка 55: | Строка 55: | ||
'''Ответ:''' 6 чисел. | '''Ответ:''' 6 чисел. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Факториал.png| | + | <div class="show-for-large-up">{{center|[[Файл:Факториал.png|500px]]}}</div> |
<div class="hide-for-large-up">{{center|[[Файл:Факториал.png|400px]]}}</div> | <div class="hide-for-large-up">{{center|[[Файл:Факториал.png|400px]]}}</div> | ||
| Строка 64: | Строка 64: | ||
P8 = 8! = 40 320 | P8 = 8! = 40 320 | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Доска.png| | + | <div class="show-for-large-up">{{center|[[Файл:Доска.png|500px]]}}</div> |
<div class="hide-for-large-up">{{center|[[Файл:Доска.png|400px]]}}</div> | <div class="hide-for-large-up">{{center|[[Файл:Доска.png|400px]]}}</div> | ||
| Строка 73: | Строка 73: | ||
Решение. | Решение. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Различие между перестановками.png| | + | <div class="show-for-large-up">{{center|[[Файл:Различие между перестановками.png|500px]]}}</div> |
<div class="hide-for-large-up">{{center|[[Файл:Различие между перестановками.png|400px]]}}</div> | <div class="hide-for-large-up">{{center|[[Файл:Различие между перестановками.png|400px]]}}</div> | ||
Версия 18:18, 14 января 2018
В царице наук – математике, все эти техники объединяются в одну отрасль науки, которую называют комбинаторикой. Комбинаторика — ветвь математики, изучающая комбинации и перестановки предметов, в переводе от латинского combinare – соединять, сочетать. На протяжении двух с половиной столетий основную роль в изучении природы играл математический анализ. Положение коренным образом изменилось после создания быстродействующих вычислительных машин, компьютеров. С их помощью стало возможным делать переборы, ранее требовавшие сотен и тысяч лет. В эпоху расцвета дискретной математики изменилась и роль древнейшей области дискретной математики – комбинаторики. Комбинаторика как наука стала развиваться в VIII в. параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов.
Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицу, показывавшую, сколькими способами могут выпасть костей. Однако при этом не учитывалось, что одна и та же сумма очков может быть получена разными способами. Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных.
Известно, что для оценки вероятности победы в покере или при игре в рулетку надо просчитать, с одной стороны, общее позволяющей вычислить, сколько, например, стрит-флешей можно собрать при колоде в 52 карты. А рассчитать вероятности без комбинаторики практически невозможно. До начала расчетов необходимо навести порядок. Конечно же, мы не имеем в виду порядок на рабочем месте. Необходимо упорядочить объекты, число комбинаций с которыми мы хотим выяснить. Допустим, у нас есть банки с краской четырех цветов: красной (К), желтой (Ж), зеленой (3) и коричневой (Кор), и нам нужно разложить их по коробкам, по две разные банки в каждой. Мы можем сделать это следующим образом:
то есть шестью различными способами, так как если в одной коробке находятся банки с желтой и красной красками, то она полностью идентична той, где лежат банки с красной и желтой. Но если мы хотим парными цветами раскрасить флаги, то сделать это можно будет так: то есть двенадцатью способами, так как красно-желтый флаг не является идентичным желто-красному.
Вся наша жизнь состоит из множества разнообразных программ. Чтобы запустить ту или иную программу нужно ввести соответствующий верный пароль. В качестве кода в зависимости от рода программы могут выступать всевозможные цифры, слова или комбинации слов, поведение или действие. Комбинаторика используется в музыке, в мебельной деятельности, в различных играх (нарды, шашки, шахматы) и т.д. Читайте подробнее: http://ya-znau.ru/znaniya/zn/80, а если Вы хотите порешать задачки, то переходите сюда: http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html
Пример 1. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод? Решение: По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу сложения, можно осуществить 5+4=9 способами. Ответ: 9 способов.
Пример 2. Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза? Решение: 1 способ: перебор вариантов. Для того, чтобы не пропустить и не повторить ни одно из чисел, будем записывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4, и, наконец, с цифры 7: 14, 17, 41, 47, 71, 74. Ответ: 6 чисел.
2 способ: дерево возможных вариантов. Для этой задачи построена специальная схема. Ставим звездочку. Далее отводим от звездочки 3 отрезка. Так как в условии задачи даны 3 цифры – 1, 4, 7, то на концах отрезков ставим цифры 1, 4, 7. Далее от каждой цифры проводим по 2 отрезка. На концах этих отрезков записываем также цифры 1, 4, 7. Получились числа: 14, 17, 41 47, 71, 74. То есть всего получилось 6 чисел. Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола.
Пример 3.
Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза?
Решение:
Первую цифру двузначного числа можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать из оставшихся цифр уже двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 3∙2, т.е. 6.
Ответ: 6 чисел.
Перестановкой называется конечное множество, в котором установлен порядок элементов. Число всевозможных перестановок из n элементов вычисляется по формуле: Pn = n! Пример 4. Сколькими способами могут быть расставлены восемь участниц финального забега на восьми беговых дорожках? Решение. P8 = 8! = 40 320
Размещением из n элементов конечного множества по k, где , называют упорядоченное множество, состоящее из k элементов и вычисляется по формуле: .
Пример 5.
Из 12 учащихся нужно отобрать по одному человеку для участия в городских олимпиадах по математике, физике, истории и географии. Каждый из учащихся участвует только в одной олимпиаде. Сколькими способами это можно сделать?
Решение.
Задачи
«Волк, козел и капуста»
Крестьянину нужно перевезти через реку волка, козла и капусту. Лодка так мала, что в ней кроме крестьянина может поместиться только или волк, или козел, или капуста. Но если оставить волка с козлом, он его съест, а если оставить козла с капустой, то будет съедена капуста. Как быть крестьянину? Для решения требуется путем взаимной перестановки элементов расположить их в соответствии с условием задачи в определенном порядке. В случае с крестьянином переправу следует начать с перевозки козла. Затем крестьянин возвращается и берет волка, которого перевозит на другой берег и оставляет там, а козла возвращает назад на предыдущий берег. Оттуда забирает капусту и перевозит ее к волку. А затем возвращается и забирает козла.
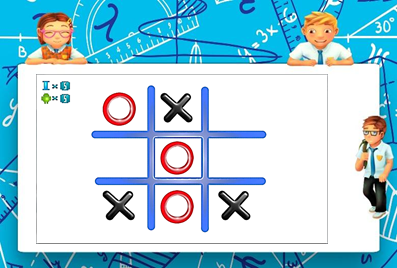
«Крестики-нолики»
Самая известная древняя игра. В квадрате, разделенном на девять клеток, игроки по очереди ставят в свободную клетку свой знак: крестик или нолик, стараясь выстроить три крестика или три нолика подряд. Тот, кто первым сделает это, тот и выигрывает. Если не делать ошибок, то игра оканчивается в ничью. Выиграть можно только в том случае, если противник ошибется. Самый правильный ход –занять угловую клетку. И если партнер не ответит на это своим знаком в центре, то он проиграл.
«Ним»
Пусть имеется одна или несколько групп предметов. Играющие берут по очереди предметы из групп по правилам, которые заранее устанавливают: какое количество предметов разрешается брать за один раз и из скольких групп. Существует множество вариантов игры, и для большинства известна наилучшая стратегия, ведущая к выигрышу.
Полезные ссылки
«Я не знаю ничего более прекрасного в арифметике, чем эти числа, называемые некоторыми планетарными, а другими – магическими», - писал о числах известный французский математик, один из создателей теории чисел Пьер де Ферма. Привлекающие естественной красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множества тайн. В своей жизни каждый из нас сталкивается с числами. Курс школьной программы, да и дальнейшую жизнь, трудно представить без них. Более подробно читаем в исследовательская работе "Магические числа" http://collegy.ucoz.ru/publ/89-1-0-3365
Глоссарий
Комбинаторика - ветвь математики, изучающая комбинации и перестановки предметов.
Библиография
- Комбинаторика. https://infourok.ru/kombinatorikaeto-interesnonauchniy-proekt-sekciya-matematika-816469.html
- Комбинаторика: основные правила и формулы. http://ya-znau.ru/znaniya/zn/80
- Савельев Л.Я. Комбинаторика и вероятность. – Новосибирск, Наука, 1975.
- Тюрин Ю.Н., Макаров А.А., Высоцкий И.Р., Ященко И.В. Теория вероятностей и статистика. – М.: МЦНМО: АО «Московские учебники», 2004.
1. Среди предметов, положенных в пирамиду, где 35 веков назад был похоронен египетский фараон Тутанхамон, нашли разграфленную доску с тремя горизонталями и фигурки для древней игры «сенет». Позже появились нарды, шашки и шахматы.
2. Первое упоминание о вопросах, близких к комбинаторным, встречаются в китайских рукописях под названием «Книга перемен».
3.Значительный толчок в развитию комбинаторики дали азартные игры, в особенности игра в кости.
4. С помощью комбинаторного метода можно прочитать забытые письменности, освоенного на наблюдениях над текстом, на сопоставлении повторяемости комбинаций.
5. Кубик Рубика – это куб, как бы разрезанный на 27 одинаковых кубиков. В исходном положении каждая грань куба окрашена в один из 6 цветов. Остроумный механизм позволяет поворачивать любой слой из 9 кубиков, примыкающий к одной грани куба, вокруг ее центра. При этом цвета граней смешиваются. Задача состоит в том, чтобы вернуть разноцветные грани кубика в исходное положение. Теоретически из любого состояния кубика можно вернуться в исходное, не более чем за 23 хода.
</p>
Лучшее время, показанное на чемпионате мира 1982 г. по скоростной сборке кубика Рубика, составило всего 22,95 секунды. А в наше время дети собирают за считанные секунды. Давайте убедимся
Математические фокусы — самые простые в исполнении. Для них не нужен реквизит, длительная подготовка и специальное место для демонстрации. Смысл таких фокусов — в отгадывании чисел, задуманных зрителями, или в каких-нибудь операциях над ними. Все чудеса основаны на математических закономерностях, такие фокусы можно проделывать на уроках математики. Смотрим и учимся математической магии. 1.
2.
3.
4.
5.
Ответы:
- Вариант
- Сочетания
- Факториал
- Событие
- Исход