Математика: Дробные числа — различия между версиями
Msu05 (обсуждение | вклад) |
Msu05 (обсуждение | вклад) |
||
| Строка 27: | Строка 27: | ||
Вся правда о дробях в видео ролике “Где применяются дроби”, посмотрев который, вы узнаете, что на самом деле дроби придумали,чтобы считать деньги. Смотрим: <div class="show-for-large-up">{{center|[[Файл:Где применяются дроби.mp4|500px]]}}</div> | Вся правда о дробях в видео ролике “Где применяются дроби”, посмотрев который, вы узнаете, что на самом деле дроби придумали,чтобы считать деньги. Смотрим: <div class="show-for-large-up">{{center|[[Файл:Где применяются дроби.mp4|500px]]}}</div> | ||
<div class="hide-for-large-up">{{center|[[Файл:Где применяются дроби.mp4|500px]]}}</div> | <div class="hide-for-large-up">{{center|[[Файл:Где применяются дроби.mp4|500px]]}}</div> | ||
| + | |||
| + | ==Математический диктант== | ||
| + | Всем известны математические диктанты. Но большинство из вас не любят такую форму контроля знаний. А зря! При систематическом написании математических диктантов вы учитесь воспринимать задания на слух, а это позволяет развивать умения слушать лекцию, речь учителя, товарищей, слушать вообще. Из различных имеющихся в нашем распоряжении каналов информации слуховой канал занимает почетное второе место после зрительного. И развивать его возможности - крайне важно. Поэтому предлагаем проверить свои силы. Бланк для выполнения задания, вопросы и ответы можно скачать и распечатать. | ||
| + | <center> | ||
| + | {| | ||
| + | |- | ||
| + | | [[Файл:Бланк_для_ответов_матнматический_диктант.jpg|450px]] | ||
| + | || [[Файл:Вопросы 1- 5 матнматический диктант.jpg|450px]] | ||
| + | |} | ||
| + | <br> | ||
| + | {| | ||
| + | |- | ||
| + | |[[Файл:Вопросы 6-10 матнматический диктант.jpg|450px]] | ||
| + | |||
| + | || [[Файл:Ответы матнматический диктант.jpg|450px]] | ||
| + | |} | ||
| + | [[Файл:New_математический_диктант_обыкновенные_дроби.mp4|450px]] | ||
| + | |||
| + | </center> | ||
==Полезные ссылки== | ==Полезные ссылки== | ||
| Строка 59: | Строка 78: | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<div class="shadow radius sbstyle" style="margin-top:20px;"> | <div class="shadow radius sbstyle" style="margin-top:20px;"> | ||
<div class="row"> | <div class="row"> | ||
Версия 16:37, 12 января 2018
Помимо натуральных чисел существуют еще дробные числа. Дробные числа, или дроби, получаются в результате деления натуральных чисел на равные части: на две, три, пять и т.д. частей. Доли используются в случаях, когда при измерении величин невозможно обойтись только целыми единицами. Например, невозможно целыми единицами (метрами) измерить рост человека.
Люди практически каждый день делят целое на части, которые называют еще долями. Чаще всего используется половина - полдня, полчаса, полкило. Но используется и деление на другое количество долей - треть, четверть, десятая, сотая. Доли образуются при делении одного предмета (буханки хлеба, листа бумаги) или единицы измерения (часа, килограмма) на равные части. Доля является каждой из равных частей единицы. Называется доля в зависимости от того, на какое количество равных частей делится единица. При делении на две части доля называется «половиной», на три - третью, на четыре - четвертью. При делении на 5, на 6, 7 частей используют названия пятая, шестая, седьмая и так далее. Также используются названия вторая, третья, четвертая доля вместо половины, трети и четверти. Например, третья, двадцатая, семьдесят третья доля записывается: 
, 
, 
, а читается одна третья, одна двадцатая, одна семьдесят третья. Если единицу разделили на n равных частей, то записывается дробь 
и читается одна энная.
В первых учебниках математики (VII в.) дроби называли долями, позднее «ломаными числами». В русском языке слово дробь появилось в VIII веке, оно происходит от глагола «дробить» — разбивать, ломать на части. Числа, которые являются долями или их суммами, называют дробными числами. Для дробных чисел используется и название дроби. В старых руководствах есть следующие названия дробей на Руси: половина, треть, четь, полтреть, полчеть, полполтреть, полполчеть, полполполтреть (малая треть). Предлагаем посмотреть видео сюжет и узнать, какие названия дробей дошли до наших дней.
Для записи дробей используется дробная черта и два натуральные числа. Под дробной чертой записывается знаменатель дроби, который показывает, из каких долей состоит дробь. Над чертой записывается числитель дроби, который показывает, из суммы скольких долей состоит дробь. Чаще всего используется десятичная нумерация. Название нумерации произошло от следующего правила: единица каждого разряда в 10 раз больше единицы предыдущего разряда. Разряд единиц является самым младшим в записи натуральных чисел. Единица предыдущего младшего разряда должна быть в 10 раз меньше единицы каждого разряда. Разряд десятых долей размещается правее разряда единиц и отделяется от разряда единиц запятой.
можно записать так: 13,4, а число 
запишется 2,8.Разряды справа от запятой могут продолжаться и для них действует правило: каждая единица разряда в 10 раз меньше единицы предыдущего разряда. 1-й разряд после запятой называется десятыми долями, 2-й разряд после запятой -- сотыми доли, 3-й разряд после запятой - тысячными долями. Записанная с помощью цифр и запятой дробь называется десятичной дробью, а записанная с помощью дробной черты дробь называется обыкновенной дробью.
Для записи обыкновенной дроби в виде десятичной нужно числитель разделить на знаменатель.
О дробях
Вся правда о дробях в видео ролике “Где применяются дроби”, посмотрев который, вы узнаете, что на самом деле дроби придумали,чтобы считать деньги. Смотрим:Математический диктант
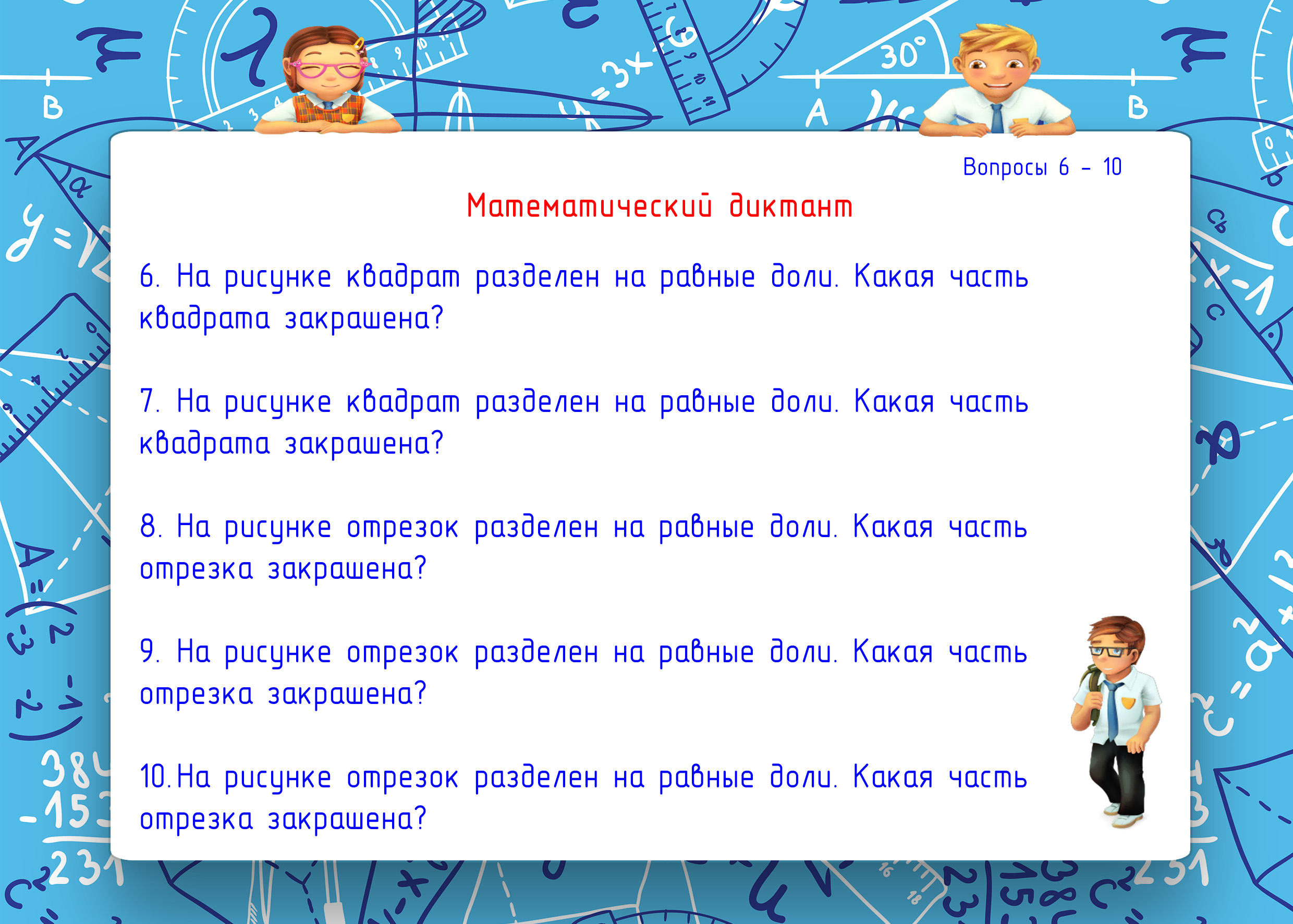
Всем известны математические диктанты. Но большинство из вас не любят такую форму контроля знаний. А зря! При систематическом написании математических диктантов вы учитесь воспринимать задания на слух, а это позволяет развивать умения слушать лекцию, речь учителя, товарищей, слушать вообще. Из различных имеющихся в нашем распоряжении каналов информации слуховой канал занимает почетное второе место после зрительного. И развивать его возможности - крайне важно. Поэтому предлагаем проверить свои силы. Бланк для выполнения задания, вопросы и ответы можно скачать и распечатать.
|
|
|
|
Полезные ссылки
1. История дробей насчитывает не одно тысячелетие. Умение делить целое на части возникло на территории древнего Египта и Вавилона. С годами усложнялись операции, проделываемые с дробями, менялась форма их записи. У каждого государства древнего мира были свои особенности во «взаимоотношениях» с этим разделом математики - Читайте подробнее на: http://fb.ru/article/236507/drobi-istoriya-drobey-istoriya-vozniknoveniya-obyiknovennyih-drobey
2. К десятичным дробям математики пришли в разное время в Азии и Европе. Зарождение и развитие десятичных дробей в некоторых странах Азии было тесно связано с метрологией (наукой о мерах). Уже во II веке до нашей эры там существовала десятичная система мер длины. Интересно? Тогда подробности здесь: http://matemdp84.blogspot.ru/2013/02/blog-post_8.html
Глоссарий
Натуральные числа – числа, которые используют при счёте предметов
Библиография
- Дробные числа.: [Электронный ресурс] // Avtor24, 2017 URL: https://author24.ru/spravochniki/matematika/drobnye_chisla/ (дата обращения: 20. 11. 2017)
- Дроби: история дробей. История возникновения обыкновенных дробей.: [Электронный ресурс] // «ФБ», 2017 URL: http://fb.ru/article/236507/drobi-istoriya-drobey-istoriya-vozniknoveniya-obyiknovennyih-drobey (дата обращения: 20. 11. 2017)
- Название частых дробей. Видео «Где применяются дроби».: [Электронный ресурс] // Zero to Hero YouTube, 2017. URL: https://www.youtube.com/watch?v=y75kaLTzSKo (дата обращения: 20. 11. 2017)
- Интересная математика. Десятичные дроби. URL: [Электронный ресурс] // Google 1999 – 2017 URL:http://matemdp84.blogspot.ru/2013/02/blog-post_8.html (дата обращения: 20. 11. 2017)
овременная система записи дробей с числителем и знаменателем создана в Индии. Индийцы использовали обыкновенные дроби. Обозначение обыкновенных дробей с помощью числителя и знаменателя принято в Индии еще в VIII веке до н.э., но без дробной черты. Различие было в том, что знаменатель записывался сверху, а числитель -- снизу. Современная запись дробей стала использоваться уже арабами. В Вавилоне использовали шестидесятеричные дроби. Знаменателями дробей были числа 60, 602, 603 и т.д. Но не все можно было точно выразить через шестидесятеричные. Например, дробь одну седьмую можно было выразить только приближенно. Шестидесятеричные дроби использовали греческие и арабские математики и астрономы. Но с натуральными числами, которые записывались в десятичной и шестидесятеричной систем было неудобно работать, тем более сложно было работать с обыкновенными дробями. Тогда голландский математик Симон Стевин предложил перейти к десятичным дробям. Сначала их запись была очень сложной, но впоследствии стала использоваться современная запись. Сегодня в компьютерной технике используются двоичные дроби, которые ранее применялись на Руси: половина, четь, полчети, пол-полчети.
При изучении обыкновенных дробей трудно запомнить, какая дробь правильная, а какая - нет, какое место занимают числитель и знаменатель.
Чтобы не путать расположение числителя и знаменателя дроби, воспользуйтесь таким предложением "Человек стоит на земле" и соответствующим рисунком. Слово "человек" начинается на букву "ч" и слово "числитель" тоже начинается на букву "ч".
Слово "земля" начинается на букву "з" и слово "знаменатель" тоже начинается на букву "з".
Значит, числитель и знаменатель дроби будут расположены по отношению друг к другу точно так, как человек и земля, изображённые на рисунке.
Человек сверху, земля снизу и, соответственно, числитель сверху, знаменатель снизу.
Определение правильной дроби звучит следующим образом: это такая дробь, числитель которой меньше знаменателя. На схематическом изображении правильной дроби видно, что над чертой стоит кубик меньшего размера, чем под ней. А в случае неправильной дроби - наоборот. Для дроби, равной единице, кубики одинакового размера.
Попробуйте ответить правильно на пять вопросов: