Математика: Чыныгы сандар — различия между версиями
Msu05 (обсуждение | вклад) |
Msu05 (обсуждение | вклад) (→Сандардын тарыхы) |
||
| Строка 8: | Строка 8: | ||
<div class="hide-for-large-up">{{center|[[Файл:Числа_вокруг_нас_кт.gif|400px]]}}</div> | <div class="hide-for-large-up">{{center|[[Файл:Числа_вокруг_нас_кт.gif|400px]]}}</div> | ||
| − | + | Азыркы жашообузду сандарсыз элестетүү кыйын. Алар бизди бардык тарабыбыздан курчап турат. Биз аларды күн сайын кездештиребиз жана ар кандай техникалык ыкмалардын жардамы менен аларга ондогон, жүздөгөн жана миңдеген амалдарды жасайбыз. Биз буга абдан көнгөндүктөн сандардын тарыхы бизди кызыктырбайт дагы, а көптөрү бул жөнүндө жөн гана ойлошпойт дагы. Бирок өткөндү билмейинче азыркыны түшүнүүгө болбойт, ошондуктан башатты түшүнүүгө аракет кылуу керек. Анда сандардын өнүгүү тарыхы кандай? Алар качан пайда болушкан, адамдар аларды түзүүгө кандайча жетишкен? Келгиле анда бул жөнүндө билели! | |
<div class="show-for-large-up">{{center|[[Файл:Сандар тарыхы.jpg|500px]]}}</div> | <div class="show-for-large-up">{{center|[[Файл:Сандар тарыхы.jpg|500px]]}}</div> | ||
| Строка 20: | Строка 20: | ||
Абал биздин кылымга чейинки биринчи кылымдарда өзгөрө баштаган. Диофант Александрийский мурунку салттарга каршы бөлчөктөрдү дагы натуралдык сан катары караган, а өзүнүн “Арифметика” китебинин IV-сүндө бир жыйынтык жөнүндө жазган: “Сан рационалдык эмес экен”. Античный илимдин кыйрашынан кийин алдыңкы планга индиялык жана исламдык математика чыккан, алар үчүн ченөөнүн жана эсептөөнүн каалагандай жыйынтыгы сан болуп саналган. Бул көз караштар акырындап орто кылымдагы Европаны дагы өйдө болгон, ал жакта алгач рационалдык жана иррационалдык (акылсыз дегендей) сандар (аларды жалган, маанисиз, керең ж.б. дагы аташкан). Иррационалдык сандардын укугундагы толук теңдемелер Симон Стевиндин (XVI кылымдын аягы) эмгектери менен байланыштуу. Андан жүз жыл өткөндөн кийин Ньютон өзүнүн “Универсалдык арифметика” (1707) сында классикалык аныктаманы берген (чыныгы) сандар бирдик эталонун ченөөдө жыйынтыгынын катышы. | Абал биздин кылымга чейинки биринчи кылымдарда өзгөрө баштаган. Диофант Александрийский мурунку салттарга каршы бөлчөктөрдү дагы натуралдык сан катары караган, а өзүнүн “Арифметика” китебинин IV-сүндө бир жыйынтык жөнүндө жазган: “Сан рационалдык эмес экен”. Античный илимдин кыйрашынан кийин алдыңкы планга индиялык жана исламдык математика чыккан, алар үчүн ченөөнүн жана эсептөөнүн каалагандай жыйынтыгы сан болуп саналган. Бул көз караштар акырындап орто кылымдагы Европаны дагы өйдө болгон, ал жакта алгач рационалдык жана иррационалдык (акылсыз дегендей) сандар (аларды жалган, маанисиз, керең ж.б. дагы аташкан). Иррационалдык сандардын укугундагы толук теңдемелер Симон Стевиндин (XVI кылымдын аягы) эмгектери менен байланыштуу. Андан жүз жыл өткөндөн кийин Ньютон өзүнүн “Универсалдык арифметика” (1707) сында классикалык аныктаманы берген (чыныгы) сандар бирдик эталонун ченөөдө жыйынтыгынын катышы. | ||
| − | + | Сандардын өнүгүүсү жөнүндөгү түшүнүктүн тарыхын схема түрүндө көрсөтүүгө болот: | |
<div class="show-for-large-up">{{center|[[File:Сан_пазл.png|500px]]}}</div> | <div class="show-for-large-up">{{center|[[File:Сан_пазл.png|500px]]}}</div> | ||
Версия 06:11, 20 мая 2018
Сандардын тарыхы
Азыркы жашообузду сандарсыз элестетүү кыйын. Алар бизди бардык тарабыбыздан курчап турат. Биз аларды күн сайын кездештиребиз жана ар кандай техникалык ыкмалардын жардамы менен аларга ондогон, жүздөгөн жана миңдеген амалдарды жасайбыз. Биз буга абдан көнгөндүктөн сандардын тарыхы бизди кызыктырбайт дагы, а көптөрү бул жөнүндө жөн гана ойлошпойт дагы. Бирок өткөндү билмейинче азыркыны түшүнүүгө болбойт, ошондуктан башатты түшүнүүгө аракет кылуу керек. Анда сандардын өнүгүү тарыхы кандай? Алар качан пайда болушкан, адамдар аларды түзүүгө кандайча жетишкен? Келгиле анда бул жөнүндө билели!
Биринчи өнүккөн сандык система, Байыркы Грецияда курулган, өзүнө натуралдык гана сандарды жана алардын катышын камтыган (пропорция, азыркы түшүнүктө- рационалдык сандар). Бирок геометриянын жана астрономиянын максаттары үчүн бул жетишсиз экени бат эле белгилүү болгон, мисалы: квадраттын диагоналынын анын жактарынын узундугна катышы натуралдык да рационалдык да боло албасы көрсөтүлгөн. Бул абалдан чыгуу үчүн Евдокс Книдский сандарга кошумча киргизүүнү киргизген, геометриялык чоңдук кеңири түшүнүгү, башкача айтканда кесиндинин узундугу, аянты жана көлөмү, Евдокстун теориясы- бул чыныгы сандардын геометриялык модели.
Абал биздин кылымга чейинки биринчи кылымдарда өзгөрө баштаган. Диофант Александрийский мурунку салттарга каршы бөлчөктөрдү дагы натуралдык сан катары караган, а өзүнүн “Арифметика” китебинин IV-сүндө бир жыйынтык жөнүндө жазган: “Сан рационалдык эмес экен”. Античный илимдин кыйрашынан кийин алдыңкы планга индиялык жана исламдык математика чыккан, алар үчүн ченөөнүн жана эсептөөнүн каалагандай жыйынтыгы сан болуп саналган. Бул көз караштар акырындап орто кылымдагы Европаны дагы өйдө болгон, ал жакта алгач рационалдык жана иррационалдык (акылсыз дегендей) сандар (аларды жалган, маанисиз, керең ж.б. дагы аташкан). Иррационалдык сандардын укугундагы толук теңдемелер Симон Стевиндин (XVI кылымдын аягы) эмгектери менен байланыштуу. Андан жүз жыл өткөндөн кийин Ньютон өзүнүн “Универсалдык арифметика” (1707) сында классикалык аныктаманы берген (чыныгы) сандар бирдик эталонун ченөөдө жыйынтыгынын катышы.
Сандардын өнүгүүсү жөнүндөгү түшүнүктүн тарыхын схема түрүндө көрсөтүүгө болот:
Понятие вещественного числа
Чыныгы, же болбосо анык сандар – математикалык абстракция, курчап турган дүйнөдөгү геометриялык жана физикалык ченөөлөрдүн зарылдыгынан келип чыккан, ошондой эле, тамырдан чыгаруу, логарифмаларды чыгаруу, алгебралык теңдемелерди эсептөө сыяктуу амалдарды аткаруу.
Көбүнчө чыныгы сандарды R менен белгилешет (“жарым кара R”) (англ. blackboardbold «R») латынчадан realis –анык жана чыныгы же сандык түз сызык деп да атай беришет. Официалдуу чыныгы сандар жөнөкөй объектилердин негизинде түзүлөт.
Свойства арифметических действий над вещественными числами. Основные законы алгебры.
Над действительными числами можно выполнять арифметические действия. Они удовлетворяют тем же свойствам, что и действия над рациональными числами.
- a+b=b+a.
- (a+b)+c=a+(b+c).
- a+0=a .
- a+(-a)=0.
- a∙b=b∙a.
- (a∙b)∙c=a∙(b∙c).
- a∙(b+c)=a∙b+a∙c.
- a∙1=a.
- a∙
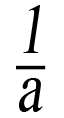 =1,a≠0.
=1,a≠0.
Эти свойства называют основными законами алгебры.
Свойства 1 и 5 выражают переместительный закон сложения и умножения соответственно;
Cвойства 2 и 6 выражают сочетательный закон;
Cвойство 7 — распределительный закон умножения относительно сложения;
Cвойства 3 и 8 указывают на наличие нейтрального элемента для сложения и умножения соответственно;
Cвойства 4 и 10 – на наличие нейтрализующего элемента соответственно.
Из этих свойств выделяются другие свойства. Например, a∙0=0. В самом деле, имеем:
a∙0=a∙(b+(-b))= a∙b+a∙(-b)= a∙b+(-a∙b)=0
Пайдалуу шилтемелер
- Видеоурок на тему «Вещественные числа»: [Электронный ресурс] //Образование. Обучение - Znaika TV. Знайка.ру YouTube, 2018 https://www.youtube.com/watch?v=WrIXyM_rv-Y (Дата посещения: 14.04.2018)
- Видеоурок на тему «Модуль действительного числа и его свойства» поможет сформировать понятие модуля.: [Электронный ресурс] // Люди и блоги YouTube, 2018 URL: https://www.youtube.com/watch?v=KbtNg7n9GpU (Дата посещения: 14.04.2018)
- В книге Сергея Боброва «Волшебный двурог, или Правдивая история небывалых приключений нашего отважного друга Ильи Алексеевича Камова в неведомой стране» в занимательной форме рассказывается немало интересного для тех, кто любит точные науки и математику. Здесь вы узнаете о развитии математики, о ее значении в технике, а особенно об одной из важнейших отраслей математики - так называемом математическом анализе. На доступных примерах познакомитесь с элементами дифференциального и интегрального исчислений. Книгу можно использовать для самостоятельного изучения математики старшеклассникам школы или маленьким вундеркиндам.: [Электронный ресурс] // ЛитЛайф - литературный клуб URL: https://litlife.club/br/?b=282385 (Дата посещения: 14.04.2018)
Мисалдар
Глоссарий
- Оң сандар- сан, нолдон чоң.
- Терс сандар- минус (−) белгиси менен сандар, мисалы: −1, −2, −3 ж.б. минус бир, минус эки, минус үч ж.б. болуп окулат.
- Бүтүн сандар – бул натуралдык сандар, нол саны, ошондой эле натуралдык сандарга карама каршы сандар.
- Натуралдык сандар - бул сандар, предметтерди саноо үчүн же бирдей предметтер арасындагы тигил же бул предметтин катар номерин көрсөтүү үчүн колдонулат.
- Рационалдык сандар - Бул сандарды кадимки бөлчөк, терс кадимки бөлчөк жана нол саны түрүндө жазууга болот.
- Иррационалдык сандар - санда, ондук жазууда чексиз, мезгилсиз ондук бөлчөктөрдү көрсөтөт.
Модуль вещественного числа - Модуль вещественного числа а - это само число а, если а≥0, и противоположное число а , если а<0 .
Библиография
1. Гордый Рим трубил победу… Сергей Бобров.: [Электронный ресурс] // Antipodes Association Incorporated URL: http://www.antipodes.org.au/pr_pi_60.html (Дата посещения: 14.04.2018)
2. Совершенный Письмовник.: [Электронный ресурс] // Antipodes Association Incorporated URL: http://www.antipodes.org.au/pr_pi_all.html#Collection (Дата посещения: 14.04.2018)
3. Карл Эдуард Саган Контакт https: [Электронный ресурс] // ЛитЛайф - литературный клуб URL: https://litlife.club/br/?b=260441 (Дата посещения: 17.04.2018)
4. Сергей Бобров «Волшебный двурог, или Правдивая история небывалых приключений нашего отважного друга Ильи Алексеевича Камова в неведомой стране»: [Электронный ресурс] // ЛитЛайф - литературный клуб URL: https://litlife.club/br/?b=282385 (Дата посещения: 14.04.2018)
5. Факты о числе Пи.: [Электронный ресурс] // Удивительные факты для всех! 2013-2018 URL:http://amazing-facts.ru/science/fakty_o_chisle_pi.html (Дата посещения: 17.04.2018)
6. 10 удивительных визуализаций числа Пи: [Электронный ресурс] // DataReview.info URL: http://datareview.info/article/10-udivitelnyih-vizualizatsiy-chisla-pi/ (Дата посещения: 17.04.2018) 10 удивительных фактов о числе Пи: [Электронный ресурс] // 2013–2018 Пабли URL: http://www.publy.ru/post/25177 (Дата посещения: 17.04.2018)
7. Видеоурок на тему «Модуль действительного числа и его свойства»: [Электронный ресурс] // Люди и блоги YouTube, 2018 URL:https://www.youtube.com/watch?v=KbtNg7n9GpU (Дата посещения: 14.04.2018)
8. Видеоурок на тему «Вещественные числа» : [Электронный ресурс] //Образование. Обучение - Znaika TV. Знайка.ру YouTube, 2018 https://www.youtube.com/watch?v=WrIXyM_rv-Y (Дата посещения: 14.04.2018)
9. Евдокс Книдский : Материал из Википедии — свободной энциклопедии : Версия 91658954, сохранённая в 16:03 UTC 22 марта 2018 // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2018. — Режим доступа: http://ru.wikipedia.org/?oldid=91658954 (Дата посещения: 17.04.2018)
10. М. Я. Выгодский. Справочник по элементарной математике. Москва 1986.
1. Алгач араб сандары түз кесиндилерден гана турган, нолдон бөлөгү, “сандардын мааниси алардын жазылышындагы бурчтарына дал келет” принциби боюнча түзүлгөн. Мисалы: нол-бурчу жок, бир-бир бурч, эки-эки бурч ж.б
2. Брахмагупта- индиялык математик, VII кылымда жашаган, биринчилерден болуп оң жана терс сандарды пайдаланган
3. Американын Индиана штатында: штаттын аймагында π санын 4 кө барабар деп эсептөө закону бар.
4. Илимий коомдун көп өкүлдөрү π математикалык константа деп аташат, ал өзүнүн сырлары жана жашыруун маанилери бар сан. Эгерде бир нече изилдөөлөрдү карап көрсөк, бардык кылымдагы жана элдердеги окумуштуулар бул санга көп көңүл бөлүшкөн, ошондуктан биз оңой эле π жөнүндө эң кызыктуу фактыларды таба алдык.
Дэвид Макдональд переложил число π на ноты с точностью до 122 знака после запятой. Механизм очень прост: каждой музыкальной ступени гаммы была присвоена цифра от 0 до 9. За основу была взята тональность ля-минор. И вот, число Пи превратилось в удивительно гармоничную и даже несколько «космическую» мелодию, исполнение которой сопровождается интересными фактами о числе π.
В научно-фантастическом романе «Контакт» американского астрофизика Карла Сагана учеными предпринимается попытка записать в двоичной системе число Пи. Так они приходят к выводу о существовании внеземного разума.
В 1998 году художественный фильм «Пи: Вера в хаос» режиссера Даррена Аронофски получил премию за лучшую режиссуру драматического фильма на кинофестивале Сандэнс. По сюжету, главный герой ищет простые ответы на вопросы, связанные с числом Пи, что сводит его с ума.
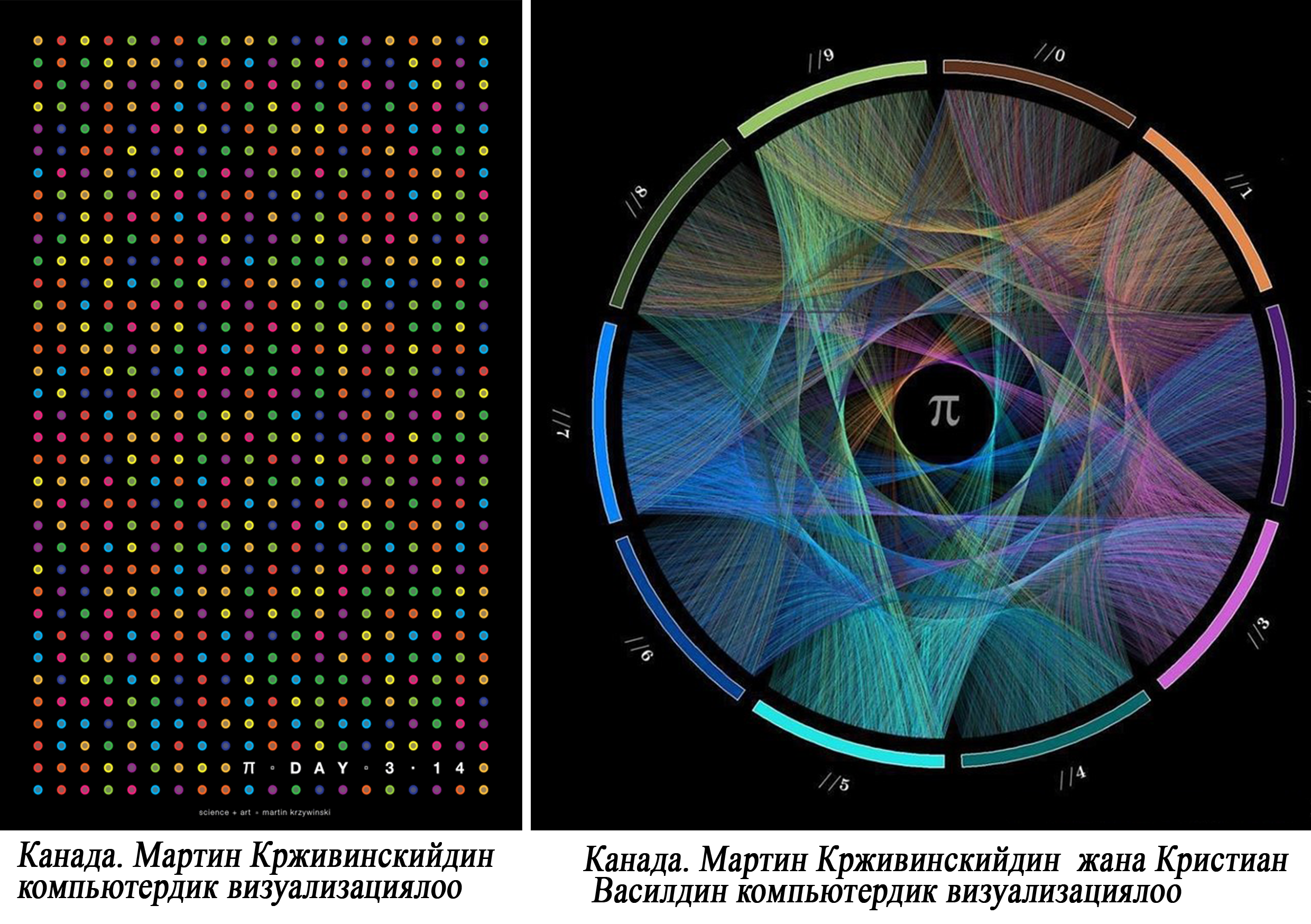
Взглянув на то, как можно изобразить число π, понимаешь, насколько красива математика.
Этот вопрос терзает людей не одно столетие. Что только они не придумывали для его запоминания. Стихотворение про число π поможет сделать это быстрее.
Гордый Рим трубил победу
Над твердыней Сиракуз;
Но трудами Архимеда
Много больше я горжусь.
Надо нынче нам заняться,
Оказать старинке честь,
Чтобы нам не ошибаться,
Чтоб окружность верно счесть,
Надо только постараться
И запомнить все как есть
Три — четырнадцать —
пятнадцать — девяносто два и шесть!
Сергей Бобров