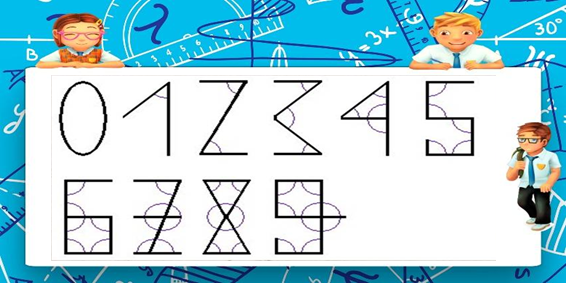Математика: Чыныгы сандар — различия между версиями
Msu05 (обсуждение | вклад) (Новая страница: «__NOTOC__ <div class="row mat-bg"> <div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> {{Якорь|Начало}} <div clas…») |
Msu05 (обсуждение | вклад) |
||
| Строка 8: | Строка 8: | ||
| − | + | Биринчи өнүккөн сандык система, Байыркы Грецияда курулган, өзүнө натуралдык гана сандарды жана алардын катышын камтыган (пропорция, азыркы түшүнүктө- рационалдык сандар). Бирок геометриянын жана астрономиянын максаттары үчүн бул жетишсиз экени бат эле белгилүү болгон, мисалы: квадраттын диагоналынын анын жактарынын узундугна катышы натуралдык да рационалдык да боло албасы көрсөтүлгөн. Бул абалдан чыгуу үчүн Евдокс Книдский сандарга кошумча киргизүүнү киргизген, геометриялык чоңдук кеңири түшүнүгү, башкача айтканда кесиндинин узундугу, аянты жана көлөмү, Евдокстун теориясы- бул чыныгы сандардын геометриялык модели. | |
| − | + | Абал биздин кылымга чейинки биринчи кылымдарда өзгөрө баштаган. Диофант Александрийский мурунку салттарга каршы бөлчөктөрдү дагы натуралдык сан катары караган, а өзүнүн “Арифметика” китебинин IV-сүндө бир жыйынтык жөнүндө жазган: “Сан рационалдык эмес экен”. Античный илимдин кыйрашынан кийин алдыңкы планга индиялык жана исламдык математика чыккан, алар үчүн ченөөнүн жана эсептөөнүн каалагандай жыйынтыгы сан болуп саналган. Бул көз караштар акырындап орто кылымдагы Европаны дагы өйдө болгон, ал жакта алгач рационалдык жана иррационалдык (акылсыз дегендей) сандар (аларды жалган, маанисиз, керең ж.б. дагы аташкан). Иррационалдык сандардын укугундагы толук теңдемелер Симон Стевиндин (XVI кылымдын аягы) эмгектери менен байланыштуу. Андан жүз жыл өткөндөн кийин Ньютон өзүнүн “Универсалдык арифметика” (1707) сында классикалык аныктаманы берген (чыныгы) сандар бирдик эталонун ченөөдө жыйынтыгынын катышы. | |
| − | ''' | + | '''Чыныгы''', же '''болбосо анык сандар''' – математикалык абстракция, курчап турган дүйнөдөгү геометриялык жана физикалык ченөөлөрдүн зарылдыгынан келип чыккан, ошондой эле, тамырдан чыгаруу, логарифмаларды чыгаруу, алгебралык теңдемелерди эсептөө сыяктуу амалдарды аткаруу. Бул сандарды 2 чоңдуктун бирдей көлөмдөгү катыштары катары эсептөө, же түз сызыктагы чекиттин абалында жазуу. |
<div class="show-for-large-up">{{center|[[File:Вещественное_число.png|500px]]}}</div> | <div class="show-for-large-up">{{center|[[File:Вещественное_число.png|500px]]}}</div> | ||
<div class="hide-for-large-up">{{center|[[File:Вещественное_число.png|500px]]}}</div> | <div class="hide-for-large-up">{{center|[[File:Вещественное_число.png|500px]]}}</div> | ||
| − | + | Көбүнчө чыныгы сандарды R менен белгилешет (“жарым кара R”) (англ. blackboardbold «R») латынчадан realis –анык жана чыныгы же сандык түз сызык деп да атай беришет. Официалдуу чыныгы сандар жөнөкөй объектилердин негизинде түзүлөт. | |
<div class="show-for-large-up">{{center|[[File:1,2,0,1.png|500px]]}}</div> | <div class="show-for-large-up">{{center|[[File:1,2,0,1.png|500px]]}}</div> | ||
| Строка 26: | Строка 26: | ||
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | ||
| − | == | + | ==Пайдалуу шилтемелер== |
| − | + | Адамдар таааныш болгон тарыхтагы биринчи сандар натуралдык сандар болгон: 1,2,3 ж.б. Мындай сандардын жардамы менен кандайдыр бир бүтүн предметтин санын эсептөөгө болот, бирок, натуралдык сандар чоң жетишпегендикке ээ болушкан. Мына бул чыныгы сандар чындыгында, чексиз сандары бир натуралдык сандарга карганда көп. Натуралдык сандардын жардамы менен бардык чыныгы сандарды санап бүткөнгө ыкма ойлоп тапканга мүмкүн эмес. Кененирээк: http://wreferat.baza-referat.ru/ Чыныгы сандар | |
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | ||
| − | == | + | ==Табышмактар== |
<div class="show-for-large-up">{{center|[[File:Загадки.jpg|500px]]}}</div> | <div class="show-for-large-up">{{center|[[File:Загадки.jpg|500px]]}}</div> | ||
<div class="hide-for-large-up">{{center|[[File:Загадки.jpg|500px]]}}</div> | <div class="hide-for-large-up">{{center|[[File:Загадки.jpg|500px]]}}</div> | ||
| Строка 37: | Строка 37: | ||
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | ||
==Глоссарий== | ==Глоссарий== | ||
| − | *''' | + | *'''Оң сандар''' - сан, нолдон чоң. |
| − | *''' | + | *'''Терс сандар'''- минус (−) белгиси менен сандар, мисалы: −1, −2, −3 ж.б. минус бир, минус эки, минус үч ж.б. болуп окулат. |
| − | *''' | + | *'''Бүтүн сандар''' – бул натуралдык сандар, нол саны, ошондой эле натуралдык сандарга карама каршы сандар. |
| − | *''' | + | *'''Натуралдык сандар''' - бул сандар, предметтерди саноо үчүн же бирдей предметтер арасындагы тигил же бул предметтин катар номерин көрсөтүү үчүн колдонулат. |
| − | *''' | + | *'''Рационалдык сандар''' - Бул сандарды кадимки бөлчөк, терс кадимки бөлчөк жана нол саны түрүндө жазууга болот. |
| − | *''' | + | *'''Иррационалдык сандар''' - санда, ондук жазууда чексиз, мезгилсиз ондук бөлчөктөрдү көрсөтөт. |
| − | *'''Мантисса'''- | + | *'''Мантисса''' - сандын бүтүн бөлүгү. |
| + | |||
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | ||
| Строка 67: | Строка 68: | ||
</div> | </div> | ||
| − | 1. | + | 1. Алгач араб сандары түз кесиндилерден гана турган, нолдон бөлөгү, “сандардын мааниси алардын жазылышындагы бурчтарына дал келет” принциби боюнча түзүлгөн. Мисалы: нол-бурчу жок, бир-бир бурч, эки-эки бурч ж.б |
{{center|[[Файл:0 1 2.png|400px]]}} | {{center|[[Файл:0 1 2.png|400px]]}} | ||
| − | 2. Брахмагупта- | + | 2. Брахмагупта- индиялык математик, VII кылымда жашаган, биринчилерден болуп оң жана терс сандарды пайдаланган |
{{center|[[Файл:Брахмагупта 1.png|400px]]}} | {{center|[[Файл:Брахмагупта 1.png|400px]]}} | ||
| − | 3. | + | 3. Американын Индиана штатында: штаттын аймагында р санын 4 кө барабар деп эсептөө закону бар. |
| − | + | 4. Социализмдин өнүккөн маалында азыктардын баасы алардын белгилерине жараша колдонулган. Эң белгилүү газдуу суусундуктар (Coca-Cola, Fanta, Sprite) 1 с. 49 тый. (0,5л) жана 2с.87 тый. (1л) тураарын ар бир бала билген. Күтүлбөгөн таң калаарлык ачылыш бул биринчи сан экинчинин даражасынан курулган π санын берет. Эскертем, “пи” саны фундаменталдык костанта болуп саналат, “жашоонун константасы” деп айтса да болот. | |
| − | + | 5. Илимий коомдун көп өкүлдөрү π математикалык константа деп аташат, ал өзүнүн сырлары жана жашыруун маанилери бар сан. Эгерде бир нече изилдөөлөрдү карап көрсөк, бардык кылымдагы жана элдердеги окумуштуулар бул санга көп көңүл бөлүшкөн, ошондуктан биз оңой эле Piсаны жөнүндө эң кызыктуу фактыларды таба алдык жана алардын текс формасы менен видео презентацияларын көрсөтөбүз | |
| − | |||
{{center|[[Файл:7_фактов_о_числе_Пи_–_интересные_особенности_и_математические_исследования.mp4|400px]]}} | {{center|[[Файл:7_фактов_о_числе_Пи_–_интересные_особенности_и_математические_исследования.mp4|400px]]}} | ||
| Строка 89: | Строка 89: | ||
<div class="shadow radius sbstyle" style="margin-top:20px;"> | <div class="shadow radius sbstyle" style="margin-top:20px;"> | ||
<div class="row"> | <div class="row"> | ||
| − | <div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;"> | + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Пи санын кантип жаттап калуу керек</div> |
</div> | </div> | ||
| − | + | Пи саны үчүн көптөгөн обондор жана ырлар жазылган. | |
{{center|[[Файл:Музыка_числа_Пи.mp4|400px]]}} | {{center|[[Файл:Музыка_числа_Пи.mp4|400px]]}} | ||
Версия 15:34, 16 апреля 2018
Биринчи өнүккөн сандык система, Байыркы Грецияда курулган, өзүнө натуралдык гана сандарды жана алардын катышын камтыган (пропорция, азыркы түшүнүктө- рационалдык сандар). Бирок геометриянын жана астрономиянын максаттары үчүн бул жетишсиз экени бат эле белгилүү болгон, мисалы: квадраттын диагоналынын анын жактарынын узундугна катышы натуралдык да рационалдык да боло албасы көрсөтүлгөн. Бул абалдан чыгуу үчүн Евдокс Книдский сандарга кошумча киргизүүнү киргизген, геометриялык чоңдук кеңири түшүнүгү, башкача айтканда кесиндинин узундугу, аянты жана көлөмү, Евдокстун теориясы- бул чыныгы сандардын геометриялык модели.
Абал биздин кылымга чейинки биринчи кылымдарда өзгөрө баштаган. Диофант Александрийский мурунку салттарга каршы бөлчөктөрдү дагы натуралдык сан катары караган, а өзүнүн “Арифметика” китебинин IV-сүндө бир жыйынтык жөнүндө жазган: “Сан рационалдык эмес экен”. Античный илимдин кыйрашынан кийин алдыңкы планга индиялык жана исламдык математика чыккан, алар үчүн ченөөнүн жана эсептөөнүн каалагандай жыйынтыгы сан болуп саналган. Бул көз караштар акырындап орто кылымдагы Европаны дагы өйдө болгон, ал жакта алгач рационалдык жана иррационалдык (акылсыз дегендей) сандар (аларды жалган, маанисиз, керең ж.б. дагы аташкан). Иррационалдык сандардын укугундагы толук теңдемелер Симон Стевиндин (XVI кылымдын аягы) эмгектери менен байланыштуу. Андан жүз жыл өткөндөн кийин Ньютон өзүнүн “Универсалдык арифметика” (1707) сында классикалык аныктаманы берген (чыныгы) сандар бирдик эталонун ченөөдө жыйынтыгынын катышы.
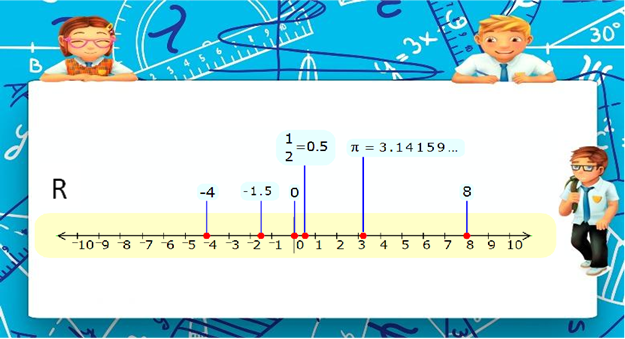
Чыныгы, же болбосо анык сандар – математикалык абстракция, курчап турган дүйнөдөгү геометриялык жана физикалык ченөөлөрдүн зарылдыгынан келип чыккан, ошондой эле, тамырдан чыгаруу, логарифмаларды чыгаруу, алгебралык теңдемелерди эсептөө сыяктуу амалдарды аткаруу. Бул сандарды 2 чоңдуктун бирдей көлөмдөгү катыштары катары эсептөө, же түз сызыктагы чекиттин абалында жазуу.
Көбүнчө чыныгы сандарды R менен белгилешет (“жарым кара R”) (англ. blackboardbold «R») латынчадан realis –анык жана чыныгы же сандык түз сызык деп да атай беришет. Официалдуу чыныгы сандар жөнөкөй объектилердин негизинде түзүлөт.
Пайдалуу шилтемелер
Адамдар таааныш болгон тарыхтагы биринчи сандар натуралдык сандар болгон: 1,2,3 ж.б. Мындай сандардын жардамы менен кандайдыр бир бүтүн предметтин санын эсептөөгө болот, бирок, натуралдык сандар чоң жетишпегендикке ээ болушкан. Мына бул чыныгы сандар чындыгында, чексиз сандары бир натуралдык сандарга карганда көп. Натуралдык сандардын жардамы менен бардык чыныгы сандарды санап бүткөнгө ыкма ойлоп тапканга мүмкүн эмес. Кененирээк: http://wreferat.baza-referat.ru/ Чыныгы сандар
Табышмактар
Глоссарий
- Оң сандар - сан, нолдон чоң.
- Терс сандар- минус (−) белгиси менен сандар, мисалы: −1, −2, −3 ж.б. минус бир, минус эки, минус үч ж.б. болуп окулат.
- Бүтүн сандар – бул натуралдык сандар, нол саны, ошондой эле натуралдык сандарга карама каршы сандар.
- Натуралдык сандар - бул сандар, предметтерди саноо үчүн же бирдей предметтер арасындагы тигил же бул предметтин катар номерин көрсөтүү үчүн колдонулат.
- Рационалдык сандар - Бул сандарды кадимки бөлчөк, терс кадимки бөлчөк жана нол саны түрүндө жазууга болот.
- Иррационалдык сандар - санда, ондук жазууда чексиз, мезгилсиз ондук бөлчөктөрдү көрсөтөт.
- Мантисса - сандын бүтүн бөлүгү.
Библиография
1. Множества вещественных чисел: http://life-prog.ru/1_21894_veshchestvennie-chisla.html
2. Видеоурок на тему «Вещественные числа» https://www.youtube.com/watch?v=WrIXyM_rv-Y
3. Видеоурок на тему «Иррациональные числа» https://www.youtube.com/watch?v=W3AyQn6NJ64
4. Видеоурок на тему «Модуль действительного числа и его свойства» https://www.youtube.com/watch?v=KbtNg7n9GpU
1. Алгач араб сандары түз кесиндилерден гана турган, нолдон бөлөгү, “сандардын мааниси алардын жазылышындагы бурчтарына дал келет” принциби боюнча түзүлгөн. Мисалы: нол-бурчу жок, бир-бир бурч, эки-эки бурч ж.б
2. Брахмагупта- индиялык математик, VII кылымда жашаган, биринчилерден болуп оң жана терс сандарды пайдаланган
3. Американын Индиана штатында: штаттын аймагында р санын 4 кө барабар деп эсептөө закону бар.
4. Социализмдин өнүккөн маалында азыктардын баасы алардын белгилерине жараша колдонулган. Эң белгилүү газдуу суусундуктар (Coca-Cola, Fanta, Sprite) 1 с. 49 тый. (0,5л) жана 2с.87 тый. (1л) тураарын ар бир бала билген. Күтүлбөгөн таң калаарлык ачылыш бул биринчи сан экинчинин даражасынан курулган π санын берет. Эскертем, “пи” саны фундаменталдык костанта болуп саналат, “жашоонун константасы” деп айтса да болот.
5. Илимий коомдун көп өкүлдөрү π математикалык константа деп аташат, ал өзүнүн сырлары жана жашыруун маанилери бар сан. Эгерде бир нече изилдөөлөрдү карап көрсөк, бардык кылымдагы жана элдердеги окумуштуулар бул санга көп көңүл бөлүшкөн, ошондуктан биз оңой эле Piсаны жөнүндө эң кызыктуу фактыларды таба алдык жана алардын текс формасы менен видео презентацияларын көрсөтөбүз
Попробуйте ответить правильно на вопросы: