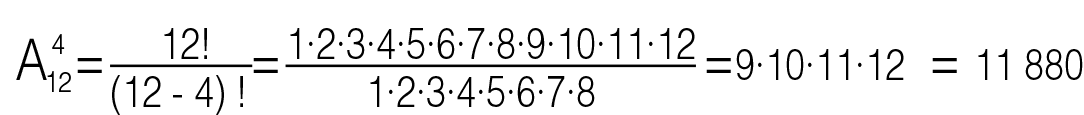БИЛИМ БУЛАГЫ

KR

Математика: Комбинаториканын негиздери — различия между версиями

Строка 3: Строка 3:
 
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content -->  
 
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content -->  
 
{{Якорь|Начало}}
 
{{Якорь|Начало}}
 +
<div class="cutok">[[#Комбинаториканын өнүгүү тарыхынан|Комбинаториканын өнүгүү тарыхынан]] [[#Комбинаторика түшүнүгү|Комбинаторика түшүнүгү]] [[#Комбинаториканын негизги формулалары|Комбинаториканын негизги формулалары]] [[#Ыктымалдуулук. Негизги түшүнүктөр|Ыктымалдуулук. Негизги түшүнүктөр]] [[#Комбинаториканы колдонуу чөйрөсү|Комбинаториканы колдонуу чөйрөсү]] [[#Комбинаторика программалоодо|Комбинаторика программалоодо]]</div>
  
−
Илимдердин ханышасы – математикада, бүт баардык техниканы бир тармакка бириктирген илимди комбинаторика деп айтабыз. 
+
==Комбинаториканын өнүгүү тарыхынан==
−
Комбинаторика — предметтердинкомбинацияларын жана орун алмашууларын окутуп-үйрөтө турган математиканын бир бөлүгү, латындан которгондо combinare – бириктирүү, айкалыштыруу дегенди түшүндүрөт. Эки жарым жүз жыл ичинде жаратылышты окуп-үйрөндүүдө математикалык талдоо негизги ролду ойногон.
 
  
−
Эки жарым жүз жыл аралыгында табиятты окуп-үйрөнүүдө математикалык талдоо негизги ролду ойноп келди. Абал тез ылдамдыкта эсептөөчү машина, компьютерлер пайда болгондон тартып түп тамыры менен өзгөрүлдү. Аларды жардамы менен мурун жүз жана миң жылдап талап калган тапшырмаларды чечип алуу оңойго турду. Дискреттик математиканын гүлдөөсү өзгөрүлүп жана байыркы дискреттик математиканын чөйрөсү – комбинаториканын да ролу өзгөрүлдү. Комбинаторика илим катары VIII кылымдарда пайда болгон, анткени ал учурда ыктымалдуулук теориясы кошо пайда болуп, маселени чыгарылыш ыктымалдуулугу үчүн элементтердин ар түрдүү комбинациясынын санын эсептөө керек болгон.  
+
    Адам баласы биздин заманга чейинки тарыхта эле тиги же бул предметти тандоо, аларды аныкталган тартипте жайгаштыруу, алардын арасынан ар кандай жайгашкандарынын эң ыңгайлуусун издеп табуу, мергенчилиер менчиликте жүрүшүп, жоокерлер – салгылаш учурунда, аспаптарды – жумуш учурунда эң мыкты абалдагысын тандоо сыяктуу маселелерди жолуктурушкан. Кийимдеги жасалгалоо, идиштеги сүрөттөр, жебенин учундагы канаттын сабынын жайгашышы дагы аныкталган ыкма менен кооздолунган. Өндүрүшүк жана коомдук мамилелердин мүмкүнчүлүккө жараша татаалданышы дагы барган сайынтартиби, иерархиясы, топтоштурулушу жөнүндөгү жалпы түшүнүктүн негизинде колдонулуп келген. Кол өнөрчүлүк жана соода-сатыктын өнүгүшү ошол багыт менен өнүгө баштаган. Комбинатордук көндүмдөр эс алуу учурунда да пайдалуу экендиги тастыкталган. Ал чуркоо жарышында, секирүүдө, дискти ыргытуу оюндары учурунда биринчи кезекте эсептөө билгичтигин, пладын ала план курууну жана каршылашынын кадамдарын алдын ала көрө билүү керек болгон.
 +
 
 +
Мындан 35 кылым мурун египеттик фараон Тутанхамонду көмүү зыйнатында пирамидага кошо коюлган предметтердин арасынан байыркы “сенет” оюнунда колдонгон үч горизонт фигурасындагы досканын табылгандыгы. Кийинчерээк шахмат, шашки жана нардалар табылгандыгы. Булар табылган ар бир оюнолуучу фигуралар сунушталган оюнда фигуралардын ары бери жылдырылышы аныкталган айкалышты кармануу менен ким туура билген жана ойногон оюнчу гана натыйжада утушка ээ болоорун түшүнүшкөн.
 +
 
 +
<div class="show-for-large-up">{{center|[[Файл:История развития комбинаторики.mp4|400px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:История развития комбинаторики.mp4|400px]]}}</div>
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
 +
==Комбинаторика түшүнүгү==
 +
 
 +
Комбинато́рика  — дисктреттик объектилерди, көптүктөр (айкалышы, ордун которуусу, жылдырылышы жана элементтерин саноодо) жана алар менен катыштар (айталы, жеке тартипте); латын сөзүнөн combinare которгондо – бириктирүү, айкалышы деп түшүндүрөт. Комбинаторика математиканын башка чөйрөлөрү менен да байланышкан – алгебра, геометрия, ыктымалдуулук теориясы жана билимдин ар түрдүү чөйрөлөрүндө да колдонулат.  
 
        
 
        
−
Сөөк менен ойноодогу ар түрдүү комбинациянын санын эсептөөгө алгачкылардан болуп италиялык математик Тарталья киришкен. Ал  сөөктү канча ыкма менен жүргүзүүгө боло турган таблицаны түзгөн. Бирок ал ар түрдүү ыкма менен бир эле упай алынып калаарын эске алган эмес.Бара бара ар түрдүү оюндар пайда болгон (нарда, карта, шашка, шахмат ж.б.). Ар бир жолу фигуралардын түрдүү айкалыштарын карап, ким утуштуу комбинацияларды жана утулуштан кача билген оюнчу гана ута алганын кароого туура келген.  
+
Жөнөкөй бир мисал карап көрөлү. Мейли, краска куюлган 4 челек бар: кызыл (К), сары (С), жашыл (Ж) жана күрөң (Кң), жана биз аларды коробкаларга ар биринде ар башка эки челектен кылып счалышыбыз керек болот. Биз аны төмөндөгүчө аткарсак болот:
  
−
Белгилүү болгондой, покерде же оролмо оюндарда утуш ыктымалдуулугун эсептөөлөрүн жүргүзүү керек экендигинде, айталы, стрит-флешти 52 картанын ичинен чогултса болоорун. А эсептөөнү комбинаторикасыз жүргүзүү мүмкүн эмес.  
+
<div class="show-for-large-up">{{center|[[Файл:Простой_пример.gif|500px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Простой_пример.gif|400px]]}}</div>
  
−
Эсептөөгө чейин тартипке салуу зарыл .Албетте, иш ордунун ирээтүүлүгүн айтабыз. Биз түшүнө турган комбинациянын санын объектисин тартипке салуу зарыл болот.  Мейли, кызыл түстөгү төрт банкабыз бар: кызыл (К), сары (Ж), жашыл (3) ж/а күрөң (Кор), ар бирин экиден ар башка банкага аларды кутучаларга салыштыруу керек. Биз муну төмөндөгү мүнөздө жасасак болот:
+
Бизде алты ар түрдүү ыкма бар, эгерде бир коробкада сары жана кызыл болсо, анда ал кызыл жана сары челек краска менен бирдей болот. Бирок, эгерде бир түгөй түстөр менен белгилей турган болсок, анда он эки ыкма бар, анткени кызыл-сары түс менен сары-кызылдын айырмасы бар болот.
  
−
<div class="show-for-large-up">{{center|[[Файл:К_ж.png|500px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Простой_пример_1.gif|500px]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:К_ж.png|400px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Простой_пример_1.gif|400px]]}}</div>
  
−
Б.а. алты ар түдүү ыкма менен, бир кутучада сары жана кызыл түстөгү банкалар, ал тиги кызыл жана сары түстөгү банкалар менен бирдей болот. Бирок, түгөй түстөр менен биз желекчелерди боёшубуз керек, анда аны мындай кылуу керек: б.а. 12 ыкма менен; кызыл-сары желекче сары-кызыл менен бирдей болбойт.
+
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
−
<div class="show-for-large-up">{{center|[[Файл:Флаг.png|500px]]}}</div>
+
==Комбинаториканын негизги формулалары==
−
<div class="hide-for-large-up">{{center|[[Файл:Флаг.png|400px]]}}</div>
+
 
 +
'''Правила сложения'''
 +
Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить m + n способами.
  
−
Биздин жашообуз ар түрдүү программалардын көптүгүнөн турат. Тиги же бу тиешелүү программаны иштетиш үчүн туура келген сырсөздү киргизүү керек. Сырсөз катары программанын түрүнө карата сандар, сөздөр же сөздөрдүн айкалышын киргизүүгө туура келет. Комбинаторика музыкада, эмеректик ишмердүүлүктө, ар түрдүү оюндарда колдонулат (нарда, шахмат, шашка) ж.б. Кененирээк окугула: http://ya-znau.ru/znaniya/zn/80, а эгерде маселе чыгаргыңар келсе анда бул жакка өткүлө: http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html
+
'''Пример 1.'''
 +
На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
  
−
<div class="show-for-large-up">{{center|[[Файл:Комбинаториканы_колдонуу.png|500px]]}}</div>
+
'''Чыгарылышы:'''
−
<div class="hide-for-large-up">{{center|[[Файл:Комбинаториканы_колдонуу.png|400px]]}}</div>
+
По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу сложения, можно осуществить 5 + 4 = 9 способами.
  
−
<div class="show-for-large-up">{{center|[[Файл:Кошуу_эрежеси.png|500px]]}}</div>
+
'''Ответ''': 9 способов.
−
<div class="hide-for-large-up">{{center|[[Файл:Кошуу_эрежеси.png|400px]]}}</div>
 
  
−
'''1 мисал'''
+
'''Пример 2.'''  
−
Тарелкада 5 алма жана 4 апельсин салынган. Канча ыкма менен бир жемишти тандоого болот.
+
Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза?
−
'''Чыгарылышы:'''
 
−
Тапшырманын шарты боюнча алманы 5 ыкма, ал эми апельсинди 4 ыкма менен тандоого болот. Тапшырманын шарты болсо “же алма же пельсин” экендигин эске алуу менен 5+4=9 экенин табууга болот.
 
−
'''Жообу:''' 9 ыкма.
 
  
−
'''2 мисал'''
+
'''Чыгарылышы''':  
−
1,4,7 сандарынан ар бири бир жолудан көп эмес колдонуп, канча эки маанилүү сан куроого болот?
+
'''1 способ: перебор вариантов.'''
−
'''Чыгарылышы:'''
+
Для того, чтобы не пропустить и не повторить ни одно из чисел, будем записывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4, и, наконец, с цифры 7:
−
'''1 ыкма''' Варианттарды тандоо.
 
−
Өткөрүп жибербес жана кайталабас үчүн бул сандарды өсүү тартибинде жазабыз. Алгач, 1 санына башталгандарды, андан сөн 4 жана 7 санына башталган сандарды жазабыз:
 
 
14, 17, 41, 47, 71, 74.
 
14, 17, 41, 47, 71, 74.
−
'''Жообу:''' 6 сан.
 
  
−
'''2 ыкма:''' Мүмкүн болгон вариантту дарак.
+
'''Ответ''': 6 чисел.
−
Бул тапшырманы чыгаруу үчүн атайын схема курулган. 
 
−
Жылдызча коёбуз. Андан ары ал жылдызчадан 3 кесинди чыгарабыз. Тапшырманын шарты боюнча 3 сан берилген – 1,4,7, кесиндинин учтарына бул сандарды жазабыз.
 
−
Андан соң, ар бир санга 2ден кесинди туташтырабыз. Алардан ары улап ар бир кесиндинин учуна 1, 4, 7 сандарын жазабыз. Жыйынтыгы: 14, 17, 41 47, 71, 74 болот. Б. А. баары 6 сан болот. Бул схема даракка окшош болгондуктан “дарак” деп аталат.  
 
  
−
<div class="show-for-large-up">{{center|[[Файл:47.png|500px]]}}</div>
+
'''2 способ: дерево возможных вариантов.'''
−
<div class="hide-for-large-up">{{center|[[Файл:47.png|400px]]}}</div>
+
Для этой задачи построена специальная схема.
 +
Ставим звездочку. Далее отводим от звездочки 3 отрезка. Так как в условии задачи даны 3 цифры – 1, 4, 7, то на концах отрезков ставим  цифры 1, 4, 7.
 +
Далее от каждой цифры проводим по 2 отрезка. На концах этих отрезков записываем также цифры 1, 4, 7. Получились числа: 14, 17, 41 47, 71, 74. То есть всего получилось 6 чисел. Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола.
  
 +
<div class="show-for-large-up">{{center|[[Файл:Пример 2 2 способ.gif|500px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Пример 2 2 способ.gif|400px]]}}</div>
  
−
'''3 мисал'''  
+
'''Правила умножения'''
−
1,4,7 сандарынан ар бири бир жолудан көп эмес колдонуп, канча эки маанилүү сан куроого болот?
+
Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить m ∙ п способами.
−
'''Чыгарылышы'''
 
−
Биринчи эки орунду санды үч ыкма менен тандоого болот. Биринчи санды тандагансоң, экинчи санды калган сандардан эки ыкма менен тандаса болот. Андан соң, изделүүчү үч маанилүү сандын жалпы саны 3*2 санын көбөйтүндүсүнө, бюаю 6га барабар болот.  искомых трехзначных чисел равно произведению 3∙2, т.е. 6.
 
−
'''Жообу:''' 6 сан.
 
  
−
<div class="show-for-large-up">{{center|[[Файл:Факториалдын_таблицасы.png|500px]]}}</div>
+
''Пример 3.''
−
<div class="hide-for-large-up">{{center|[[Файл:Факториалдын_таблицасы.png|400px]]}}</div>
+
Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза?
  
−
<div class="show-for-large-up">{{right|[[Файл:Доска.png|200px]]}}</div>
+
'''Чыгарылышы''':
−
<div class="hide-for-large-up">{{right|[[Файл:Доска.png|200px]]}}</div>
+
Первую цифру двузначного числа можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать из оставшихся цифр уже двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 3∙2, т.е. 6.
−
'''Которулуштуруу''' деп элементтери тартиби менен жайгашкан көптүк аталат. N элементтен турган мүмкүн болушунча которулуштуруу бул формула менен эсептелинет:  '''Pn = n!'''
 
  
−
'''4 мисал.'''   
+
'''Ответ''': 6 чисел.
−
Финалдык чуркоодогу 8 катышуучу 8 чуркоочу тилкеге канча ыкма менен которулууга болот?  
+
 
−
'''Чыгаралышы.'''
+
'''Факториал'''.
 +
Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n. Обозначение n!
 +
 
 +
0! = 1
 +
 
 +
1!=1
 +
 
 +
2! = 1∙ 2 = 2
 +
 
 +
3! =  1∙ 2 ∙ 3 = 6
 +
 
 +
4! = 1∙ 2 ∙ 3 ∙ 4 =24
 +
 
 +
5! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120
 +
 
 +
6! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720
 +
 
 +
7! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 = 5 040
 +
 
 +
8! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 = 40 320
 +
 
 +
9! =  1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 ∙ 9 = 362 880
 +
 
 +
10! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 ∙ 9 ∙ 10 = 3 628 880
 +
 
 +
'''Свойства комбинаторики: перестановки, сочетание, размещение'''
 +
 
 +
<div class="show-for-large-up">{{center|[[Файл:Шахматная_доска_абстрация.jpg|500px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Шахматная_доска_абстрация.jpg|400px]]}}</div>
 +
 
 +
Перестановкой называется конечное множество, в котором установлен порядок элементов. Число всевозможных перестановок из n элементов вычисляется по формуле:  Pn = n!
 +
 
 +
'''Пример 4.''' 
 +
Сколькими способами могут быть расставлены восемь участниц финального забега на восьми беговых дорожках?
 +
 
 +
'''Чыгарылышы.'''
 
P8 = 8! = 40 320
 
P8 = 8! = 40 320
  
−
<div class="show-for-large-up">{{center|[[Файл:Различие между перестановками.png|500px]]}}</div>
+
Размещением  А<sup>k</sup><sub>n</sub>    из n элементов конечного множества по k, где  k≤n, называют упорядоченное множество, состоящее из k элементов и вычисляется по формуле: 
−
<div class="hide-for-large-up">{{center|[[Файл:Различие между перестановками.png|400px]]}}</div>
+
 
 +
<div class="show-for-large-up">{{center|[[Файл:Формула_размещения.png|100px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Формула_размещения.png|100px]]}}</div>
 +
 
 +
'''Пример 5.'''
 +
 
 +
Из 12 учащихся нужно отобрать по одному человеку для участия в городских олимпиадах по математике, физике, истории и географии. Каждый из учащихся участвует только в одной олимпиаде. Сколькими способами это можно сделать?
 +
 
 +
'''Решение'''.
 +
 
 +
<div class="show-for-large-up">{{center|[[Файл:Пример № 5.png|500px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Пример № 5.png|400px]]}}</div>
 +
 
 +
Подмножества, составленные из n элементов данного множества и содержащие k элементов в каждом подмножестве, называют сочетаниями из n элементов по k. (Сочетания различаются только элементами, порядок их не важен: ab и ba – это одно и тоже сочетание) и вычисляется по формуле:  .
 +
 
 +
<div class="show-for-large-up">{{center|[[Файл:Формула_сочетаний.png|100px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Формула_сочетаний.png|100px]]}}</div>
 +
 
 +
Число размещений, перестановок и сочетаний связаны равенством:  .
 +
 
 +
<div class="show-for-large-up">{{center|[[Файл:Число размещений, перестановок и сочетаний.png|100px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Число размещений, перестановок и сочетаний.png|100px]]}}</div>
 +
 
 +
Различие между перестановками, размещениями, сочетаниями:
 +
В случае перестановок берутся все элементы и изменяется только их местоположение.
 +
В случае размещений берётся только часть элементов и важно расположение элементов друг относительно друга.
 +
В случае сочетаний берётся только часть элементов и не имеет значения расположение элементов друг относительно друга.
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
 +
==Ыктымалдуулук. Негизги түшүнүктөр==
 +
Ыктымалдуулук теориясында бир нече жолу кубулуштарды, тажрыйбаларды, эксперименттерди байкоо текшрүү (сыноо) деп аталат. Текшерүү (сыноонун) жыйынтыгын окуя деп айтабыз. Мисалы, экзамен тапшыруу- бул сыноо; аныкталган баа алуу – бул окуя, оюн кубикти ыргытуу же өкчөө – бул сыноо; тиги же бул тараы менен түшүү же упайдын саны – бул окуя.
 +
 
 +
Ыктумалдуулук – бул окуянын пайда болуш мүмкүндүгүн мүнөздөөчү сан. Ар бир мүмкүн болгон сыноонун жыйынтыкгы элементардык жыйынтык деп аталат.
  
−
==Тапшырма==
+
Рнын ыктымалдуулугу А окуясынын ошол окуяга карата боло (ишке аша) турган сандын, баардык мүмкүн болгон элементардык жыйынтыкка дал келбеген жалпы топту түзүүчү катышы болот. Р ыктымалдуулук А окуясын Р = m/n , мында m- элементардык жыйынтык; n – сыноодогу баардык мүмкүн болгон элементардык жыйынтыгы, Анын ылайыктуу элементардык жыйынтыгын аныктоочу формула.
−
'''«Карышкыр, эчки жана капуста»'''
 
−
<div class="show-for-large-up">{{right|[[Файл:Задача_волк.png|300px]]}}</div>
 
−
<div class="hide-for-large-up">{{right|[[Файл:Задача_волк.png|400px]]}}</div>
 
−
Дыйкан дарыянын аркы өйүзүнө карышкырды, эчкини жана капустаны алып өтүшү керек. Кайыкта орундук аз болгондуктан өзү менен кошо бирөөнү: карышкырды, эчкини же капустаны гана алып өтө алат. Бирок, карышкырды эчки менен калтырса карышкыр эчкини жеп салат, ал эми эчкини капуста менен калтырса капустаны эчки да жеп салат. Дыйкан эмне кылуу керек?
 
  
−
Маселени чыгаруу үчүн маселенин коюлуш шартына карата элементтерди өз ара жайгаштырууну колдонуу керек. Дыйкан бул жерде эчкини алып өтүү менен башташ керек болот. Андан соң жээке келип карышкырды тиги жээке алып келип кайра өзү менен кошо эчкини берки жээке ала кетиши керек болот. Ал жактан эчкини таштап капустаны тиги карышкыр турган жээкке алып келиш керек. Андан соң кайтып келип эчкини алып өтөт.  
+
Маселе
 +
Алты бирдей жасалган корточкага К, Б, И, К, Е, Ш тамгалары жазылган. Карточкалар аралаштырылып кокустук боюнча бир катарга тизилет. Натыйжада БИШКЕК деп жазылып калгандай ыктымалдуулук эмнеге барабар болоорун тапкыла.
  
−
'''«Крестиктер-нөлдөр»'''
+
<div class="show-for-large-up">{{center|[[Файл:Задача_Бишкек.gif|500px]]}}</div>
−
<div class="show-for-large-up">{{right|[[Файл:Задача_крестики.png|300px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Задача_Бишкек.gif|400px]]}}</div>
−
<div class="hide-for-large-up">{{right|[[Файл:Задача_крестики.png|400px]]}}</div>
 
−
Эң белгилүү байыркы оюн. Квадратта 9 клеткага чийилген, оюнчулар кезеги менен бош клеткаларга крестик жана нөлдөрдү бир ктарга 3өө болгондой кылышып чийишет, толтурушат. Муну биринчи жасаган жеңишке ээ болот.
 
−
Эгерде катасы жок толтурушса анда оюн тең-тең эсеби мене аяктайт. Каршылашың ката толтурган гана убакта утушка ээ болосуң. Эң туура жүрүш – бурчтагы клеткаларды ээлөө.  Эгерде каршылашың сага жооп кылып ортоңку келтканы толтурса, анда анын утулганы.
 
  
−
'''«Ним»'''
+
'''Чыгарылышы'''.
−
<div class="show-for-large-up">{{right|[[Файл:Задача_гвоздики.png|300px]]}}</div>
+
Изделүүчү ыктымалдуулук Р = m/n , мында m- элементардык жыйынтык; n – сыноодогу баардык мүмкүн болгон элементардык жыйынтыгы формуласы менен эсептелинет.
−
<div class="hide-for-large-up">{{right|[[Файл:Задача_гвоздики.png|400px]]}}</div>
+
 
−
Мейли бир же бир нече топтогу предеттер болсун. Оюнчулар топтордон төмөнкү эрежеге ылайык кезеги менен предметтерди алышат: канча сандагы предметти бир нече топтордон бир гана жолу алууга уруксаат берилет. Көпчүлүккө белгилүү болгон жана жеңишке алып барган оюндун бир нече варианты бар.  
+
Биздин учурда n = 6! = 720 (6 карточканын жайгаштырылыш саны);
 +
 
 +
m = 2 (бул сөздөгү “К” тамгасынын эки жолу кайталанышы, калгандары бирден эле жолу).
 +
 
 +
Тыянак, Р=2/720=1/360.
 +
 
 +
'''Задача «Волк, козел и капуста»'''
 +
 
 +
Крестьянину нужно перевезти через реку волка, козла и капусту. Лодка так мала, что в ней кроме крестьянина может поместиться только или волк, или козел, или капуста. Но если оставить волка с козлом, он его съест, а если оставить козла с капустой, то будет съедена капуста. Как быть крестьянину?
 +
 
 +
Для решения требуется расположить путем взаимной перестановки элементов и в соответствии с условием задачи в определенном порядке. Крестьянину следует начать переправу с перевозки козла. Затем он возвращается и берет волка, которого перевозит на другой берег и оставляет там, а козла возвращает назад на предыдущий берег. Оттуда забирает капусту и перевозит ее к волку. А затем возвращается и забирает козла.
 +
 
 +
<div class="show-for-large-up">{{center|[[Файл:Задача_Волк_коза_капутса.gif|500px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Задача_Волк_коза_капутса.gif|400px]]}}</div>
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
 +
==Комбинаториканы колдонуу чөйрөсү==
 +
 
 +
Комбинатордук маселелерди чыгаруу бирге дайыма керек болот. Мисалы, филологго канча тамгалардын айкалышын эске алуу керек болот? Үч ар түрдүү кездемеден модельер канча ар түрдүү кийимди ойлоп табууга болот? Сатып алуучу буюмдардын тизмесин, сабактардын жүргүртмөсүн, футболдук команданын, Рубик кубигин, тамакты даярдоодо, класста окуучуларды отургузуу, текчелерге китептерди жайгаштыруу, столду жасалгоолоодо кантип түзүү керек? Көпчүлүк балдар оюндары чучу кулак кармоо менен башталат. Карта менен, ширенке менен же ромашка менен төлгө ачуу дагы комбинаторикага негизделген. Крек болсо поэзия дагы комбинаториканы унутта калтырбайт! Ыр жана музыка, графика – живопись  искусствосу – мунун баары комбинаторжук процесстер. Бекеринен бул чөйрөдөгү “компьютерлер” таң калаардыктай ийгиликтерге жетишпесе керек. Аягында, баардык адамдар – ДНК молекуларларындагы гендердин комбинациялары экенин айтса болот.
 +
 
 +
<div class="show-for-large-up">{{center|[[Файл:Применение_комбинаторики.mp4|500px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Применение_комбинаторики.mp4|400px]]}}</div>
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
 +
==Комбинаторика программалоодо==
 +
'''Комбинаторика''' – бул ар кандай алгоритмдерди талдоодо, оптималдуу стратегияларды тандоодо керек болгон программисттердин чыныгы кенчи. Комбинатордук формулалар ыктымалдуулукту эсептөө үчүн, өзүнүн учурунда статистикалык гипотезаларды текшерүү үчүн керек болот. Программисттер комбинатордук маселелерди чыгарууда генерациялоо үчүн өзгөчө көңүлдү Generics Combinatorics программасы колдонгон пандигиталдык сандарга бурат.
 +
 
 +
Пандигиталдык сан деп, нөлдөн башталбаган жана бир сан кайра кайталанбаган сандарды айтабыз. Мисала 123456789.
 +
 
 +
Пандигиталдык сандары бар маселелерди логикалык сыяктуу эле керек болсо андан да жөнөкөй чыгарылат, анткени комбинатордук объектилер өзүнө сандарды камтыйт.
 +
 
 +
Число 123456789 — наименьшее пандигитальное число в десятичной системе счисления. При умножение на 8 результатом будет 987654312 — другое пандигитальное число, близкое к палиндрому исходного, за исключением двух последних цифр, обменявшихся местами. Это число также сохраняет свою пандигитальность при умножении:
 +
 
 +
- 2ге  123456789 ∙ 2 = 246913578,
 +
 
 +
- 4кө  123456789 ∙ 4 = 493827156,
 +
 
 +
- 5ке  123456789 ∙ 5 = 617283945,
 +
 
 +
- 7ге 123456789 ∙ 7 = 864197523.
 +
 
 +
Мисал катары башка санды санга 2, 4, 5, жана 7 (коэффициентке) көбөйтүүдө пандигиталдуулугун сактаган сан катары 1098765432 келтирсек болот. Эгерде 123456789ны 8ге жана 9га көбөйтсөк бул сандын толук палиндрому келип чыгат. Эгерде көбөйүүчүнү жана кошулуучуларды 1ге чоңойтсок, жыйынтыгы ондо экиге чейинки разраддагы 1 1диктен турган сан пайда болот. 
 +
 
 +
<div class="show-for-large-up">{{center|[[Файл:Пандигитальные_квадраты.gif|500px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Пандигитальные_квадраты.gif|400px]]}}</div>
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
 +
==Полезные ссылки==
 +
Вся наша жизнь состоит из множества разнообразных программ. Чтобы запустить ту или иную программу нужно ввести соответствующий верный пароль. В качестве кода в зависимости от рода программы могут выступать всевозможные цифры, слова или комбинации слов, поведение или действие. Комбинаторика используется в музыке, в мебельной деятельности, в различных играх (нарды, шашки, шахматы) и т.д. Читайте подробнее:  [Электронный ресурс] //  2011-2017 Сила знаний URL:  http://ya-znau.ru/znaniya/zn/80    (Дата посещения: 19.04.2018)
 +
 
 +
Толук чыгарылыштуу комбинатордук маселелерди төмөндө караса болот:
 +
[Электрондык ресурс] //mathprofi.ru, Александр Емелин, 2010-2018  URL: http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html (Катышуу датасы: 19.04.2018)
 +
 
 +
Необходимые теоретические сведения и формулы для решения комбинаторных задач школьного уровня можно посмотреть здесь: [Электронный ресурс] //  Харламов А.В. элементы комбинаторики, 2016г. // URL:  http://elibrary.sgu.ru/uch_lit/1626.pdf (Дата посещения: 21.04.2018)
 +
 
 +
Поиграем? Пусть имеется одна или несколько групп предметов. Играющие берут по очереди предметы из групп по правилам, которые заранее устанавливают: какое количество предметов разрешается брать за один раз и из скольких групп. Существует множество вариантов игры, и для большинства известна наилучшая стратегия, ведущая к выигрышу.:[Электронный ресурс] // ЮЦ «Восстание-6» URL: https://logic-games.spb.ru/nim/ (Дата посещения: 22.04.2018)
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
 
==Глоссарий==
 
==Глоссарий==
−
'''Комбинаторика''' - предметтердин орун алмашышын жана комбинациясын окуп-үйрөтө турган математиканын бир бутагы.
+
'''Дискре́ттүүлү''' (лат. discretus — бөлүнгөн, үзгүлтүктүү) – үзгүлтүксүзгө карама-каршы коюлган, үзгүлтүктүү касиет. Дискреттүүлүк түшүнүгү: бин нече туруктуу абалдардын ортосундагы өзгөрүүчү бин нерсе, мисалы мүнөттүк жебечеси дискреттүү кыймылдаган механикалык сааты, 1/60га айлананын бөлүгү; өзүнчө бөлүктөрдү түзгөн, үзгүлтүктүү, бөлчөктүк бир нерсе.
 +
 
 +
'''Палиндро́м''' (грек. πάλιν — «артка, кайра» жана башка.-грек. δρóμος — «чуркоо, кыймыл»)— эки тарабынан бирдей окула турган сан, тамгалар айкалышы, сөз же текст.
  
−
== Библиография ==
+
'''Пандигиталдык сандар''' – бул нолдөн баштабаган жана бир сан кайра кайталанбаган сан.
−
*Комбинаторика. https://infourok.ru/kombinatorikaeto-interesnonauchniy-proekt-sekciya-matematika-816469.html
 
−
*Комбинаторика: основные правила и формулы. http://ya-znau.ru/znaniya/zn/80
 
−
*Савельев Л.Я. Комбинаторика и вероятность. – Новосибирск, Наука, 1975.
 
−
*Тюрин Ю.Н., Макаров А.А., Высоцкий И.Р., Ященко И.В. Теория вероятностей и статистика. – М.: МЦНМО: АО «Московские учебники», 2004.
 
  
 +
'''Су́тра''' (санскр. सूत्र sūtra IAST, «жип», пали: sutta) — байыркы абадияттардагы лаконикалык жана үзгүлтүктүү айтылыш, афоризмдер, кийинчерээк – ушундай айтылыштардын. Сутраларда ар түрдүү билимдери, дээрлик Байыркы Индиянын диний-философиялык окуучлары жазылган. 
  
−
<div class="light" style="float:right;>[[#Начало|В начало]]</div>
+
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
 +
== Библиография ==
 +
*Комбинаторика: основные правила и формулы. : [Электронный ресурс] //  2011-2017 Сила знаний URL:  http://ya-znau.ru/znaniya/zn/80  (Дата посещения: 19.04.2018)
 +
*Задачи по комбинаторике. Примеры решений.: [Электронный ресурс] //mathprofi.ru, Александр Емелин, 2010-2018  URL: *http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html    (Дата посещения: 19.04.2018)
 +
*Сканворды, кроссворды и головоломки: [Электронный ресурс] //  Пискунов Алексей © 2009-2018 http://www.graycell.ru/index.html (Дата посещения: 19.04.2018)
 +
*Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика: М.: ФИМА, МЦНМО, 2006. — 400 с.
 +
*Мир математики: в 40 т. Т.21: Ламберто Гарсия дель Сид. Замечательные числа. Ноль, 666,  и другие бестии./Пер. с исп. –М.: Де Агостини, 2014. – 160 с.
 +
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 
</div>
 
</div>
  
Строка 113: Строка 247:
 
<div class="shadow radius sbstyle">
 
<div class="shadow radius sbstyle">
 
<div class="row">
 
<div class="row">
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Комбинаторика айланабызда</div>
+
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Комбинаторика вокруг нас</div>
 
</div>
 
</div>
−
1. Мындан 35 кылым мурун египеттик фараон Тутанхамондун сөөгү коюлган пирамидада предметтердин арасынан байыркы“сенет” оюну үчүн үч горизоталдуу тактаны табышкан. Кийинчерээк нарданы, шашканы жана шахматты.  
+
Математика – жөнөкөй эрежелерге ылайык жана мааниге анча деле ээ эмес белгилөөлөрду колдонуу менен ойнолуучу жөн гана оюн.
 +
                      Давид Гильберт
 +
 
 +
 
 +
Оюн ырахат жана кубаныч эле тартуулабастан, толук кандуу эс алуу менен кошо интеллектти машыктырууга үйрөтөт. Математиканын жетишкендиктерин колдонуу жаңы оюндардын теориясын андан ары өнүктүрүү үчүн жана жаңы машыктырууча маселелерди түзүүдө кзмат кылаарын ырахат менен ырастоого болот.
 +
 
 +
'''Кубик Рубика''' – это куб, как бы разрезанный на 27 одинаковых кубиков. В исходном положении каждая грань куба окрашена в один из 6 цветов. Остроумный механизм позволяет поворачивать любой слой из 9 кубиков, примыкающий к одной грани куба, вокруг ее центра. При этом цвета граней смешиваются. Задача состоит в том, чтобы вернуть разноцветные грани кубика в исходное положение. Теоретически из любого состояния кубика можно вернуться в исходное, не более чем за 23 хода.  
  
−
2. Алгачкы комбинаторикага жакын делинген кездешүүлөрдү кытайдын “Өзгөрмө китеби” колжазмаларынан жолуктурууга болот.
+
{{center|[[Файл:РЕБЕНОК_ГЕНИЙ_собрал_кубик_Рубика_за_7_секунд.mp4|450px|start=1]]}}
  
−
3. Комбинаториканын өнүгүшүнө өзгөчө секирикти кумар оюнчары болгон сөөк оюндары түрткү берген.  
+
Лучшее время, показанное на чемпионате мира 1982 г. по скоростной сборке кубика Рубика, составило всего 22,95 секунды. А в наше время дети собирают за считанные секунды. Давайте убедимся
  
−
4. Комбинаториканын ыкмасы менен тексттин үстүнөн комбинациялардын кайталаныш окшоштугун байкоодо эсептөөгө болгон.
+
'''Жебечелер'''
  
−
5. Рубик кубиги – бул 27 бирдей кубка бөлүнгөн куб. Алгачкы абалында кубдун ар бир кырлары 6 түстүн бири менен боёлгон. Курч акылдуу механизм анын борбору менен кесилишкен каалагандай 9 кубиктин катмарын которууга мүмкүндүк берет. Мында чектеринин түстөрү аралашат. Маселе түрдүү түстөгү кубиктин кырларын алгачкы абалга алып келүүдө жатат. Теориялык жактан кубиктин каалагандай абалынан алгачкы абалына 23 жүрүштөн ашык эмес жүрүш менен келүүгө болот.  
+
Ар бир клеткадагы сандардан алардын саны алгачкы санга тең болуп, мында торчодогу сан эсепке алынбагандай кылып жебечелерди жүргүзүү керек. Жебечелер тигинен жана туурасынан жүргүзүлүшү керек. Жебечелер баардык бош клеткаларда болушу керек.  
  
−
<div class="show-for-large-up">{{center|[[Файл:Кубик_рубик.png|450px]]}}</div>
+
{{center|[[Файл:Стрелочки.gif]]}}
−
<div class="hide-for-large-up">{{center|[[Файл:Кубик_рубик.png|450px]]}}</div>
 
  
−
</div>
+
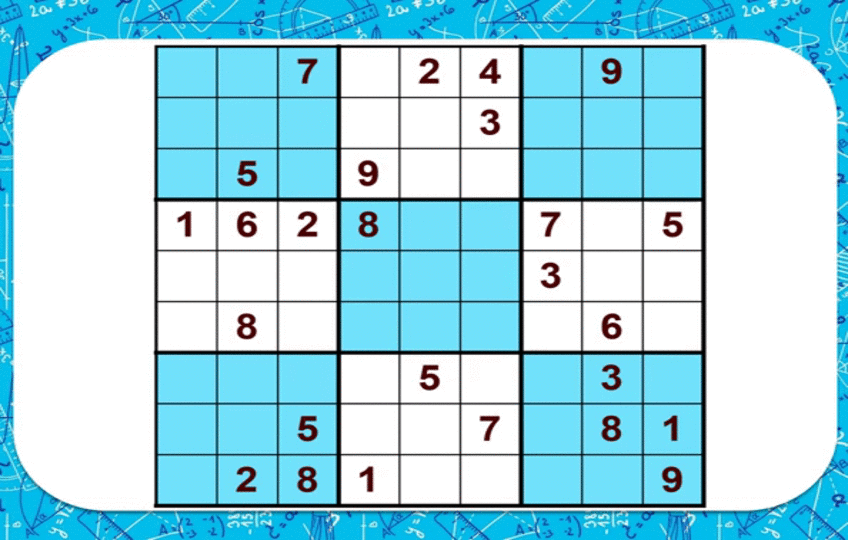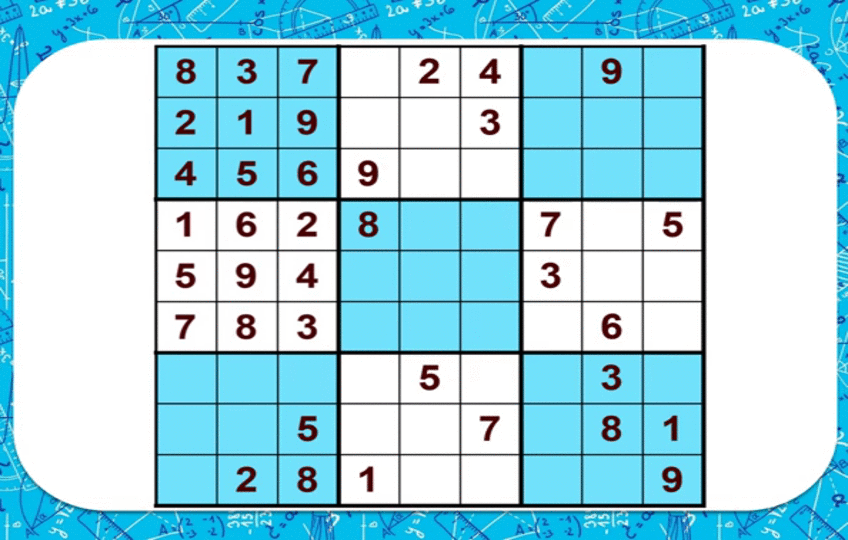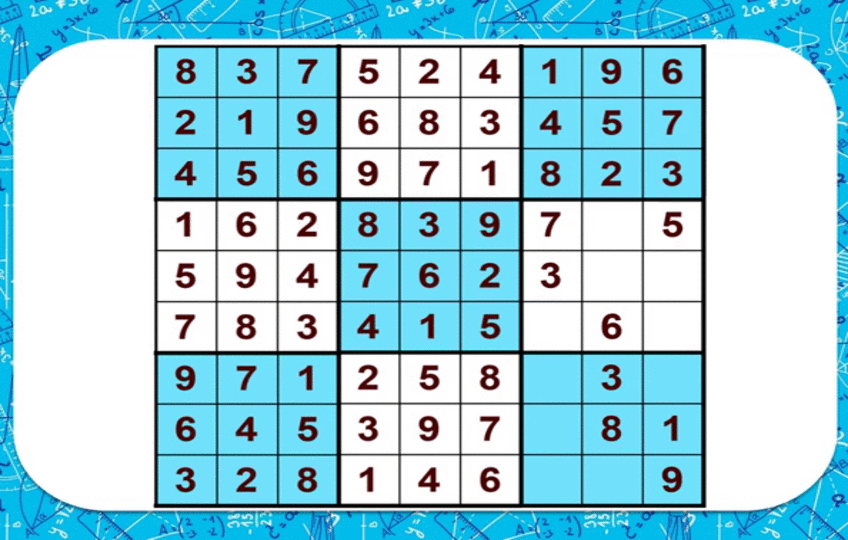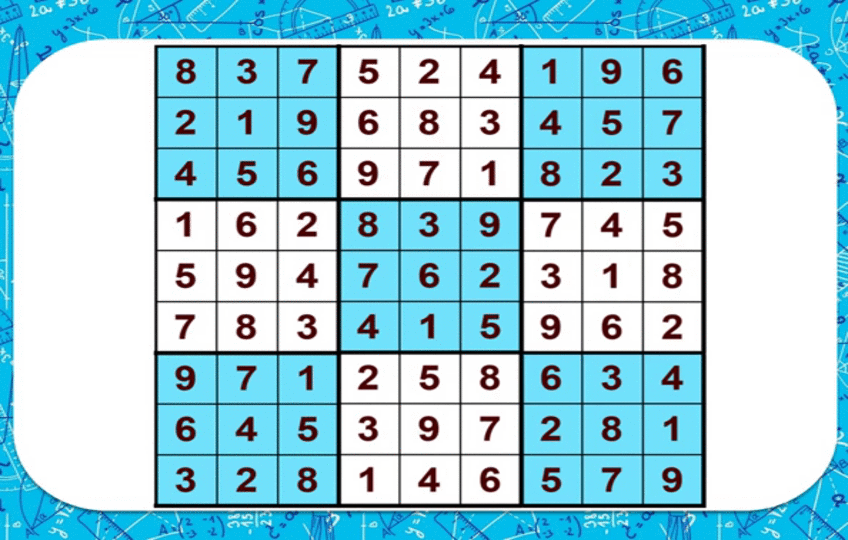
'''Судоку'''
 +
 
 +
1ден 9га чейинки сандардын бош торчосунда ар бир сапчадагы, ар бир мамычадагы жана ар бир квадраттагы сандар бирден гана жолу кездешкендей жайгаштыруу керек.
 +
 
 +
{{center|[[Файл:Судоку_.gif]]}}
 +
 
 +
'''Лесенка'''
  
 +
Пирамиданын чокусунан негизине чейинки сандары ар башка болгондой жолду табуу керек.
  
−
<!-- четвертый элемент сайдбара лайфхак -->
+
{{center|[[Файл:Лесенка.gif]]}}
−
<div class="shadow radius sbstyle" style="margin-top:20px;">
 
−
<div class="row">
 
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Сизчи?</div>
 
−
</div>
 
  
−
Мурун 1982-жылы дүйнөлүк чемпионатта Рубик кубигин чогултуунун ылдамдыгын 22,95 секунд деп көрсөткөн. А биздин учурда болсо  балдарыбыз аз эле секунддада чогултат. Келгиле ынанып көрөлү
+
'''Пирамида'''
  
−
<div class="show-for-large-up">{{center|[[Файл:РЕБЕНОК_ГЕНИЙ_собрал_кубик_Рубика_за_7_секунд.mp4|450px]]}}</div>
+
Уячалардын 1ден 9га чейин төмөнкү эрежеге ылайык толтуруу керек: уячадагы сан төмөнкү эки уячадагы сандардын суммасы же айырмасы катары болуп, пиармиданын ар бир сабындагы сандар кайталнбашы керек.
−
<div class="hide-for-large-up">{{center|[[Файл:РЕБЕНОК_ГЕНИЙ_собрал_кубик_Рубика_за_7_секунд.mp4|450px]]}}</div>
 
  
−
<div class="show-for-large-up">{{center|[[Файл:11_комбинаторика.png|450px]]}}</div>
+
{{center|[[Файл:Пирамида.gif]]}}
−
<div class="hide-for-large-up">{{center|[[Файл:11_комбинаторика.png|450px]]}}</div>
 
  
−
<div class="show-for-large-up">{{center|[[Файл:88_комбинаторика.png|450px]]}}</div>
+
'''Крестики-нолики'''
−
<div class="hide-for-large-up">{{center|[[Файл:88_комбинаторика.png|450px]]}}</div>
+
Самая известная древняя игра. В квадрате, разделенном на девять клеток, игроки по очереди ставят в свободную клетку свой знак: крестик или нолик, стараясь выстроить три крестика или три нолика подряд. Тот, кто первым сделает это, тот и выигрывает.
  
−
</div>
+
Если не делать ошибок, то игра оканчивается в ничью. Выиграть можно только в том случае, если противник ошибется. Самый правильный ход –занять угловую клетку. И если партнер не ответит на это своим знаком в центре, то он проиграл.
  
 +
{{center|[[Файл:Крестики_нолики.gif]]}}
  
 
<!-- четвертый элемент сайдбара лайфхак -->
 
<!-- четвертый элемент сайдбара лайфхак -->
 
<div class="shadow radius sbstyle" style="margin-top:20px;">
 
<div class="shadow radius sbstyle" style="margin-top:20px;">
 
<div class="row">
 
<div class="row">
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Ребусту тапкыла</div>
+
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Ребусы</div>
 
</div>
 
</div>
  
−
1.
+
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
−
<div class="show-for-large-up">{{center|[[Файл:Ребус1_комбинаторика.png|450px]]}}</div>
+
  <li class="active">
−
<div class="hide-for-large-up">{{center|[[Файл:Ребус1_комбинаторика.png|450px]]}}</div>
+
    [[file:Ребус_№_1_.png|300px]]
−
2.
+
  </li>
−
<div class="show-for-large-up">{{center|[[Файл:Ребус2_комбинаторика.png|450px]]}}</div>
+
<li>
−
<div class="hide-for-large-up">{{center|[[Файл:Ребус2_комбинаторика.png|450px]]}}</div>
+
    [[file:Ребус_№_2.png]]
−
3.
+
  </li>
−
<div class="show-for-large-up">{{center|[[Файл:Ребус3_комбинаторика.png|450px]]}}</div>
+
<li>
−
<div class="hide-for-large-up">{{center|[[Файл:Ребус3_комбинаторика.png|450px]]}}</div>
+
    [[file:Ребус № 3 Комбинаторика.png]]
−
4.
+
  </li>
−
<div class="show-for-large-up">{{center|[[Файл:Ребус4_комбинаторика.png|450px]]}}</div>
+
<li>
−
<div class="hide-for-large-up">{{center|[[Файл:Ребус4_комбинаторика.png|450px]]}}</div>
+
    [[file:Ребус_№_4_.png]]
−
5.
+
  </li>
−
<div class="show-for-large-up">{{center|[[Файл:Ребус5_комбинаторика.png|450px]]}}</div>
+
<li>
−
<div class="hide-for-large-up">{{center|[[Файл:Ребус5_комбинаторика.png|450px]]}}</div>
+
    [[file:Ребус_№_5_.png]]
 +
  </li>
 +
</ul>
 
</div>
 
</div>
  
−
Жооптор:
+
Ответы:
  
 
# Вариант
 
# Вариант

Версия 17:23, 7 мая 2018

Комбинаториканын өнүгүү тарыхынан Комбинаторика түшүнүгү Комбинаториканын негизги формулалары Ыктымалдуулук. Негизги түшүнүктөр Комбинаториканы колдонуу чөйрөсү Комбинаторика программалоодо

Комбинаториканын өнүгүү тарыхынан

   Адам баласы биздин заманга чейинки тарыхта эле тиги же бул предметти тандоо, аларды аныкталган тартипте жайгаштыруу, алардын арасынан ар кандай жайгашкандарынын эң ыңгайлуусун издеп табуу, мергенчилиер менчиликте жүрүшүп, жоокерлер – салгылаш учурунда, аспаптарды – жумуш учурунда эң мыкты абалдагысын тандоо сыяктуу маселелерди жолуктурушкан. Кийимдеги жасалгалоо, идиштеги сүрөттөр, жебенин учундагы канаттын сабынын жайгашышы дагы аныкталган ыкма менен кооздолунган. Өндүрүшүк жана коомдук мамилелердин мүмкүнчүлүккө жараша татаалданышы дагы барган сайынтартиби, иерархиясы, топтоштурулушу жөнүндөгү жалпы түшүнүктүн негизинде колдонулуп келген. Кол өнөрчүлүк жана соода-сатыктын өнүгүшү ошол багыт менен өнүгө баштаган. Комбинатордук көндүмдөр эс алуу учурунда да пайдалуу экендиги тастыкталган. Ал чуркоо жарышында, секирүүдө, дискти ыргытуу оюндары учурунда биринчи кезекте эсептөө билгичтигин, пладын ала план курууну жана каршылашынын кадамдарын алдын ала көрө билүү керек болгон.

Мындан 35 кылым мурун египеттик фараон Тутанхамонду көмүү зыйнатында пирамидага кошо коюлган предметтердин арасынан байыркы “сенет” оюнунда колдонгон үч горизонт фигурасындагы досканын табылгандыгы. Кийинчерээк шахмат, шашки жана нардалар табылгандыгы. Булар табылган ар бир оюнолуучу фигуралар сунушталган оюнда фигуралардын ары бери жылдырылышы аныкталган айкалышты кармануу менен ким туура билген жана ойногон оюнчу гана натыйжада утушка ээ болоорун түшүнүшкөн.

В начало

Комбинаторика түшүнүгү

Комбинато́рика — дисктреттик объектилерди, көптүктөр (айкалышы, ордун которуусу, жылдырылышы жана элементтерин саноодо) жана алар менен катыштар (айталы, жеке тартипте); латын сөзүнөн combinare которгондо – бириктирүү, айкалышы деп түшүндүрөт. Комбинаторика математиканын башка чөйрөлөрү менен да байланышкан – алгебра, геометрия, ыктымалдуулук теориясы жана билимдин ар түрдүү чөйрөлөрүндө да колдонулат.

Жөнөкөй бир мисал карап көрөлү. Мейли, краска куюлган 4 челек бар: кызыл (К), сары (С), жашыл (Ж) жана күрөң (Кң), жана биз аларды коробкаларга ар биринде ар башка эки челектен кылып счалышыбыз керек болот. Биз аны төмөндөгүчө аткарсак болот:

Простой пример.gif
Простой пример.gif

Бизде алты ар түрдүү ыкма бар, эгерде бир коробкада сары жана кызыл болсо, анда ал кызыл жана сары челек краска менен бирдей болот. Бирок, эгерде бир түгөй түстөр менен белгилей турган болсок, анда он эки ыкма бар, анткени кызыл-сары түс менен сары-кызылдын айырмасы бар болот.

Простой пример 1.gif
Простой пример 1.gif
В начало

Комбинаториканын негизги формулалары

Правила сложения Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить m + n способами.

Пример 1. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?

Чыгарылышы: По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу сложения, можно осуществить 5 + 4 = 9 способами.

Ответ: 9 способов.

Пример 2. Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза?

Чыгарылышы: 1 способ: перебор вариантов. Для того, чтобы не пропустить и не повторить ни одно из чисел, будем записывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4, и, наконец, с цифры 7: 14, 17, 41, 47, 71, 74.

Ответ: 6 чисел.

2 способ: дерево возможных вариантов. Для этой задачи построена специальная схема. Ставим звездочку. Далее отводим от звездочки 3 отрезка. Так как в условии задачи даны 3 цифры – 1, 4, 7, то на концах отрезков ставим цифры 1, 4, 7. Далее от каждой цифры проводим по 2 отрезка. На концах этих отрезков записываем также цифры 1, 4, 7. Получились числа: 14, 17, 41 47, 71, 74. То есть всего получилось 6 чисел. Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола.

Пример 2 2 способ.gif
Пример 2 2 способ.gif

Правила умножения Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить m ∙ п способами.

Пример 3. Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза?

Чыгарылышы: Первую цифру двузначного числа можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать из оставшихся цифр уже двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 3∙2, т.е. 6.

Ответ: 6 чисел.

Факториал. Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n. Обозначение n!

0! = 1

1!=1

2! = 1∙ 2 = 2

3! = 1∙ 2 ∙ 3 = 6

4! = 1∙ 2 ∙ 3 ∙ 4 =24

5! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120

6! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720

7! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 = 5 040

8! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 = 40 320

9! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 ∙ 9 = 362 880

10! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 ∙ 9 ∙ 10 = 3 628 880

Свойства комбинаторики: перестановки, сочетание, размещение

Шахматная доска абстрация.jpg
Шахматная доска абстрация.jpg

Перестановкой называется конечное множество, в котором установлен порядок элементов. Число всевозможных перестановок из n элементов вычисляется по формуле: Pn = n!

Пример 4. Сколькими способами могут быть расставлены восемь участниц финального забега на восьми беговых дорожках?

Чыгарылышы. P8 = 8! = 40 320

Размещением Аkn из n элементов конечного множества по k, где k≤n, называют упорядоченное множество, состоящее из k элементов и вычисляется по формуле:

Формула размещения.png
Формула размещения.png

Пример 5.

Из 12 учащихся нужно отобрать по одному человеку для участия в городских олимпиадах по математике, физике, истории и географии. Каждый из учащихся участвует только в одной олимпиаде. Сколькими способами это можно сделать?

Решение.

Пример № 5.png
Пример № 5.png

Подмножества, составленные из n элементов данного множества и содержащие k элементов в каждом подмножестве, называют сочетаниями из n элементов по k. (Сочетания различаются только элементами, порядок их не важен: ab и ba – это одно и тоже сочетание) и вычисляется по формуле: .

Формула сочетаний.png
Формула сочетаний.png

Число размещений, перестановок и сочетаний связаны равенством: .

Число размещений, перестановок и сочетаний.png
Число размещений, перестановок и сочетаний.png

Различие между перестановками, размещениями, сочетаниями: В случае перестановок берутся все элементы и изменяется только их местоположение. В случае размещений берётся только часть элементов и важно расположение элементов друг относительно друга. В случае сочетаний берётся только часть элементов и не имеет значения расположение элементов друг относительно друга.

В начало

Ыктымалдуулук. Негизги түшүнүктөр

Ыктымалдуулук теориясында бир нече жолу кубулуштарды, тажрыйбаларды, эксперименттерди байкоо текшрүү (сыноо) деп аталат. Текшерүү (сыноонун) жыйынтыгын окуя деп айтабыз. Мисалы, экзамен тапшыруу- бул сыноо; аныкталган баа алуу – бул окуя, оюн кубикти ыргытуу же өкчөө – бул сыноо; тиги же бул тараы менен түшүү же упайдын саны – бул окуя.

Ыктумалдуулук – бул окуянын пайда болуш мүмкүндүгүн мүнөздөөчү сан. Ар бир мүмкүн болгон сыноонун жыйынтыкгы элементардык жыйынтык деп аталат.

Рнын ыктымалдуулугу А окуясынын ошол окуяга карата боло (ишке аша) турган сандын, баардык мүмкүн болгон элементардык жыйынтыкка дал келбеген жалпы топту түзүүчү катышы болот. Р ыктымалдуулук А окуясын Р = m/n , мында m- элементардык жыйынтык; n – сыноодогу баардык мүмкүн болгон элементардык жыйынтыгы, Анын ылайыктуу элементардык жыйынтыгын аныктоочу формула.

Маселе Алты бирдей жасалган корточкага К, Б, И, К, Е, Ш тамгалары жазылган. Карточкалар аралаштырылып кокустук боюнча бир катарга тизилет. Натыйжада БИШКЕК деп жазылып калгандай ыктымалдуулук эмнеге барабар болоорун тапкыла.

Задача Бишкек.gif
Задача Бишкек.gif

Чыгарылышы. Изделүүчү ыктымалдуулук Р = m/n , мында m- элементардык жыйынтык; n – сыноодогу баардык мүмкүн болгон элементардык жыйынтыгы формуласы менен эсептелинет.

Биздин учурда n = 6! = 720 (6 карточканын жайгаштырылыш саны);

m = 2 (бул сөздөгү “К” тамгасынын эки жолу кайталанышы, калгандары бирден эле жолу).

Тыянак, Р=2/720=1/360.

Задача «Волк, козел и капуста»

Крестьянину нужно перевезти через реку волка, козла и капусту. Лодка так мала, что в ней кроме крестьянина может поместиться только или волк, или козел, или капуста. Но если оставить волка с козлом, он его съест, а если оставить козла с капустой, то будет съедена капуста. Как быть крестьянину?

Для решения требуется расположить путем взаимной перестановки элементов и в соответствии с условием задачи в определенном порядке. Крестьянину следует начать переправу с перевозки козла. Затем он возвращается и берет волка, которого перевозит на другой берег и оставляет там, а козла возвращает назад на предыдущий берег. Оттуда забирает капусту и перевозит ее к волку. А затем возвращается и забирает козла.

Задача Волк коза капутса.gif
Задача Волк коза капутса.gif
В начало

Комбинаториканы колдонуу чөйрөсү

Комбинатордук маселелерди чыгаруу бирге дайыма керек болот. Мисалы, филологго канча тамгалардын айкалышын эске алуу керек болот? Үч ар түрдүү кездемеден модельер канча ар түрдүү кийимди ойлоп табууга болот? Сатып алуучу буюмдардын тизмесин, сабактардын жүргүртмөсүн, футболдук команданын, Рубик кубигин, тамакты даярдоодо, класста окуучуларды отургузуу, текчелерге китептерди жайгаштыруу, столду жасалгоолоодо кантип түзүү керек? Көпчүлүк балдар оюндары чучу кулак кармоо менен башталат. Карта менен, ширенке менен же ромашка менен төлгө ачуу дагы комбинаторикага негизделген. Крек болсо поэзия дагы комбинаториканы унутта калтырбайт! Ыр жана музыка, графика – живопись искусствосу – мунун баары комбинаторжук процесстер. Бекеринен бул чөйрөдөгү “компьютерлер” таң калаардыктай ийгиликтерге жетишпесе керек. Аягында, баардык адамдар – ДНК молекуларларындагы гендердин комбинациялары экенин айтса болот.

В начало

Комбинаторика программалоодо

Комбинаторика – бул ар кандай алгоритмдерди талдоодо, оптималдуу стратегияларды тандоодо керек болгон программисттердин чыныгы кенчи. Комбинатордук формулалар ыктымалдуулукту эсептөө үчүн, өзүнүн учурунда статистикалык гипотезаларды текшерүү үчүн керек болот. Программисттер комбинатордук маселелерди чыгарууда генерациялоо үчүн өзгөчө көңүлдү Generics Combinatorics программасы колдонгон пандигиталдык сандарга бурат.

Пандигиталдык сан деп, нөлдөн башталбаган жана бир сан кайра кайталанбаган сандарды айтабыз. Мисала 123456789.

Пандигиталдык сандары бар маселелерди логикалык сыяктуу эле керек болсо андан да жөнөкөй чыгарылат, анткени комбинатордук объектилер өзүнө сандарды камтыйт.

Число 123456789 — наименьшее пандигитальное число в десятичной системе счисления. При умножение на 8 результатом будет 987654312 — другое пандигитальное число, близкое к палиндрому исходного, за исключением двух последних цифр, обменявшихся местами. Это число также сохраняет свою пандигитальность при умножении:

- 2ге 123456789 ∙ 2 = 246913578,

- 4кө 123456789 ∙ 4 = 493827156,

- 5ке 123456789 ∙ 5 = 617283945,

- 7ге 123456789 ∙ 7 = 864197523.

Мисал катары башка санды санга 2, 4, 5, жана 7 (коэффициентке) көбөйтүүдө пандигиталдуулугун сактаган сан катары 1098765432 келтирсек болот. Эгерде 123456789ны 8ге жана 9га көбөйтсөк бул сандын толук палиндрому келип чыгат. Эгерде көбөйүүчүнү жана кошулуучуларды 1ге чоңойтсок, жыйынтыгы ондо экиге чейинки разраддагы 1 1диктен турган сан пайда болот.

Пандигитальные квадраты.gif
Пандигитальные квадраты.gif
В начало

Полезные ссылки

Вся наша жизнь состоит из множества разнообразных программ. Чтобы запустить ту или иную программу нужно ввести соответствующий верный пароль. В качестве кода в зависимости от рода программы могут выступать всевозможные цифры, слова или комбинации слов, поведение или действие. Комбинаторика используется в музыке, в мебельной деятельности, в различных играх (нарды, шашки, шахматы) и т.д. Читайте подробнее: [Электронный ресурс] // 2011-2017 Сила знаний URL: http://ya-znau.ru/znaniya/zn/80 (Дата посещения: 19.04.2018)

Толук чыгарылыштуу комбинатордук маселелерди төмөндө караса болот: [Электрондык ресурс] //mathprofi.ru, Александр Емелин, 2010-2018 URL: http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html (Катышуу датасы: 19.04.2018)

Необходимые теоретические сведения и формулы для решения комбинаторных задач школьного уровня можно посмотреть здесь: [Электронный ресурс] // Харламов А.В. элементы комбинаторики, 2016г. // URL: http://elibrary.sgu.ru/uch_lit/1626.pdf (Дата посещения: 21.04.2018)

Поиграем? Пусть имеется одна или несколько групп предметов. Играющие берут по очереди предметы из групп по правилам, которые заранее устанавливают: какое количество предметов разрешается брать за один раз и из скольких групп. Существует множество вариантов игры, и для большинства известна наилучшая стратегия, ведущая к выигрышу.:[Электронный ресурс] // ЮЦ «Восстание-6» URL: https://logic-games.spb.ru/nim/ (Дата посещения: 22.04.2018)

В начало

Глоссарий

Дискре́ттүүлү (лат. discretus — бөлүнгөн, үзгүлтүктүү) – үзгүлтүксүзгө карама-каршы коюлган, үзгүлтүктүү касиет. Дискреттүүлүк түшүнүгү: бин нече туруктуу абалдардын ортосундагы өзгөрүүчү бин нерсе, мисалы мүнөттүк жебечеси дискреттүү кыймылдаган механикалык сааты, 1/60га айлананын бөлүгү; өзүнчө бөлүктөрдү түзгөн, үзгүлтүктүү, бөлчөктүк бир нерсе.

Палиндро́м (грек. πάλιν — «артка, кайра» жана башка.-грек. δρóμος — «чуркоо, кыймыл»)— эки тарабынан бирдей окула турган сан, тамгалар айкалышы, сөз же текст.

Пандигиталдык сандар – бул нолдөн баштабаган жана бир сан кайра кайталанбаган сан.

Су́тра (санскр. सूत्र sūtra IAST, «жип», пали: sutta) — байыркы абадияттардагы лаконикалык жана үзгүлтүктүү айтылыш, афоризмдер, кийинчерээк – ушундай айтылыштардын. Сутраларда ар түрдүү билимдери, дээрлик Байыркы Индиянын диний-философиялык окуучлары жазылган.

В начало

Библиография

  • Комбинаторика: основные правила и формулы. : [Электронный ресурс] // 2011-2017 Сила знаний URL: http://ya-znau.ru/znaniya/zn/80 (Дата посещения: 19.04.2018)
  • Задачи по комбинаторике. Примеры решений.: [Электронный ресурс] //mathprofi.ru, Александр Емелин, 2010-2018 URL: *http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html (Дата посещения: 19.04.2018)
  • Сканворды, кроссворды и головоломки: [Электронный ресурс] // Пискунов Алексей © 2009-2018 http://www.graycell.ru/index.html (Дата посещения: 19.04.2018)
  • Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика: М.: ФИМА, МЦНМО, 2006. — 400 с.
  • Мир математики: в 40 т. Т.21: Ламберто Гарсия дель Сид. Замечательные числа. Ноль, 666, и другие бестии./Пер. с исп. –М.: Де Агостини, 2014. – 160 с.
В начало

Комбинаторика вокруг нас

Математика – жөнөкөй эрежелерге ылайык жана мааниге анча деле ээ эмес белгилөөлөрду колдонуу менен ойнолуучу жөн гана оюн. 

                     Давид Гильберт


Оюн ырахат жана кубаныч эле тартуулабастан, толук кандуу эс алуу менен кошо интеллектти машыктырууга үйрөтөт. Математиканын жетишкендиктерин колдонуу жаңы оюндардын теориясын андан ары өнүктүрүү үчүн жана жаңы машыктырууча маселелерди түзүүдө кзмат кылаарын ырахат менен ырастоого болот.

Кубик Рубика – это куб, как бы разрезанный на 27 одинаковых кубиков. В исходном положении каждая грань куба окрашена в один из 6 цветов. Остроумный механизм позволяет поворачивать любой слой из 9 кубиков, примыкающий к одной грани куба, вокруг ее центра. При этом цвета граней смешиваются. Задача состоит в том, чтобы вернуть разноцветные грани кубика в исходное положение. Теоретически из любого состояния кубика можно вернуться в исходное, не более чем за 23 хода.

Лучшее время, показанное на чемпионате мира 1982 г. по скоростной сборке кубика Рубика, составило всего 22,95 секунды. А в наше время дети собирают за считанные секунды. Давайте убедимся

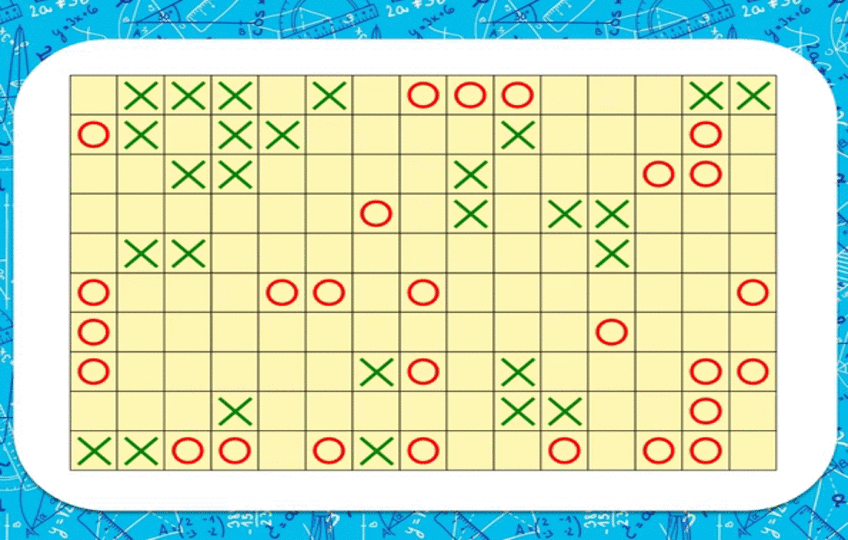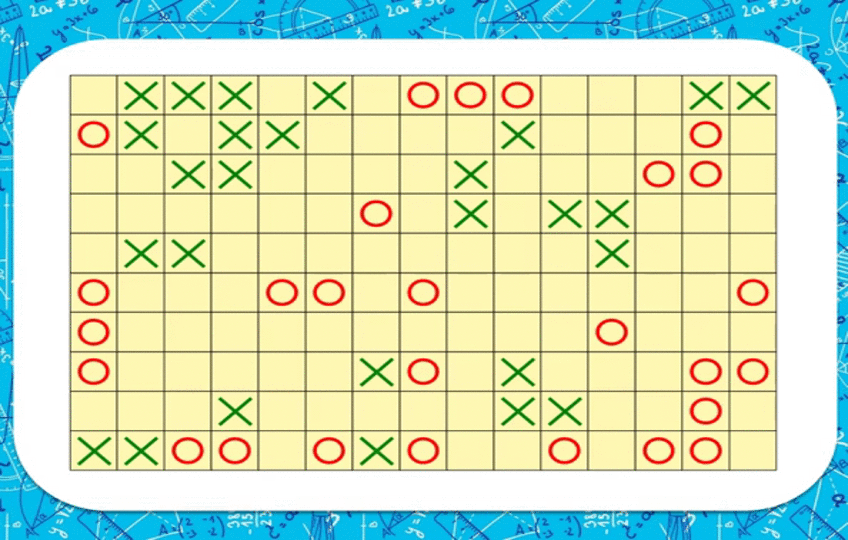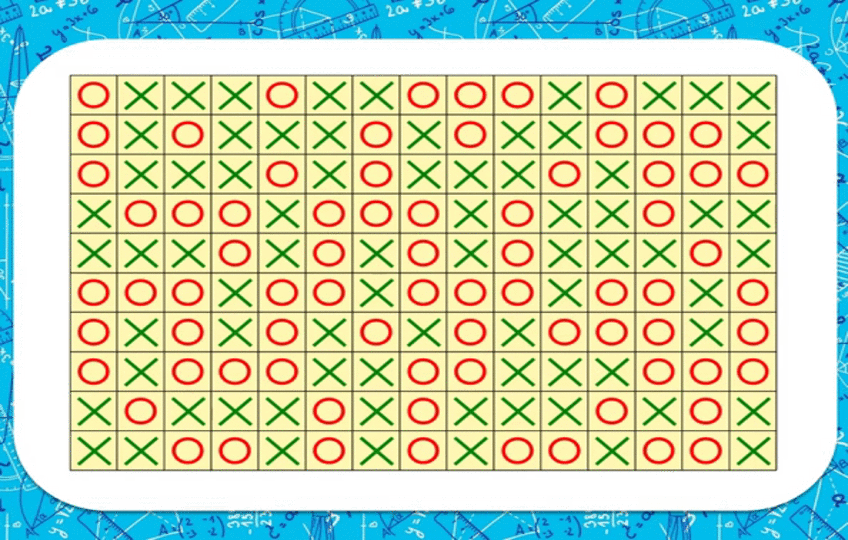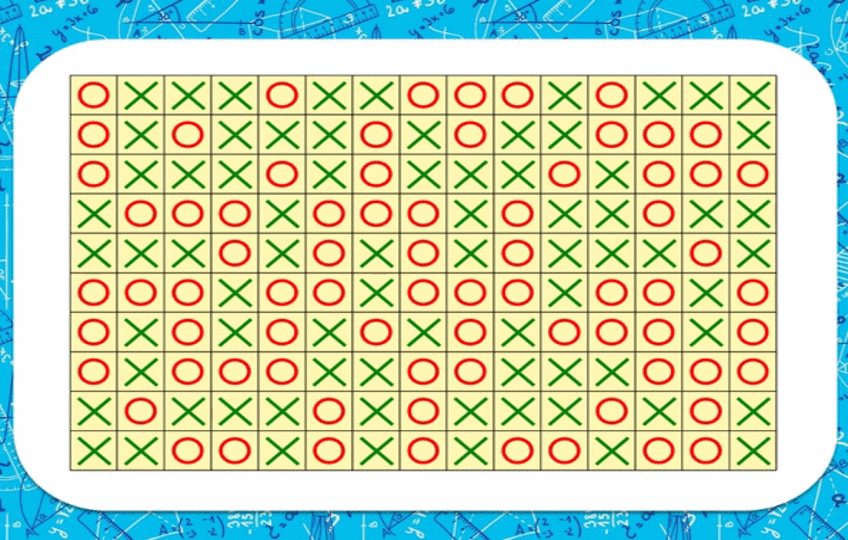
Жебечелер

Ар бир клеткадагы сандардан алардын саны алгачкы санга тең болуп, мында торчодогу сан эсепке алынбагандай кылып жебечелерди жүргүзүү керек. Жебечелер тигинен жана туурасынан жүргүзүлүшү керек. Жебечелер баардык бош клеткаларда болушу керек.

Стрелочки.gif

Судоку

1ден 9га чейинки сандардын бош торчосунда ар бир сапчадагы, ар бир мамычадагы жана ар бир квадраттагы сандар бирден гана жолу кездешкендей жайгаштыруу керек.

Судоку .gif

Лесенка

Пирамиданын чокусунан негизине чейинки сандары ар башка болгондой жолду табуу керек.

Лесенка.gif

Пирамида

Уячалардын 1ден 9га чейин төмөнкү эрежеге ылайык толтуруу керек: уячадагы сан төмөнкү эки уячадагы сандардын суммасы же айырмасы катары болуп, пиармиданын ар бир сабындагы сандар кайталнбашы керек.

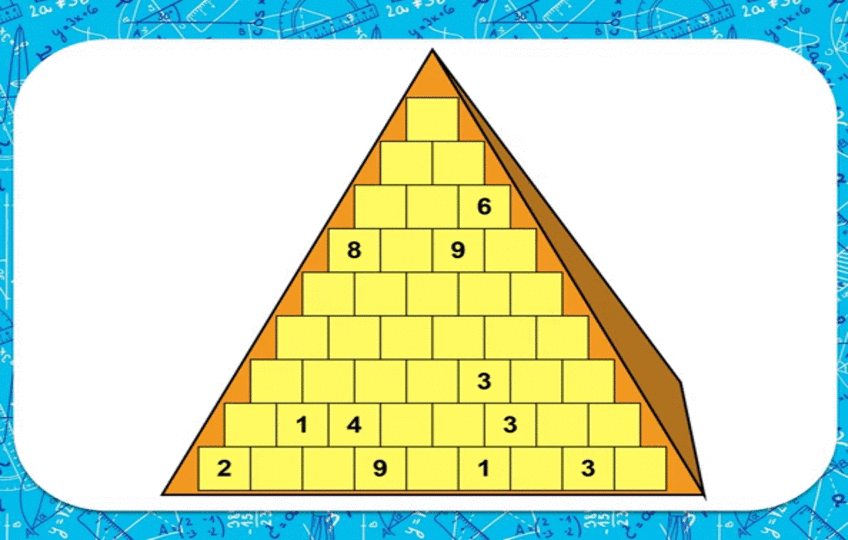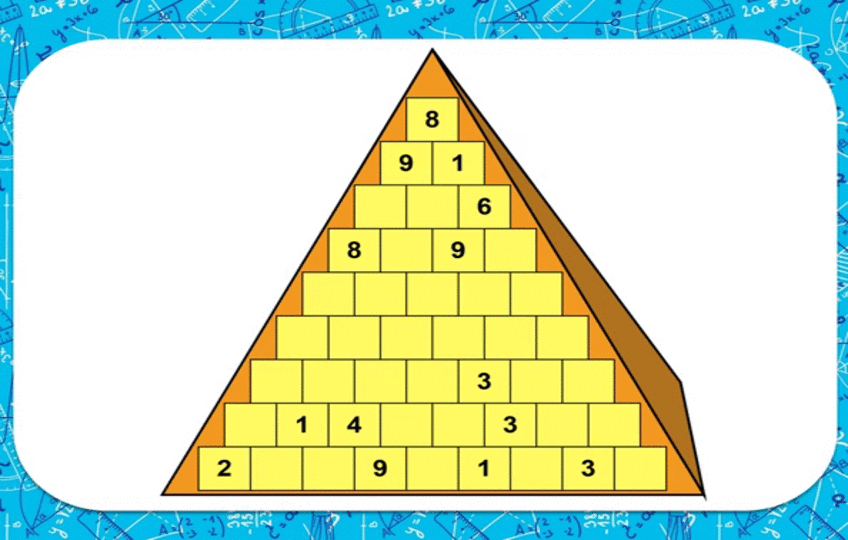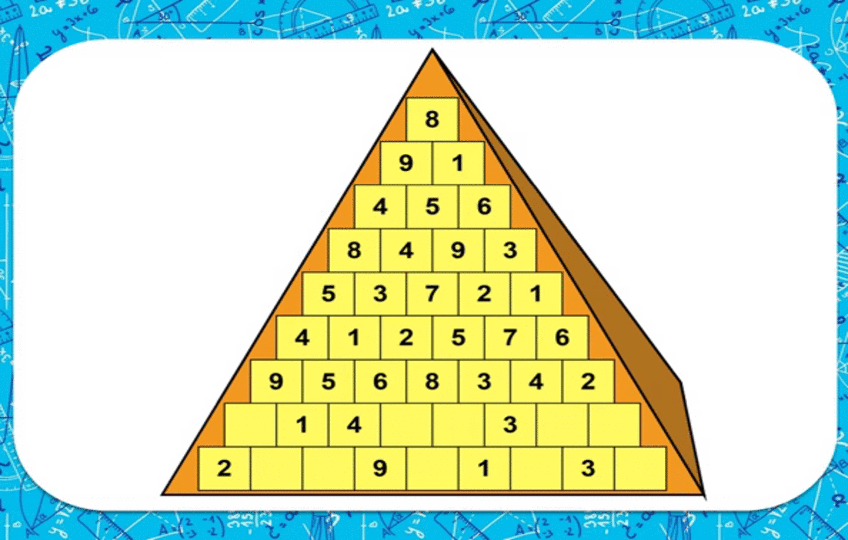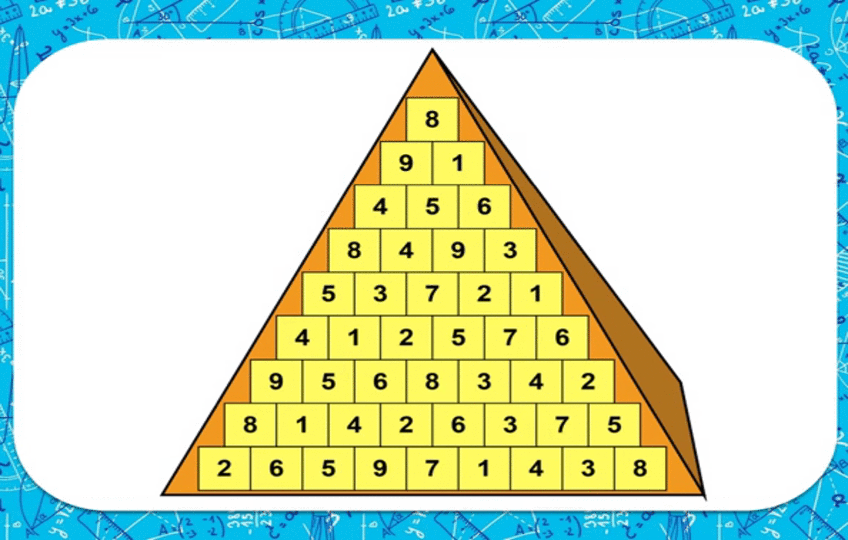
Пирамида.gif

Крестики-нолики Самая известная древняя игра. В квадрате, разделенном на девять клеток, игроки по очереди ставят в свободную клетку свой знак: крестик или нолик, стараясь выстроить три крестика или три нолика подряд. Тот, кто первым сделает это, тот и выигрывает.

Если не делать ошибок, то игра оканчивается в ничью. Выиграть можно только в том случае, если противник ошибется. Самый правильный ход –занять угловую клетку. И если партнер не ответит на это своим знаком в центре, то он проиграл.

Крестики нолики.gif
Ребусы
  • Ребус № 1 .png
  • Ребус № 2.png
  • Ребус № 3 Комбинаторика.png
  • Ребус № 4 .png
  • Ребус № 5 .png

Ответы:

  1. Вариант
  2. Сочетания
  3. Факториал
  4. Событие
  5. Исход
Источник — «https://bb.edu.gov.kg/index.php?title=KR:Математика:_Комбинаториканын_негиздери&oldid=15994»