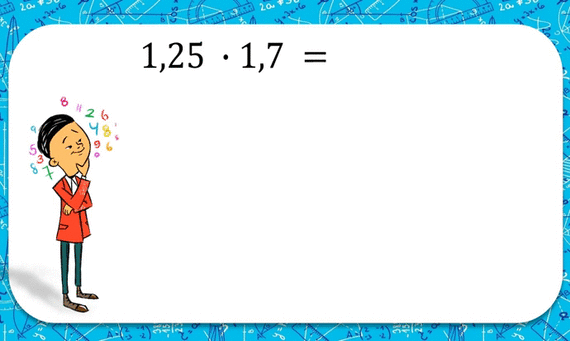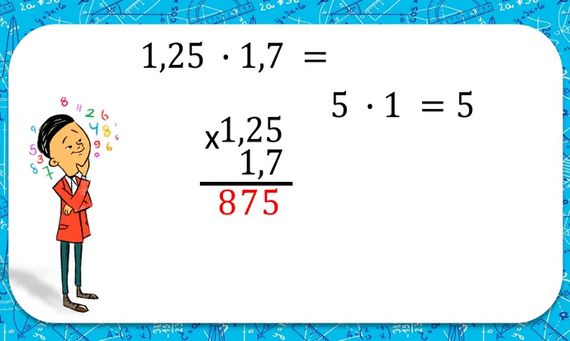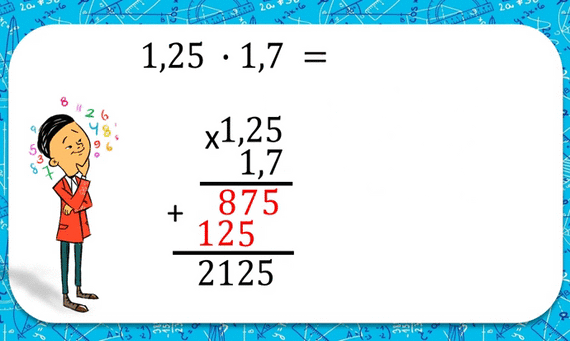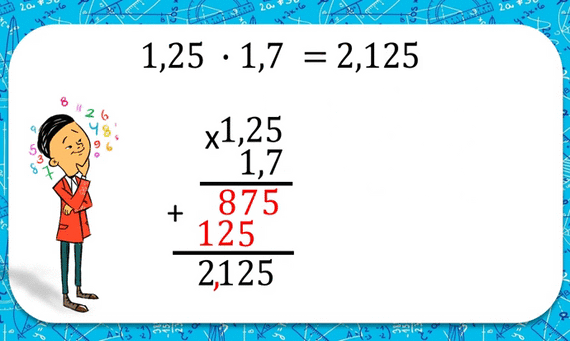Математика: Ондук бөлчөктөрдөгү арифметикалык амалдар — различия между версиями
Azim (обсуждение | вклад) (→Глоссарий) |
Admine2 (обсуждение | вклад) |
||
| (не показано 5 промежуточных версий 3 участников) | |||
| Строка 4: | Строка 4: | ||
Жөнөкөй бөлчөктү эсептөөдө анын бөлүмү канчалык чоң болсо ошончолук ири көлөмдө болот. Башкы кыйынчылык бөлчөктү бирдей бөлүмгө келтирип алууда; ал болсо бөлүмдүн каалагандай сан болушунан жана аны тандоодо эч кандай системанын жоктугунда. Ошондуктан байыртан эле аны каалагандай тандабастан, систематикалык бирдиктин бөлүгү жөнөкөй бөлчөктө бөлүмдүн ролун ойнойт деген ойго келишкен. | Жөнөкөй бөлчөктү эсептөөдө анын бөлүмү канчалык чоң болсо ошончолук ири көлөмдө болот. Башкы кыйынчылык бөлчөктү бирдей бөлүмгө келтирип алууда; ал болсо бөлүмдүн каалагандай сан болушунан жана аны тандоодо эч кандай системанын жоктугунда. Ошондуктан байыртан эле аны каалагандай тандабастан, систематикалык бирдиктин бөлүгү жөнөкөй бөлчөктө бөлүмдүн ролун ойнойт деген ойго келишкен. | ||
| − | + | {{TimelineKG}} | |
==Ондук бөлчөктөрдүн артыкчылыгы== | ==Ондук бөлчөктөрдүн артыкчылыгы== | ||
| Строка 15: | Строка 15: | ||
Арифметикада кандай аткарылаарын карап көрөлү: | Арифметикада кандай аткарылаарын карап көрөлү: | ||
| − | <div class=”show-for-large-up”>{{center|[[Файл: | + | <div class=”show-for-large-up”>{{center|[[Файл:Slojen_10_drob.gif|500px]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Slojen_10_drob.gif|500px]]}}</div> |
'''Ондук бөлчөктөрдү кошууда жана алууда''' мындай кылышат: | '''Ондук бөлчөктөрдү кошууда жана алууда''' мындай кылышат: | ||
| − | 1. эгер керек болсо үтүрдөн кийинки сандардын санын оң жагына нөл кошуу менен ондук бөлчөктүн негизги касиетине таяп бирдей кылынат, ал болсо бөлчөктүн көлөмүнө | + | 1. эгер керек болсо үтүрдөн кийинки сандардын санын оң жагына нөл кошуу менен ондук бөлчөктүн негизги касиетине таяп бирдей кылынат, ал болсо бөлчөктүн көлөмүнө таасирин тийгизбейт. |
2. Бөлчөктөрдү алардын үтүрлөрү биринин астына бири дал келгендей кылып жазышат (разряддын астына разряд болгондой кылып) | 2. Бөлчөктөрдү алардын үтүрлөрү биринин астына бири дал келгендей кылып жазышат (разряддын астына разряд болгондой кылып) | ||
| Строка 31: | Строка 31: | ||
'''Ондук бөлчөктөрдү көбөйтүү''' | '''Ондук бөлчөктөрдү көбөйтүү''' | ||
| − | <div class=”show-for-large-up”>{{right|[[Файл: | + | <div class=”show-for-large-up”>{{right|[[Файл:Umnoj_drob_kyrg.gif|500px]]}}</div> |
| − | <div class="hide-for-large-up">{{right|[[Файл: | + | <div class="hide-for-large-up">{{right|[[Файл:Umnoj_drob_kyrg.gif|500px]]}}</div> |
| − | Бир ондук санды экинчисине көбөйтүүдө , аларды бүтүн сан сыяктуу көбөйтүп алыш керек, андан кийин алынган санды оң жагынан ондук белгилерине карата бөлүп алабыз анда эки көбөйтүлгөндү тең алабыз.Сүрөттү карап көбөйтүүдө мамыча түрүндө кандай туура жазылаарына көңүл бөл. | + | Бир ондук санды экинчисине көбөйтүүдө, аларды бүтүн сан сыяктуу көбөйтүп алыш керек, андан кийин алынган санды оң жагынан ондук белгилерине карата бөлүп алабыз анда эки көбөйтүлгөндү тең алабыз.Сүрөттү карап көбөйтүүдө мамыча түрүндө кандай туура жазылаарына көңүл бөл. |
| Строка 44: | Строка 44: | ||
'''Ондук бөлчөктөрдү бөлүү''' | '''Ондук бөлчөктөрдү бөлүү''' | ||
| − | <div class=”show-for-large-up”>{{right|[[Файл: | + | <div class=”show-for-large-up”>{{right|[[Файл:delen_drob.gif|500px]]}}</div> |
| − | <div class="hide-for-large-up">{{right|[[Файл: | + | <div class="hide-for-large-up">{{right|[[Файл:delen_drob.gif|500px]]}}</div> |
Ондук бөлчөктү натуралдык сандарга бөлүү үчүн кийинки алгоритмдерди эске алуу керек: | Ондук бөлчөктү натуралдык сандарга бөлүү үчүн кийинки алгоритмдерди эске алуу керек: | ||
Ондук бөлчөктү натуралдык санга мамыча түрүнүн эрежеси боюнча үтүргө маани бербей туруп бөлүү. Алынган жекеге үтүрдү коёбуз, качан бөлүнүүчүнүн бүтүн бөлүгүн бүткөндөн кийин. Эгерде бөлүнүүчүнүн бүтүн бөлүгү бөлүнүүчүдөн кичине болсо анда жекеге 0 бүтүн беребиз. Сүрөттө “бурчтук” бөлүүнүн жазуусу көрсөтүлгөн. | Ондук бөлчөктү натуралдык санга мамыча түрүнүн эрежеси боюнча үтүргө маани бербей туруп бөлүү. Алынган жекеге үтүрдү коёбуз, качан бөлүнүүчүнүн бүтүн бөлүгүн бүткөндөн кийин. Эгерде бөлүнүүчүнүн бүтүн бөлүгү бөлүнүүчүдөн кичине болсо анда жекеге 0 бүтүн беребиз. Сүрөттө “бурчтук” бөлүүнүн жазуусу көрсөтүлгөн. | ||
| Строка 57: | Строка 57: | ||
Жогорудагы айтылгандардан кийин биз ондук бөлчөктү- бул кадимки эле сандар деп айта алабыз. Биз аларды кошуп, биринен бирин алып, көбөйтүп жана бөлө алабыз. Алар менен математикалык амалдарды туура кылуу эң башкы нерсе, анткени кетирилген арифметикалык катадан силердин ийгилигинер көз каранды. Силер бул нерселерди кантип кылышты билээриңерге талаш жок, ошондой болсо дагы бөлчөктөр менен иштей турган амалдардын ылайыгы үчүн силерге ондук бөлчөктөрдүн негизги касиетин эстеп калууну сунуштайбыз. Алар абдан жөнөкөй, биз аларды бир кичинекей эскертмеге чогулттук. Жүктөгүлө, чыгарып алгыла жана пайдалангыла! | Жогорудагы айтылгандардан кийин биз ондук бөлчөктү- бул кадимки эле сандар деп айта алабыз. Биз аларды кошуп, биринен бирин алып, көбөйтүп жана бөлө алабыз. Алар менен математикалык амалдарды туура кылуу эң башкы нерсе, анткени кетирилген арифметикалык катадан силердин ийгилигинер көз каранды. Силер бул нерселерди кантип кылышты билээриңерге талаш жок, ошондой болсо дагы бөлчөктөр менен иштей турган амалдардын ылайыгы үчүн силерге ондук бөлчөктөрдүн негизги касиетин эстеп калууну сунуштайбыз. Алар абдан жөнөкөй, биз аларды бир кичинекей эскертмеге чогулттук. Жүктөгүлө, чыгарып алгыла жана пайдалангыла! | ||
| − | <div class=”show-for-large-up”>{{center|[[Файл: | + | <div class=”show-for-large-up”>{{center|[[Файл:Pravila_drob_kyrg.jpg|800px]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Pravila_drob_kyrg.jpg|800px]]}}</div> |
<div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | ||
| Строка 65: | Строка 65: | ||
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | <ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | ||
<li class="active"> | <li class="active"> | ||
| − | [[file:Пример 1 кт.gif | + | [[file:Пример 1 кт.gif]] |
</li> | </li> | ||
<li> | <li> | ||
| − | [[file:Пример_2_кт.gif | + | [[file:Пример_2_кт.gif]] |
</li> | </li> | ||
<li> | <li> | ||
| − | [[file:Примеры_десятичные_дроби_3_кт.gif | + | [[file:Примеры_десятичные_дроби_3_кт.gif]] |
</li> | </li> | ||
</ul> | </ul> | ||
| Строка 85: | Строка 85: | ||
==Пайдалуу шилтемелер== | ==Пайдалуу шилтемелер== | ||
| − | Ондук бөлчөктүн арасынан эң көп колдонулган бөлчөк бул- 0,01, ал процент (пайыз) деп аталат жана 1% деп белгиленет. Пайыздык эсепти түшүнүү жана чыгара билүү ар бирибиз үчүн эң керек. Пайыздар адамдын жашоосундагы баардык тарапта кездешет. Бул түшүнүксүз Бухгалтерияны, финансыны статистиканы карай албайбыз. Жумушчуга айлык эсептеп | + | Ондук бөлчөктүн арасынан эң көп колдонулган бөлчөк бул- 0,01, ал процент (пайыз) деп аталат жана 1% деп белгиленет. Пайыздык эсепти түшүнүү жана чыгара билүү ар бирибиз үчүн эң керек. Пайыздар адамдын жашоосундагы баардык тарапта кездешет. Бул түшүнүксүз Бухгалтерияны, финансыны статистиканы карай албайбыз. Жумушчуга айлык эсептеп берүү үчүн налогго которулуучу пайыздарды билиш керек; сактык банкынан счет ачыш үчүн же кредит алуу үчүн биз биринчи суммага төлөнүүчү пайызын көлөмүнө кызыгабыз. Ал эми соодада “пайыз” деген түшүнүк абдан көп колдонулат. Биз ар дайым арзандатып сатуу, арзандатуу, пайда ж.б.- мунун баары пайыздар. Азыркы жашап жаткан адамга маалыматтын чоң агымында жакшы аралашып, жашоонун ар кандай абалдарында туура чечим кабыл ала билиши зарыл. Бул үчүн пайыздык эсепти жакшы чыгаруу керек. Мындай эсептерди, маселелерди кандай чыгарыш керектигин кененирээк билгиңер келсе бул жерден карагыла: Проценттерге маселе: [Электрондук ресурс] // «Сёзнайка.ру», 2015. URL: http://www.seznaika.ru/matematika/ege/114-2009-12-06-18-08-29 (кайрылуу датасы: 20. 11. 2017) |
Комикс – бул күчтүү айтылган. Дүйнөгө белгилүү карикатурист Ларри Гониканын жаңы китеби, ал Гарвар Университетинде математиканы алгебранын мектеп программасынын негизги темаларын камтыган интенсивдик курсунда окуйт жана окутат. Автор тирүү юморду алгебранын тарыхына экскурсия кылган жана “илимдердин ханышасынын” азыркы турмушубуздагы колдонулушуна көптөгөн мисалдарды келтирген. Гониктин татаал материалды кызыктуу, тамашалуу, жана жеңил кабыл ала тургандай кылып тартуулоодогу уникалдуу шыгы, ошондой эле кемчиликсиз таза түзүлүшү бул китепти мектеп окуучулары үчүн баардык каалагандар үчүн, өзүнүн математикалык шыгын формада кармагысы келгендер үчүн дагы эң сонун окуу куралы болуп саналат.: Алгебра. Табигый илим комикстерде. Ларри Гоник.: [Электрондукресурс] //Братчикова Надежда Владимировна, 2016-2017. URL:http://mathlife.ru/algebra . (кайрылуу датасы: 20. 11. 2017) | Комикс – бул күчтүү айтылган. Дүйнөгө белгилүү карикатурист Ларри Гониканын жаңы китеби, ал Гарвар Университетинде математиканы алгебранын мектеп программасынын негизги темаларын камтыган интенсивдик курсунда окуйт жана окутат. Автор тирүү юморду алгебранын тарыхына экскурсия кылган жана “илимдердин ханышасынын” азыркы турмушубуздагы колдонулушуна көптөгөн мисалдарды келтирген. Гониктин татаал материалды кызыктуу, тамашалуу, жана жеңил кабыл ала тургандай кылып тартуулоодогу уникалдуу шыгы, ошондой эле кемчиликсиз таза түзүлүшү бул китепти мектеп окуучулары үчүн баардык каалагандар үчүн, өзүнүн математикалык шыгын формада кармагысы келгендер үчүн дагы эң сонун окуу куралы болуп саналат.: Алгебра. Табигый илим комикстерде. Ларри Гоник.: [Электрондукресурс] //Братчикова Надежда Владимировна, 2016-2017. URL:http://mathlife.ru/algebra . (кайрылуу датасы: 20. 11. 2017) | ||
| Строка 113: | Строка 113: | ||
Биздин эранын III кылымында ондук бөлчөктөр Кытайда салмак менен көлөмдү эсептөөдө колдонула баштады. Акырындап алар математикага тереңирээк сүңгүп кире баштаган. Ал эми Европада ондук бөлчөктөр алда канча кеч колдолуна баштаган. | Биздин эранын III кылымында ондук бөлчөктөр Кытайда салмак менен көлөмдү эсептөөдө колдонула баштады. Акырындап алар математикага тереңирээк сүңгүп кире баштаган. Ал эми Европада ондук бөлчөктөр алда канча кеч колдолуна баштаган. | ||
| − | Бирок кытайлыктардан | + | Бирок кытайлыктардан көз карандысыз ондук бөлчөктөрдү байыркы Самарканд шаарынан астроном аль-Каши ачкан. Ал ХV кылымда жашап жана эмгектенген. Ал өзүнүн теориясын “арифметикага ачкыч” деген трактатында берген, ал 1427 жылы жарыкка чыккан. Аль-Каши бөлчөктөрдүн жаңы формада жазылышын колдонууну сунуштаган. Эми бүтүн дагы бөлчөктүү бөлүгү бир катарда жазылат. Аларды бөлүүдө самарканддык окумуштуу үтүрдү пайдаланган эмес. Ал бүтүн санды жана бөлчөктүү бөлүгүн кызыл жана кара сыяны колдонуу менен жазган. Кээде Аль-Каши аларды бөлүү үчүн вертикалдык сызыкты дагы пайдаланган. |
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | <ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | ||
| Строка 126: | Строка 126: | ||
Бөлчөктүн жаңы түрлөрү Европалык математиктердин эмгектеринде XIII кылымдан баштап пайда боло баштаган. Бирок алар аль-Кашинин эмгектерин жана кытайлыктардын тапкандарын билишкен эмес экендигин айтып коюшубуз керек. Ондук бөлчөктөр Иордан Неморариянын эмгектеринде дагы пайда болгон. Андан кийин XVI кылымда француз окумуштуусу “Математикалык канонду” жазган, анда тригонометриялык таблица камтылган. Алардан Виет ондук бөлчөктөрдү алган. Бүтүн жана бөлчөк жагын айырмалаш үчүн окумуштуу вертикалдык сызыкчаны жана ар кандай көлөмдөгү шрифтерди пайдаланган. Бирок булар илимдеги кээ бир гана жекече окуялар болгон. | Бөлчөктүн жаңы түрлөрү Европалык математиктердин эмгектеринде XIII кылымдан баштап пайда боло баштаган. Бирок алар аль-Кашинин эмгектерин жана кытайлыктардын тапкандарын билишкен эмес экендигин айтып коюшубуз керек. Ондук бөлчөктөр Иордан Неморариянын эмгектеринде дагы пайда болгон. Андан кийин XVI кылымда француз окумуштуусу “Математикалык канонду” жазган, анда тригонометриялык таблица камтылган. Алардан Виет ондук бөлчөктөрдү алган. Бүтүн жана бөлчөк жагын айырмалаш үчүн окумуштуу вертикалдык сызыкчаны жана ар кандай көлөмдөгү шрифтерди пайдаланган. Бирок булар илимдеги кээ бир гана жекече окуялар болгон. | ||
{{center|[[Файл:Титульный_лист_издания_Десятой_Симона_Стевина.jpg]]}} | {{center|[[Файл:Титульный_лист_издания_Десятой_Симона_Стевина.jpg]]}} | ||
| − | Европада ондук бөлчөктөрдүн күнүмдүк маселелерин чечүү кичине кечирээк башталган. Бул болсо XVI кылымдын аягында голландиялык окумуштуу Симон Стевиндин эмгеги болгон. Ал 1585 жылы “Онунчу” деп аталган математикалык эмгегин чыгарган. Анда окумуштуу ондук бөлчөктөрдүн арифметикада, акча системасында жана көлөм менен ченди аныктоодо колдонуу теориясын айткан. | + | Европада ондук бөлчөктөрдүн күнүмдүк маселелерин чечүү кичине кечирээк башталган. Бул болсо XVI кылымдын аягында голландиялык окумуштуу Симон Стевиндин эмгеги болгон. Ал 1585-жылы “Онунчу” деп аталган математикалык эмгегин чыгарган. Анда окумуштуу ондук бөлчөктөрдүн арифметикада, акча системасында жана көлөм менен ченди аныктоодо колдонуу теориясын айткан. |
{{center|[[Файл:Франсуа_Виет_Опера_Математике.jpg]]}} | {{center|[[Файл:Франсуа_Виет_Опера_Математике.jpg]]}} | ||
| − | Стевин ошондой эле үтүрдү колдонгон эмес.Ал түшүнүктүү болуш үчүн ар бир сандын үстүнө ( же сандан кийин) ал сандын разрядынын номерин айланага койгон. | + | Стевин ошондой эле үтүрдү колдонгон эмес. Ал түшүнүктүү болуш үчүн ар бир сандын үстүнө ( же сандан кийин) ал сандын разрядынын номерин айланага койгон. |
| − | Биринчи жолу үтүр ондук бөлчөктү 1592 жылы эки бөлүккө бөлгөн. Бирок | + | Биринчи жолу үтүр ондук бөлчөктү 1592-жылы эки бөлүккө бөлгөн. Бирок Англияда үтүрдүн оордуна чекитти пайдаланышкан. Америка кошмо штаттарында азыркыга чейин ондук бөлчөктү ушундай чекит менен жазышат. Мындай бүтүн жана бөлчөктү бөлүп жазууда эки белгини тең пайдалана берүүнү алгачкылардын бири болуп шотландык математик Джон Непер сунуштаган. Ал өз оюн 1617-жылы айткан. Үтүрдү немец окумуштуусу Иоганн Кеплер дагы пайдаланган. |
{{center|[[Файл:Ондук_бөлчөктөрдү_ар_кандай_белгилөө.jpg]]}} | {{center|[[Файл:Ондук_бөлчөктөрдү_ар_кандай_белгилөө.jpg]]}} | ||
| − | Бөлчөктөр жөнүндө толук теория азыркыдан аз гана айырмаланган, ал 1701 жылы жазылган арифметика бонча биринчи китепте Леонтий Филиппович Магницкий тарабынан берилген. “Арифметика” бир нече бөлүктөн турган. Бөлчөктөр туураалуу автор кененирээк “Сынык жана бөлүнгөн сандар жөнүндө” деген бөлүмүндө айтып берген. Магницкий сынган сандар менен амалдарды жүргүзүп, аларды ар кандай белгилеген.</p> | + | Бөлчөктөр жөнүндө толук теория азыркыдан аз гана айырмаланган, ал 1701-жылы жазылган арифметика бонча биринчи китепте Леонтий Филиппович Магницкий тарабынан берилген. “Арифметика” бир нече бөлүктөн турган. Бөлчөктөр туураалуу автор кененирээк “Сынык жана бөлүнгөн сандар жөнүндө” деген бөлүмүндө айтып берген. Магницкий сынган сандар менен амалдарды жүргүзүп, аларды ар кандай белгилеген.</p> |
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | <ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | ||
<li class="active"> | <li class="active"> | ||
| Строка 161: | Строка 161: | ||
{{center|[[Файл:Деление и умножение десятичных дробей кт.jpg]]}} | {{center|[[Файл:Деление и умножение десятичных дробей кт.jpg]]}} | ||
| + | </div> | ||
| + | <div class="sbstyle"> | ||
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Тестти өтүңүз</div> | ||
| + | </div> | ||
| + | |||
</div> | </div> | ||
</div> | </div> | ||
</div> | </div> | ||
{{lang|Математика: Арифметические действия над десятичными дробями}} | {{lang|Математика: Арифметические действия над десятичными дробями}} | ||
Текущая версия на 08:54, 22 октября 2018
Жөнөкөй бөлчөктү эсептөөдө анын бөлүмү канчалык чоң болсо ошончолук ири көлөмдө болот. Башкы кыйынчылык бөлчөктү бирдей бөлүмгө келтирип алууда; ал болсо бөлүмдүн каалагандай сан болушунан жана аны тандоодо эч кандай системанын жоктугунда. Ошондуктан байыртан эле аны каалагандай тандабастан, систематикалык бирдиктин бөлүгү жөнөкөй бөлчөктө бөлүмдүн ролун ойнойт деген ойго келишкен.
-

Лю Хуэй
Лю Хуэй – кытай математига. Үчпадышачылык доорунда гы Вэй падышачылыгында жашаган. «Математика тогуз китебинде» (Цзю чжан суаньшу) деп аталган эмгегинде күнүмдүк жашоодогу математикалык маселелердин чыгарылышынын жыйнагын көрсөткөн комментарийлери менен белгилүү. Лю Хуэй 263–жылы өзүнүн комментарийлери кошулган «Цзю чжан суаньшу» эмгегин жарыялаган, бул китеп жарыяланган бүгүнкү күнгө чейинки сакталган байыркы китептерден.
-

Чун – Чжи
Чун – Чжи (429—500) — кытай окумуштуусу жана математиги.
Бирден бир белгилүү кытай окумуштуусу, математиги, астроному, инженери, механик жана адабиятчысы. Дүйнөдө биринчилерден болуп π санын үтүрдөн кийин жети белги тактыкка чейин эсептеген, ага 3,1415926 жана 3,1415927 ортосундагы тагыраак маанини миң жыл өткөндөн кийин беришкен.
-
Аль-Бируни
Ортокылымдагы персиялык окумуштуу–энциклопедисти жана ойчулу, тарых, география, филология, астрономия, математика, механика, геодезия, минералогия, фармакология, геология ж.б. боюнча капиталдык эмгектердин автору. Бируни өзүнүн доорунун баардык илимдерин билген. Математикага көп көңүл бурган, өзгөчө тригонометрияга: «Канона Мас‘уда» белгилүү бөлүгүнөн сырткары ал «Тегеректеги ички сынык сызыгынын жардамы менен хорданы аныктоо жөнүндө» жазмасына арнаган.
-

Аль – Каши
XV кылымдын ири математиктеринин жана астрономдорунун бири, Самарканд обсерваториясынын жетекчилеринин бири. Ондук бөлчөктүн теориясынын биринчи систематикалык баяндамасын, π санынын чоңдугун үтүрдөн кийин 16 белгиге чейин даана эсептелишин жарыялаган.
-

Франсуа Виет
Франсуа Виет, сеньор де ля Биготьер – Француз математиги. Элементардык алгебранын дээрлик бардыгын иштеп чыккан. Алгебралык теңдемедеги тамыр менен коэффициенттин ортосундагы көз карандылыкты берген «Виеттин формуласы» белгилүү. Виет аты кийинки математикалык объектилерди алып жүрөт: Виеттин тригонометриялык формуласы Виеттин формуласы.
-

Христофор Клавий
Христофор Клавий – герман математиги жана астроному. 1574–жылы ал Евклиддин «Башталышын» чыгарган жана ага комментарий берген, а 1608–жылы алгебра боюнча китеп жазган.
Бөлчөктөрдүн теориясын жана алар менен болгон амалдарды бүтүн жазган.
-

Джованни Антонио Маджини
Джованни Антонио Маджини – италиялык картограф, астроном жана математик.
Маджини биринчилерден ондук бөлчөктүн бүтүн бөлүнүнөн бөлчөк бөлүгүн ажыратуу үчүн үтүр белгисин сунуштаган. Окумуштуунун урматына ай кратери деп Айдын берики бетин аташкан.
-

Джон Непер
Джон Непер – шотландия математик, логарифманы алгачкылардан болуп ойлоп тапкан, логарифмалык жадыбалды биринчилерден ойлоп тапкан астроном. 1614–жылы Непер Эденбургда «Логарифманын таң калаарлык жадыбалы» аттуу чыгармасын жарыялаган. Анын эмгектеринен ондук чекиттерди бөлчөк бөлүктү бүтүн бөлүгүнөн бөлүүдө системалуу колдонгонун көрүүгө болот.
-

Симон Стевин
Симон Стевин – фламанддык математик, механик жана инженер. Соода иштери боюнча көп саякаттаган, кийин принц Морица Оранскийдин өздүк кеңешчиси болгон. Стевиндин «Онунчу» трактаты арифметикалык ондук бөлчөктүн практикалык сүрөттөлүшүн, ошондой эле аларды колдонуудагы дилгерлүү жана жакшы аргументтелген пропогандасы, атап айтканда, ченөө системасы жана тыйындар иштери камтылган.
-

Иоганн Кеплер
Иоганн Кеплер – немис математиги, астроном, механик, оптик. Ар кандай айлануу телолордун көлөмдөрүн табуу ыкмаларын интегралдык эсептөөлөрдү колдонуу аркылуу тапкан. Орточо арифметикалык терминин киргизген.
-
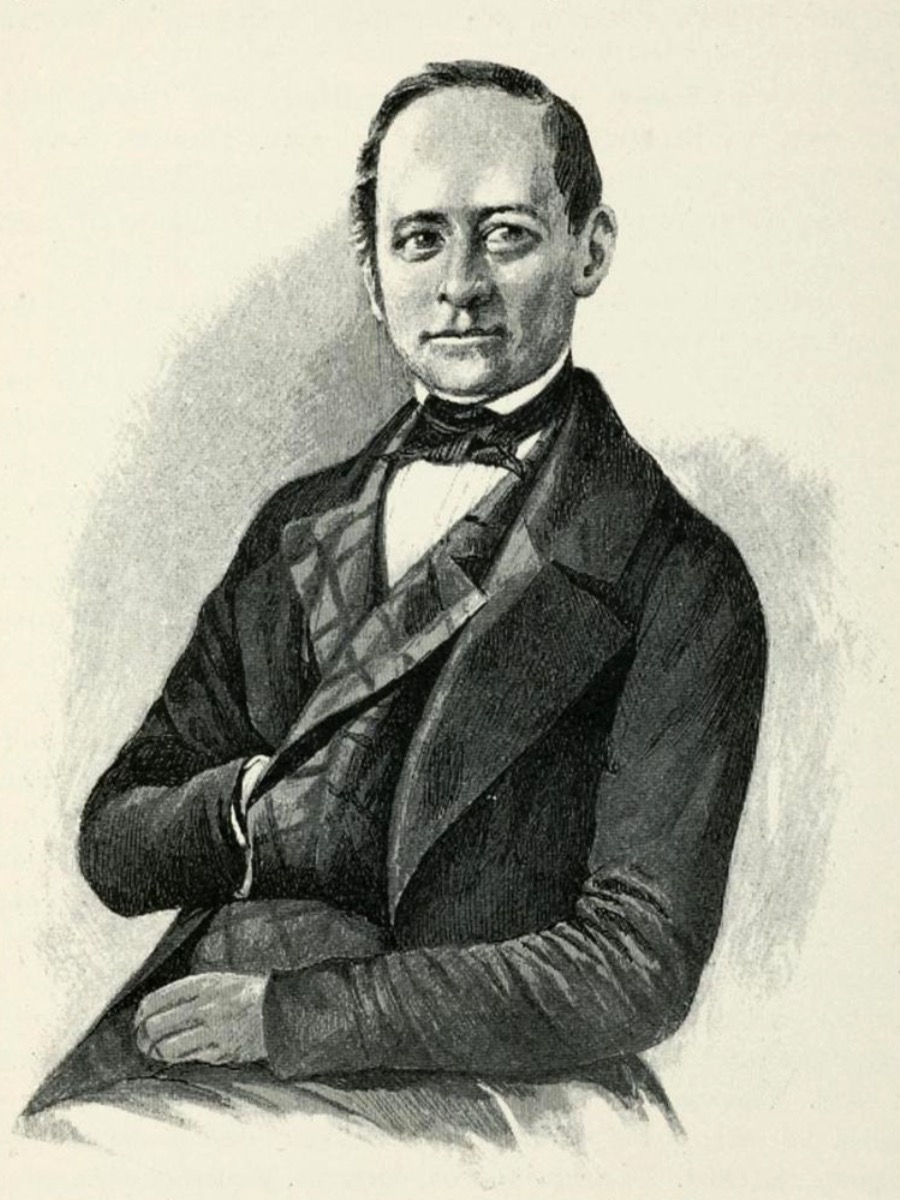
Леонтий Магницкий
Леонтий Филиппович Магницкий – Орус математиги, педагог. Москвадагы Математикалык жана навигациялык илимдер мектебинин математика мугалими, Орусиядагы биринчи математика боюнча окуу китебинин автору. Биринчи жолу орус тилине көбөйтүүчү, бөлүнүүчү, тамырдан көбөйтүүнү чыгаруу, миллион, биллион, триллио, квадриллион математикалык терминдерин киргизген.
Ондук бөлчөктөрдүн артыкчылыгы
Байыркы систематикалык бөлчөктөрдү Вавилондо биздин заманга чейин 4000 жыл мурда колдонушкан жана ал байыркы грек астрономдору аркылуу Батыш Европанын астрономдоруна келген, алар алтымыштык бөлчөктөр болгон. XVI кылымдын аягында, жашоонун баардык тармактарында бөлчөктөрдүн татаал эсептери кеңири колдонула баштаганда, башка систематикалык бөлчөктөр ондуктар пайда боло баштаган. Аларда бир он бөлүккө бөлүнгөн (ондуктар), а бир онунчу бөлүк кайра он бөлүккө (жүздүк) д.у.с. Ондук бөлчөктүн башка систематикалык бөлчөктөн өзгөчөлүгү , анын ошол эле системада негизделип, эсептин чыгарылышы жана бүтүн сандардын жазылышында. Ошонун негизинде жазуусу дагы, ондук бөлчөктүн амалдарынын эрежеси дагы бүтүн сандардыкы сыяктуу эле. Ондук бөлчөктөрдү жазууда бөлүктөрдүн аталыштарын (бөлүмдөрүн) белгилеп жазыштын кереги жок; бул белгилөө дал келген ээлеген сандын ордунда гана билинет. Биринчи бүтүн сан жазылат, ал сандын оң жагында үтүр коюлуп, үтүрдөн кийинки жазылган биринчи сан ондук сан болот.(бирдиктин онунчу бөлугү), экинчи сан-жүздүк, үчүнчү сан-миңдик д.у.с. үтүрдөн кийинки турган сандар ондук белгилер деп аталат.
Ондук бөлчөктөрдөгү арифметикалык амалдар
Арифметикада кандай аткарылаарын карап көрөлү:
Ондук бөлчөктөрдү кошууда жана алууда мындай кылышат:
1. эгер керек болсо үтүрдөн кийинки сандардын санын оң жагына нөл кошуу менен ондук бөлчөктүн негизги касиетине таяп бирдей кылынат, ал болсо бөлчөктүн көлөмүнө таасирин тийгизбейт.
2. Бөлчөктөрдү алардын үтүрлөрү биринин астына бири дал келгендей кылып жазышат (разряддын астына разряд болгондой кылып)
3. Бүтүн сан сыяктуу үтүргө карабай кошуп/алуу. Оң тараптагы эң акыркы сандан баштап улам кийинки санга сол тарапка жылып бирден кошобуз.
4. Үтүрдү суммага коюу/айырмада үтүрдүн астына, топтоштуруп эсептөөчү бөлчөктөр
Ондук бөлчөктөрдү көбөйтүү
Бир ондук санды экинчисине көбөйтүүдө, аларды бүтүн сан сыяктуу көбөйтүп алыш керек, андан кийин алынган санды оң жагынан ондук белгилерине карата бөлүп алабыз анда эки көбөйтүлгөндү тең алабыз.Сүрөттү карап көбөйтүүдө мамыча түрүндө кандай туура жазылаарына көңүл бөл.
Эскертме: үтүрдү койгонго чейин нөлдү алып таштоого болбойт!
Ондук бөлчөктөрдү бөлүү
Ондук бөлчөктү натуралдык сандарга бөлүү үчүн кийинки алгоритмдерди эске алуу керек: Ондук бөлчөктү натуралдык санга мамыча түрүнүн эрежеси боюнча үтүргө маани бербей туруп бөлүү. Алынган жекеге үтүрдү коёбуз, качан бөлүнүүчүнүн бүтүн бөлүгүн бүткөндөн кийин. Эгерде бөлүнүүчүнүн бүтүн бөлүгү бөлүнүүчүдөн кичине болсо анда жекеге 0 бүтүн беребиз. Сүрөттө “бурчтук” бөлүүнүн жазуусу көрсөтүлгөн.
Эскертүү: Бөлүү процессинин сүрөттөлүшү эч качан бүтпөчүдөй.
Анда ондук бөлчөктө жекени так айта албайбыз, бирок кээ бир сандарга токтолуп жакындашкан жыйынтыкты ала алабыз.
Ондук бөлчөктөрдүн негизги касиеттери
Жогорудагы айтылгандардан кийин биз ондук бөлчөктү- бул кадимки эле сандар деп айта алабыз. Биз аларды кошуп, биринен бирин алып, көбөйтүп жана бөлө алабыз. Алар менен математикалык амалдарды туура кылуу эң башкы нерсе, анткени кетирилген арифметикалык катадан силердин ийгилигинер көз каранды. Силер бул нерселерди кантип кылышты билээриңерге талаш жок, ошондой болсо дагы бөлчөктөр менен иштей турган амалдардын ылайыгы үчүн силерге ондук бөлчөктөрдүн негизги касиетин эстеп калууну сунуштайбыз. Алар абдан жөнөкөй, биз аларды бир кичинекей эскертмеге чогулттук. Жүктөгүлө, чыгарып алгыла жана пайдалангыла!
Мисалдар
Глоссарий
Бүтүн сандар - бул натуралдык сандар, ошондой эле аларга карама-каршы сандар жана нөл саны.
Пайдалуу шилтемелер
Ондук бөлчөктүн арасынан эң көп колдонулган бөлчөк бул- 0,01, ал процент (пайыз) деп аталат жана 1% деп белгиленет. Пайыздык эсепти түшүнүү жана чыгара билүү ар бирибиз үчүн эң керек. Пайыздар адамдын жашоосундагы баардык тарапта кездешет. Бул түшүнүксүз Бухгалтерияны, финансыны статистиканы карай албайбыз. Жумушчуга айлык эсептеп берүү үчүн налогго которулуучу пайыздарды билиш керек; сактык банкынан счет ачыш үчүн же кредит алуу үчүн биз биринчи суммага төлөнүүчү пайызын көлөмүнө кызыгабыз. Ал эми соодада “пайыз” деген түшүнүк абдан көп колдонулат. Биз ар дайым арзандатып сатуу, арзандатуу, пайда ж.б.- мунун баары пайыздар. Азыркы жашап жаткан адамга маалыматтын чоң агымында жакшы аралашып, жашоонун ар кандай абалдарында туура чечим кабыл ала билиши зарыл. Бул үчүн пайыздык эсепти жакшы чыгаруу керек. Мындай эсептерди, маселелерди кандай чыгарыш керектигин кененирээк билгиңер келсе бул жерден карагыла: Проценттерге маселе: [Электрондук ресурс] // «Сёзнайка.ру», 2015. URL: http://www.seznaika.ru/matematika/ege/114-2009-12-06-18-08-29 (кайрылуу датасы: 20. 11. 2017)
Комикс – бул күчтүү айтылган. Дүйнөгө белгилүү карикатурист Ларри Гониканын жаңы китеби, ал Гарвар Университетинде математиканы алгебранын мектеп программасынын негизги темаларын камтыган интенсивдик курсунда окуйт жана окутат. Автор тирүү юморду алгебранын тарыхына экскурсия кылган жана “илимдердин ханышасынын” азыркы турмушубуздагы колдонулушуна көптөгөн мисалдарды келтирген. Гониктин татаал материалды кызыктуу, тамашалуу, жана жеңил кабыл ала тургандай кылып тартуулоодогу уникалдуу шыгы, ошондой эле кемчиликсиз таза түзүлүшү бул китепти мектеп окуучулары үчүн баардык каалагандар үчүн, өзүнүн математикалык шыгын формада кармагысы келгендер үчүн дагы эң сонун окуу куралы болуп саналат.: Алгебра. Табигый илим комикстерде. Ларри Гоник.: [Электрондукресурс] //Братчикова Надежда Владимировна, 2016-2017. URL:http://mathlife.ru/algebra . (кайрылуу датасы: 20. 11. 2017)
Библиография
- М. Я. Выгодский. Справочник по элементарной математике. Москва 1986.
- Задачи на проценты. : [Электронный ресурс] // «Сёзнайка.ру», 2015. URL: http://www.seznaika.ru/matematika/ege/114-2009-12-06-18-08-29 (дата обращения: 20. 11. 2017)
- Дроби: история дробей. История возникновения обыкновенных дробей.: [Электронный ресурс] // «ФБ», 2017 URL: http://fb.ru/article/236507/drobi-istoriya-drobey-istoriya-vozniknoveniya-obyiknovennyih-drobey (дата обращения: 20. 11. 2017)
- Алгебра. Естественная наука в комиксах. Ларри Гоник.:[Электронный ресурс] //Братчикова Надежда Владимировна, 2016-2017. URL:http://mathlife.ru/algebra . (дата обращения: 20. 11. 2017)
Ондук бөлчөктөр биринчи жолу Кытайда пайда болгон. Көк асман астындагы империясында аларды биздин заманга чейинки III кылымда колдонуп башташкан. Ондук бөлчөктүн тарыхы кытайлык математик Лю Хуэядан башталган, ал аларды ал квадраттык тамырдан чыгарууда колдонууну сунуштаган.
Биздин эранын III кылымында ондук бөлчөктөр Кытайда салмак менен көлөмдү эсептөөдө колдонула баштады. Акырындап алар математикага тереңирээк сүңгүп кире баштаган. Ал эми Европада ондук бөлчөктөр алда канча кеч колдолуна баштаган.
Бирок кытайлыктардан көз карандысыз ондук бөлчөктөрдү байыркы Самарканд шаарынан астроном аль-Каши ачкан. Ал ХV кылымда жашап жана эмгектенген. Ал өзүнүн теориясын “арифметикага ачкыч” деген трактатында берген, ал 1427 жылы жарыкка чыккан. Аль-Каши бөлчөктөрдүн жаңы формада жазылышын колдонууну сунуштаган. Эми бүтүн дагы бөлчөктүү бөлүгү бир катарда жазылат. Аларды бөлүүдө самарканддык окумуштуу үтүрдү пайдаланган эмес. Ал бүтүн санды жана бөлчөктүү бөлүгүн кызыл жана кара сыяны колдонуу менен жазган. Кээде Аль-Каши аларды бөлүү үчүн вертикалдык сызыкты дагы пайдаланган.
Бөлчөктүн жаңы түрлөрү Европалык математиктердин эмгектеринде XIII кылымдан баштап пайда боло баштаган. Бирок алар аль-Кашинин эмгектерин жана кытайлыктардын тапкандарын билишкен эмес экендигин айтып коюшубуз керек. Ондук бөлчөктөр Иордан Неморариянын эмгектеринде дагы пайда болгон. Андан кийин XVI кылымда француз окумуштуусу “Математикалык канонду” жазган, анда тригонометриялык таблица камтылган. Алардан Виет ондук бөлчөктөрдү алган. Бүтүн жана бөлчөк жагын айырмалаш үчүн окумуштуу вертикалдык сызыкчаны жана ар кандай көлөмдөгү шрифтерди пайдаланган. Бирок булар илимдеги кээ бир гана жекече окуялар болгон.
Европада ондук бөлчөктөрдүн күнүмдүк маселелерин чечүү кичине кечирээк башталган. Бул болсо XVI кылымдын аягында голландиялык окумуштуу Симон Стевиндин эмгеги болгон. Ал 1585-жылы “Онунчу” деп аталган математикалык эмгегин чыгарган. Анда окумуштуу ондук бөлчөктөрдүн арифметикада, акча системасында жана көлөм менен ченди аныктоодо колдонуу теориясын айткан.
Стевин ошондой эле үтүрдү колдонгон эмес. Ал түшүнүктүү болуш үчүн ар бир сандын үстүнө ( же сандан кийин) ал сандын разрядынын номерин айланага койгон. Биринчи жолу үтүр ондук бөлчөктү 1592-жылы эки бөлүккө бөлгөн. Бирок Англияда үтүрдүн оордуна чекитти пайдаланышкан. Америка кошмо штаттарында азыркыга чейин ондук бөлчөктү ушундай чекит менен жазышат. Мындай бүтүн жана бөлчөктү бөлүп жазууда эки белгини тең пайдалана берүүнү алгачкылардын бири болуп шотландык математик Джон Непер сунуштаган. Ал өз оюн 1617-жылы айткан. Үтүрдү немец окумуштуусу Иоганн Кеплер дагы пайдаланган.
Бөлчөктөр жөнүндө толук теория азыркыдан аз гана айырмаланган, ал 1701-жылы жазылган арифметика бонча биринчи китепте Леонтий Филиппович Магницкий тарабынан берилген. “Арифметика” бир нече бөлүктөн турган. Бөлчөктөр туураалуу автор кененирээк “Сынык жана бөлүнгөн сандар жөнүндө” деген бөлүмүндө айтып берген. Магницкий сынган сандар менен амалдарды жүргүзүп, аларды ар кандай белгилеген.Кээде окуйсуң окуйсуң бирок эрежелерди такыр эстей албайсың. Силерге анча чоң эмес ырларды сунуштайбыз, алар силерге ондук бөлчөктөрдүн көбөйтүү жана бөлүүсүндө жардам берет.