Математика: Чыныгы сандар — различия между версиями
Azim (обсуждение | вклад) (→Сандар тарыхы) |
Admine2 (обсуждение | вклад) |
||
| (не показано 5 промежуточных версий 3 участников) | |||
| Строка 3: | Строка 3: | ||
==Сандар тарыхы== | ==Сандар тарыхы== | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Числа_вокруг_нас_кт.gif | + | <div class="show-for-large-up">{{center|[[Файл:Числа_вокруг_нас_кт.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Числа_вокруг_нас_кт.gif | + | <div class="hide-for-large-up">{{center|[[Файл:Числа_вокруг_нас_кт.gif]]}}</div> |
Азыркы жашообузду сандарсыз элестетүү кыйын. Алар бизди бардык тарабыбыздан курчап турат. Биз аларды күн сайын кездештиребиз жана ар кандай техникалык ыкмалардын жардамы менен аларга ондогон, жүздөгөн жана миңдеген амалдарды жасайбыз. Биз буга абдан көнгөндүктөн сандардын тарыхы бизди кызыктырбайт дагы, а көптөрү бул жөнүндө жөн гана ойлошпойт дагы. Бирок өткөндү билмейинче азыркыны түшүнүүгө болбойт, ошондуктан башатты түшүнүүгө аракет кылуу керек. Анда сандардын өнүгүү тарыхы кандай? Алар качан пайда болушкан, адамдар аларды түзүүгө кандайча жетишкен? Келгиле анда бул жөнүндө билели! | Азыркы жашообузду сандарсыз элестетүү кыйын. Алар бизди бардык тарабыбыздан курчап турат. Биз аларды күн сайын кездештиребиз жана ар кандай техникалык ыкмалардын жардамы менен аларга ондогон, жүздөгөн жана миңдеген амалдарды жасайбыз. Биз буга абдан көнгөндүктөн сандардын тарыхы бизди кызыктырбайт дагы, а көптөрү бул жөнүндө жөн гана ойлошпойт дагы. Бирок өткөндү билмейинче азыркыны түшүнүүгө болбойт, ошондуктан башатты түшүнүүгө аракет кылуу керек. Анда сандардын өнүгүү тарыхы кандай? Алар качан пайда болушкан, адамдар аларды түзүүгө кандайча жетишкен? Келгиле анда бул жөнүндө билели! | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Сандар тарыхы.jpg | + | <div class="show-for-large-up">{{center|[[Файл:Сандар тарыхы.jpg]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Сандар тарыхы.jpg | + | <div class="hide-for-large-up">{{center|[[Файл:Сандар тарыхы.jpg]]}}</div> |
| − | <div class="show-for-large-up">{{left|[[Файл: | + | <div class="show-for-large-up">{{left|[[Файл:5_books_Evklid.jpg|300px]]}}</div> |
| − | <div class="hide-for-large-up">{{left|[[Файл: | + | <div class="hide-for-large-up">{{left|[[Файл:5_books_Evklid.jpg|200px]]}}</div> |
Биринчи өнүккөн сандык система, Байыркы Грецияда курулган, өзүнө натуралдык гана сандарды жана алардын катышын камтыган (пропорция, азыркы түшүнүктө- рационалдык сандар). Бирок геометриянын жана астрономиянын максаттары үчүн бул жетишсиз экени бат эле белгилүү болгон, мисалы: квадраттын диагоналынын анын жактарынын узундугуна катышы натуралдык да рационалдык да боло албасы көрсөтүлгөн. Бул абалдан чыгуу үчүн Евдокс Книдский сандарга кошумча киргизүүнү киргизген, геометриялык чоңдук кеңири түшүнүгү, башкача айтканда кесиндинин узундугу, аянты жана көлөмү, Евдокстун теориясы- бул чыныгы сандардын геометриялык модели. | Биринчи өнүккөн сандык система, Байыркы Грецияда курулган, өзүнө натуралдык гана сандарды жана алардын катышын камтыган (пропорция, азыркы түшүнүктө- рационалдык сандар). Бирок геометриянын жана астрономиянын максаттары үчүн бул жетишсиз экени бат эле белгилүү болгон, мисалы: квадраттын диагоналынын анын жактарынын узундугуна катышы натуралдык да рационалдык да боло албасы көрсөтүлгөн. Бул абалдан чыгуу үчүн Евдокс Книдский сандарга кошумча киргизүүнү киргизген, геометриялык чоңдук кеңири түшүнүгү, башкача айтканда кесиндинин узундугу, аянты жана көлөмү, Евдокстун теориясы- бул чыныгы сандардын геометриялык модели. | ||
| Строка 20: | Строка 20: | ||
Сандардын өнүгүүсү жөнүндөгү түшүнүктүн тарыхын схема түрүндө көрсөтүүгө болот: | Сандардын өнүгүүсү жөнүндөгү түшүнүктүн тарыхын схема түрүндө көрсөтүүгө болот: | ||
| − | <div class="show-for-large-up">{{center|[[File: | + | <div class="show-for-large-up">{{center|[[File:San_pazl.png|500px]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[File: | + | <div class="hide-for-large-up">{{center|[[File:San_pazl.png|500px]]}}</div> |
<div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | ||
| Строка 31: | Строка 31: | ||
Сунушталган чыныгы сандарды сандык түз сызыктын жардамы менен көрүүгө болот. Эгерде түздүккө оң багытты көрсөтүп, баштапкы чекитти жана бир гана кесиндини тандаса, анда ар бир чыныгы санды ал түздүктөгү аныкталган чекитке дал келтирип коюуга болот жана кайрадан, ар бир чекит бир гана чыныгы санды көрсөтө алат. Ошондуктан «сандык түз сызык» термини дайыма көптөгөн чыныгы сандардын синоними катары пайдаланылат. Көптөгөн чыныгы сандар R латын тамгасы менен белгиленет. | Сунушталган чыныгы сандарды сандык түз сызыктын жардамы менен көрүүгө болот. Эгерде түздүккө оң багытты көрсөтүп, баштапкы чекитти жана бир гана кесиндини тандаса, анда ар бир чыныгы санды ал түздүктөгү аныкталган чекитке дал келтирип коюуга болот жана кайрадан, ар бир чекит бир гана чыныгы санды көрсөтө алат. Ошондуктан «сандык түз сызык» термини дайыма көптөгөн чыныгы сандардын синоними катары пайдаланылат. Көптөгөн чыныгы сандар R латын тамгасы менен белгиленет. | ||
| − | <div class="show-for-large-up">{{center|[[File: | + | <div class="show-for-large-up">{{center|[[File:Chislovaya_pryamaya.gif|500px]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[File: | + | <div class="hide-for-large-up">{{center|[[File:Chislovaya_pryamaya.gif|500px]]}}</div> |
Чыныгы сандар менен болгон арифметикалык амалдардын касиеттери. Алгебранын негизги закондору. | Чыныгы сандар менен болгон арифметикалык амалдардын касиеттери. Алгебранын негизги закондору. | ||
| Строка 46: | Строка 46: | ||
# a∙(b+c)=a∙b+a∙c. | # a∙(b+c)=a∙b+a∙c. | ||
# a∙1=a. | # a∙1=a. | ||
| − | # a∙[[File: | + | # a∙[[File:drob_1a.png|15px]]=1,a≠0. |
Бул касиеттер алгебранын негизги закондору деп аталат. | Бул касиеттер алгебранын негизги закондору деп аталат. | ||
| Строка 69: | Строка 69: | ||
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | <ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | ||
<li class="active"> | <li class="active"> | ||
| − | [[file:Пример_1_Вещественные_числа_кт_.gif | + | [[file:Пример_1_Вещественные_числа_кт_.gif]] |
</li> | </li> | ||
<li> | <li> | ||
| − | [[file:Пример_2_Вещественные_числа_кт.gif | + | [[file:Пример_2_Вещественные_числа_кт.gif]] |
</li> | </li> | ||
<li> | <li> | ||
| − | [[file:Пример_3_Вещественные_числа_кт.gif | + | [[file:Пример_3_Вещественные_числа_кт.gif]] |
</li> | </li> | ||
</ul> | </ul> | ||
| Строка 82: | Строка 82: | ||
==Глоссарий== | ==Глоссарий== | ||
| − | *'''Оң сандар'''- сан, | + | *'''Оң сандар'''- сан, нөлдөн чоң. |
*'''Терс сандар'''- минус (−) белгиси менен сандар, мисалы: −1, −2, −3 ж.б. минус бир, минус эки, минус үч ж.б. болуп окулат. | *'''Терс сандар'''- минус (−) белгиси менен сандар, мисалы: −1, −2, −3 ж.б. минус бир, минус эки, минус үч ж.б. болуп окулат. | ||
| − | *'''Бүтүн сандар''' – бул натуралдык сандар, | + | *'''Бүтүн сандар''' – бул натуралдык сандар, нөл саны, ошондой эле натуралдык сандарга карама-каршы сандар. |
*'''Натуралдык сандар''' - бул сандар, предметтерди саноо үчүн же бирдей предметтер арасындагы тигил же бул предметтин катар номерин көрсөтүү үчүн колдонулат. | *'''Натуралдык сандар''' - бул сандар, предметтерди саноо үчүн же бирдей предметтер арасындагы тигил же бул предметтин катар номерин көрсөтүү үчүн колдонулат. | ||
| − | *'''Рационалдык сандар''' - Бул сандарды кадимки бөлчөк, терс кадимки бөлчөк жана | + | *'''Рационалдык сандар''' - Бул сандарды кадимки бөлчөк, терс кадимки бөлчөк жана нөл саны түрүндө жазууга болот. |
*'''Иррационалдык сандар''' - санда, ондук жазууда чексиз, мезгилсиз ондук бөлчөктөрдү көрсөтөт. | *'''Иррационалдык сандар''' - санда, ондук жазууда чексиз, мезгилсиз ондук бөлчөктөрдү көрсөтөт. | ||
| Строка 131: | Строка 131: | ||
</div> | </div> | ||
| − | 1. Алгач араб сандары түз кесиндилерден гана турган, | + | 1. Алгач араб сандары түз кесиндилерден гана турган, нөлдөн бөлөгү, “сандардын мааниси алардын жазылышындагы бурчтарына дал келет” принциби боюнча түзүлгөн. Мисалы: нөл-бурчу жок, бир-бир бурч, эки-эки бурч ж.б |
| − | {{center|[[Файл:Арабские цифры в виде отрезков.jpg | + | {{center|[[Файл:Арабские цифры в виде отрезков.jpg]]}} |
2. Брахмагупта- индиялык математик, VII кылымда жашаган, биринчилерден болуп оң жана терс сандарды пайдаланган | 2. Брахмагупта- индиялык математик, VII кылымда жашаган, биринчилерден болуп оң жана терс сандарды пайдаланган | ||
| Строка 139: | Строка 139: | ||
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | <ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | ||
<li class="active"> | <li class="active"> | ||
| − | [[file:Брамагупта.png | + | [[file:Брамагупта.png]] |
</li> | </li> | ||
<li> | <li> | ||
| − | [[file:Леонардо_Фибоначчи.png | + | [[file:Леонардо_Фибоначчи.png]] |
</li> | </li> | ||
</ul> | </ul> | ||
| Строка 148: | Строка 148: | ||
3. Американын Индиана штатында: штаттын аймагында π санын '''4''' кө барабар деп эсептөө закону бар. | 3. Американын Индиана штатында: штаттын аймагында π санын '''4''' кө барабар деп эсептөө закону бар. | ||
| − | {{center|[[Файл:Америка_Кошмо_Штаттары.jpg | + | {{center|[[Файл:Америка_Кошмо_Штаттары.jpg]]}} |
4. Илимий коомдун көп өкүлдөрү π математикалык константа деп аташат, ал өзүнүн сырлары жана жашыруун маанилери бар сан. Эгерде бир нече изилдөөлөрдү карап көрсөк, бардык кылымдагы жана элдердеги окумуштуулар бул санга көп көңүл бөлүшкөн, ошондуктан биз оңой эле π жөнүндө эң кызыктуу фактыларды таба алдык. | 4. Илимий коомдун көп өкүлдөрү π математикалык константа деп аташат, ал өзүнүн сырлары жана жашыруун маанилери бар сан. Эгерде бир нече изилдөөлөрдү карап көрсөк, бардык кылымдагы жана элдердеги окумуштуулар бул санга көп көңүл бөлүшкөн, ошондуктан биз оңой эле π жөнүндө эң кызыктуу фактыларды таба алдык. | ||
| − | {{center|[[Файл: | + | {{center|[[Файл:7_faktov_pi_kyrg.mp4|400px|start=1]]}} |
</div> | </div> | ||
| Строка 164: | Строка 164: | ||
</div> | </div> | ||
| − | Дэвид Макдональд π санын үтүрдөн кийин даана 122 белгиге чейин нотага койгон. Механизми абдан жөнөкөй: гамманын ар бир музыкалык баскычына 0 | + | Дэвид Макдональд π санын үтүрдөн кийин даана 122 белгиге чейин нотага койгон. Механизми абдан жөнөкөй: гамманын ар бир музыкалык баскычына 0 дөн 9 га чейинки сан берилген. Негизи үчүн ля-минор тональносту алынган. Мында Пи саны бир башкача гармонияга жада калса “космостук” мелодияга айланган, анын аткарылышы π саны жөнүндөгү кызыктуу фактылар менен коштолот. |
| − | {{center|[[Файл:Музыка_числа_Пи.mp4 | + | {{center|[[Файл:Музыка_числа_Пи.mp4]]}} |
</div> | </div> | ||
| Строка 254: | Строка 254: | ||
</div> | </div> | ||
| − | + | <div class="sbstyle"> | |
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Тестти өтүңүз</div> | ||
| + | </div> | ||
| + | |||
| + | </div> | ||
</div> | </div> | ||
{{lang|Математика: Действительные числа (Вещественные числа)}} | {{lang|Математика: Действительные числа (Вещественные числа)}} | ||
Текущая версия на 08:54, 22 октября 2018
Содержание
Сандар тарыхы
Азыркы жашообузду сандарсыз элестетүү кыйын. Алар бизди бардык тарабыбыздан курчап турат. Биз аларды күн сайын кездештиребиз жана ар кандай техникалык ыкмалардын жардамы менен аларга ондогон, жүздөгөн жана миңдеген амалдарды жасайбыз. Биз буга абдан көнгөндүктөн сандардын тарыхы бизди кызыктырбайт дагы, а көптөрү бул жөнүндө жөн гана ойлошпойт дагы. Бирок өткөндү билмейинче азыркыны түшүнүүгө болбойт, ошондуктан башатты түшүнүүгө аракет кылуу керек. Анда сандардын өнүгүү тарыхы кандай? Алар качан пайда болушкан, адамдар аларды түзүүгө кандайча жетишкен? Келгиле анда бул жөнүндө билели!
Биринчи өнүккөн сандык система, Байыркы Грецияда курулган, өзүнө натуралдык гана сандарды жана алардын катышын камтыган (пропорция, азыркы түшүнүктө- рационалдык сандар). Бирок геометриянын жана астрономиянын максаттары үчүн бул жетишсиз экени бат эле белгилүү болгон, мисалы: квадраттын диагоналынын анын жактарынын узундугуна катышы натуралдык да рационалдык да боло албасы көрсөтүлгөн. Бул абалдан чыгуу үчүн Евдокс Книдский сандарга кошумча киргизүүнү киргизген, геометриялык чоңдук кеңири түшүнүгү, башкача айтканда кесиндинин узундугу, аянты жана көлөмү, Евдокстун теориясы- бул чыныгы сандардын геометриялык модели.
Абал биздин кылымга чейинки биринчи кылымдарда өзгөрө баштаган. Диофант Александрийский мурунку салттарга каршы бөлчөктөрдү дагы натуралдык сан катары караган, а өзүнүн “Арифметика” китебинин IV-сүндө бир жыйынтык жөнүндө жазган: “Сан рационалдык эмес экен”. Антикалык илимдин кыйрашынан кийин алдыңкы планга индиялык жана исламдык математика чыккан, алар үчүн ченөөнүн жана эсептөөнүн каалагандай жыйынтыгы сан болуп саналган. Бул көз караштар акырындап орто кылымдагы Европадан дагы өйдө болгон, ал жакта алгач рационалдык жана иррационалдык (акылсыз дегендей) сандар (аларды жалган, маанисиз, керең ж.б. дагы аташкан). Иррационалдык сандардын укугундагы толук теңдемелер Симон Стевиндин (XVI кылымдын аягы) эмгектери менен байланыштуу. Андан жүз жыл өткөндөн кийин Ньютон өзүнүн “Универсалдык арифметика” (1707) сында классикалык аныктаманы берген (чыныгы) сандар бирдик эталонун ченөөдө жыйынтыгынын катышы.
Сандардын өнүгүүсү жөнүндөгү түшүнүктүн тарыхын схема түрүндө көрсөтүүгө болот:
Чыныгы сандар түшүнүгү
Чыныгы, же болбосо анык сандар – математикалык абстракция, курчап турган дүйнөдөгү геометриялык жана физикалык ченөөлөрдүн зарылдыгынан келип чыккан, ошондой эле, тамырдан чыгаруу, логарифмаларды чыгаруу, алгебралык теңдемелерди эсептөө сыяктуу амалдарды аткаруу.
Сунушталган чыныгы сандарды сандык түз сызыктын жардамы менен көрүүгө болот. Эгерде түздүккө оң багытты көрсөтүп, баштапкы чекитти жана бир гана кесиндини тандаса, анда ар бир чыныгы санды ал түздүктөгү аныкталган чекитке дал келтирип коюуга болот жана кайрадан, ар бир чекит бир гана чыныгы санды көрсөтө алат. Ошондуктан «сандык түз сызык» термини дайыма көптөгөн чыныгы сандардын синоними катары пайдаланылат. Көптөгөн чыныгы сандар R латын тамгасы менен белгиленет.
Чыныгы сандар менен болгон арифметикалык амалдардын касиеттери. Алгебранын негизги закондору.
Анык сандар менен арифметикалык амалдарды аткарууга болот. Алар рационалдык сандар менен болгон амалдарын касиеттери сыяктуу канаттандырат.
- a+b=b+a.
- (a+b)+c=a+(b+c).
- a+0=a .
- a+(-a)=0.
- a∙b=b∙a.
- (a∙b)∙c=a∙(b∙c).
- a∙(b+c)=a∙b+a∙c.
- a∙1=a.
- a∙
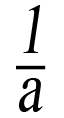=1,a≠0.
Бул касиеттер алгебранын негизги закондору деп аталат.
1 жана 5- касиеттер кошууга жана көбөйтүүгө дал келүүчү которуштуруу законун туюндурат;
2 жана 6- касиеттери айкалыштыруу законун туюндурат;
7-касиет көбөйтүүнүн кошууга салыштырмалуу бөлүштүрүү закону;
3 жана 8- касиеттери кошуу жана көбөйтүүгө дал келүү үчүн нейтралдык элементтин бар болушу;
4 жана 10-касиеттери нейтралдоочу элементтин дал келүүсүнүн бар болуусу.
Бул касиеттерден башка касиеттер бөлүнүп чыгат. Мисалы, a∙0=0. Чындыгында :
a∙0=a∙(b+(-b))= a∙b+a∙(-b)= a∙b+(-a∙b)=0
Мисалдар
Глоссарий
- Оң сандар- сан, нөлдөн чоң.
- Терс сандар- минус (−) белгиси менен сандар, мисалы: −1, −2, −3 ж.б. минус бир, минус эки, минус үч ж.б. болуп окулат.
- Бүтүн сандар – бул натуралдык сандар, нөл саны, ошондой эле натуралдык сандарга карама-каршы сандар.
- Натуралдык сандар - бул сандар, предметтерди саноо үчүн же бирдей предметтер арасындагы тигил же бул предметтин катар номерин көрсөтүү үчүн колдонулат.
- Рационалдык сандар - Бул сандарды кадимки бөлчөк, терс кадимки бөлчөк жана нөл саны түрүндө жазууга болот.
- Иррационалдык сандар - санда, ондук жазууда чексиз, мезгилсиз ондук бөлчөктөрдү көрсөтөт.
Пайдалуу шилтемелер
- “Чыныгы сандар” темасына видео сабак: [Электрондук ресурс] // Билим. Окутуу - Znaika TV. Знайка.ру YouTube, 2018 https://www.youtube.com/watch?v=WrIXyM_rv-Y (Катышуу датасы: 14.04.2018)
- “Анык сандардын модулу жана анын касиеттери” темасына видеосабак модулду түзүү түшүнүгүн жардам берет: [Электрондук ресурс] // Адамдар жана блогдор. YouTube, 2018 URL: https://www.youtube.com/watch?v=KbtNg7n9GpU (Катышуу датасы: 14.04.2018)
- Сергей Бобровдун “Сыйкырдуу эки мүйүздүү же Биздин кайраттуу досубуз Илья Алексеевич Камовдун белгисиз өлкөдөгү болуп көрбөгөндөй укмуштуу окуялары жөнүндөгү чыныгы окуялары” китебинде так илимди жана математиканы сүйүүчүлөр үчүн көптөгөн кызыктуу окуяларды кеңири айтып берет. Бул жерден силер математиканын өнүгүшү жөнүндө, анын техникадагы мааниси жөнүндө, айрыкча математиканын эң негизги бөлүгүнүн бири- математикалык анализ деп аталган бөлүгү жөнүндө биле аласыңар. Жеткиликтүү мисалдар менен дифференциалдык элементтер жана интегралдык эсептөөлөр менен таанышасыңар. Китепти мектептин жогорку класстарынын окуучулары жана кичинекей вундеркиндер үчүн өз алдынча окууга пайдаланууга болот: [Электрондук ресурс] // ЛитЛайф – адабият клубу URL: https://litlife.club/br/?b=282385 (Катышуу датасы: 14.04.2018)
Библиография
1. Гордый Рим трубил победу… Сергей Бобров.: [Электронный ресурс] // Antipodes Association Incorporated URL: http://www.antipodes.org.au/pr_pi_60.html (Дата посещения: 14.04.2018)
2. Совершенный Письмовник.: [Электронный ресурс] // Antipodes Association Incorporated URL: http://www.antipodes.org.au/pr_pi_all.html#Collection (Дата посещения: 14.04.2018)
3. Карл Эдуард Саган Контакт https: [Электронный ресурс] // ЛитЛайф - литературный клуб URL: https://litlife.club/br/?b=260441 (Дата посещения: 17.04.2018)
4. Сергей Бобров «Волшебный двурог, или Правдивая история небывалых приключений нашего отважного друга Ильи Алексеевича Камова в неведомой стране»: [Электронный ресурс] // ЛитЛайф - литературный клуб URL: https://litlife.club/br/?b=282385 (Дата посещения: 14.04.2018)
5. Факты о числе Пи.: [Электронный ресурс] // Удивительные факты для всех! 2013-2018 URL:http://amazing-facts.ru/science/fakty_o_chisle_pi.html (Дата посещения: 17.04.2018)
6. 10 удивительных визуализаций числа Пи: [Электронный ресурс] // DataReview.info URL: http://datareview.info/article/10-udivitelnyih-vizualizatsiy-chisla-pi/ (Дата посещения: 17.04.2018) 10 удивительных фактов о числе Пи: [Электронный ресурс] // 2013–2018 Пабли URL: http://www.publy.ru/post/25177 (Дата посещения: 17.04.2018)
7. Видеоурок на тему «Модуль действительного числа и его свойства»: [Электронный ресурс] // Люди и блоги YouTube, 2018 URL:https://www.youtube.com/watch?v=KbtNg7n9GpU (Дата посещения: 14.04.2018)
8. Видеоурок на тему «Вещественные числа» : [Электронный ресурс] //Образование. Обучение - Znaika TV. Знайка.ру YouTube, 2018 https://www.youtube.com/watch?v=WrIXyM_rv-Y (Дата посещения: 14.04.2018)
9. М. Я. Выгодский. Справочник по элементарной математике. Москва 1986.
1. Алгач араб сандары түз кесиндилерден гана турган, нөлдөн бөлөгү, “сандардын мааниси алардын жазылышындагы бурчтарына дал келет” принциби боюнча түзүлгөн. Мисалы: нөл-бурчу жок, бир-бир бурч, эки-эки бурч ж.б
2. Брахмагупта- индиялык математик, VII кылымда жашаган, биринчилерден болуп оң жана терс сандарды пайдаланган
3. Американын Индиана штатында: штаттын аймагында π санын 4 кө барабар деп эсептөө закону бар.
4. Илимий коомдун көп өкүлдөрү π математикалык константа деп аташат, ал өзүнүн сырлары жана жашыруун маанилери бар сан. Эгерде бир нече изилдөөлөрдү карап көрсөк, бардык кылымдагы жана элдердеги окумуштуулар бул санга көп көңүл бөлүшкөн, ошондуктан биз оңой эле π жөнүндө эң кызыктуу фактыларды таба алдык.
Дэвид Макдональд π санын үтүрдөн кийин даана 122 белгиге чейин нотага койгон. Механизми абдан жөнөкөй: гамманын ар бир музыкалык баскычына 0 дөн 9 га чейинки сан берилген. Негизи үчүн ля-минор тональносту алынган. Мында Пи саны бир башкача гармонияга жада калса “космостук” мелодияга айланган, анын аткарылышы π саны жөнүндөгү кызыктуу фактылар менен коштолот.
Америкалык астрофизик Карл Сагананын илимий-фантастикалык “Контакт” романында, окумуштуу Пи санынын экилик сиситемасын жазууга аракет кылган. Аны менен алар жерден сырткаркы акылдын бардыгы жөнүндө жыйынтыкка келишкен.
1998-жылы режиссеру Даррен Аронофски болгон “Пи: Баш аламандыкка ишенүү” көркөм фильми Санденс кинофестивалында драма фильминдеги эң жакшы режиссура сыйлыгын алган. Сюжети боюнча башкы каарман Пи санына байланыштуу аны акылынан адаштырган суроолорго жөнөкөй жоопторду издейт.
π санын кандайча көрсөтүү керектигин карап туруп, математика канчалык сулуу экендигин түшүнөсүң.
Бул суроо адамдарды жүздөгөн жылдар бою ойлонтуп келүүдө. Аны эстеп калуу үчүн эмнелерди кана ойлоп чыгышкан жок. π саны жөнүндөгү ыр бул нерсени батыраак кылууга жардам берет.
Кекеберлүү Рим жеңишти жайылткан
Сиракуз чебинде
Архимед эмгектеринде
Мен көп сыймыктанам
Бизге бүгүн окуш керек
Эскиликке ардак көрсөтүп
Биз жаңылбаш үчүн
Айланабыз туура санаса
Аракет кылуу гана керек
Жана да бардыгын кандай болгонундай эстеп калуу керек
Үч -14-15-92 жана алты!
Сергей Бобров
