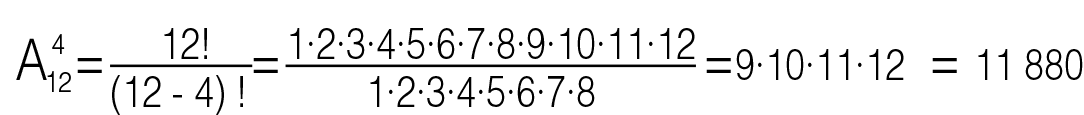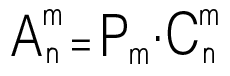Математика: Комбинаториканын негиздери — различия между версиями
Admine2 (обсуждение | вклад) |
Admine2 (обсуждение | вклад) |
||
| (не показано 8 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
<div class="row mat-bg"> | <div class="row mat-bg"> | ||
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> | <div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> | ||
| Строка 6: | Строка 5: | ||
==Комбинаториканын өнүгүү тарыхынан== | ==Комбинаториканын өнүгүү тарыхынан== | ||
| − | Адам баласы биздин заманга чейинки тарыхта эле тиги же бул предметти тандоо, аларды аныкталган тартипте жайгаштыруу, алардын арасынан ар кандай жайгашкандарынын эң ыңгайлуусун издеп табуу, | + | Адам баласы биздин заманга чейинки тарыхта эле тиги же бул предметти тандоо, аларды аныкталган тартипте жайгаштыруу, алардын арасынан ар кандай жайгашкандарынын эң ыңгайлуусун издеп табуу, мергенчилилер менчиликте жүрүшүп, жоокерлер – салгылаш учурунда, аспаптарды – жумуш учурунда эң мыкты абалдагысын тандоо сыяктуу маселелерди жолуктурушкан. Кийимдеги жасалгалоо, идиштеги сүрөттөр, жебенин учундагы канаттын сабынын жайгашышы дагы аныкталган ыкма менен кооздолгон. Өндүрүшүк жана коомдук мамилелердин мүмкүнчүлүккө жараша татаалданышы дагы барган сайын тартиби, иерархиясы, топтоштурулушу жөнүндөгү жалпы түшүнүктүн негизинде колдонулуп келген. Кол өнөрчүлүк жана соода-сатыктын өнүгүшү ошол багыт менен өнүгө баштаган. Комбинатордук көндүмдөр эс алуу учурунда да пайдалуу экендиги тастыкталган. Ал чуркоо жарышында, секирүүдө, дискти ыргытуу оюндары учурунда биринчи кезекте эсептөө билгичтигин, пладын ала план курууну жана каршылашынын кадамдарын алдын ала көрө билүү керек болгон. |
Мындан 35 кылым мурун египеттик фараон Тутанхамонду көмүү зыйнатында пирамидага кошо коюлган предметтердин арасынан байыркы “сенет” оюнунда колдонгон үч горизонт фигурасындагы досканын табылгандыгы. Кийинчерээк шахмат, шашки жана нардалар табылгандыгы. Булар табылган ар бир оюнолуучу фигуралар сунушталган оюнда фигуралардын ары бери жылдырылышы аныкталган айкалышты кармануу менен ким туура билген жана ойногон оюнчу гана натыйжада утушка ээ болоорун түшүнүшкөн. | Мындан 35 кылым мурун египеттик фараон Тутанхамонду көмүү зыйнатында пирамидага кошо коюлган предметтердин арасынан байыркы “сенет” оюнунда колдонгон үч горизонт фигурасындагы досканын табылгандыгы. Кийинчерээк шахмат, шашки жана нардалар табылгандыгы. Булар табылган ар бир оюнолуучу фигуралар сунушталган оюнда фигуралардын ары бери жылдырылышы аныкталган айкалышты кармануу менен ким туура билген жана ойногон оюнчу гана натыйжада утушка ээ болоорун түшүнүшкөн. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Комбинаториканын_өнүгүү_тарыхы.mp4 | + | <div class="show-for-large-up">{{center|[[Файл:Комбинаториканын_өнүгүү_тарыхы.mp4]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Комбинаториканын_өнүгүү_тарыхы.mp4 | + | <div class="hide-for-large-up">{{center|[[Файл:Комбинаториканын_өнүгүү_тарыхы.mp4]]}}</div> |
<div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | ||
| Строка 19: | Строка 18: | ||
Комбинато́рика — дисктреттик объектилерди, көптүктөр (айкалышы, ордун которуусу, жылдырылышы жана элементтерин саноодо) жана алар менен катыштар (айталы, жеке тартипте); латын сөзүнөн combinare которгондо – бириктирүү, айкалышы деп түшүндүрөт. Комбинаторика математиканын башка чөйрөлөрү менен да байланышкан – алгебра, геометрия, ыктымалдуулук теориясы жана билимдин ар түрдүү чөйрөлөрүндө да колдонулат. | Комбинато́рика — дисктреттик объектилерди, көптүктөр (айкалышы, ордун которуусу, жылдырылышы жана элементтерин саноодо) жана алар менен катыштар (айталы, жеке тартипте); латын сөзүнөн combinare которгондо – бириктирүү, айкалышы деп түшүндүрөт. Комбинаторика математиканын башка чөйрөлөрү менен да байланышкан – алгебра, геометрия, ыктымалдуулук теориясы жана билимдин ар түрдүү чөйрөлөрүндө да колдонулат. | ||
| − | Жөнөкөй бир мисал карап көрөлү. Мейли, краска куюлган 4 челек бар: кызыл (К), сары (С), жашыл (Ж) жана күрөң (Кң), жана биз аларды коробкаларга ар биринде ар башка эки челектен кылып | + | Жөнөкөй бир мисал карап көрөлү. Мейли, краска куюлган 4 челек бар: кызыл (К), сары (С), жашыл (Ж) жана күрөң (Кң), жана биз аларды коробкаларга ар биринде ар башка эки челектен кылып салышыбыз керек болот. Биз аны төмөндөгүчө аткарсак болот: |
| − | <div class="show-for-large-up">{{center|[[Файл:Простой_пример_—кт.gif | + | <div class="show-for-large-up">{{center|[[Файл:Простой_пример_—кт.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Простой_пример_—кт.gif | + | <div class="hide-for-large-up">{{center|[[Файл:Простой_пример_—кт.gif]]}}</div> |
Бизде алты ар түрдүү ыкма бар, эгерде бир коробкада сары жана кызыл болсо, анда ал кызыл жана сары челек краска менен бирдей болот. Бирок, эгерде бир түгөй түстөр менен белгилей турган болсок, анда он эки ыкма бар, анткени кызыл-сары түс менен сары-кызылдын айырмасы бар болот. | Бизде алты ар түрдүү ыкма бар, эгерде бир коробкада сары жана кызыл болсо, анда ал кызыл жана сары челек краска менен бирдей болот. Бирок, эгерде бир түгөй түстөр менен белгилей турган болсок, анда он эки ыкма бар, анткени кызыл-сары түс менен сары-кызылдын айырмасы бар болот. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Простой_пример_1.gif | + | <div class="show-for-large-up">{{center|[[Файл:Простой_пример_1.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Простой_пример_1.gif | + | <div class="hide-for-large-up">{{center|[[Файл:Простой_пример_1.gif]]}}</div> |
<div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | ||
| Строка 60: | Строка 59: | ||
Андан соң, ар бир санга 2ден кесинди туташтырабыз. Алардан ары улап ар бир кесиндинин учуна 1, 4, 7 сандарын жазабыз. Жыйынтыгы: 14, 17, 41 47, 71, 74 болот. Б. А. баары 6 сан болот. Бул схема даракка окшош болгондуктан “дарак” деп аталат. | Андан соң, ар бир санга 2ден кесинди туташтырабыз. Алардан ары улап ар бир кесиндинин учуна 1, 4, 7 сандарын жазабыз. Жыйынтыгы: 14, 17, 41 47, 71, 74 болот. Б. А. баары 6 сан болот. Бул схема даракка окшош болгондуктан “дарак” деп аталат. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Пример 2 2 способ.gif | + | <div class="show-for-large-up">{{center|[[Файл:Пример 2 2 способ.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Пример 2 2 способ.gif | + | <div class="hide-for-large-up">{{center|[[Файл:Пример 2 2 способ.gif]]}}</div> |
<div class="textblock">{{center|Көбөйтүүнүн эрежеси. Эгерде А объектини m ыкма менен жана эгерде ар бир жолкуда В объектини п ыкма менен тандалса, | <div class="textblock">{{center|Көбөйтүүнүн эрежеси. Эгерде А объектини m ыкма менен жана эгерде ар бир жолкуда В объектини п ыкма менен тандалса, | ||
| Строка 70: | Строка 69: | ||
'''Чыгарылышы''': | '''Чыгарылышы''': | ||
| − | Биринчи эки орунду санды үч ыкма менен тандоого болот. Биринчи санды | + | Биринчи эки орунду санды үч ыкма менен тандоого болот. Биринчи санды тандаган соң, экинчи санды калган сандардан эки ыкма менен тандаса болот. Андан соң, изделүүчү үч маанилүү сандын жалпы саны 3*2 санын көбөйтүндүсүнө, б.а. 6га барабар болот. |
'''Жообу''': 6 саны. | '''Жообу''': 6 саны. | ||
| Строка 102: | Строка 101: | ||
'''Комбинаториканын касиеттери:''' | '''Комбинаториканын касиеттери:''' | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Шахматная_доска_абстрация.jpg | + | <div class="show-for-large-up">{{center|[[Файл:Шахматная_доска_абстрация.jpg]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Шахматная_доска_абстрация.jpg | + | <div class="hide-for-large-up">{{center|[[Файл:Шахматная_доска_абстрация.jpg]]}}</div> |
Которулуштуруу деп, элементтери тартиби менен жайгашкан көптүк аталат. N элементтен турган мүмкүн болушунча которулуштуруу бул формула менен эсептелинет: Pn = n! | Которулуштуруу деп, элементтери тартиби менен жайгашкан көптүк аталат. N элементтен турган мүмкүн болушунча которулуштуруу бул формула менен эсептелинет: Pn = n! | ||
| Строка 122: | Строка 121: | ||
''Чыгарылышы''. | ''Чыгарылышы''. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Пример № 5.png | + | <div class="show-for-large-up">{{center|[[Файл:Пример № 5.png]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Пример № 5.png | + | <div class="hide-for-large-up">{{center|[[Файл:Пример № 5.png]]}}</div> |
n элементтен турган жана ар бир көптүктөгү k элементи бар көптүктөрдү n элементтен турган k элементтүү айкалышуу деп аталат. (Айкалышуу элементтеринен гана айырмаланат, тартиби маанилүү эмес: : ab жана ba –бул тиги да бул да айкалышуу) жана бул формула менен эсептелинет: | n элементтен турган жана ар бир көптүктөгү k элементи бар көптүктөрдү n элементтен турган k элементтүү айкалышуу деп аталат. (Айкалышуу элементтеринен гана айырмаланат, тартиби маанилүү эмес: : ab жана ba –бул тиги да бул да айкалышуу) жана бул формула менен эсептелинет: | ||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:formula_razme.png|100px]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:formula_razme.png|100px]]}}</div> |
Орун алмашуу, которулуу, айкаыштыруу бул барабарсыздык менен байланышат: | Орун алмашуу, которулуу, айкаыштыруу бул барабарсыздык менен байланышат: | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Число размещений, перестановок и сочетаний.png | + | <div class="show-for-large-up">{{center|[[Файл:Число размещений, перестановок и сочетаний.png]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Число размещений, перестановок и сочетаний.png | + | <div class="hide-for-large-up">{{center|[[Файл:Число размещений, перестановок и сочетаний.png]]}}</div> |
| − | |||
| Строка 142: | Строка 140: | ||
==Ыктымалдуулук. Негизги түшүнүктөр== | ==Ыктымалдуулук. Негизги түшүнүктөр== | ||
| − | Ыктымалдуулук теориясында бир нече жолу кубулуштарды, тажрыйбаларды, эксперименттерди байкоо текшрүү (сыноо) деп аталат. Текшерүү (сыноонун) жыйынтыгын окуя деп айтабыз. Мисалы, экзамен тапшыруу- бул сыноо; аныкталган баа алуу – бул окуя, оюн кубикти ыргытуу же өкчөө – бул сыноо; тиги же бул | + | Ыктымалдуулук теориясында бир нече жолу кубулуштарды, тажрыйбаларды, эксперименттерди байкоо текшрүү (сыноо) деп аталат. Текшерүү (сыноонун) жыйынтыгын окуя деп айтабыз. Мисалы, экзамен тапшыруу- бул сыноо; аныкталган баа алуу – бул окуя, оюн кубикти ыргытуу же өкчөө – бул сыноо; тиги же бул тарабы менен түшүү же упайдын саны – бул окуя. |
Ыктумалдуулук – бул окуянын пайда болуш мүмкүндүгүн мүнөздөөчү сан. Ар бир мүмкүн болгон сыноонун жыйынтыкгы элементардык жыйынтык деп аталат. | Ыктумалдуулук – бул окуянын пайда болуш мүмкүндүгүн мүнөздөөчү сан. Ар бир мүмкүн болгон сыноонун жыйынтыкгы элементардык жыйынтык деп аталат. | ||
| − | + | Р нын ыктымалдуулугу А окуясынын ошол окуяга карата боло (ишке аша) турган сандын, баардык мүмкүн болгон элементардык жыйынтыкка дал келбеген жалпы топту түзүүчү катышы болот. Р ыктымалдуулук А окуясын Р = m/n , мында m- элементардык жыйынтык; n – сыноодогу баардык мүмкүн болгон элементардык жыйынтыгы, Анын ылайыктуу элементардык жыйынтыгын аныктоочу формула. | |
Маселе | Маселе | ||
Алты бирдей жасалган корточкага К, Б, И, К, Е, Ш тамгалары жазылган. Карточкалар аралаштырылып кокустук боюнча бир катарга тизилет. Натыйжада БИШКЕК деп жазылып калгандай ыктымалдуулук эмнеге барабар болоорун тапкыла. | Алты бирдей жасалган корточкага К, Б, И, К, Е, Ш тамгалары жазылган. Карточкалар аралаштырылып кокустук боюнча бир катарга тизилет. Натыйжада БИШКЕК деп жазылып калгандай ыктымалдуулук эмнеге барабар болоорун тапкыла. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Задача_Бишкек.gif | + | <div class="show-for-large-up">{{center|[[Файл:Задача_Бишкек.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Задача_Бишкек.gif | + | <div class="hide-for-large-up">{{center|[[Файл:Задача_Бишкек.gif]]}}</div> |
'''Чыгарылышы'''. | '''Чыгарылышы'''. | ||
| Строка 169: | Строка 167: | ||
Маселени чыгаруу үчүн маселенин коюлуш шартына карата элементтерди өз ара жайгаштырууну колдонуу керек. Дыйкан бул жерде эчкини алып өтүү менен башташ керек болот. Андан соң жээке келип карышкырды тиги жээке алып келип кайра өзү менен кошо эчкини берки жээке ала кетиши керек болот. Ал жактан эчкини таштап капустаны тиги карышкыр турган жээкке алып келиш керек. Андан соң кайтып келип эчкини алып өтөт. | Маселени чыгаруу үчүн маселенин коюлуш шартына карата элементтерди өз ара жайгаштырууну колдонуу керек. Дыйкан бул жерде эчкини алып өтүү менен башташ керек болот. Андан соң жээке келип карышкырды тиги жээке алып келип кайра өзү менен кошо эчкини берки жээке ала кетиши керек болот. Ал жактан эчкини таштап капустаны тиги карышкыр турган жээкке алып келиш керек. Андан соң кайтып келип эчкини алып өтөт. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Задача_Волк_коза_капутса.gif | + | <div class="show-for-large-up">{{center|[[Файл:Задача_Волк_коза_капутса.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Задача_Волк_коза_капутса.gif | + | <div class="hide-for-large-up">{{center|[[Файл:Задача_Волк_коза_капутса.gif]]}}</div> |
<div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | ||
| Строка 181: | Строка 179: | ||
Пандигиталдык сандары бар маселелерди логикалык сыяктуу эле керек болсо андан да жөнөкөй чыгарылат, анткени комбинатордук объектилер өзүнө сандарды камтыйт. | Пандигиталдык сандары бар маселелерди логикалык сыяктуу эле керек болсо андан да жөнөкөй чыгарылат, анткени комбинатордук объектилер өзүнө сандарды камтыйт. | ||
| − | + | Ондук эсептөө системасындагы пандигиталдык эң кичине сан 123456789 саны эсептелинет. 987654321 ге 8ди көбөйткөндүн натыйжасында пайда болот. Бул 987654321 саны дагы пандигиталдык сан болуп саналат. Бул саны дагы көбөйтүүнүн натыйжасында өзүнүн пандигиталдуулугун сактайт: | |
- 2ге 123456789 ∙ 2 = 246913578, | - 2ге 123456789 ∙ 2 = 246913578, | ||
| Строка 193: | Строка 191: | ||
Мисал катары башка санды санга 2, 4, 5, жана 7 (коэффициентке) көбөйтүүдө пандигиталдуулугун сактаган сан катары 1098765432 келтирсек болот. Эгерде 123456789ны 8ге жана 9га көбөйтсөк бул сандын толук палиндрому келип чыгат. Эгерде көбөйүүчүнү жана кошулуучуларды 1ге чоңойтсок, жыйынтыгы ондо экиге чейинки разраддагы 1 1диктен турган сан пайда болот. | Мисал катары башка санды санга 2, 4, 5, жана 7 (коэффициентке) көбөйтүүдө пандигиталдуулугун сактаган сан катары 1098765432 келтирсек болот. Эгерде 123456789ны 8ге жана 9га көбөйтсөк бул сандын толук палиндрому келип чыгат. Эгерде көбөйүүчүнү жана кошулуучуларды 1ге чоңойтсок, жыйынтыгы ондо экиге чейинки разраддагы 1 1диктен турган сан пайда болот. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Пандигитальные_квадраты.gif | + | <div class="show-for-large-up">{{center|[[Файл:Пандигитальные_квадраты.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Пандигитальные_квадраты.gif | + | <div class="hide-for-large-up">{{center|[[Файл:Пандигитальные_квадраты.gif]]}}</div> |
<div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | ||
| Строка 320: | Строка 318: | ||
# Пифагор | # Пифагор | ||
# Комбинаторика | # Комбинаторика | ||
| + | </div> | ||
| + | <div class="sbstyle"> | ||
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Тестти өтүңүз</div> | ||
| + | </div> | ||
| + | |||
</div> | </div> | ||
{{lang|Математика: Основы комбинаторики}} | {{lang|Математика: Основы комбинаторики}} | ||
Текущая версия на 09:01, 22 октября 2018
Содержание
Комбинаториканын өнүгүү тарыхынан
Адам баласы биздин заманга чейинки тарыхта эле тиги же бул предметти тандоо, аларды аныкталган тартипте жайгаштыруу, алардын арасынан ар кандай жайгашкандарынын эң ыңгайлуусун издеп табуу, мергенчилилер менчиликте жүрүшүп, жоокерлер – салгылаш учурунда, аспаптарды – жумуш учурунда эң мыкты абалдагысын тандоо сыяктуу маселелерди жолуктурушкан. Кийимдеги жасалгалоо, идиштеги сүрөттөр, жебенин учундагы канаттын сабынын жайгашышы дагы аныкталган ыкма менен кооздолгон. Өндүрүшүк жана коомдук мамилелердин мүмкүнчүлүккө жараша татаалданышы дагы барган сайын тартиби, иерархиясы, топтоштурулушу жөнүндөгү жалпы түшүнүктүн негизинде колдонулуп келген. Кол өнөрчүлүк жана соода-сатыктын өнүгүшү ошол багыт менен өнүгө баштаган. Комбинатордук көндүмдөр эс алуу учурунда да пайдалуу экендиги тастыкталган. Ал чуркоо жарышында, секирүүдө, дискти ыргытуу оюндары учурунда биринчи кезекте эсептөө билгичтигин, пладын ала план курууну жана каршылашынын кадамдарын алдын ала көрө билүү керек болгон.
Мындан 35 кылым мурун египеттик фараон Тутанхамонду көмүү зыйнатында пирамидага кошо коюлган предметтердин арасынан байыркы “сенет” оюнунда колдонгон үч горизонт фигурасындагы досканын табылгандыгы. Кийинчерээк шахмат, шашки жана нардалар табылгандыгы. Булар табылган ар бир оюнолуучу фигуралар сунушталган оюнда фигуралардын ары бери жылдырылышы аныкталган айкалышты кармануу менен ким туура билген жана ойногон оюнчу гана натыйжада утушка ээ болоорун түшүнүшкөн.
Комбинаторика түшүнүгү
Комбинато́рика — дисктреттик объектилерди, көптүктөр (айкалышы, ордун которуусу, жылдырылышы жана элементтерин саноодо) жана алар менен катыштар (айталы, жеке тартипте); латын сөзүнөн combinare которгондо – бириктирүү, айкалышы деп түшүндүрөт. Комбинаторика математиканын башка чөйрөлөрү менен да байланышкан – алгебра, геометрия, ыктымалдуулук теориясы жана билимдин ар түрдүү чөйрөлөрүндө да колдонулат.
Жөнөкөй бир мисал карап көрөлү. Мейли, краска куюлган 4 челек бар: кызыл (К), сары (С), жашыл (Ж) жана күрөң (Кң), жана биз аларды коробкаларга ар биринде ар башка эки челектен кылып салышыбыз керек болот. Биз аны төмөндөгүчө аткарсак болот:
Бизде алты ар түрдүү ыкма бар, эгерде бир коробкада сары жана кызыл болсо, анда ал кызыл жана сары челек краска менен бирдей болот. Бирок, эгерде бир түгөй түстөр менен белгилей турган болсок, анда он эки ыкма бар, анткени кызыл-сары түс менен сары-кызылдын айырмасы бар болот.
Комбинаториканын негизги формулалары
1-миcал. Тарелкада 5 алма жана 4 апельсин салынган. Канча ыкма менен бир жемишти тандоого болот.
Чыгарылышы: Тапшырманын шарты боюнча алманы 5 ыкма, ал эми апельсинди 4 ыкма менен тандоого болот. Тапшырманын шарты болсо “же алма же пельсин” экендигин эске алуу менен 5+4=9 экенин табууга болот.
Жообу: 9 ыкма.
2-мисал. 1,4,7 сандарынан ар бири бир жолудан көп эмес колдонуп, канча эки маанилүү сан куроого болот?
Чыгарылышы: 1-ыкма: Варианттарды тандоо. Өткөрүп жибербес жана кайталабас үчүн бул сандарды өсүү тартибинде жазабыз. Алгач, 1 санына башталгандарды, андан сөн 4 жана 7 санына башталган сандарды жазабыз: 14, 17, 41, 47, 71, 74.
Жообу: 6 сан.
3-ыкма: Мүмкүн болгон вариантту дарак. Бул тапшырманы чыгаруу үчүн атайын схема курулган.
Жылдызча коёбуз. Андан ары ал жылдызчадан 3 кесинди чыгарабыз. Тапшырманын шарты боюнча 3 сан берилген – 1,4,7, кесиндинин учтарына бул сандарды жазабыз.
Андан соң, ар бир санга 2ден кесинди туташтырабыз. Алардан ары улап ар бир кесиндинин учуна 1, 4, 7 сандарын жазабыз. Жыйынтыгы: 14, 17, 41 47, 71, 74 болот. Б. А. баары 6 сан болот. Бул схема даракка окшош болгондуктан “дарак” деп аталат.
3-мисал. 1,4,7 сандарынан ар бири бир жолудан көп эмес колдонуп, канча эки маанилүү сан куроого болот?
Чыгарылышы: Биринчи эки орунду санды үч ыкма менен тандоого болот. Биринчи санды тандаган соң, экинчи санды калган сандардан эки ыкма менен тандаса болот. Андан соң, изделүүчү үч маанилүү сандын жалпы саны 3*2 санын көбөйтүндүсүнө, б.а. 6га барабар болот.
Жообу: 6 саны.
Факториал.
0! = 1
1!=1
2! = 1∙ 2 = 2
3! = 1∙ 2 ∙ 3 = 6
4! = 1∙ 2 ∙ 3 ∙ 4 =24
5! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120
6! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720
7! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 = 5 040
8! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 = 40 320
9! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 ∙ 9 = 362 880
10! = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 ∙ 9 ∙ 10 = 3 628 880
Комбинаториканын касиеттери:
Которулуштуруу деп, элементтери тартиби менен жайгашкан көптүк аталат. N элементтен турган мүмкүн болушунча которулуштуруу бул формула менен эсептелинет: Pn = n!
4-мисал. Финалдык чуркоодогу 8 катышуучу 8 чуркоочу тилкеге канча ыкма менен которулууга болот?
Чыгарылышы. P8 = 8! = 40 320
Акыркы көптүгү k (мында) боюнча n элементтен турган Аkn которулуусу ирээтелген көптүк деп аталып, k элементтен турган бул көптүк төмөнкү формула менен эсептелинет:5-Мисал.
12 окуучунун ичинен математика, физика, тарых жана география предметтери боюнча шаардык олимпадага катышууга бирден окуучуну тандоо керек. Ар бир катышуучу бирден гана предметке катышат. Канча ыкма менен аткарууга болот?
Чыгарылышы.
n элементтен турган жана ар бир көптүктөгү k элементи бар көптүктөрдү n элементтен турган k элементтүү айкалышуу деп аталат. (Айкалышуу элементтеринен гана айырмаланат, тартиби маанилүү эмес: : ab жана ba –бул тиги да бул да айкалышуу) жана бул формула менен эсептелинет:
Орун алмашуу, которулуу, айкаыштыруу бул барабарсыздык менен байланышат:
Ыктымалдуулук. Негизги түшүнүктөр
Ыктымалдуулук теориясында бир нече жолу кубулуштарды, тажрыйбаларды, эксперименттерди байкоо текшрүү (сыноо) деп аталат. Текшерүү (сыноонун) жыйынтыгын окуя деп айтабыз. Мисалы, экзамен тапшыруу- бул сыноо; аныкталган баа алуу – бул окуя, оюн кубикти ыргытуу же өкчөө – бул сыноо; тиги же бул тарабы менен түшүү же упайдын саны – бул окуя.
Ыктумалдуулук – бул окуянын пайда болуш мүмкүндүгүн мүнөздөөчү сан. Ар бир мүмкүн болгон сыноонун жыйынтыкгы элементардык жыйынтык деп аталат.
Р нын ыктымалдуулугу А окуясынын ошол окуяга карата боло (ишке аша) турган сандын, баардык мүмкүн болгон элементардык жыйынтыкка дал келбеген жалпы топту түзүүчү катышы болот. Р ыктымалдуулук А окуясын Р = m/n , мында m- элементардык жыйынтык; n – сыноодогу баардык мүмкүн болгон элементардык жыйынтыгы, Анын ылайыктуу элементардык жыйынтыгын аныктоочу формула.
Маселе Алты бирдей жасалган корточкага К, Б, И, К, Е, Ш тамгалары жазылган. Карточкалар аралаштырылып кокустук боюнча бир катарга тизилет. Натыйжада БИШКЕК деп жазылып калгандай ыктымалдуулук эмнеге барабар болоорун тапкыла.
Чыгарылышы. Изделүүчү ыктымалдуулук Р = m/n , мында m- элементардык жыйынтык; n – сыноодогу баардык мүмкүн болгон элементардык жыйынтыгы формуласы менен эсептелинет.
Биздин учурда n = 6! = 720 (6 карточканын жайгаштырылыш саны);
m = 2 (бул сөздөгү “К” тамгасынын эки жолу кайталанышы, калгандары бирден эле жолу).
Тыянак, Р=2/720=1/360.
Тапшырма: «Карышкыр, эчки жана капуста»
Дыйкан дарыянын аркы өйүзүнө карышкырды, эчкини жана капустаны алып өтүшү керек. Кайыкта орундук аз болгондуктан өзү менен кошо бирөөнү: карышкырды, эчкини же капустаны гана алып өтө алат. Бирок, карышкырды эчки менен калтырса карышкыр эчкини жеп салат, ал эми эчкини капуста менен калтырса капустаны эчки да жеп салат. Дыйкан эмне кылуу керек?
Маселени чыгаруу үчүн маселенин коюлуш шартына карата элементтерди өз ара жайгаштырууну колдонуу керек. Дыйкан бул жерде эчкини алып өтүү менен башташ керек болот. Андан соң жээке келип карышкырды тиги жээке алып келип кайра өзү менен кошо эчкини берки жээке ала кетиши керек болот. Ал жактан эчкини таштап капустаны тиги карышкыр турган жээкке алып келиш керек. Андан соң кайтып келип эчкини алып өтөт.
Комбинаторика программалоодо
Комбинаторика – бул ар кандай алгоритмдерди талдоодо, оптималдуу стратегияларды тандоодо керек болгон программисттердин чыныгы кенчи. Комбинатордук формулалар ыктымалдуулукту эсептөө үчүн, өзүнүн учурунда статистикалык гипотезаларды текшерүү үчүн керек болот. Программисттер комбинатордук маселелерди чыгарууда генерациялоо үчүн өзгөчө көңүлдү Generics Combinatorics программасы колдонгон пандигиталдык сандарга бурат.
Пандигиталдык сан деп, нөлдөн башталбаган жана бир сан кайра кайталанбаган сандарды айтабыз. Мисала 123456789.
Пандигиталдык сандары бар маселелерди логикалык сыяктуу эле керек болсо андан да жөнөкөй чыгарылат, анткени комбинатордук объектилер өзүнө сандарды камтыйт.
Ондук эсептөө системасындагы пандигиталдык эң кичине сан 123456789 саны эсептелинет. 987654321 ге 8ди көбөйткөндүн натыйжасында пайда болот. Бул 987654321 саны дагы пандигиталдык сан болуп саналат. Бул саны дагы көбөйтүүнүн натыйжасында өзүнүн пандигиталдуулугун сактайт:
- 2ге 123456789 ∙ 2 = 246913578,
- 4кө 123456789 ∙ 4 = 493827156,
- 5ке 123456789 ∙ 5 = 617283945,
- 7ге 123456789 ∙ 7 = 864197523.
Мисал катары башка санды санга 2, 4, 5, жана 7 (коэффициентке) көбөйтүүдө пандигиталдуулугун сактаган сан катары 1098765432 келтирсек болот. Эгерде 123456789ны 8ге жана 9га көбөйтсөк бул сандын толук палиндрому келип чыгат. Эгерде көбөйүүчүнү жана кошулуучуларды 1ге чоңойтсок, жыйынтыгы ондо экиге чейинки разраддагы 1 1диктен турган сан пайда болот.
Пайдалуу шилтемелер
Биздин жашообуз ар түрдүү программалардын көптүгүнөн турат. Тиги же бу тиешелүү программаны иштетиш үчүн туура келген сырсөздү киргизүү керек. Сырсөз катары программанын түрүнө карата сандар, сөздөр же сөздөрдүн айкалышын киргизүүгө туура келет. Комбинаторика музыкада, эмеректик ишмердүүлүктө, ар түрдүү оюндарда колдонулат (нарда, шахмат, шашка) ж.б. Кененирээк окугула: [Электрондык ресурс] // 2011-2017 Сила знаний URL: http://ya-znau.ru/znaniya/zn/80 (Катышуу датасы: 19.04.2018)
Толук чыгарылыштуу комбинатордук маселелерди төмөндө караса болот: [Электрондык ресурс] //mathprofi.ru, Александр Емелин, 2010-2018 URL: http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html (Катышуу датасы: 19.04.2018)
Оюн-тапшырмалар: «Ним». Мейли бир же бир нече топтогу предеттер болсун. Оюнчулар топтордон төмөнкү эрежеге ылайык кезеги менен предметтерди алышат: канча сандагы предметти бир нече топтордон бир гана жолу алууга уруксаат берилет. Көпчүлүккө белгилүү болгон жана жеңишке алып барган оюндун бир нече варианты бар. [Электрондык ресурс] //ЮЦ «Восстание-6» URL: https://logic-games.spb.ru/nim/ (Катышуу датасы: 22.04.2018)
Глоссарий
Дискре́ттүүлү (лат. discretus — бөлүнгөн, үзгүлтүктүү) – үзгүлтүксүзгө карама-каршы коюлган, үзгүлтүктүү касиет. Дискреттүүлүк түшүнүгү: бин нече туруктуу абалдардын ортосундагы өзгөрүүчү бин нерсе, мисалы мүнөттүк жебечеси дискреттүү кыймылдаган механикалык сааты, 1/60га айлананын бөлүгү; өзүнчө бөлүктөрдү түзгөн, үзгүлтүктүү, бөлчөктүк бир нерсе.
Палиндро́м (грек. πάλιν — «артка, кайра» жана башка.-грек. δρóμος — «чуркоо, кыймыл»)— эки тарабынан бирдей окула турган сан, тамгалар айкалышы, сөз же текст.
Пандигиталдык сандар – бул нолдөн баштабаган жана бир сан кайра кайталанбаган сан.
Су́тра (санскр. सूत्र sūtra IAST, «жип», пали: sutta) — байыркы абадияттардагы лаконикалык жана үзгүлтүктүү айтылыш, афоризмдер, кийинчерээк – ушундай айтылыштардын. Сутраларда ар түрдүү билимдери, дээрлик Байыркы Индиянын диний-философиялык окуучлары жазылган.
Библиография
- Комбинаторика: основные правила и формулы. : [Электронный ресурс] // 2011-2017 Сила знаний URL: http://ya-znau.ru/znaniya/zn/80 (Дата посещения: 19.04.2018)
- Задачи по комбинаторике. Примеры решений.: [Электронный ресурс] //mathprofi.ru, Александр Емелин, 2010-2018 URL: *http://www.mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html (Дата посещения: 19.04.2018)
- Сканворды, кроссворды и головоломки: [Электронный ресурс] // Пискунов Алексей © 2009-2018 http://www.graycell.ru/index.html (Дата посещения: 19.04.2018)
- Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика: М.: ФИМА, МЦНМО, 2006. — 400 с.
- Мир математики: в 40 т. Т.21: Ламберто Гарсия дель Сид. Замечательные числа. Ноль, 666, и другие бестии./Пер. с исп. –М.: Де Агостини, 2014. – 160 с.
Математика – жөнөкөй эрежелерге ылайык жана мааниге анча деле ээ эмес белгилөөлөрду колдонуу менен ойнолуучу жөн гана оюн.
Давид Гильберт
Оюн ырахат жана кубаныч эле тартуулабастан, толук кандуу эс алуу менен кошо интеллектти машыктырууга үйрөтөт. Математиканын жетишкендиктерин колдонуу жаңы оюндардын теориясын андан ары өнүктүрүү үчүн жана жаңы машыктырууча маселелерди түзүүдө кзмат кылаарын ырахат менен ырастоого болот.
Рубик кубиги – бул 27 бирдей кубка бөлүнгөн куб. Алгачкы абалында кубдун ар бир кырлары 6 түстүн бири менен боёлгон. Курч акылдуу механизм анын борбору менен кесилишкен каалагандай 9 кубиктин катмарын которууга мүмкүндүк берет. Мында чектеринин түстөрү аралашат. Маселе түрдүү түстөгү кубиктин кырларын алгачкы абалга алып келүүдө жатат. Теориялык жактан кубиктин каалагандай абалынан алгачкы абалына 23 жүрүштөн ашык эмес жүрүш менен келүүгө болот.
Мурун 1982-жылы дүйнөлүк чемпионатта Рубик кубигин чогултуунун ылдамдыгын 22,95 секунд деп көрсөткөн. А биздин учурда болсо балдарыбыз аз эле секунддада чогултат. Келгиле ынанып көрөлү
Жебечелер
Ар бир клеткадагы сандардан алардын саны алгачкы санга тең болуп, мында торчодогу сан эсепке алынбагандай кылып жебечелерди жүргүзүү керек. Жебечелер тигинен жана туурасынан жүргүзүлүшү керек. Жебечелер баардык бош клеткаларда болушу керек.
Судоку
1ден 9га чейинки сандардын бош торчосунда ар бир сапчадагы, ар бир мамычадагы жана ар бир квадраттагы сандар бирден гана жолу кездешкендей жайгаштыруу керек.
Лесенка
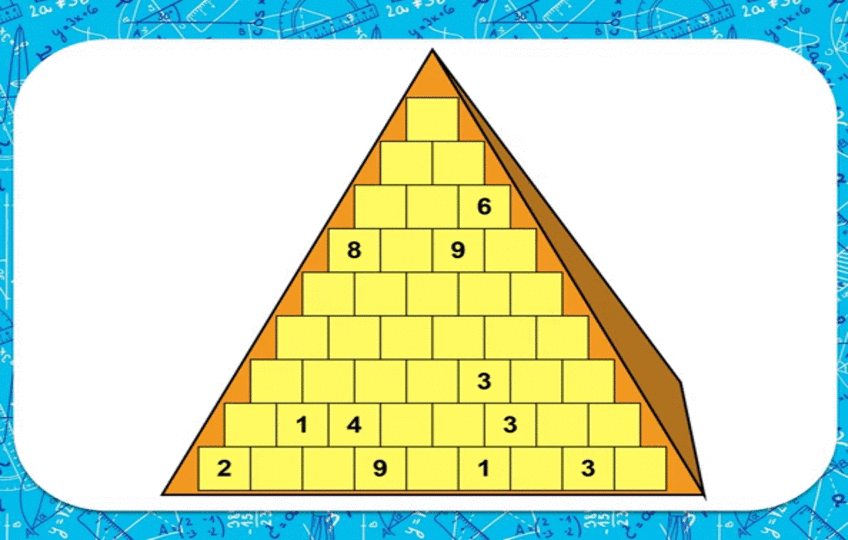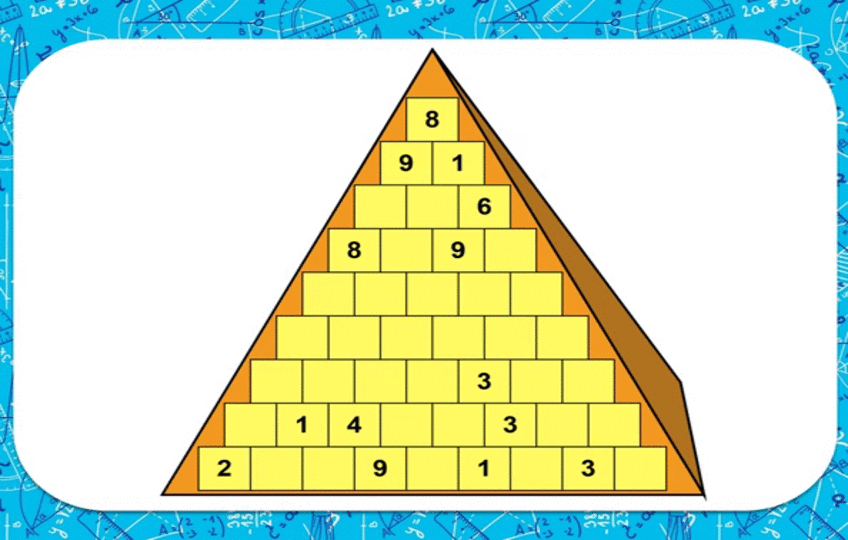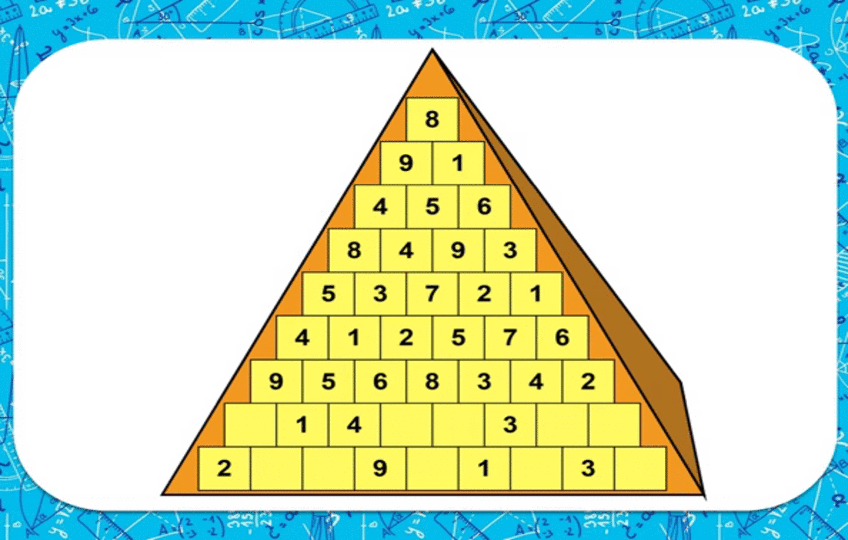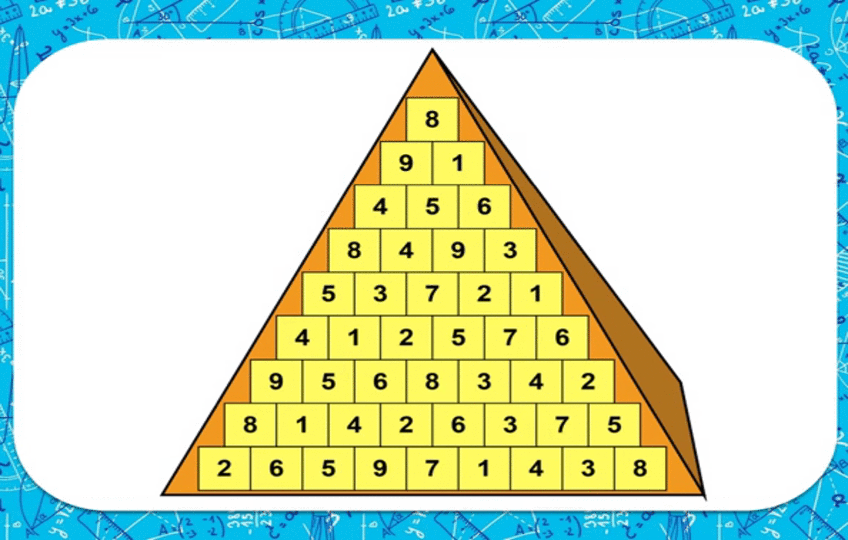
Пирамиданын чокусунан негизине чейинки сандары ар башка болгондой жолду табуу керек.
Пирамида
Уячалардын 1ден 9га чейин төмөнкү эрежеге ылайык толтуруу керек: уячадагы сан төмөнкү эки уячадагы сандардын суммасы же айырмасы катары болуп, пиармиданын ар бир сабындагы сандар кайталнбашы керек.
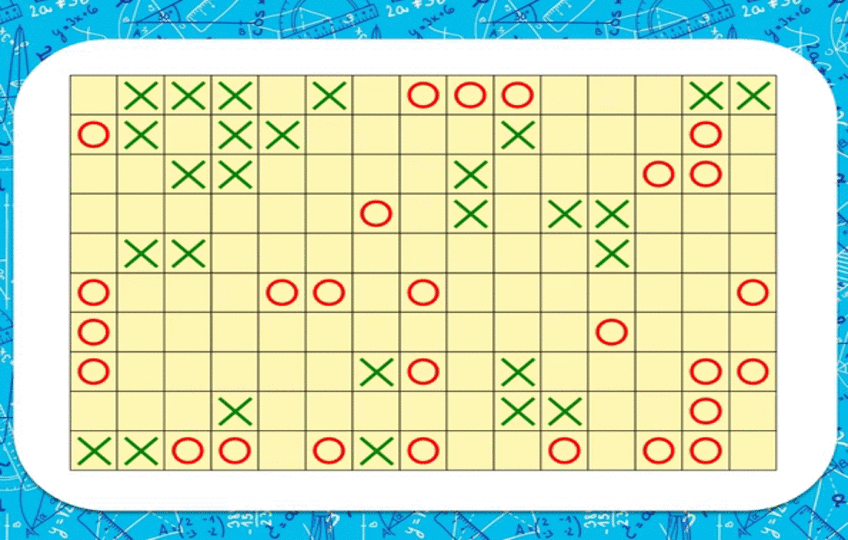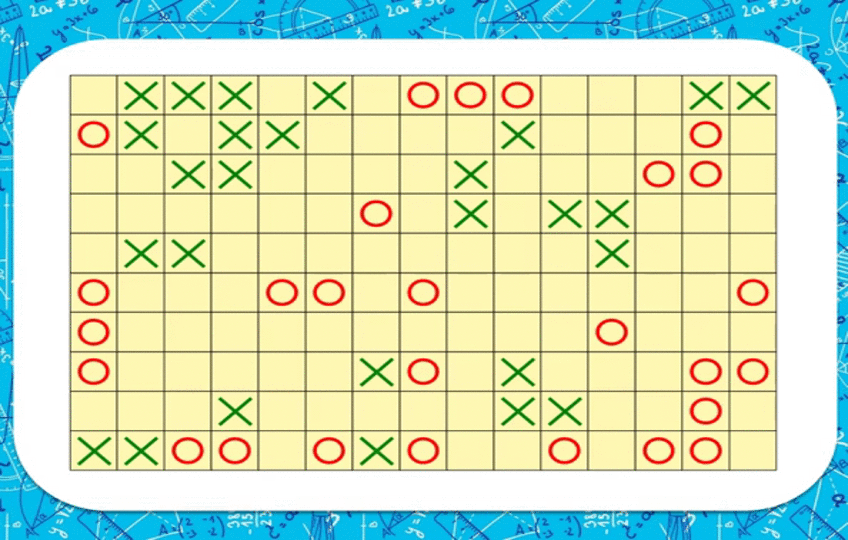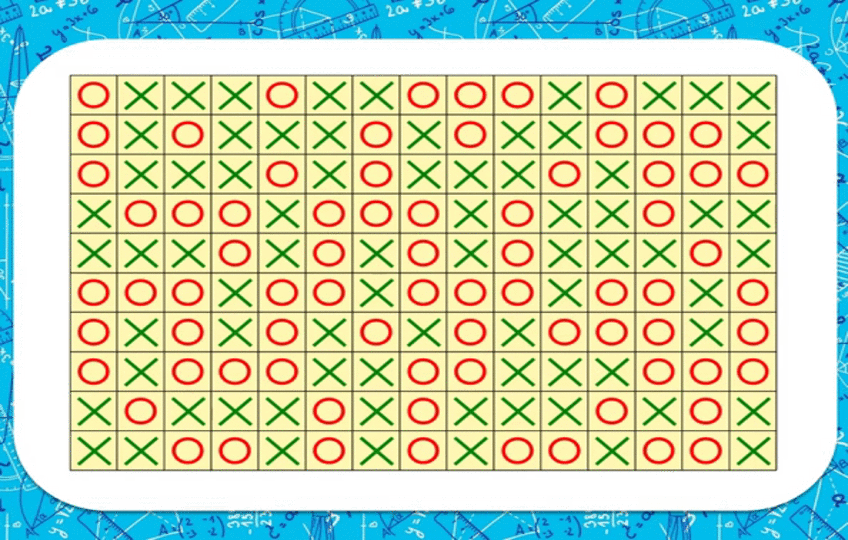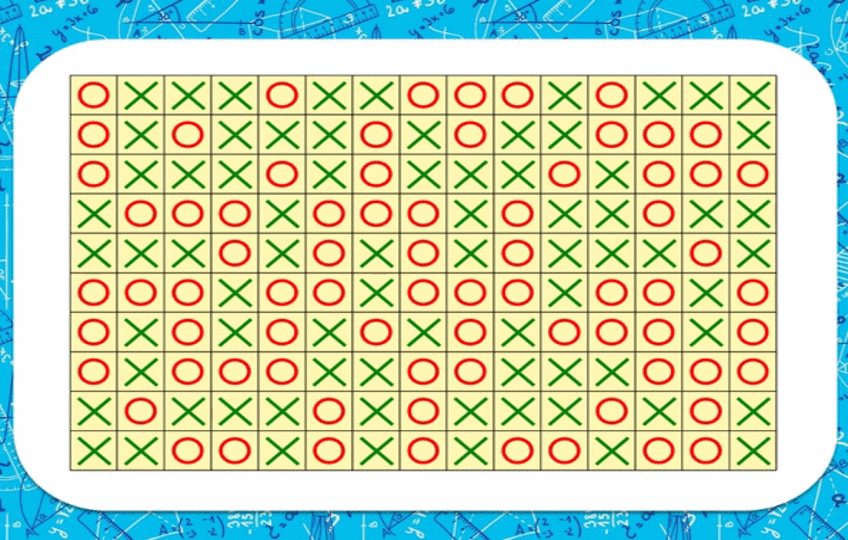
«Крестиктер-нөлдөр» Эң белгилүү байыркы оюн. Квадратта 9 клеткага чийилген, оюнчулар кезеги менен бош клеткаларга крестик жана нөлдөрдү бир ктарга 3өө болгондой кылышып чийишет, толтурушат. Муну биринчи жасаган жеңишке ээ болот.
Эгерде катасы жок толтурушса анда оюн тең-тең эсеби мене аяктайт. Каршылашың ката толтурган гана убакта утушка ээ болосуң. Эң туура жүрүш – бурчтагы клеткаларды ээлөө. Эгерде каршылашың сага жооп кылып ортоңку келтканы толтурса, анда анын утулганы.
Комбинатордук маселелерди чыгаруу бирге дайыма керек болот. Мисалы, филологго канча тамгалардын айкалышын эске алуу керек болот? Үч ар түрдүү кездемеден модельер канча ар түрдүү кийимди ойлоп табууга болот? Сатып алуучу буюмдардын тизмесин, сабактардын жүргүртмөсүн, футболдук команданын, Рубик кубигин, тамакты даярдоодо, класста окуучуларды отургузуу, текчелерге китептерди жайгаштыруу, столду жасалгоолоодо кантип түзүү керек? Көпчүлүк балдар оюндары чучу кулак кармоо менен башталат. Карта менен, ширенке менен же ромашка менен төлгө ачуу дагы комбинаторикага негизделген. Крек болсо поэзия дагы комбинаториканы унутта калтырбайт! Ыр жана музыка, графика – живопись искусствосу – мунун баары комбинаторжук процесстер. Бекеринен бул чөйрөдөгү “компьютерлер” таң калаардыктай ийгиликтерге жетишпесе керек. Аягында, баардык адамдар – ДНК молекуларларындагы гендердин комбинациялары экенин айтса болот.
Жооптору:
- Факториал
- Математика
- Пифагор
- Комбинаторика