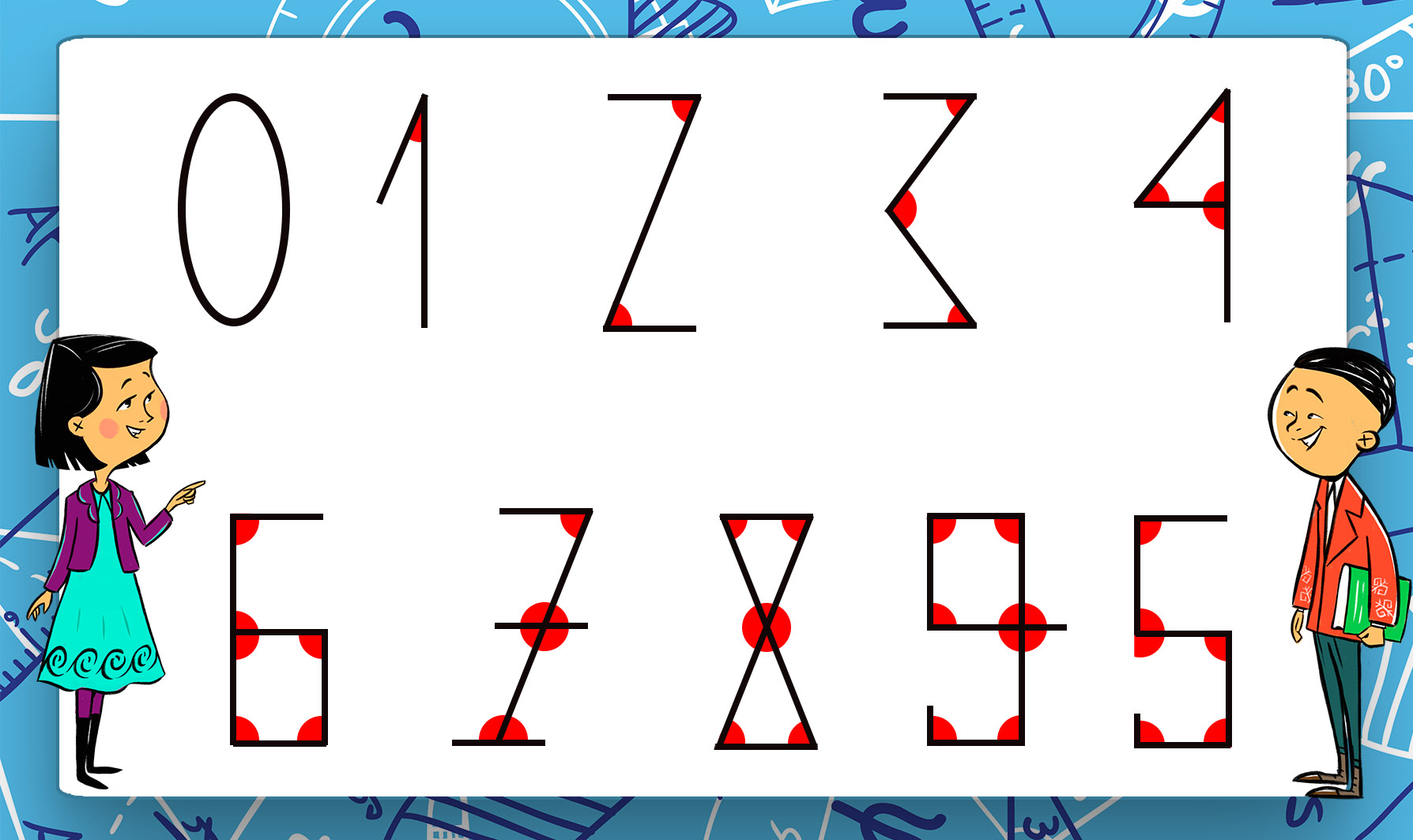БИЛИМ БУЛАГЫ

Математика: Действительные числа (Вещественные числа) — различия между версиями

 
(не показаны 2 промежуточные версии 2 участников)
Строка 3: Строка 3:
  
 
==История чисел==
 
==История чисел==
−
<div class="show-for-large-up">{{center|[[Файл:Числа_вокруг_нас.gif|500px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Числа_вокруг_нас.gif]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Числа_вокруг_нас.gif|400px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Числа_вокруг_нас.gif]]}}</div>
  
 
Современный мир  невозможно  представить без чисел. Они окружают нас повсюду. Мы сталкиваемся с ними каждый день, производим над ними десятки, сотни и тысячи действий с помощью различных технических средств. Мы так к этому привыкли, что история развития чисел нас совершенно не интересует, а многие об этом попросту никогда и не задумываются.  Но без знания прошлого никогда нельзя понять настоящее, а поэтому необходимо стремиться к постижению истоков. Так какова история развития чисел? Когда они появились, как человек дошел до их создания? Давайте же узнаем об этом!  
 
Современный мир  невозможно  представить без чисел. Они окружают нас повсюду. Мы сталкиваемся с ними каждый день, производим над ними десятки, сотни и тысячи действий с помощью различных технических средств. Мы так к этому привыкли, что история развития чисел нас совершенно не интересует, а многие об этом попросту никогда и не задумываются.  Но без знания прошлого никогда нельзя понять настоящее, а поэтому необходимо стремиться к постижению истоков. Так какова история развития чисел? Когда они появились, как человек дошел до их создания? Давайте же узнаем об этом!  
  
−
<div class="show-for-large-up">{{center|[[Файл:История_чисел.jpg|500px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:История_чисел.jpg]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:История_чисел.jpg|400px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:История_чисел.jpg]]}}</div>
  
−
<div class="show-for-large-up">{{left|[[Файл:Начала 5 книга Евклида Начала Теория отношений Евдокса 1.jpg|300px]]}}</div>
+
<div class="show-for-large-up">{{left|[[Файл:5_books_Evklid.jpg|300px]]}}</div>
−
<div class="hide-for-large-up">{{left|[[Файл:Начала 5 книга Евклида Начала Теория отношений Евдокса 1.jpg|200px]]}}</div>
+
<div class="hide-for-large-up">{{left|[[Файл:5_books_Evklid.jpg|200px]]}}</div>
  
 
Первая развитая числовая система, построенная в Древней Греции, включала только натуральные числа и их отношения. Однако вскоре выяснилось, что для целей геометрии и астрономии этого недостаточно: например, отношение длины диагонали квадрата к длине его стороны не может быть представлено ни натуральным, ни рациональным числом. Для выхода из положения Евдокс Книдский ввёл, в дополнение к числам, более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма. Теория Евдокса — это геометрическая модель вещественных чисел.  
 
Первая развитая числовая система, построенная в Древней Греции, включала только натуральные числа и их отношения. Однако вскоре выяснилось, что для целей геометрии и астрономии этого недостаточно: например, отношение длины диагонали квадрата к длине его стороны не может быть представлено ни натуральным, ни рациональным числом. Для выхода из положения Евдокс Книдский ввёл, в дополнение к числам, более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма. Теория Евдокса — это геометрическая модель вещественных чисел.  
Строка 20: Строка 20:
 
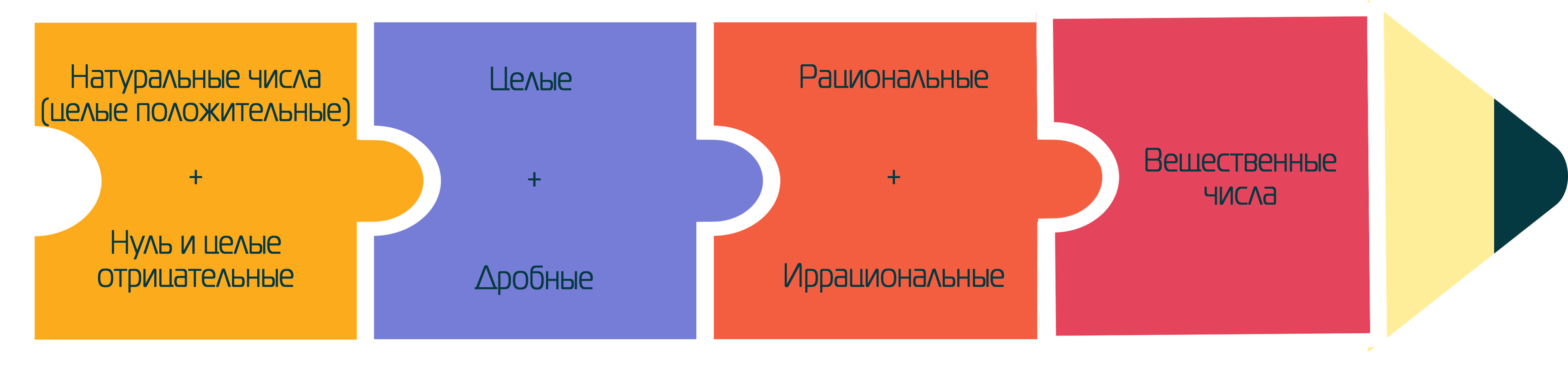
Историю развития понятия о числе можно изобразить в виде схемы:
 
Историю развития понятия о числе можно изобразить в виде схемы:
  
−
<div class="show-for-large-up">{{center|[[File:История чисел пазл.png|500px]]}}</div>
+
<div class="show-for-large-up">{{center|[[File:История чисел пазл.png]]}}</div>
−
<div class="hide-for-large-up">{{center|[[File:История чисел пазл.png|500px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[File:История чисел пазл.png]]}}</div>
  
 
==Понятие вещественного числа==
 
==Понятие вещественного числа==
Строка 29: Строка 29:
 
Наглядно вещественное число можно представить себе при помощи числовой прямой. Если на прямой указать положительное  направление, выбрать начальную точку и единичный отрезок, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой, и обратно, каждая точка будет представлять единственное  вещественное число. Поэтому термин «числовая прямая» обычно употребляется в качестве синонима множества вещественных чисел.  Множество вещественных чисел обозначают латинской буквой  R.
 
Наглядно вещественное число можно представить себе при помощи числовой прямой. Если на прямой указать положительное  направление, выбрать начальную точку и единичный отрезок, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой, и обратно, каждая точка будет представлять единственное  вещественное число. Поэтому термин «числовая прямая» обычно употребляется в качестве синонима множества вещественных чисел.  Множество вещественных чисел обозначают латинской буквой  R.
  
−
<div class="show-for-large-up">{{center|[[File:Числовая_прямая_м_.gif|500px]]}}</div>
+
<div class="show-for-large-up">{{center|[[File:Числовая_прямая_м_.gif]]}}</div>
−
<div class="hide-for-large-up">{{center|[[File:Числовая_прямая_м_.gif|500px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[File:Числовая_прямая_м_.gif]]}}</div>
  
 
Свойства арифметических действий над вещественными числами. Основные законы алгебры.
 
Свойства арифметических действий над вещественными числами. Основные законы алгебры.
Строка 45: Строка 45:
 
# a∙(b+c)=a∙b+a∙c.  
 
# a∙(b+c)=a∙b+a∙c.  
 
# a∙1=a.  
 
# a∙1=a.  
−
# a∙[[File:Дробь 1а.png|15px]]=1,a≠0.  
+
# a∙[[File:Drob_1a.png|15px]]=1,a≠0.  
  
 
Эти свойства называют основными законами алгебры.
 
Эти свойства называют основными законами алгебры.
Строка 68: Строка 68:
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
   <li class="active">
 
   <li class="active">
−
     [[file:Пример_1_Вещественные_числа.gif|300px]]
+
     [[file:Пример_1_Вещественные_числа.gif]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Пример 2 Вещественные числа.gif|300px]]
+
     [[file:Пример 2 Вещественные числа.gif]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Пример_3_Вещественные_числа.gif|300px]]
+
     [[file:Пример_3_Вещественные_числа.gif]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 134: Строка 134:
 
1. Изначально все арабские цифры состояли только из пересекающихся отрезков. Они были созданы по принципу «значение цифры соответствует количеству углов в ее написании». Например:ноль-ноль углов, единица-один угол, двойка-два угла и т.д.
 
1. Изначально все арабские цифры состояли только из пересекающихся отрезков. Они были созданы по принципу «значение цифры соответствует количеству углов в ее написании». Например:ноль-ноль углов, единица-один угол, двойка-два угла и т.д.
  
−
{{center|[[Файл:Арабские цифры в виде отрезков.jpg|400px]]}}
+
{{center|[[Файл:Арабские цифры в виде отрезков.jpg]]}}
  
 
2. Брахмагупта-индийский математик, который жил в VII веке первым начал использовать положительные и отрицательные числа. Однако,  до 13 века отрицательные числа практически не использовались, пока их не ввел в привычный оборот итальянский математик Леонардо Фибоначчи, чтобы фиксировать свои долги.
 
2. Брахмагупта-индийский математик, который жил в VII веке первым начал использовать положительные и отрицательные числа. Однако,  до 13 века отрицательные числа практически не использовались, пока их не ввел в привычный оборот итальянский математик Леонардо Фибоначчи, чтобы фиксировать свои долги.
Строка 140: Строка 140:
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
   <li class="active">
 
   <li class="active">
−
     [[file:Брамагупта.png|300px]]
+
     [[file:Брамагупта.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Леонардо_Фибоначчи.png|300px]]
+
     [[file:Леонардо_Фибоначчи.png]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 149: Строка 149:
 
3. В Американском штате  Индиана  действует закон: на территории штата число π следует считать равным '''4'''!
 
3. В Американском штате  Индиана  действует закон: на территории штата число π следует считать равным '''4'''!
  
−
{{center|[[Файл:Карта_США_._Названия_штатов.jpg|400px]]}}
+
{{center|[[Файл:Карта_США_._Названия_штатов.jpg]]}}
  
  
 
4. Многие представители научного общества называют число π математической константой, которая имеет свои секреты и потайные значения. Если посмотреть на ряд исследований, можно сказать, что ученые всех веков и народов уделяли множество времени этому числу, поэтому мы с легкостью смогли выбрать самые интересные факты о числе π.  
 
4. Многие представители научного общества называют число π математической константой, которая имеет свои секреты и потайные значения. Если посмотреть на ряд исследований, можно сказать, что ученые всех веков и народов уделяли множество времени этому числу, поэтому мы с легкостью смогли выбрать самые интересные факты о числе π.  
  
−
{{center|[[Файл:7_фактов_о_числе_Пи_–_интересные_особенности_и_математические_исследования.mp4|400px|start=1]]}}
+
{{center|[[Файл:7_faktov_pi.mp4|400px|start=1]]}}
  
 
</div>
 
</div>
Строка 167: Строка 167:
 
Дэвид Макдональд  переложил  число π на ноты с точностью до 122 знака после запятой. Механизм очень прост: каждой музыкальной ступени гаммы была присвоена цифра от 0 до 9. За основу была взята тональность ля-минор. И вот, число Пи превратилось в удивительно гармоничную и даже несколько «космическую» мелодию, исполнение которой сопровождается  интересными фактами о числе  π.
 
Дэвид Макдональд  переложил  число π на ноты с точностью до 122 знака после запятой. Механизм очень прост: каждой музыкальной ступени гаммы была присвоена цифра от 0 до 9. За основу была взята тональность ля-минор. И вот, число Пи превратилось в удивительно гармоничную и даже несколько «космическую» мелодию, исполнение которой сопровождается  интересными фактами о числе  π.
  
−
{{center|[[Файл:Музыка_числа_Пи.mp4|400px]]}}
+
{{center|[[Файл:Музыка_числа_Пи.mp4]]}}
  
 
</div>
 
</div>
Строка 193: Строка 193:
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
   <li class="active">
 
   <li class="active">
−
     [[file:Компьютерная_визуализвация.png|300px]]
+
     [[file:Компьютерная_визуализвация.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Компьютерная_визуализвация_Крживинского.png|300px]]
+
     [[file:Компьютерная_визуализвация_Крживинского.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
   [[file:Мозаика._Берлин._Германия.png|300px]]
+
   [[file:Мозаика._Берлин._Германия.png]]
 
   </li>
 
   </li>
 
<li>
 
<li>
−
   [[file:Памятник_в_Нью-Йорке.png|300px]]
+
   [[file:Памятник_в_Нью-Йорке.png]]
 
   </li>
 
   </li>
 
<li>
 
<li>
−
   [[file:Памятник числу Пи.Пермь Россия.png|300px]]
+
   [[file:Памятник числу Пи.Пермь Россия.png]]
 
   </li>
 
   </li>
 
<li>
 
<li>
−
   [[file:Визуалы_числа_Пи.png|300px]]
+
   [[file:Визуалы_числа_Пи.png]]
 
   </li>
 
   </li>
 
<li>
 
<li>
−
   [[file:Посевы_уложенные_числом_Пи.png|300px]]
+
   [[file:Посевы_уложенные_числом_Пи.png]]
 
   </li>
 
   </li>
 
<li>
 
<li>
−
   [[file:Река Нарын.png|300px]]
+
   [[file:Река Нарын.png]]
 
   </li>
 
   </li>
 
<li>
 
<li>
−
   [[file:Настенные_часы.png|300px]]
+
   [[file:Настенные_часы.png]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 257: Строка 257:
  
 
</div>
 
</div>
−
 
+
<div class="sbstyle">
 +
<div class="row">
 +
<div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Пройди тестирование</div>
 +
</div>
 +
 +
</div>
 
</div>
 
</div>
 
{{lang|:KR:Математика: Чыныгы сандар}}
 
{{lang|:KR:Математика: Чыныгы сандар}}
 
[[Category:Средняя школа]]
 
[[Category:Средняя школа]]
 
[[Category:Математика]]
 
[[Category:Математика]]

Текущая версия на 08:44, 22 октября 2018

История чисел

Числа вокруг нас.gif
Числа вокруг нас.gif

Современный мир невозможно представить без чисел. Они окружают нас повсюду. Мы сталкиваемся с ними каждый день, производим над ними десятки, сотни и тысячи действий с помощью различных технических средств. Мы так к этому привыкли, что история развития чисел нас совершенно не интересует, а многие об этом попросту никогда и не задумываются. Но без знания прошлого никогда нельзя понять настоящее, а поэтому необходимо стремиться к постижению истоков. Так какова история развития чисел? Когда они появились, как человек дошел до их создания? Давайте же узнаем об этом!

История чисел.jpg
История чисел.jpg
5 books Evklid.jpg
5 books Evklid.jpg

Первая развитая числовая система, построенная в Древней Греции, включала только натуральные числа и их отношения. Однако вскоре выяснилось, что для целей геометрии и астрономии этого недостаточно: например, отношение длины диагонали квадрата к длине его стороны не может быть представлено ни натуральным, ни рациональным числом. Для выхода из положения Евдокс Книдский ввёл, в дополнение к числам, более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма. Теория Евдокса — это геометрическая модель вещественных чисел.

Ситуация начала меняться в первые века нашей эры. Уже Диофант Александрийский, вопреки прежним традициям, рассматривает дроби так же, как и натуральные числа, а в IV книге своей «Арифметики» даже пишет об одном результате: «Число оказывается не рациональным». После гибели античной науки на передний план выдвинулись индийские и исламские математики, для которых любой результат измерения или вычисления считался числом. Эти взгляды постепенно взяли верх и в средневековой Европе, где поначалу разделяли рациональные и иррациональные числа называли мнимыми, абсурдными, глухими. Полное уравнивание в правах иррациональных чисел связано с трудами Симона Стевина в конце XVI века. А в 1707 году Исаак Ньютон в своей «Универсальной арифметике» даёт классическое определение вещественного числа, как отношение результата измерения к единичному эталону.

Историю развития понятия о числе можно изобразить в виде схемы:

История чисел пазл.png
История чисел пазл.png

Понятие вещественного числа

Вещественное, либо действительное число — математическая абстракция, которая возникла из необходимости в измерении геометрических и физических величин окружающего мира, кроме того, в проведении таких действий как извлечение корня, вычисление логарифмов, решение алгебраических уравнений.

Наглядно вещественное число можно представить себе при помощи числовой прямой. Если на прямой указать положительное направление, выбрать начальную точку и единичный отрезок, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой, и обратно, каждая точка будет представлять единственное вещественное число. Поэтому термин «числовая прямая» обычно употребляется в качестве синонима множества вещественных чисел. Множество вещественных чисел обозначают латинской буквой R.

Числовая прямая м .gif
Числовая прямая м .gif

Свойства арифметических действий над вещественными числами. Основные законы алгебры.

Над действительными числами можно выполнять арифметические действия. Они удовлетворяют тем же свойствам, что и действия над рациональными числами.


  1. a+b=b+a.
  2. (a+b)+c=a+(b+c).
  3. a+0=a .
  4. a+(-a)=0.
  5. a∙b=b∙a.
  6. (a∙b)∙c=a∙(b∙c).
  7. a∙(b+c)=a∙b+a∙c.
  8. a∙1=a.
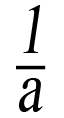  9. a∙Drob 1a.png=1,a≠0.

Эти свойства называют основными законами алгебры.

Свойства 1 и 5 выражают переместительный закон сложения и умножения соответственно;

Cвойства 2 и 6 выражают сочетательный закон;

Cвойство 7 — распределительный закон умножения относительно сложения;

Cвойства 3 и 8 указывают на наличие нейтрального элемента для сложения и умножения соответственно;

Cвойства 4 и 10 – на наличие нейтрализующего элемента соответственно.

Из этих свойств выделяются другие свойства. Например, a∙0=0. В самом деле, имеем:

a∙0=a∙(b+(-b))= a∙b+a∙(-b)= a∙b+(-a∙b)=0

В начало

Примеры

  • Пример 1 Вещественные числа.gif
  • Пример 2 Вещественные числа.gif
  • Пример 3 Вещественные числа.gif
В начало


Глоссарий

  • Положительные числа- числа, большее нуля.
  • Отрицательные числа- это числа со знаком минус (−), например −1, −2, −3 и т.д. Читается как: минус один, минус два, минус три и т.д.
  • Целые числа– это натуральные числа, число нуль, а также числа, противоположные натуральным.
  • Натуральные числа- это числа, которые используются для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов.
  • Рациональные числа-это числа, которые можно записать в виде положительной обыкновенной дроби, отрицательной обыкновенной дроби или числа нуль.
  • Иррациональные числа- числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби.
В начало

Полезные ссылки

  • Видеоурок на тему «Вещественные числа»: [Электронный ресурс] //Образование. Обучение - Znaika TV. Знайка.ру YouTube, 2018 https://www.youtube.com/watch?v=WrIXyM_rv-Y (Дата посещения: 14.04.2018)
  • Видеоурок на тему «Модуль действительного числа и его свойства» поможет сформировать понятие модуля.: [Электронный ресурс] // Люди и блоги YouTube, 2018 URL: https://www.youtube.com/watch?v=KbtNg7n9GpU (Дата посещения: 14.04.2018)
  • В книге Сергея Боброва «Волшебный двурог, или Правдивая история небывалых приключений нашего отважного друга Ильи Алексеевича Камова в неведомой стране» в занимательной форме рассказывается немало интересного для тех, кто любит точные науки и математику. Здесь вы узнаете о развитии математики, о ее значении в технике, а особенно об одной из важнейших отраслей математики - так называемом математическом анализе. На доступных примерах познакомитесь с элементами дифференциального и интегрального исчислений. Книгу можно использовать для самостоятельного изучения математики старшеклассникам школы или маленьким вундеркиндам.: [Электронный ресурс] // ЛитЛайф - литературный клуб URL: https://litlife.club/br/?b=282385 (Дата посещения: 14.04.2018)
В начало

Библиография

1. Гордый Рим трубил победу… Сергей Бобров.: [Электронный ресурс] // Antipodes Association Incorporated URL: http://www.antipodes.org.au/pr_pi_60.html (Дата посещения: 14.04.2018)

2. Совершенный Письмовник.: [Электронный ресурс] // Antipodes Association Incorporated URL: http://www.antipodes.org.au/pr_pi_all.html#Collection (Дата посещения: 14.04.2018)

3. Карл Эдуард Саган Контакт https: [Электронный ресурс] // ЛитЛайф - литературный клуб URL: https://litlife.club/br/?b=260441 (Дата посещения: 17.04.2018)

4. Сергей Бобров «Волшебный двурог, или Правдивая история небывалых приключений нашего отважного друга Ильи Алексеевича Камова в неведомой стране»: [Электронный ресурс] // ЛитЛайф - литературный клуб URL: https://litlife.club/br/?b=282385 (Дата посещения: 14.04.2018)

5. Факты о числе Пи.: [Электронный ресурс] // Удивительные факты для всех! 2013-2018 URL:http://amazing-facts.ru/science/fakty_o_chisle_pi.html (Дата посещения: 17.04.2018)

6. 10 удивительных визуализаций числа Пи: [Электронный ресурс] // DataReview.info URL: http://datareview.info/article/10-udivitelnyih-vizualizatsiy-chisla-pi/ (Дата посещения: 17.04.2018) 10 удивительных фактов о числе Пи: [Электронный ресурс] // 2013–2018 Пабли URL: http://www.publy.ru/post/25177 (Дата посещения: 17.04.2018)

7. Видеоурок на тему «Модуль действительного числа и его свойства»: [Электронный ресурс] // Люди и блоги YouTube, 2018 URL:https://www.youtube.com/watch?v=KbtNg7n9GpU (Дата посещения: 14.04.2018)

8. Видеоурок на тему «Вещественные числа» : [Электронный ресурс] //Образование. Обучение - Znaika TV. Знайка.ру YouTube, 2018 https://www.youtube.com/watch?v=WrIXyM_rv-Y (Дата посещения: 14.04.2018)

9. М. Я. Выгодский. Справочник по элементарной математике. Москва 1986.


В начало
Достоверные факты о числах

1. Изначально все арабские цифры состояли только из пересекающихся отрезков. Они были созданы по принципу «значение цифры соответствует количеству углов в ее написании». Например:ноль-ноль углов, единица-один угол, двойка-два угла и т.д.

Арабские цифры в виде отрезков.jpg

2. Брахмагупта-индийский математик, который жил в VII веке первым начал использовать положительные и отрицательные числа. Однако, до 13 века отрицательные числа практически не использовались, пока их не ввел в привычный оборот итальянский математик Леонардо Фибоначчи, чтобы фиксировать свои долги.

  • Брамагупта.png
  • Леонардо Фибоначчи.png

3. В Американском штате Индиана действует закон: на территории штата число π следует считать равным 4!

Карта США . Названия штатов.jpg


4. Многие представители научного общества называют число π математической константой, которая имеет свои секреты и потайные значения. Если посмотреть на ряд исследований, можно сказать, что ученые всех веков и народов уделяли множество времени этому числу, поэтому мы с легкостью смогли выбрать самые интересные факты о числе π.


Число π в музыке

Дэвид Макдональд переложил число π на ноты с точностью до 122 знака после запятой. Механизм очень прост: каждой музыкальной ступени гаммы была присвоена цифра от 0 до 9. За основу была взята тональность ля-минор. И вот, число Пи превратилось в удивительно гармоничную и даже несколько «космическую» мелодию, исполнение которой сопровождается интересными фактами о числе π.

Число π в искусстве

В научно-фантастическом романе «Контакт» американского астрофизика Карла Сагана учеными предпринимается попытка записать в двоичной системе число Пи. Так они приходят к выводу о существовании внеземного разума.

В 1998 году художественный фильм «Пи: Вера в хаос» режиссера Даррена Аронофски получил премию за лучшую режиссуру драматического фильма на кинофестивале Сандэнс. По сюжету, главный герой ищет простые ответы на вопросы, связанные с числом Пи, что сводит его с ума.

Визуализация числа π

Взглянув на то, как можно изобразить число π, понимаешь, насколько красива математика.

  • Компьютерная визуализвация.png
  • Компьютерная визуализвация Крживинского.png
  • Мозаика. Берлин. Германия.png
  • Памятник в Нью-Йорке.png
  • Памятник числу Пи.Пермь Россия.png
  • Визуалы числа Пи.png
  • Посевы уложенные числом Пи.png
  • Река Нарын.png
  • Настенные часы.png
Как запомнить число π

Этот вопрос терзает людей не одно столетие. Что только они не придумывали для его запоминания. Стихотворение про число π поможет сделать это быстрее.

Гордый Рим трубил победу

Над твердыней Сиракуз;

Но трудами Архимеда

Много больше я горжусь.

Надо нынче нам заняться,

Оказать старинке честь,

Чтобы нам не ошибаться,

Чтоб окружность верно счесть,

Надо только постараться

И запомнить все как есть

Три — четырнадцать —

пятнадцать — девяносто два и шесть! 

    Сергей Бобров
Пройди тестирование
Пройди тестирование
Источник — «https://bb.edu.gov.kg/index.php?title=Математика:_Действительные_числа_(Вещественные_числа)&oldid=27423»