БИЛИМ БУЛАГЫ

Математика: Координаты на плоскости — различия между версиями

(Отмена правки 18610, сделанной Admine2 (обсуждение))
 
(не показаны 4 промежуточные версии 2 участников)
Строка 1: Строка 1:
−
__NOTOC__
 
 
{{Якорь|Начало}}
 
{{Якорь|Начало}}
 
<div class="row  phis-bg"><div class="maintext large-8 medium-7 columns"><!-- Page Content -->
 
<div class="row  phis-bg"><div class="maintext large-8 medium-7 columns"><!-- Page Content -->
−
<div class="cutok">[[#История возникновения координат|История возникновения координат]] [[#Координаты на плоскости|Координаты на плоскости]]
 
−
[[#Координаты в нашей жизни|Координаты в нашей жизни]]</div>
 
  
 
==История возникновения координат==
 
==История возникновения координат==
Строка 15: Строка 12:
 
Проведем две перпендикулярные координатные прямые  x и y , которые пересекаются в начале отсчета — точке О. Эти прямые называют системой координат на плоскости, а точку О — началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
 
Проведем две перпендикулярные координатные прямые  x и y , которые пересекаются в начале отсчета — точке О. Эти прямые называют системой координат на плоскости, а точку О — началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
  
−
<div class="show-for-large-up">{{center|[[Файл:Координатная плоскость .mp4|400px|start=1]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Координатная плоскость .mp4|start=1]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Координатная плоскость .mp4|400px|start=1]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Координатная плоскость .mp4|start=1]]}}</div>
  
 
Пусть M - некоторая точка плоскости. Проведем через нее прямую MA, перпендикулярную координатной прямой x, и прямую MB перпендикулярную координатной прямой y. Так как точка A имеет координату 4, а точка B координату 3, то положение точки M  определяется парой чисел (4, 3). Эту пару чисел называют координатами точки M. Число 4 называют абсциссой точки M, а число 3 — ординатой точки M. Координатную прямую  x называют осью абсцисс, а координатную прямую  y — осью ординат. Точку М с абсциссой 4 и ординатой 3 обозначают так: M (4, 3). На первом месте пишут абсциссу точки, а на втором ее ординату. Если переставить координаты местами, то получится другая точка  N (3, 4), которая тоже изображена на рисунке.  
 
Пусть M - некоторая точка плоскости. Проведем через нее прямую MA, перпендикулярную координатной прямой x, и прямую MB перпендикулярную координатной прямой y. Так как точка A имеет координату 4, а точка B координату 3, то положение точки M  определяется парой чисел (4, 3). Эту пару чисел называют координатами точки M. Число 4 называют абсциссой точки M, а число 3 — ординатой точки M. Координатную прямую  x называют осью абсцисс, а координатную прямую  y — осью ординат. Точку М с абсциссой 4 и ординатой 3 обозначают так: M (4, 3). На первом месте пишут абсциссу точки, а на втором ее ординату. Если переставить координаты местами, то получится другая точка  N (3, 4), которая тоже изображена на рисунке.  
Строка 28: Строка 25:
 
Пример 1 . На координатной плоскости отметьте точки  А (1; 3), В (0;-4) , С (-3;-2)
 
Пример 1 . На координатной плоскости отметьте точки  А (1; 3), В (0;-4) , С (-3;-2)
  
−
<div class="show-for-large-up">{{center|[[Файл:Пример_1._Координаты_на_плоскости.mp4|400px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Пример_1._Координаты_на_плоскости.mp4]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Пример_1._Координаты_на_плоскости.mp4|400px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Пример_1._Координаты_на_плоскости.mp4]]}}</div>
  
 
Перпендикулярные прямые
 
Перпендикулярные прямые
Строка 37: Строка 34:
 
На рисунке  изображены прямые a и b, они перпендикулярны друг другу и осям координат. Пишут  a⊥b, a⊥Oy, b⊥Ox.  Если прямая a⊥b, то, b⊥a. Прямые  c  и  d перпендикулярны друг другу, но не перпендикулярны осям координат. Пишут  c⊥d.
 
На рисунке  изображены прямые a и b, они перпендикулярны друг другу и осям координат. Пишут  a⊥b, a⊥Oy, b⊥Ox.  Если прямая a⊥b, то, b⊥a. Прямые  c  и  d перпендикулярны друг другу, но не перпендикулярны осям координат. Пишут  c⊥d.
  
−
<div class="show-for-large-up">{{center|[[Файл:Перпендикулярные прямые. Координаты на плоскости.mp4|400px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Perpendik_pryamye.mp4]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Перпендикулярные прямые. Координаты на плоскости.mp4|400px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Perpendik_pryamye.mp4]]}}</div>
  
 
Параллельные прямые
 
Параллельные прямые
Строка 44: Строка 41:
 
Две различные прямые могут либо пересекаться в одной точке, либо не пересекаться. Две непересекающиеся прямые на плоскости называют параллельными.  Пишут AB∥MN. Эту запись читают так: «Прямая  AB параллельна прямой MN». Если  AB∥MN , то  MN∥AB.
 
Две различные прямые могут либо пересекаться в одной точке, либо не пересекаться. Две непересекающиеся прямые на плоскости называют параллельными.  Пишут AB∥MN. Эту запись читают так: «Прямая  AB параллельна прямой MN». Если  AB∥MN , то  MN∥AB.
  
−
<div class="show-for-large-up">{{center|[[Файл:Параллельные прямые. Координаты на плоскости .mp4|400px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Parallel_pryamye.mp4|400px]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Параллельные прямые. Координаты на плоскости .mp4|400px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Parallel_pryamye.mp4|400px]]}}</div>
  
 
Попробуйте самостоятельно решить эти задания. А верность ответов можно проверить с помощью видео, которое идет сразу после примеров.
 
Попробуйте самостоятельно решить эти задания. А верность ответов можно проверить с помощью видео, которое идет сразу после примеров.
Строка 55: Строка 52:
 
Пример 4. Даны точки  А (х; 2) и В (3; - 3).  Известно, что прямая АВ  перпендикулярна оси абсцисс. Найди значение х.
 
Пример 4. Даны точки  А (х; 2) и В (3; - 3).  Известно, что прямая АВ  перпендикулярна оси абсцисс. Найди значение х.
  
−
<div class="show-for-large-up">{{center|[[Файл:Паримеры_2,3,4._Координаты_на_плоскости_.mp4|400px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Primery2,3,4_pryamye.mp4|400px]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Паримеры_2,3,4._Координаты_на_плоскости_.mp4|400px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Primery2,3,4_pryamye.mp4|400px]]}}</div>
  
 
==Координаты в нашей жизни==
 
==Координаты в нашей жизни==
Строка 63: Строка 60:
 
Для начала воспользуемся набором приложений Google Карт, с помощью которых можно искать места по географическим координатам, а также определять координаты уже известных точек. Определим географические координаты города Бишкека.
 
Для начала воспользуемся набором приложений Google Карт, с помощью которых можно искать места по географическим координатам, а также определять координаты уже известных точек. Определим географические координаты города Бишкека.
  
−
<div class="show-for-large-up">{{center|[[Файл:Карта Гугол Бишкек.mp4|300px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Карта Гугол Бишкек.mp4]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Карта Гугол Бишкек.mp4|300px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Карта Гугол Бишкек.mp4]]}}</div>
  
 
А теперь выполним обратную операцию и узнаем, что скрывается за следующими координатами:  40°30'51.3"N 72°48'57.2"E.
 
А теперь выполним обратную операцию и узнаем, что скрывается за следующими координатами:  40°30'51.3"N 72°48'57.2"E.
  
−
<div class="show-for-large-up">{{center|[[Файл:Нахождение_по_координатам.mp4|300px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Нахождение_по_координатам.mp4]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Нахождение_по_координатам.mp4|300px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Нахождение_по_координатам.mp4]]}}</div>
  
 
Итак, зная координаты, легко найти расположение нужного объекта. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно. Например, чтобы пойти в гости к однокласснику, недостаточно знать только дом, в котором он живет, а нужно еще знать и номер квартиры. Верно проложить маршрут передвижения по городу можно с помощью веб-ГИС-технологии, записав в поисковике данного сервиса адрес начальной и конечной точки нашего путешествия.
 
Итак, зная координаты, легко найти расположение нужного объекта. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно. Например, чтобы пойти в гости к однокласснику, недостаточно знать только дом, в котором он живет, а нужно еще знать и номер квартиры. Верно проложить маршрут передвижения по городу можно с помощью веб-ГИС-технологии, записав в поисковике данного сервиса адрес начальной и конечной точки нашего путешествия.
  
−
<div class="show-for-large-up">{{center|[[Файл:Маршрут.png|300px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Маршрут.png]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Маршрут.png|300px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Маршрут.png]]}}</div>
  
 
В билете на поезд указан его номер и место назначения, а также номер вагона и посадочного места. В авиабилете мы также увидим номер рейса, модель самолёта, время вылета и прилёта. Чтобы найти свое место в зале театра или кинотеатра, сначала мы определяем нужный нам ряд, а затем уже свое место.  
 
В билете на поезд указан его номер и место назначения, а также номер вагона и посадочного места. В авиабилете мы также увидим номер рейса, модель самолёта, время вылета и прилёта. Чтобы найти свое место в зале театра или кинотеатра, сначала мы определяем нужный нам ряд, а затем уже свое место.  
Строка 80: Строка 77:
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
   <li class="active">
 
   <li class="active">
−
     [[file:Вокзал.png|300px]]
+
     [[file:Вокзал.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Расположение_мест_в_вагоне.png|300px]]
+
     [[file:Расположение_мест_в_вагоне.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Самолет.png|300px]]
+
     [[file:Самолет.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Расположение мест в самолете.jpg|300px]]
+
     [[file:Расположение мест в самолете.jpg]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Театр_Оперы_и_балета_имени_Малдыбаева.jpg|300px]]
+
     [[file:Театр_Оперы_и_балета_имени_Малдыбаева.jpg]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Театр_оперы_и_балета_зал.jpg|300px]]
+
     [[file:Театр_оперы_и_балета_зал.jpg]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 101: Строка 98:
 
Почти все хотя бы раз в жизни играли в «морской бой». Игроки скрывают друг от друга расположение своих судов и передают друг другу координаты в надежде  обнаружить вражеский корабль, расположение которого  определяется парой, состоящей из числа и буквы.  
 
Почти все хотя бы раз в жизни играли в «морской бой». Игроки скрывают друг от друга расположение своих судов и передают друг другу координаты в надежде  обнаружить вражеский корабль, расположение которого  определяется парой, состоящей из числа и буквы.  
  
−
<div class="show-for-large-up">{{center|[[Файл:Морской 1 бой.png|300px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Морской 1 бой.png]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Морской 1 бой.png|300px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Морской 1 бой.png]]}}</div>
  
 
В основе этого метода — создание сети с большим количеством ячеек и сопоставление этой сети длинного списка пар чисел. Именно таким образом мы получаем изображение на экране телевизора. Если взять часть этого изображения и последовательно ее увеличивать, то в результате можно увидеть квадраты. Каждый из этих маленьких квадратиков носит название «пиксель». Чтобы показать изображение, программа присваивает каждому квадратику-пикселю (то есть каждой паре чисел) определенный цвет. Чем больше количество пикселей на единицу площади, то есть чем более плотна применяемая нами сетка, тем лучше изображение.
 
В основе этого метода — создание сети с большим количеством ячеек и сопоставление этой сети длинного списка пар чисел. Именно таким образом мы получаем изображение на экране телевизора. Если взять часть этого изображения и последовательно ее увеличивать, то в результате можно увидеть квадраты. Каждый из этих маленьких квадратиков носит название «пиксель». Чтобы показать изображение, программа присваивает каждому квадратику-пикселю (то есть каждой паре чисел) определенный цвет. Чем больше количество пикселей на единицу площади, то есть чем более плотна применяемая нами сетка, тем лучше изображение.
  
−
<div class="show-for-large-up">{{center|[[Файл:Изображение_в_телевизоре.png|300px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Изображение_в_телевизоре.png]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Изображение_в_телевизоре.png|300px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Изображение_в_телевизоре.png]]}}</div>
  
 
Использование прямоугольных координат можно обнаружить и  в живописи. На одной из гравюр Дюрера изображён способ рисования с натуры через стекло с нанесённой на него квадратной сеткой. Если встать перед окном и, не изменяя точки зрения, обвести на стекле всё, что видно за ним, то полученный рисунок и будет перспективным изображением пространства.
 
Использование прямоугольных координат можно обнаружить и  в живописи. На одной из гравюр Дюрера изображён способ рисования с натуры через стекло с нанесённой на него квадратной сеткой. Если встать перед окном и, не изменяя точки зрения, обвести на стекле всё, что видно за ним, то полученный рисунок и будет перспективным изображением пространства.
  
−
<div class="show-for-large-up">{{center|[[Файл:Гравюра_Дюрера.jpg|300px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Гравюра_Дюрера.jpg]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Гравюра_Дюрера.jpg|300px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Гравюра_Дюрера.jpg]]}}</div>
  
  
Строка 170: Строка 167:
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
   <li class="active">
 
   <li class="active">
−
     [[file:Портреты ученых Гиппарх.jpg|300px]]
+
     [[file:Портреты ученых Гиппарх.jpg]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Портреты_ученых_Декарт.jpg|300px]]
+
     [[file:Портреты_ученых_Декарт.jpg]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Портреты_ученых_Лейбниц.jpg|300px]]
+
     [[file:Портреты_ученых_Лейбниц.jpg]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Портреты_ученых_Пьер_де_Ферма.jpg|300px]]
+
     [[file:Портреты_ученых_Пьер_де_Ферма.jpg]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Портреты_ученых_Эйлер.jpg|300px]]
+
     [[file:Портреты_ученых_Эйлер.jpg]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Портреты ученых Анаксима́ндр Миле́тский.jpg|300px]]
+
     [[file:Портреты ученых Анаксима́ндр Миле́тский.jpg]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 201: Строка 198:
 
Отметьте на координатной плоскости точки:  (0;-9), (0;-5), (0;-1), (0;2), (0;4), (0;9), (1;-3), (1;0), (1;2), (1;3), (1;4), (1;9), (2;-4), (2;-2), (2;3), (3;-10,5), (3;-9), (3;- 3), (3;0), (3;2), (3;5), (4;-7), (4;3), (4;4), (4;8), (5;-9), (5;-8), (5;-5), (5;-3), (5;1), (5;7), (5;8), (5;9), (6;-7), (6;3), (6;5), (6;8), (7;-8), (7;9), (8;-7), (8;8), (9;-8), (9;-6), (9;-3), (11,-7). Достройте фигуру, учитывая, что она симметрична относительно оси ординат.
 
Отметьте на координатной плоскости точки:  (0;-9), (0;-5), (0;-1), (0;2), (0;4), (0;9), (1;-3), (1;0), (1;2), (1;3), (1;4), (1;9), (2;-4), (2;-2), (2;3), (3;-10,5), (3;-9), (3;- 3), (3;0), (3;2), (3;5), (4;-7), (4;3), (4;4), (4;8), (5;-9), (5;-8), (5;-5), (5;-3), (5;1), (5;7), (5;8), (5;9), (6;-7), (6;3), (6;5), (6;8), (7;-8), (7;9), (8;-7), (8;8), (9;-8), (9;-6), (9;-3), (11,-7). Достройте фигуру, учитывая, что она симметрична относительно оси ординат.
  
−
{{center|[[Файл:Рисуем_по_точкам..mp4|400px]]}}
+
{{center|[[Файл:Рисуем_по_точкам..mp4]]}}
 
</div>
 
</div>
  
Строка 214: Строка 211:
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
   <li class="active">
 
   <li class="active">
−
     [[file:Применение_координат_в_авиации.png|300px]]
+
     [[file:Применение_координат_в_авиации.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_в_астрономии.png|300px]]
+
     [[file:Применение_координат_в_астрономии.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_в_биологии.png|300px]]
+
     [[file:Применение_координат_в_биологии.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_в_военном_деле.png|300px]]
+
     [[file:Применение_координат_в_военном_деле.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_в_географии.png|300px]]
+
     [[file:Применение_координат_в_географии.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_в_инженерной_графике.png|300px]]
+
     [[file:Применение_координат_в_инженерной_графике.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_в_медицине.png|300px]]
+
     [[file:Применение_координат_в_медицине.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_в_навигации.png|300px]]
+
     [[file:Применение_координат_в_навигации.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_в_строительстве.png|300px]]
+
     [[file:Применение_координат_в_строительстве.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_в_химии.png|300px]]
+
     [[file:Применение_координат_в_химии.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_компас.png|300px]]
+
     [[file:Применение_координат_компас.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
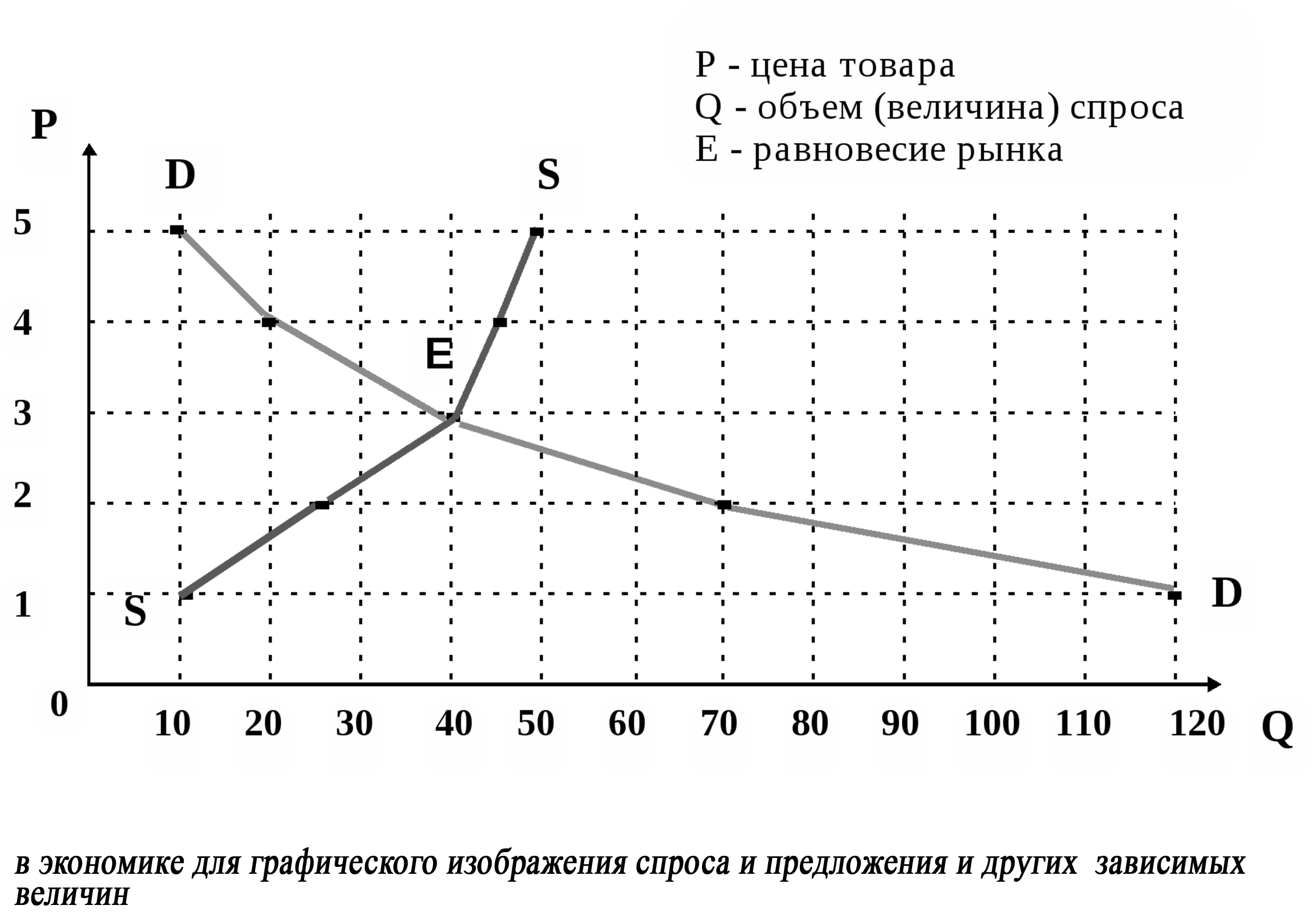
     [[file:Применение координат Кривая спроса.png|300px]]
+
     [[file:Применение координат Кривая спроса.png]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Применение_координат_туристические_карты.png|300px]]
+
     [[file:Применение_координат_туристические_карты.png]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 263: Строка 260:
 
Все встают из-за парт. На экране появляются координаты точек. Если точка принадлежит первой четверти, ребята должны потянуться. Если второй – наклониться вперед. Третьей – руки в стороны. Четвертой – сделать «восьмерку» сцепленными руками. Если точка находится на оси – хлопнуть в ладоши.
 
Все встают из-за парт. На экране появляются координаты точек. Если точка принадлежит первой четверти, ребята должны потянуться. Если второй – наклониться вперед. Третьей – руки в стороны. Четвертой – сделать «восьмерку» сцепленными руками. Если точка находится на оси – хлопнуть в ладоши.
  
−
{{center|[[Файл:Физкульт_минутка.mp4|400px|start=1]]}}
+
{{center|[[Файл:Физкульт_минутка.mp4|start=1]]}}
  
 
Небылица о случае, который произошел с Декартом и подсказал ему идею координат:
 
Небылица о случае, который произошел с Декартом и подсказал ему идею координат:
Строка 324: Строка 321:
 
Лев Генденштейн
 
Лев Генденштейн
  
−
 
+
</div>
 +
<div class="sbstyle">
 +
<div class="row">
 +
<div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Пройди тестирование</div>
 +
</div>
 +
 +
</div>
 
</div>
 
</div>
 
{{lang|:KR:Математика: Тегиздиктеги координаттар}}
 
{{lang|:KR:Математика: Тегиздиктеги координаттар}}
 
[[Category:Средняя школа]]
 
[[Category:Средняя школа]]
 
[[Category:Математика]]
 
[[Category:Математика]]

Текущая версия на 08:48, 22 октября 2018

История возникновения координат

История возникновения координат и формирование системы координат берет начало в древнем мире, благодаря развитию таких наук как астрономия, география, живопись. Древнегреческого ученого Анаксимандра Милетского (ок. 610-546 до н. э.) считают составителем первой географической карты. Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести хорошо известные теперь географические координаты: широту и долготу - и обозначить их числами. Идея изображать числа в виде точек, а точкам давать числовые обозначения зародилась в далекой древности. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта.

Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Говорят, эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650) – того самого, чьим именем названы прямоугольные координаты. Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль из-за отсутствия элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.

Вклад в развитие координатного метода внес также Пьер Ферма. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке. А вот термины «абсцисса», «ордината» и «координаты» были впервые введены Вильгельмом Лейбницем в семнадцатом веке.

Координаты на плоскости

Проведем две перпендикулярные координатные прямые x и y , которые пересекаются в начале отсчета — точке О. Эти прямые называют системой координат на плоскости, а точку О — началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.

Пусть M - некоторая точка плоскости. Проведем через нее прямую MA, перпендикулярную координатной прямой x, и прямую MB перпендикулярную координатной прямой y. Так как точка A имеет координату 4, а точка B координату 3, то положение точки M определяется парой чисел (4, 3). Эту пару чисел называют координатами точки M. Число 4 называют абсциссой точки M, а число 3 — ординатой точки M. Координатную прямую x называют осью абсцисс, а координатную прямую y — осью ординат. Точку М с абсциссой 4 и ординатой 3 обозначают так: M (4, 3). На первом месте пишут абсциссу точки, а на втором ее ординату. Если переставить координаты местами, то получится другая точка N (3, 4), которая тоже изображена на рисунке.

Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината, и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.

Оси координат разбивают плоскость на четыре части – четверти I, II, III, IV. В пределах одной четверти знаки обеих координат сохраняются. В первой четверти они положительны, во второй – абсцисса отрицательна, а ордината положительна, в третьей – абсцисса и ордината отрицательны ,а в четвертой – абсцисса положительна, а ордината отрицательна.

Точки оси х имеют равные нулю ординаты (у=0), а точки оси у – равные нулю абсциссы (х=0). Абсцисса и ордината начала координат равны нулю.

Пример 1 . На координатной плоскости отметьте точки А (1; 3), В (0;-4) , С (-3;-2)

Перпендикулярные прямые

Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.

На рисунке изображены прямые a и b, они перпендикулярны друг другу и осям координат. Пишут a⊥b, a⊥Oy, b⊥Ox. Если прямая a⊥b, то, b⊥a. Прямые c и d перпендикулярны друг другу, но не перпендикулярны осям координат. Пишут c⊥d.

Параллельные прямые

Две различные прямые могут либо пересекаться в одной точке, либо не пересекаться. Две непересекающиеся прямые на плоскости называют параллельными. Пишут AB∥MN. Эту запись читают так: «Прямая AB параллельна прямой MN». Если AB∥MN , то MN∥AB.

Попробуйте самостоятельно решить эти задания. А верность ответов можно проверить с помощью видео, которое идет сразу после примеров.

Пример 2. На координатной плоскости через точку А (-4; 3) проведена прямая, параллельная оси ординат, а через точку В (5; -2) проведена прямая, параллельная оси абсцисс. Отметь точку пересечения этих прямых.

Пример 3. Дан прямоугольник ABCD и координаты его вершин А (3; 4), В (-5; 4), С (-5; -3). Отметьте на координатной плоскости вершину D.

Пример 4. Даны точки А (х; 2) и В (3; - 3). Известно, что прямая АВ перпендикулярна оси абсцисс. Найди значение х.

Координаты в нашей жизни

Как могут ли пригодиться в повседневной жизни знания о координатной плоскости? И доводилось ли вам слышать такую фразу, как «оставьте свои координаты» или «по каким координатам вас можно найти»? И задумывались ли вы над тем, что могут обозначать эти выражения?

Для начала воспользуемся набором приложений Google Карт, с помощью которых можно искать места по географическим координатам, а также определять координаты уже известных точек. Определим географические координаты города Бишкека.

А теперь выполним обратную операцию и узнаем, что скрывается за следующими координатами: 40°30'51.3"N 72°48'57.2"E.

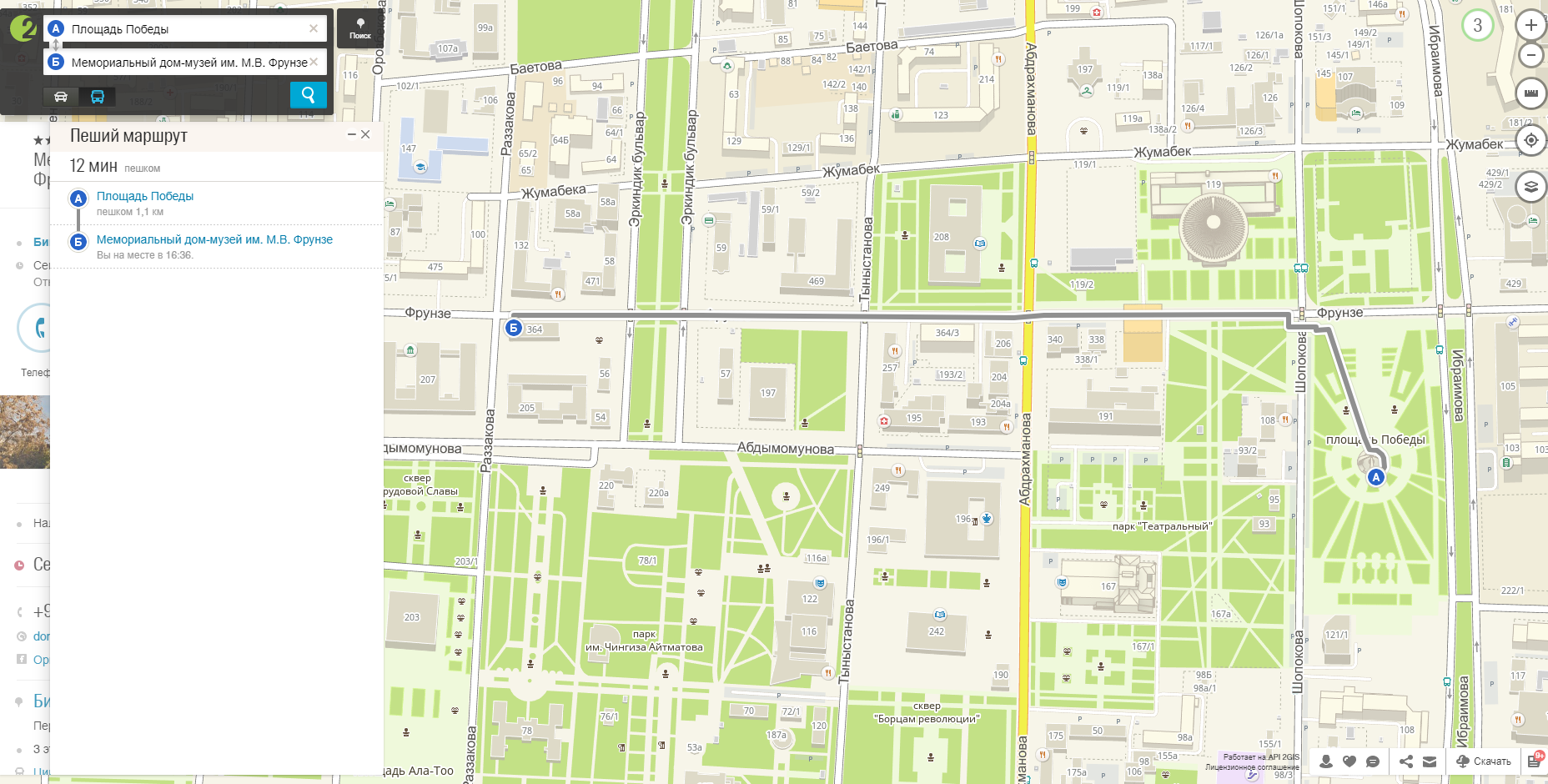
Итак, зная координаты, легко найти расположение нужного объекта. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно. Например, чтобы пойти в гости к однокласснику, недостаточно знать только дом, в котором он живет, а нужно еще знать и номер квартиры. Верно проложить маршрут передвижения по городу можно с помощью веб-ГИС-технологии, записав в поисковике данного сервиса адрес начальной и конечной точки нашего путешествия.

Маршрут.png
Маршрут.png

В билете на поезд указан его номер и место назначения, а также номер вагона и посадочного места. В авиабилете мы также увидим номер рейса, модель самолёта, время вылета и прилёта. Чтобы найти свое место в зале театра или кинотеатра, сначала мы определяем нужный нам ряд, а затем уже свое место.

  • Вокзал.png
  • Расположение мест в вагоне.png
  • Самолет.png
  • Расположение мест в самолете.jpg
  • Театр Оперы и балета имени Малдыбаева.jpg
  • Театр оперы и балета зал.jpg

Почти все хотя бы раз в жизни играли в «морской бой». Игроки скрывают друг от друга расположение своих судов и передают друг другу координаты в надежде обнаружить вражеский корабль, расположение которого определяется парой, состоящей из числа и буквы.

Морской 1 бой.png
Морской 1 бой.png

В основе этого метода — создание сети с большим количеством ячеек и сопоставление этой сети длинного списка пар чисел. Именно таким образом мы получаем изображение на экране телевизора. Если взять часть этого изображения и последовательно ее увеличивать, то в результате можно увидеть квадраты. Каждый из этих маленьких квадратиков носит название «пиксель». Чтобы показать изображение, программа присваивает каждому квадратику-пикселю (то есть каждой паре чисел) определенный цвет. Чем больше количество пикселей на единицу площади, то есть чем более плотна применяемая нами сетка, тем лучше изображение.

Изображение в телевизоре.png
Изображение в телевизоре.png

Использование прямоугольных координат можно обнаружить и в живописи. На одной из гравюр Дюрера изображён способ рисования с натуры через стекло с нанесённой на него квадратной сеткой. Если встать перед окном и, не изменяя точки зрения, обвести на стекле всё, что видно за ним, то полученный рисунок и будет перспективным изображением пространства.

Гравюра Дюрера.jpg
Гравюра Дюрера.jpg


В начало

Полезные ссылки

  • В книге Льва Генденштейна «Алиса в стране математики» вы снова встретитесь с персонажами всемирно известных сказок Льюиса Кэрролла. Вместе с Алисой вы сможете путешествовать по стране математики: решать увлекательные математические задачи, применяя свое творческое воображение и логическое мышление. В книге содержатся также исторические экскурсы, знакомящие с великими математиками и историей возникновения и развития математики с древности до наших дней. [Электронный ресурс] // ЛитЛайф - литературный клуб URL: https://litlife.club/br/?b=282306 (Дата посещения: 14.04.2018)
  • Увлекательная презентация "Система координат" в рамках IV регионального сетевого математического проекта "Системы координат: взгляд в прошлое и в настоящее".: [Электронный ресурс] // ООО CALAMEO URL: https://ru.calameo.com/read/001079152e4dd53000844 (дата обращения: 16. 04. 2018)
  • Если в системе координат разместить несколько точек, в определённом порядке, и соединить их, то получится фигура. А какие фигуры можно построить, смотрим здесь. Системы координат древности: [Электронный ресурс] // HintFox 2015 URL: http://www.hintfox.com/article/sistemi-koordinat-drevnosti.html (дата обращения: 16. 04. 2018)
В начало

Глоссарий

1. Числовая ось - прямая, на которой изображаются действительные числа

2. Абсцисса - лат. abscissa-отсекаемый (отрезок на оси иксов).

3. Ордината - лат. ordinatus – упорядоченный.

4. Координаты — величины, определяющие положение точки на плоскости .

5. Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

6. Симметрия — слово греческого происхождения, означает соразмерность, наличие определённого порядка, закономерности в расположении частей.

7. Веб-картография - это область компьютерных технологий связанная с доставкой пространственных данных конечному пользователю.

В начало

Библиография

В начало

Ученые, внесшие вклад в развитие координатного метода
  • Портреты ученых Гиппарх.jpg
  • Портреты ученых Декарт.jpg
  • Портреты ученых Лейбниц.jpg
  • Портреты ученых Пьер де Ферма.jpg
  • Портреты ученых Эйлер.jpg
  • Портреты ученых Анаксима́ндр Миле́тский.jpg


Рисуем по координатам

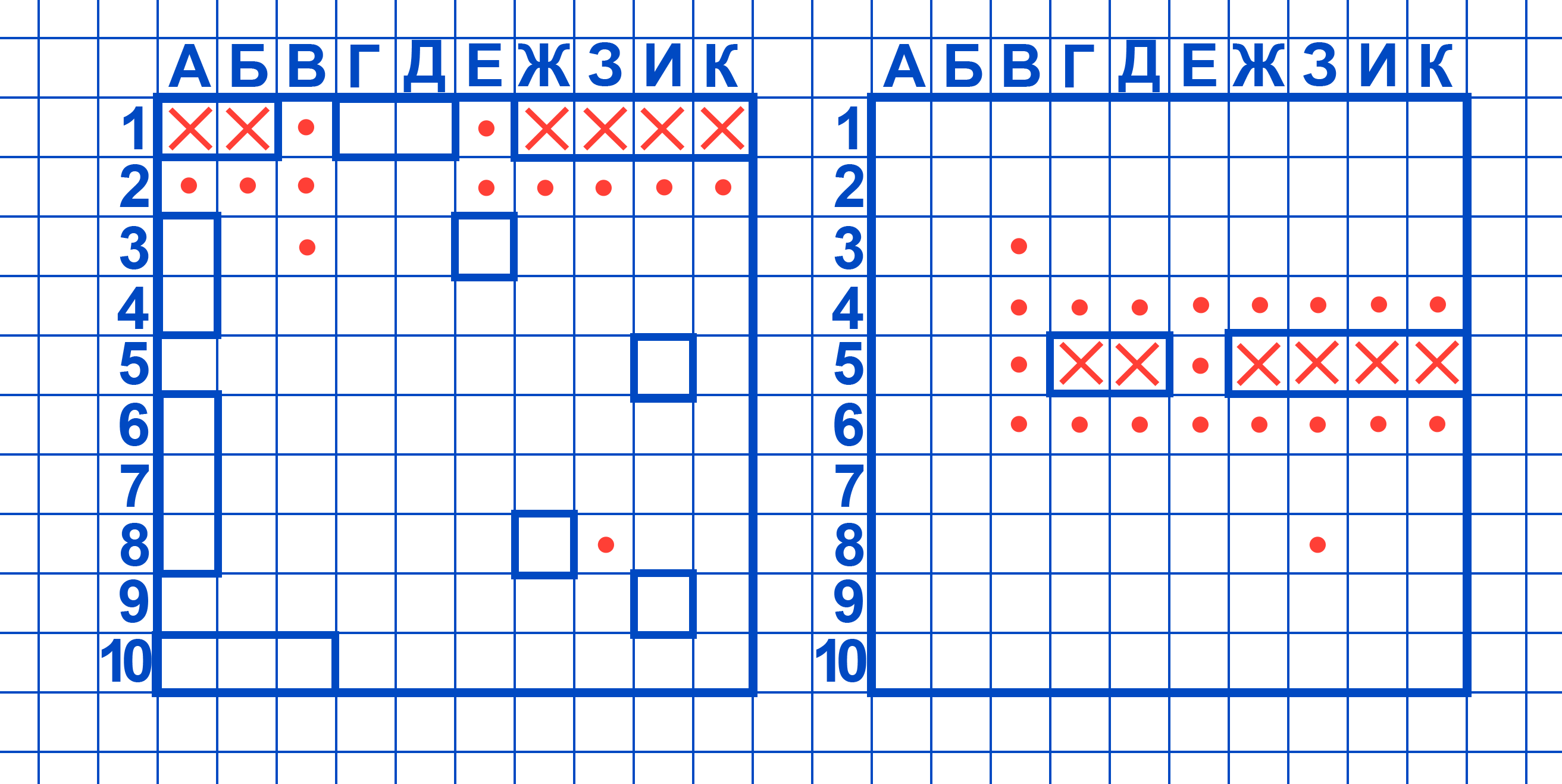
Суть задания заключается в том, чтобы по заданным координатам точек построить на координатной плоскости некоторое изображение. При этом построенные точки, как правило, последовательно соединяют плавной линией.

Отметьте на координатной плоскости точки: (0;-9), (0;-5), (0;-1), (0;2), (0;4), (0;9), (1;-3), (1;0), (1;2), (1;3), (1;4), (1;9), (2;-4), (2;-2), (2;3), (3;-10,5), (3;-9), (3;- 3), (3;0), (3;2), (3;5), (4;-7), (4;3), (4;4), (4;8), (5;-9), (5;-8), (5;-5), (5;-3), (5;1), (5;7), (5;8), (5;9), (6;-7), (6;3), (6;5), (6;8), (7;-8), (7;9), (8;-7), (8;8), (9;-8), (9;-6), (9;-3), (11,-7). Достройте фигуру, учитывая, что она симметрична относительно оси ординат.

Система координат в жизни

А еще систему координат применяют:

  • Применение координат в авиации.png
  • Применение координат в астрономии.png
  • Применение координат в биологии.png
  • Применение координат в военном деле.png
  • Применение координат в географии.png
  • Применение координат в инженерной графике.png
  • Применение координат в медицине.png
  • Применение координат в навигации.png
  • Применение координат в строительстве.png
  • Применение координат в химии.png
  • Применение координат компас.png
  • Применение координат Кривая спроса.png
  • Применение координат туристические карты.png
Математическая зарядка

Все встают из-за парт. На экране появляются координаты точек. Если точка принадлежит первой четверти, ребята должны потянуться. Если второй – наклониться вперед. Третьей – руки в стороны. Четвертой – сделать «восьмерку» сцепленными руками. Если точка находится на оси – хлопнуть в ладоши.

Небылица о случае, который произошел с Декартом и подсказал ему идею координат:

Однажды в незнакомый город

Приехал молодой Декарт.

Его ужасно мучил голод.

Стоял промозглый месяц март.

Решил к прохожей обратиться

Декарт, пытаясь, дрожь унять:

Где тут гостиница, скажите?

И дама стала объяснять:

– Идите до молочной лавки,

Потом до булочной, за ней

Цыганка продает булавки

И яд для крыс и для мышей,

А дальше будут магазины,

Найдете в них наверняка

Сыры, бисквиты, фрукты

И разноцветные шелка…

Все объяснения эти слушал

Декарт, от холода дрожа.

Ему хотелось очень кушать,

Но звонкий голос продолжал:

– За магазинами – аптека

(аптекарь там – усатый швед),

И церковь, где в начале века

Венчался, кажется, мой дед…

Когда на миг умолкла дама, Вдруг произнес ее слуга:

– Идите три квартала прямо

И два направо. Вход с угла.

Лев Генденштейн

Пройди тестирование
Пройди тестирование
Источник — «https://bb.edu.gov.kg/index.php?title=Математика:_Координаты_на_плоскости&oldid=27429»