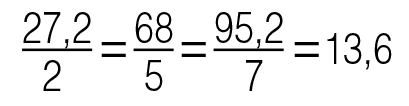Математика: Катыш жана пропорция — различия между версиями
Msu05 (обсуждение | вклад) |
Admine2 (обсуждение | вклад) |
||
| (не показано 17 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
<div class="row mat-bg"> | <div class="row mat-bg"> | ||
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> | <div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> | ||
{{Якорь|Башталышы}} | {{Якорь|Башталышы}} | ||
| − | |||
==Пропорция жөнүндө окуп-үйрөнүүнүн өнүгүү тарыхы== | ==Пропорция жөнүндө окуп-үйрөнүүнүн өнүгүү тарыхы== | ||
| Строка 15: | Строка 13: | ||
Кесиндини четки жана ортоңку катышынан кесүүдө келип чыккан пропорцияга карата алгачкы кызыгуулар антикалык илимдерде эле пайда болгон . | Кесиндини четки жана ортоңку катышынан кесүүдө келип чыккан пропорцияга карата алгачкы кызыгуулар антикалык илимдерде эле пайда болгон . | ||
| − | Байыркы Грецияда даңталган чыгармачылык искусствосунун, архитектурасынын, ар кандай кол өнөрчүлүктөрдүн доорунда өзгөчө ийгиликтүү өнүккөн. Пропорция менен сулуулукту даңазалоо, тартип жана гармония, музыкадагы үн коштоочу аккорддорду байланыштырышкан. Алтын бөлүнүш жөнүндө түшүнүгүн колдонууну | + | Байыркы Грецияда даңталган чыгармачылык искусствосунун, архитектурасынын, ар кандай кол өнөрчүлүктөрдүн доорунда өзгөчө ийгиликтүү өнүккөн. Пропорция менен сулуулукту даңазалоо, тартип жана гармония, музыкадагы үн коштоочу аккорддорду байланыштырышкан. Алтын бөлүнүш жөнүндө түшүнүгүн колдонууну байыркы грек философу жана математиги Пифагор киргизген. Ал жана анын окуучулары пропорциянын үч түрүн карашкан: |
* '''Арифметикалык: а - b = с - d''' | * '''Арифметикалык: а - b = с - d''' | ||
| Строка 25: | Строка 23: | ||
Башка байыркы грек окумуштуусу Платон пропорциянын маңызын мында: «эки жакты үчүнчү менен бириктирүү, аларды бир бүтүнгө «бекемдөө» үчүн пропорция керек. Мында бүтүндүн бир бөлүгү башкага бүтүндүн чоң бөлүгүнө мамиле кылгандай болуу керек. Мындай пропорция гармониялык биригүүгө жооп берет жана ал алтын болуп саналат». | Башка байыркы грек окумуштуусу Платон пропорциянын маңызын мында: «эки жакты үчүнчү менен бириктирүү, аларды бир бүтүнгө «бекемдөө» үчүн пропорция керек. Мында бүтүндүн бир бөлүгү башкага бүтүндүн чоң бөлүгүнө мамиле кылгандай болуу керек. Мындай пропорция гармониялык биригүүгө жооп берет жана ал алтын болуп саналат». | ||
| − | Байыркы грек окумуштуусу | + | Байыркы грек окумуштуусу Евдокс бүтүн сандарга гана эмес ошондой эле бөлчөк сандарга дагы колдонула турган пропорция жөнүндөгү систематикалык окууну берген. Катуу талаптуу пропорциянын теориясы биздин кылымга чейинки 3 кылымда байыркы грек геометриги Евклиддин белгилүү «Башталышында» берилген, ал 13 китептен турган. Бул теорияга ал 5 китепти арнаган. Евклид өзүнүн теориясынын негизин Евдокстун окууларынан алган. Азыркы убакта пропорциянын теориясы Евдокс – Евклиддин теорияларынан аз эле айырмаланат. Евклид пропорциялар арасындагы салыштырууну аныктаган: a : b катышы, c : d катышынан кичине, эгерде m жана n сандары болсо, эгерде ma > nb жана ошол эле убакта mc ≤ nd. А бул мындайча окулат: |
Бул факт таң калаарлык, анда «пропорция» сөзүн пайдаланууга байыркы рим коомдук ишмери МаркТу́ллийЦицеро́н киргизген. | Бул факт таң калаарлык, анда «пропорция» сөзүн пайдаланууга байыркы рим коомдук ишмери МаркТу́ллийЦицеро́н киргизген. | ||
Ал латынчага платон термини «аналогия» ны которгон, ал сөзмө-сөз «кайрадан -мамиле» дегенди билдирген, же биз азыр айтып жаткандай «катыш». | Ал латынчага платон термини «аналогия» ны которгон, ал сөзмө-сөз «кайрадан -мамиле» дегенди билдирген, же биз азыр айтып жаткандай «катыш». | ||
| − | |||
| − | |||
| − | |||
<div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | ||
==Негизги түшүнүктөр== | ==Негизги түшүнүктөр== | ||
| − | “Пропорция” сөзүн ( propotio латын сөзүнөн) которгондо “өлчөмдүүлүк, катыш”, “бөлүкчөлөрдүн өз ара аныкталган катышы” дегенди билдирген: [[Файл: | + | “Пропорция” сөзүн ( propotio латын сөзүнөн) которгондо “өлчөмдүүлүк, катыш”, “бөлүкчөлөрдүн өз ара аныкталган катышы” дегенди билдирген: [[Файл:proportion_a_b_cd.png|50px]] же a:b=c:d, бул жерде a,b,c,d – нолго барабар эмес, a жана d пропорциянын четки мүчөлөрү деп аталат, b жана c – пропорциянын ортоңку мүчөлөрү деп аталат'''. |
Мисалы 12 : 20 = 3 : 5. | Мисалы 12 : 20 = 3 : 5. | ||
| Строка 44: | Строка 39: | ||
Пропорциянын негизги касиеттери: пропорциянын акыркы мүчөлөрүнүн көбөйтүндүсү анын ортоңку мүчөлөрүнүн көбөйтүндүсүнө барабар. | Пропорциянын негизги касиеттери: пропорциянын акыркы мүчөлөрүнүн көбөйтүндүсү анын ортоңку мүчөлөрүнүн көбөйтүндүсүнө барабар. | ||
| − | Бул болсо,эгерде [[Файл: | + | Бул болсо,эгерде [[Файл:proportion_a_b_cd.png|50px]], анда ad = bc. |
| − | Карама-каршы ырастоо дагы туура: эгерде эки сандын көбөйтүндүсү a жана d эки башка сандын көбөйтүндүсүнө барабар болсо b жана c (a≠0,b≠0,c≠0,d≠0), анда бул сандар менен [[Файл: | + | Карама-каршы ырастоо дагы туура: эгерде эки сандын көбөйтүндүсү a жана d эки башка сандын көбөйтүндүсүнө барабар болсо b жана c (a≠0,b≠0,c≠0,d≠0), анда бул сандар менен [[Файл:proportion_a_b_cd.png|50px]] пропорциясын түзсөк болот. |
<div class="textblock">{{center|Пропорциянын негизги касиетинен келип чыгат, пропорциянын акыркы мүчөлөрү, пропорциянын акыркы белгилүү мүчөсүнө бөлүнгөн ортоңку мүчөлөрдүн көбөйтүндүсүнө барабар.}}</div> | <div class="textblock">{{center|Пропорциянын негизги касиетинен келип чыгат, пропорциянын акыркы мүчөлөрү, пропорциянын акыркы белгилүү мүчөсүнө бөлүнгөн ортоңку мүчөлөрдүн көбөйтүндүсүнө барабар.}}</div> | ||
| Строка 54: | Строка 49: | ||
'''1-тапшырма''' Пропорциянын белгисиз мүчөсүн тапкыла. | '''1-тапшырма''' Пропорциянын белгисиз мүчөсүн тапкыла. | ||
| − | '''2-тапшырма''' Китепканадагы 300 окурмандын | + | '''2-тапшырма''' Китепканадагы 300 окурмандын 108и - студенттер. Бардык окурмандардын канча процентин студенттер түзөт? |
'''3-тапшырма''' Кыям кайнатууда жемиш менен кумшекер 5:2 катышта колдонулат. Эгерде 450 грамм кумшекер алсак канча жемиш керек болот? | '''3-тапшырма''' Кыям кайнатууда жемиш менен кумшекер 5:2 катышта колдонулат. Эгерде 450 грамм кумшекер алсак канча жемиш керек болот? | ||
| Строка 73: | Строка 68: | ||
==Түз жана кыйыр пропорционалдуулук== | ==Түз жана кыйыр пропорционалдуулук== | ||
| − | <div class="textblock">{{center| | + | <div class="textblock">{{center|Эки өз ара көз каранды чоңдуктар эгерде, алардын чоңдуктары өзгөрүлбөй сакталса пропорционалдуу деп аталышат. Бул пропорционалдык чоңдуктардын туруктуу катышы пропорционалдуулуктун коэффициенти деп аталат. }}</div> |
| − | + | Мисал. Каалагандай буюмдун массасы анын көлөмүнө пропорционалдуу. Мисалы, 2 литр сымап 27,2 кг, 5 литр 68 кг, 7 литр 95,2 кг салмакта. Сымаптын массасы менен көлөмүнүн катышы (пропорционалдуулук коэффициенти) төмөнкүгө барабар: | |
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:plotnost_rtuti.png|200px]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:plotnost_rtuti.png|200px]]}}</div> |
| − | + | Бул учурда, пропорционалдуулук коэффициенти тыгыздуулугу болот. | |
| − | ''' | + | '''Пропорционалдуулук'''. Бул функционалдуулук көз карандуулуктун эң жөнөкөй түрү. Түз пропорционалдуулук менен (y = kx) тескери пропорционалдуулук ( y= k/x) айырмаланат. Мисалы, бир калыптагы v ылдамдыгындагы кыймылдын s жолу, t убактысына пропорционалдуу б.а. s = vt; аянты берилген тик бурчтуктун негизинин чоңдугуна түз пропорционалдуу, а x бийиктигине тескери пропорционалдуу б.а. y = a/ x. |
<div class="mw-customtoggle-ppol button17">'''Пропорционалдуулуктун касиеттери'''</div> | <div class="mw-customtoggle-ppol button17">'''Пропорционалдуулуктун касиеттери'''</div> | ||
| Строка 89: | Строка 84: | ||
'''Түз пропорционалдуу көз карандылыктын касиеттери.''' | '''Түз пропорционалдуу көз карандылыктын касиеттери.''' | ||
| − | 1. | + | '''1. х тин ар бир маанисине у тин жалгыз бир маанисинин дал келүүсү (түз пропорционалдуулуктун биринчи касиети).''' |
| − | 2. Түз пропорционалдуулук менен байланышы бар х жана у тин маалиреинин чоңдуктарынын тиешелүү катышы пропорционалдуулуктун коэффициентине барабар. | + | '''2. Түз пропорционалдуулук менен байланышы бар х жана у тин маалиреинин чоңдуктарынын тиешелүү катышы пропорционалдуулуктун коэффициентине барабар. |
| + | ''' | ||
| + | '''3. Эгерде түз пропорционалдуулук көз карандуулуктун эки чоңдугу өз ара байланышса, анда алардын бирөөсү чоңоюда (кичирейүүдө) башкасынын мааниси ошончого чоңоёт (кичирейет).''' | ||
| − | + | х жана у чоңдугунун түз пропорционалдуулуктун математикалык моделинин формуласы у = кх. | |
| − | |||
| − | |||
| − | |||
'''Тескери пропорционалдуулук көз карандылыктын касиеттери.''' | '''Тескери пропорционалдуулук көз карандылыктын касиеттери.''' | ||
| − | 1. | + | '''1. х тин ар бир маанисине (х=0дөн башка) у тин толук тиешелүү маанилери туура келет.''' |
| − | 2. | + | '''2. х жана у тин тиешелүү маанилерининин көбөйтүндүсүнө тескери пропорционалдуулуктун коэффициентине барабар.''' |
| − | 3. Эгерде х бир нече эсе чоңойсо (кичирейсе), анда ал экөөнүн көбөйтүндүсү өзгөрүүсүз калгандай болуп у тин мааниси ошончо эсеге кичирейет (чоңоёт). | + | '''3. Эгерде х бир нече эсе чоңойсо (кичирейсе), анда ал экөөнүн көбөйтүндүсү өзгөрүүсүз калгандай болуп у тин мааниси ошончо эсеге кичирейет (чоңоёт).''' |
Эгерде х менен у тескери пропорционалдуу көз каранды болсо, анда х тин каалагандай эки маанисинин чоңдуктары тиешелүү маанилердин тескери катышынын маанилерине барабар болот: x<sub>1</sub>:x<sub>2</sub>=y<sub>2</sub>:y<sub>1</sub>. | Эгерде х менен у тескери пропорционалдуу көз каранды болсо, анда х тин каалагандай эки маанисинин чоңдуктары тиешелүү маанилердин тескери катышынын маанилерине барабар болот: x<sub>1</sub>:x<sub>2</sub>=y<sub>2</sub>:y<sub>1</sub>. | ||
| Строка 112: | Строка 106: | ||
'''1-маселе''' Велосипедист туруктуу ылдамдык менен 10 минутада 5 км басып өткөн. 45 минутада канча жол басып өтөт? | '''1-маселе''' Велосипедист туруктуу ылдамдык менен 10 минутада 5 км басып өткөн. 45 минутада канча жол басып өтөт? | ||
| − | '''2-маселе''' | + | '''2-маселе''' Автоунаа 2 саатта ылдамдыгы 75 км/саат жүргөн. Эгерде ал ушул эле убакытта ылдамдыгы 90км/саат жүрсө канча аралыкты басып өтөт? |
<ul class="large-block-grid-2 small-block-grid-1"> | <ul class="large-block-grid-2 small-block-grid-1"> | ||
<li> | <li> | ||
| − | [[file:1-маселе.gif | + | [[file:1-маселе.gif]] |
</li> | </li> | ||
<li> | <li> | ||
| − | [[file:2_-маселе.gif | + | [[file:2_-маселе.gif]] |
</li> | </li> | ||
</ul> | </ul> | ||
| Строка 128: | Строка 122: | ||
==Алтын кесилиш== | ==Алтын кесилиш== | ||
| − | '''Геометрия эки кенге ээ: анын бири- Пифагордун теоремасы,''' | + | '''Геометрия эки кенге ээ: анын бири - Пифагордун теоремасы,''' |
'''экинчиси-кесиндилерди ортоңку жана акыркы катыштарга бөлүү...''' | '''экинчиси-кесиндилерди ортоңку жана акыркы катыштарга бөлүү...''' | ||
'''Биринчисин алтындын өлчөмү менен салыштырууга болот, а экинчиси баалуу ташка окшош. ''' | '''Биринчисин алтындын өлчөмү менен салыштырууга болот, а экинчиси баалуу ташка окшош. ''' | ||
| Строка 137: | Строка 131: | ||
'''Алтын кесилиш''' - бул кесиндини барабар эмес бөлүктөргө пропорционалдуу бөлүү, мында бүт кесинди чоң бөлүккө карайт, ал эми чоң бөлүктүн өзү кичинекейге карайт; же башкача айтканда, кичинекей кесинди ушундай эле чоңго карайт, чоң бардыгына карагандай: a : b = b : c же с : b = b : а. | '''Алтын кесилиш''' - бул кесиндини барабар эмес бөлүктөргө пропорционалдуу бөлүү, мында бүт кесинди чоң бөлүккө карайт, ал эми чоң бөлүктүн өзү кичинекейге карайт; же башкача айтканда, кичинекей кесинди ушундай эле чоңго карайт, чоң бардыгына карагандай: a : b = b : c же с : b = b : а. | ||
| − | <div class="show-for-large-up">{{center|[[Файл:Деление_отрезка.gif | + | <div class="show-for-large-up">{{center|[[Файл:Деление_отрезка.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Деление_отрезка.gif | + | <div class="hide-for-large-up">{{center|[[Файл:Деление_отрезка.gif]]}}</div> |
Алтын кесилиш менен практика жүзүндө таанышууну кесиндини түз алтын пропорцияда циркулдун жана сызгычтын жардамы менен бөлүүдөн башташат. | Алтын кесилиш менен практика жүзүндө таанышууну кесиндини түз алтын пропорцияда циркулдун жана сызгычтын жардамы менен бөлүүдөн башташат. | ||
| − | Алтын пропорциянын кесиндилери чексиз | + | Алтын пропорциянын кесиндилери чексиз иррационалдык бөлчөктөр менен туюнтулат AE = 0,618..., эгерде AB бирдик деп кабыл алсак, BE = 0,382... |
| − | Практикалык максатта көбүнчө жакындатылган мани 0,62 жана 0,38 ди пайдаланышат. Эгерде АВ кесиндисин 100 бөлүк деп кабыл алса, анда кесиндинин чоң бөлүгү 0,62 ге барабар, а кичинекей бөлүгү -38 бөлүккө. Алтын кесилиштин касиетин бул сандын айланасында түзүшкөн романтикалык сырдуулуктун ореолу жана араң эле мистикалык таазим этүү эмес. | + | Практикалык максатта көбүнчө жакындатылган мани 0,62 жана 0,38 ди пайдаланышат. Эгерде АВ кесиндисин 100 бөлүк деп кабыл алса, анда кесиндинин чоң бөлүгү 0,62 ге барабар, а кичинекей бөлүгү - 38 бөлүккө. Алтын кесилиштин касиетин бул сандын айланасында түзүшкөн романтикалык сырдуулуктун ореолу жана араң эле мистикалык таазим этүү эмес. |
| − | <div class="show-for-large-up">{{center|[[Файл:Деление_отрезка_прямой_по_золотому_сечению.gif | + | <div class="show-for-large-up">{{center|[[Файл:Деление_отрезка_прямой_по_золотому_сечению.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл:Деление_отрезка_прямой_по_золотому_сечению.gif | + | <div class="hide-for-large-up">{{center|[[Файл:Деление_отрезка_прямой_по_золотому_сечению.gif]]}}</div> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Пропорционалдуулук жаратылышта, искусстводо, архитектурада өсүмдүктүн, скульптуранын, имараттын туура жана көркөм предметтердин аныкталган өзүнчө өлчөмү ортосундагы катышты сактоону билдирет. | Пропорционалдуулук жаратылышта, искусстводо, архитектурада өсүмдүктүн, скульптуранын, имараттын туура жана көркөм предметтердин аныкталган өзүнчө өлчөмү ортосундагы катышты сактоону билдирет. | ||
| − | Алтын кесилиштин пропорциясына геометриялык фигура негизделет. Жактарынын ушундай катыштагы тик бурчтугу алтын тик бурчтук деген аталышка ээ болгон. | + | Алтын кесилиштин пропорциясына геометриялык фигура негизделет. Жактарынын ушундай катыштагы тик бурчтугу алтын тик бурчтук деген аталышка ээ болгон. Албетте, бул жерде алтын үч бурчтук да бар. Бул тең капталдуу үч бурчтук болот, мында каптал жактарынын узундугу негизинин узундугуна 1,618ге барабар болот. |
<div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | ||
| Строка 183: | Строка 153: | ||
Скрипканын добушу, анын үнүнүн сулуулугу кайсы бир өлчөмдө инструменттин формасынын алтын кесилиш пропорциясы менен келишиминен түз көз каранды. Музыкалык чыгармалардын Бахадан Шостаковичке чейинки диапозонунун анализи музыкалык формалардын негизги метрдик катыштарын жана ошондой эле алтын кесилишти көрсөткөн. Ошентип, гармония закону музыкалык тизмекте, Менделеевдин таблицасында, планеталар ортосундагы аралыкта, микро- жана макрокосмосто, илимдин көптөгөн тармактарында табылган. Скульптура, архитектура, астрономия, биология, техника, психология, ж.б.- бардык жактарда алтын кесилиш өзүн көрсөтүүдө. | Скрипканын добушу, анын үнүнүн сулуулугу кайсы бир өлчөмдө инструменттин формасынын алтын кесилиш пропорциясы менен келишиминен түз көз каранды. Музыкалык чыгармалардын Бахадан Шостаковичке чейинки диапозонунун анализи музыкалык формалардын негизги метрдик катыштарын жана ошондой эле алтын кесилишти көрсөткөн. Ошентип, гармония закону музыкалык тизмекте, Менделеевдин таблицасында, планеталар ортосундагы аралыкта, микро- жана макрокосмосто, илимдин көптөгөн тармактарында табылган. Скульптура, архитектура, астрономия, биология, техника, психология, ж.б.- бардык жактарда алтын кесилиш өзүн көрсөтүүдө. | ||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:Пропорция_бизди_курчап_турган_чөйрөдө.mp4]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Пропорция_бизди_курчап_турган_чөйрөдө.mp4]]}}</div> |
<div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Башталышы|Башталышына]]</div><br clear=all /> | ||
| Строка 226: | Строка 196: | ||
<!-- Sidebar --> | <!-- Sidebar --> | ||
<div class="large-4 medium-5 columns"> | <div class="large-4 medium-5 columns"> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<!-- четвертый элемент сайдбара лайфхак --> | <!-- четвертый элемент сайдбара лайфхак --> | ||
| Строка 336: | Строка 266: | ||
</div> | </div> | ||
| + | <!-- четвертый элемент сайдбара лайфхак --> | ||
| + | <div class="shadow radius sbstyle" style="margin-top:20px;"> | ||
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Архитектурадагы алтын кесилиш</div> | ||
| + | </div> | ||
| + | Пифагор алтын бөлүү билимин египеттиктер менен вавилондуктардан алган деген божомол бар. Чындыгында эле Хеопс пирамидасы, храмдар, барельефтери, турмуштагы предметтер жана Тутанхамон көрүстөнүндөгү жасалгалар египеттик чеберлердин аларды түзүүдө алтын кесилиш катышын пайдалангандары күбө болуп турат. Француз архитектору Шарль Эдуард Ле Корбюзье Абидостогу Сети I фараонунун ибадатканасынын рельефинен жана Рамзес фараонунун сүрөттөлүшүндө фигуралардын пропорциясы алтын бөлүү чоңдугуна дал келээрин тапкан. Хесира көрүстөнүндөгү жыгач тактага түзүрүлгөн Зодчийдин рельефинде, колунда алтын бөлүү пропорциясын бекитүүчү ченөө инструменттерин кармап турат. Гректер акылдуу геометрлар болушкан. Алар балдарына арифметиканы дагы геометриялык фигуралардын жардамы менен окутушкан. Пифагордун квадраты жана ал квадраттын диагоналы динамикалык тик бурчтукту түзүү үчүн негиз болгон. | ||
| + | |||
| + | Байыркы грек Парфенон храмынын фасадында алтын пропорция бар. Аны касууда байыркы (антикалык) дүйнөнүн архитекторлору жана скульпторлору пайдаланган циркульдар табылган. Помпеядагы колдонулган циркульга дагы алтын бөлүү пропорциясы мүнөздүү. Алтын кесилиш терминин Леонардо да Винчи (1452-1519-жж) киргизген. | ||
| + | |||
| + | <ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | ||
| + | <li class="active"> | ||
| + | {{center-p|[[file:Шарль_Эдуард_Ле_Корбюзье.jpg|Шарль Эдуард Ле Корбюзье]]|Шарль Эдуард Ле Корбюзье}} | ||
| + | </li> | ||
| + | <li> | ||
| + | {{center-p|[[file:Храм_фараона_Сети_I.jpg|Храм_фараона_Сети_I]]|Храм_фараона_Сети_I}} | ||
| + | </li> | ||
| + | <li> | ||
| + | {{center-p|[[file:Фараон_Сети_I_и_бог_Анубис._Рельеф_из_храма_Сети_I_в_Абидосе.jpg|Фараон_Сети_I_и_бог_Анубис._Рельеф_из_храма_Сети_I_в_Абидосе]]|Фараон_Сети_I_и_бог_Анубис._Рельеф_из_храма_Сети_I_в_Абидосе}} | ||
| + | </li> | ||
| + | <li> | ||
| + | {{center-p|[[file:Зодчий_на_рельефе_гробницы_Хесира.jpg|Зодчий_на_рельефе_гробницы_Хесира]]|Зодчий_на_рельефе_гробницы_Хесира}} | ||
| + | </li> | ||
| + | <li> | ||
| + | {{center-p|[[file:Парфенон.jpg|Парфенон]]|Парфенон}} | ||
| + | </li> | ||
| + | <li> | ||
| + | {{center-p|[[file:Античный_циркуль.jpg|Античный_циркуль]]|Античный_циркуль}} | ||
| + | </li> | ||
| + | </ul> | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <!-- Первый элемент сайдбара Это интересно или топ5/10/15 --> | ||
| + | <div class="shadow radius sbstyle"> | ||
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Өзүң үчүн “Алтын үйдү” кандай курса болот?</div> | ||
| + | </div> | ||
| + | |||
| + | {{center-p|[[Файл:Золотой_Храм_в_Амритсаре._Индия.jpg|Золотой Храм в Амритсаре. Индия]]|Золотой Храм в Амритсаре. Индия}} | ||
| + | |||
| + | Үй ичиндеги энергияны туура бөлүштүрүү, экология менен коопсуз курулуш материалдарын шайкеш келтирүү гармониялык конструкциясы азыркы архитекторлор менен дизайнерлерге “Алтын кесилишти” түшүнүүгө жана анын принциптерин пайдаланууга түрткү болот. Бул сметаны көбөйтөт жана проектинин тереңдеп иштөө таасирин түзөт. Баасы 60-80% өсөт. | ||
| + | |||
| + | Таланттуу сүрөтчүлөр жана архитекторлор үчүн чыгармачылык процесс маалында туюу (интуитивно) эрежеси сакталат. Бирок алардын кээ бирлери бул абалды акылы менен ишке ашырат. | ||
| + | |||
| + | Белгилүү француз архитектору Шарль Эдуард Ле Корбюзье келечектеги үйдүн жана интерьердин параметрлерин эсептөө үчүн баштапкы бирдик катары кожоюндун боюн алган. Анын бардык иштери чындыгында индивидуалдуу жана гармониялуу. | ||
| + | |||
| + | <ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" > | ||
| + | <li class="active"> | ||
| + | {{center-p| [[file:Здание_Ассамблеи_в_Чандигархе._Индия.jpg|Здание Ассамблеи в Чандигархе. Индия]]|Здание Ассамблеи в Чандигархе. Индия}} | ||
| + | </li> | ||
| + | <li> | ||
| + | {{center-p| [[file:Фото_1__Здание_Ассамблеи_в_Чандигархе._Индия1.jpg|Здание Ассамблеи в Чандигархе. Индия]]|Здание Ассамблеи в Чандигархе. Индия}} | ||
| + | </li> | ||
| + | <li> | ||
| + | {{center-p| [[file:Фото_Здание_Ассамблеи_в_Чандигархе._Индия2.jpg|Здание Ассамблеи в Чандигархе. Индия]]|Здание Ассамблеи в Чандигархе. Индия}} | ||
| + | </li> | ||
| + | </ul> | ||
| + | |||
| + | Катыштарды эсепке албастан салынган үйлөрдө, пропорцияга дал келиши үчүн бөлмөлөрдү кайрадан пландоого болот. Бул үчүн эмеректи кайрадан коюштуруу же кошумча тосмо жасоо эле жетиштүү. Терезе, эшиктердин узундугу менен туурасы аналогиялык мүнөздө өзгөрөт. | ||
| + | |||
| + | {{center-p|[[Файл:Шкаф-перегородка.jpg|Шкаф-перегородка]]|Шкаф-перегородка}} | ||
| + | |||
| + | Түс менен жасалгалоо кылууда жөнөкөйлөтүлгөн катышты алуу 60% негизги түс, 30%- ыраң, а калган 10% - тондорду өздөштүрүүнү күчөтүүчү эсепке жетет. | ||
| + | |||
| + | {{center-p|[[Файл:Вариант_освещения_комнаты.jpg|Вариант освещения комнаты]]|Вариант освещения комнаты}} | ||
| + | |||
| + | Эмеректин узундугу жана бийиктиги шыптын бийиктиги жана дубалдардын туурасы менен эсептелиши керек. | ||
| + | |||
| + | Интерьердеги бул нормалардын тиркемеси, архитектуралык оформленген тегиздик катары, өз алдынча уюштуруу, рекурсия, асимметрия, кооздук түшүнүктөрүн бириктирет. | ||
| + | |||
| + | </div> | ||
| + | |||
| + | |||
| + | |||
<!-- четвертый элемент сайдбара лайфхак --> | <!-- четвертый элемент сайдбара лайфхак --> | ||
| Строка 351: | Строка 355: | ||
| + | </div> | ||
| + | <div class="sbstyle"> | ||
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Тестти өтүңүз</div> | ||
| + | </div> | ||
| + | |||
</div> | </div> | ||
{{lang|Математика: Отношения и пропорции}} | {{lang|Математика: Отношения и пропорции}} | ||
Текущая версия на 08:57, 22 октября 2018
Содержание
Пропорция жөнүндө окуп-үйрөнүүнүн өнүгүү тарыхы
Сулуулуктан бөлөк эч нерсе жакпайт, а сулуулукта- эч нерсе, формадан бөлөк, формада- эч нерсе,
пропорциядан бөлөк, пропорцияда эч нерсе, сандардан бөлөк.
Аврелий Августин
Кесиндини четки жана ортоңку катышынан кесүүдө келип чыккан пропорцияга карата алгачкы кызыгуулар антикалык илимдерде эле пайда болгон .
Байыркы Грецияда даңталган чыгармачылык искусствосунун, архитектурасынын, ар кандай кол өнөрчүлүктөрдүн доорунда өзгөчө ийгиликтүү өнүккөн. Пропорция менен сулуулукту даңазалоо, тартип жана гармония, музыкадагы үн коштоочу аккорддорду байланыштырышкан. Алтын бөлүнүш жөнүндө түшүнүгүн колдонууну байыркы грек философу жана математиги Пифагор киргизген. Ал жана анын окуучулары пропорциянын үч түрүн карашкан:
- Арифметикалык: а - b = с - d
- Геометрикалык: a : b = c : d
- Гармоникалык: a : b = b : (a - b)
Башка байыркы грек окумуштуусу Платон пропорциянын маңызын мында: «эки жакты үчүнчү менен бириктирүү, аларды бир бүтүнгө «бекемдөө» үчүн пропорция керек. Мында бүтүндүн бир бөлүгү башкага бүтүндүн чоң бөлүгүнө мамиле кылгандай болуу керек. Мындай пропорция гармониялык биригүүгө жооп берет жана ал алтын болуп саналат».
Байыркы грек окумуштуусу Евдокс бүтүн сандарга гана эмес ошондой эле бөлчөк сандарга дагы колдонула турган пропорция жөнүндөгү систематикалык окууну берген. Катуу талаптуу пропорциянын теориясы биздин кылымга чейинки 3 кылымда байыркы грек геометриги Евклиддин белгилүү «Башталышында» берилген, ал 13 китептен турган. Бул теорияга ал 5 китепти арнаган. Евклид өзүнүн теориясынын негизин Евдокстун окууларынан алган. Азыркы убакта пропорциянын теориясы Евдокс – Евклиддин теорияларынан аз эле айырмаланат. Евклид пропорциялар арасындагы салыштырууну аныктаган: a : b катышы, c : d катышынан кичине, эгерде m жана n сандары болсо, эгерде ma > nb жана ошол эле убакта mc ≤ nd. А бул мындайча окулат: Бул факт таң калаарлык, анда «пропорция» сөзүн пайдаланууга байыркы рим коомдук ишмери МаркТу́ллийЦицеро́н киргизген.
Ал латынчага платон термини «аналогия» ны которгон, ал сөзмө-сөз «кайрадан -мамиле» дегенди билдирген, же биз азыр айтып жаткандай «катыш».
Негизги түшүнүктөр
“Пропорция” сөзүн ( propotio латын сөзүнөн) которгондо “өлчөмдүүлүк, катыш”, “бөлүкчөлөрдүн өз ара аныкталган катышы” дегенди билдирген: ![]() же a:b=c:d, бул жерде a,b,c,d – нолго барабар эмес, a жана d пропорциянын четки мүчөлөрү деп аталат, b жана c – пропорциянын ортоңку мүчөлөрү деп аталат.
же a:b=c:d, бул жерде a,b,c,d – нолго барабар эмес, a жана d пропорциянын четки мүчөлөрү деп аталат, b жана c – пропорциянын ортоңку мүчөлөрү деп аталат.
Мисалы 12 : 20 = 3 : 5.
Бул пропорция, акыркы мүчөлөрү 12 жана 5 ке барабар, ортоңку мүчөлөрү 20 жана 3. Пропорция мындайча окулат: он эки жыйырмага карайт, үч бешке карагандай.
Пропорциянын негизги касиеттери: пропорциянын акыркы мүчөлөрүнүн көбөйтүндүсү анын ортоңку мүчөлөрүнүн көбөйтүндүсүнө барабар.
Бул болсо,эгерде ![]() , анда ad = bc.
, анда ad = bc.
Карама-каршы ырастоо дагы туура: эгерде эки сандын көбөйтүндүсү a жана d эки башка сандын көбөйтүндүсүнө барабар болсо b жана c (a≠0,b≠0,c≠0,d≠0), анда бул сандар менен ![]() пропорциясын түзсөк болот.
пропорциясын түзсөк болот.
Пропорцияга мисалдар жана тапшырмалар
1-тапшырма Пропорциянын белгисиз мүчөсүн тапкыла.
2-тапшырма Китепканадагы 300 окурмандын 108и - студенттер. Бардык окурмандардын канча процентин студенттер түзөт?
3-тапшырма Кыям кайнатууда жемиш менен кумшекер 5:2 катышта колдонулат. Эгерде 450 грамм кумшекер алсак канча жемиш керек болот?
Түз жана кыйыр пропорционалдуулук
Мисал. Каалагандай буюмдун массасы анын көлөмүнө пропорционалдуу. Мисалы, 2 литр сымап 27,2 кг, 5 литр 68 кг, 7 литр 95,2 кг салмакта. Сымаптын массасы менен көлөмүнүн катышы (пропорционалдуулук коэффициенти) төмөнкүгө барабар:
Бул учурда, пропорционалдуулук коэффициенти тыгыздуулугу болот.
Пропорционалдуулук. Бул функционалдуулук көз карандуулуктун эң жөнөкөй түрү. Түз пропорционалдуулук менен (y = kx) тескери пропорционалдуулук ( y= k/x) айырмаланат. Мисалы, бир калыптагы v ылдамдыгындагы кыймылдын s жолу, t убактысына пропорционалдуу б.а. s = vt; аянты берилген тик бурчтуктун негизинин чоңдугуна түз пропорционалдуу, а x бийиктигине тескери пропорционалдуу б.а. y = a/ x.
Түз пропорционалдуу көз карандылыктын касиеттери.
1. х тин ар бир маанисине у тин жалгыз бир маанисинин дал келүүсү (түз пропорционалдуулуктун биринчи касиети).
2. Түз пропорционалдуулук менен байланышы бар х жана у тин маалиреинин чоңдуктарынын тиешелүү катышы пропорционалдуулуктун коэффициентине барабар. 3. Эгерде түз пропорционалдуулук көз карандуулуктун эки чоңдугу өз ара байланышса, анда алардын бирөөсү чоңоюда (кичирейүүдө) башкасынын мааниси ошончого чоңоёт (кичирейет).
х жана у чоңдугунун түз пропорционалдуулуктун математикалык моделинин формуласы у = кх.
Тескери пропорционалдуулук көз карандылыктын касиеттери.
1. х тин ар бир маанисине (х=0дөн башка) у тин толук тиешелүү маанилери туура келет.
2. х жана у тин тиешелүү маанилерининин көбөйтүндүсүнө тескери пропорционалдуулуктун коэффициентине барабар.
3. Эгерде х бир нече эсе чоңойсо (кичирейсе), анда ал экөөнүн көбөйтүндүсү өзгөрүүсүз калгандай болуп у тин мааниси ошончо эсеге кичирейет (чоңоёт).
Эгерде х менен у тескери пропорционалдуу көз каранды болсо, анда х тин каалагандай эки маанисинин чоңдуктары тиешелүү маанилердин тескери катышынын маанилерине барабар болот: x1:x2=y2:y1.
Маселени чыгаруу
1-маселе Велосипедист туруктуу ылдамдык менен 10 минутада 5 км басып өткөн. 45 минутада канча жол басып өтөт?
2-маселе Автоунаа 2 саатта ылдамдыгы 75 км/саат жүргөн. Эгерде ал ушул эле убакытта ылдамдыгы 90км/саат жүрсө канча аралыкты басып өтөт?
Алтын кесилиш
Геометрия эки кенге ээ: анын бири - Пифагордун теоремасы,
экинчиси-кесиндилерди ортоңку жана акыркы катыштарга бөлүү...
Биринчисин алтындын өлчөмү менен салыштырууга болот, а экинчиси баалуу ташка окшош.
Иоганн Кеплер
Түз кесиндини эки барабар бөлүккө, ошондой эле эки барабар эмес бөлүккө каалагандай катышта бөлүүгө болот. Акыркысын алтын бөлүү десек болот же кесиндини акыркы жана ортоңку катышта бөлүү.
Алтын кесилиш - бул кесиндини барабар эмес бөлүктөргө пропорционалдуу бөлүү, мында бүт кесинди чоң бөлүккө карайт, ал эми чоң бөлүктүн өзү кичинекейге карайт; же башкача айтканда, кичинекей кесинди ушундай эле чоңго карайт, чоң бардыгына карагандай: a : b = b : c же с : b = b : а.
Алтын кесилиш менен практика жүзүндө таанышууну кесиндини түз алтын пропорцияда циркулдун жана сызгычтын жардамы менен бөлүүдөн башташат.
Алтын пропорциянын кесиндилери чексиз иррационалдык бөлчөктөр менен туюнтулат AE = 0,618..., эгерде AB бирдик деп кабыл алсак, BE = 0,382...
Практикалык максатта көбүнчө жакындатылган мани 0,62 жана 0,38 ди пайдаланышат. Эгерде АВ кесиндисин 100 бөлүк деп кабыл алса, анда кесиндинин чоң бөлүгү 0,62 ге барабар, а кичинекей бөлүгү - 38 бөлүккө. Алтын кесилиштин касиетин бул сандын айланасында түзүшкөн романтикалык сырдуулуктун ореолу жана араң эле мистикалык таазим этүү эмес.
Пропорционалдуулук жаратылышта, искусстводо, архитектурада өсүмдүктүн, скульптуранын, имараттын туура жана көркөм предметтердин аныкталган өзүнчө өлчөмү ортосундагы катышты сактоону билдирет.
Алтын кесилиштин пропорциясына геометриялык фигура негизделет. Жактарынын ушундай катыштагы тик бурчтугу алтын тик бурчтук деген аталышка ээ болгон. Албетте, бул жерде алтын үч бурчтук да бар. Бул тең капталдуу үч бурчтук болот, мында каптал жактарынын узундугу негизинин узундугуна 1,618ге барабар болот.
Бизди курчаган пропорциялар
Скрипканын добушу, анын үнүнүн сулуулугу кайсы бир өлчөмдө инструменттин формасынын алтын кесилиш пропорциясы менен келишиминен түз көз каранды. Музыкалык чыгармалардын Бахадан Шостаковичке чейинки диапозонунун анализи музыкалык формалардын негизги метрдик катыштарын жана ошондой эле алтын кесилишти көрсөткөн. Ошентип, гармония закону музыкалык тизмекте, Менделеевдин таблицасында, планеталар ортосундагы аралыкта, микро- жана макрокосмосто, илимдин көптөгөн тармактарында табылган. Скульптура, архитектура, астрономия, биология, техника, психология, ж.б.- бардык жактарда алтын кесилиш өзүн көрсөтүүдө.
Пайдалуу шилтемелер
- “Түз жана тескери пропорциялык көз карандылыктар” темасына видео сабак. [Электрондук ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html (кайрылуу датасы: 24. 04. 2018)
- “Пропорция” темасына видеосабак: [Электрондук ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Proportsii.html (кайрылуу датасы: 24. 04. 2018)
- Пропорциялар теориясы: [Электрондук ресурс] // 2006-2018 ФГАУ ГНИИ ИТТ "Информика" URL: http://files.school-collection.edu.ru/dlrstore/c4d6841c-5a1e-ab8e-3524-e712079e89f0/00145619554921908.htm (кайрылуу датасы: 24. 04. 2018)
Глоссарий
Катыш – бул бир санды экинчисине бөлгөндөгү тийинди.
Пропорция – эки катыштын барабардыгы.
Фибона́ччи саны – сандын ирээттик элементтери 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …, анда биринчи эки сан 1 жана 1 ге же 0 жана 1 ге барабар, а ар бир кийинки сан мурунку эки сандын суммасына барабар.
Алтын кесилиш (алтын пропорция, гармониялык бөлүүнүн акыркы жана ортоңку катыштарынын бөлүнүүсү) - b жана a, a > b, эки чоңдугунун катыштары a/b = (a+b)/a болсо туура. a/b саны барабар катыш, байыркы грек скульптору жана архитектору Фидиянын атынан Ф грек жазма тамгасы менен белгиленет, Ф саны дагы алтын сан деп аталат.
Библиография
- Белянин В.С. Владел ли Платон кодом золотой пропорции? Анализ мифа.: [Электронный ресурс] // Академия Тринитаризма URL: http://www.trinitas.ru/rus/doc/0016/001b/00161296.htm (дата обращения: 24. 04. 2018)
- Золотое сечение: [Электронный ресурс] // МОО «Наука и техника», 1997...2018 URL: http://n-t.ru/tp/iz/zs (дата обращения: 25. 04. 2018)
- Золотое сечение в дизайне сайтов: [Электронный ресурс] // 2016 UX Guide URL: http://uxguide.ru/dizajn/zolotoe-sechenie-v-dizajne-sajtov/ (дата обращения: 25. 04. 2018)
- Золотое сечение: [Электронный ресурс] // Блог Рунмастера | © 2006-2018 URL: http://rustimes.com/blog/post_1177437753.html (дата обращения: 25. 04. 2018)
- А. С. Пушкин. Сапожник. Притча: [Электронный ресурс] //Электронная публикация — РВБ, 2000—2018 URL: http://rvb.ru/pushkin/01text/01versus/0423_36/1829/0521.htm (дата обращения: 25. 04. 2018)
- 15 примеров золотого сечения в архитектуре. Jelena Shiljajeva M.A. in History of Art, University of Glasgow: [Электронный ресурс] //URL: https://arhi1.ru/ob-arhitekture/nauka/zolotoe-sechenie (дата обращения: 25. 04. 2018)
- Ле Корбюзье: [Электронный ресурс] //ArchAndArch.ru 2010-2018 URL: http://www.archandarch.ru/архитекторы/ле-корбюзье/ (дата обращения: 25. 04. 2018)
- Видеоурок на тему «Прямая и обратная пропорциональные зависимости» [Электронный ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html (дата обращения: 24. 04. 2018)
- Видеоурок на тему «Пропорции»: [Электронный ресурс] // Znaika URL: http://znaika.ru/catalog/6-klass/matematika/Proportsii.html (дата обращения: 24. 04. 2018)
- Теория пропорций: [Электронный ресурс] // 2006-2018 ФГАУ ГНИИ ИТТ "Информика" URL: http://files.school-collection.edu.ru/dlrstore/c4d6841c-5a1e-ab8e-3524-e712079e89f0/00145619554921908.htm (дата обращения: 24. 04. 2018)
Кыргызстандын территориясында жайгашкан архитектуралык комплекстер, Борбордук Азия элинин архитектура тарыхында олуттуу орунду ээлейт жана өзүнө курулуш техника тармактарынын, архитектура жана өз убагындагы декоративдүү жасалгалоо жетишкендиктерин бириктирет.
Пифагор алтын бөлүү билимин египеттиктер менен вавилондуктардан алган деген божомол бар. Чындыгында эле Хеопс пирамидасы, храмдар, барельефтери, турмуштагы предметтер жана Тутанхамон көрүстөнүндөгү жасалгалар египеттик чеберлердин аларды түзүүдө алтын кесилиш катышын пайдалангандары күбө болуп турат. Француз архитектору Шарль Эдуард Ле Корбюзье Абидостогу Сети I фараонунун ибадатканасынын рельефинен жана Рамзес фараонунун сүрөттөлүшүндө фигуралардын пропорциясы алтын бөлүү чоңдугуна дал келээрин тапкан. Хесира көрүстөнүндөгү жыгач тактага түзүрүлгөн Зодчийдин рельефинде, колунда алтын бөлүү пропорциясын бекитүүчү ченөө инструменттерин кармап турат. Гректер акылдуу геометрлар болушкан. Алар балдарына арифметиканы дагы геометриялык фигуралардын жардамы менен окутушкан. Пифагордун квадраты жана ал квадраттын диагоналы динамикалык тик бурчтукту түзүү үчүн негиз болгон.
Байыркы грек Парфенон храмынын фасадында алтын пропорция бар. Аны касууда байыркы (антикалык) дүйнөнүн архитекторлору жана скульпторлору пайдаланган циркульдар табылган. Помпеядагы колдонулган циркульга дагы алтын бөлүү пропорциясы мүнөздүү. Алтын кесилиш терминин Леонардо да Винчи (1452-1519-жж) киргизген.
Үй ичиндеги энергияны туура бөлүштүрүү, экология менен коопсуз курулуш материалдарын шайкеш келтирүү гармониялык конструкциясы азыркы архитекторлор менен дизайнерлерге “Алтын кесилишти” түшүнүүгө жана анын принциптерин пайдаланууга түрткү болот. Бул сметаны көбөйтөт жана проектинин тереңдеп иштөө таасирин түзөт. Баасы 60-80% өсөт.
Таланттуу сүрөтчүлөр жана архитекторлор үчүн чыгармачылык процесс маалында туюу (интуитивно) эрежеси сакталат. Бирок алардын кээ бирлери бул абалды акылы менен ишке ашырат.
Белгилүү француз архитектору Шарль Эдуард Ле Корбюзье келечектеги үйдүн жана интерьердин параметрлерин эсептөө үчүн баштапкы бирдик катары кожоюндун боюн алган. Анын бардык иштери чындыгында индивидуалдуу жана гармониялуу.
Катыштарды эсепке албастан салынган үйлөрдө, пропорцияга дал келиши үчүн бөлмөлөрдү кайрадан пландоого болот. Бул үчүн эмеректи кайрадан коюштуруу же кошумча тосмо жасоо эле жетиштүү. Терезе, эшиктердин узундугу менен туурасы аналогиялык мүнөздө өзгөрөт.
Түс менен жасалгалоо кылууда жөнөкөйлөтүлгөн катышты алуу 60% негизги түс, 30%- ыраң, а калган 10% - тондорду өздөштүрүүнү күчөтүүчү эсепке жетет.
Эмеректин узундугу жана бийиктиги шыптын бийиктиги жана дубалдардын туурасы менен эсептелиши керек.
Интерьердеги бул нормалардын тиркемеси, архитектуралык оформленген тегиздик катары, өз алдынча уюштуруу, рекурсия, асимметрия, кооздук түшүнүктөрүн бириктирет.
Пропорциянын эң башкы эрежеси
Баардыгы билип эстеп калуу керек
Ортоңку мүчөлөрүн четкилерине көбөйтсөк
Бул мүчөлөрү дайыма тең болот.