Математика: Инструменты для вычислений и измерений — различия между версиями
Msu05 (обсуждение | вклад) (→Библиография) |
Admine2 (обсуждение | вклад) |
||
| (не показано 9 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
<div class="row mat-bg"> | <div class="row mat-bg"> | ||
{{Якорь|Начало}} | {{Якорь|Начало}} | ||
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> | <div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> | ||
| − | |||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | ==История измерений== |
| + | <div class="show-for-large-up">{{center|[[Файл:Istoriya_scheta_izmeren.jpg|500px]]}}</div> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:Istoriya_scheta_izmeren.jpg|500px]]}}</div> | ||
В древности человеку приходилось постепенно учиться не только считать количество предметов, но и уметь их измерять. Когда древние люди пытались найти для себя пещеру, они вынуждены были определять длину, ширину и высоту своего будущего дома с собственным ростом. А это и есть измерение. Изготовляя простейшие орудия труда, строя жилье, добывая пищу, возникает необходимость измерять расстояния, а затем площади, емкости, массу, время. Наши предки располагали только собственным ростом, длиной рук и ног. Если при счете человек пользовался пальцами рук и ног, то при измерении расстояний использовались руки и ноги. | В древности человеку приходилось постепенно учиться не только считать количество предметов, но и уметь их измерять. Когда древние люди пытались найти для себя пещеру, они вынуждены были определять длину, ширину и высоту своего будущего дома с собственным ростом. А это и есть измерение. Изготовляя простейшие орудия труда, строя жилье, добывая пищу, возникает необходимость измерять расстояния, а затем площади, емкости, массу, время. Наши предки располагали только собственным ростом, длиной рук и ног. Если при счете человек пользовался пальцами рук и ног, то при измерении расстояний использовались руки и ноги. | ||
| Строка 12: | Строка 12: | ||
Затем стали использовать различные камушки, узелки на веревках, насечки на палках и т.д. Древние торговцы использовали зерна или камешки, которые выкладывали на специальные доски. Позже стали использовать доски с камешками, на которых были углубления, по которым эти камешки передвигались. Подобное приспособление получило название абак и стало прародителем русских счетов. Сегодня для облегчения процесса счета разработано большое количество разных приборов, среди которых одним из самых распространенных является микрокалькулятор. Кроме вычислительных приборов используются измерительные приборы, которые также были изобретены в древние времена. Среди них самыми простыми и доступными является линейка и транспортир. | Затем стали использовать различные камушки, узелки на веревках, насечки на палках и т.д. Древние торговцы использовали зерна или камешки, которые выкладывали на специальные доски. Позже стали использовать доски с камешками, на которых были углубления, по которым эти камешки передвигались. Подобное приспособление получило название абак и стало прародителем русских счетов. Сегодня для облегчения процесса счета разработано большое количество разных приборов, среди которых одним из самых распространенных является микрокалькулятор. Кроме вычислительных приборов используются измерительные приборы, которые также были изобретены в древние времена. Среди них самыми простыми и доступными является линейка и транспортир. | ||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:Instrumenty_dlya_vychisl.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Instrumenty_dlya_vychisl.gif]]}}</div> |
<br clear=all /> | <br clear=all /> | ||
| Строка 36: | Строка 36: | ||
---- | ---- | ||
</div> | </div> | ||
| − | <div class="mw-collapsible mw-collapsed" id="mw-customcollapsible-TR">Для измерения углов использовались специальные инструменты, первые из которых появились более 4 тысяч лет назад в Древнем Вавилоне, где была разработана система мер для определения величины угла. Вавилоняне делили круг на 360 равных частей. Одну такую часть принято было считать единицей измерения углов. Такие единицы измерения сегодня называются градусами. Транспортир является самым простым и распространенным инструментом для измерения величины углов. Этот инструмент был изобретен еще в глубокой древности, но его современное название происходит от французского «transporter» – «переносить». Рассмотрим особенности использования транспортира. Шкала на транспортир нанесена на полуокружность, центр которой отмечен на нем черточкой. Штрихи шкалы транспортира делят полуокружность на 180 одинаковых делений. Если провести лучи из центра полуокружности через эти штрихи, то они образуют 180 углов, каждый из которых равен [[Файл:1 180 .png]] доле развернутого угла. Такие углы и называются градусами. Градусы обозначают знаком [[Файл: | + | <div class="mw-collapsible mw-collapsed" id="mw-customcollapsible-TR">Для измерения углов использовались специальные инструменты, первые из которых появились более 4 тысяч лет назад в Древнем Вавилоне, где была разработана система мер для определения величины угла. Вавилоняне делили круг на 360 равных частей. Одну такую часть принято было считать единицей измерения углов. Такие единицы измерения сегодня называются градусами. Транспортир является самым простым и распространенным инструментом для измерения величины углов. Этот инструмент был изобретен еще в глубокой древности, но его современное название происходит от французского «transporter» – «переносить». Рассмотрим особенности использования транспортира. Шкала на транспортир нанесена на полуокружность, центр которой отмечен на нем черточкой. Штрихи шкалы транспортира делят полуокружность на 180 одинаковых делений. Если провести лучи из центра полуокружности через эти штрихи, то они образуют 180 углов, каждый из которых равен [[Файл:1 180 .png]] доле развернутого угла. Такие углы и называются градусами. Градусы обозначают знаком [[Файл:Obozna_gradus.png]]. Каждое деление шкалы транспортира равно [[Файл:1_gradus.png]]. Кроме делений по [[Файл:1_gradus.png]], на транспортире есть еще деления по [[Файл:5_gradus.png]] и по [[Файл:10_gradus.png]]. Транспортир также применяют и для построения углов. |
---- | ---- | ||
</div> | </div> | ||
| Строка 51: | Строка 51: | ||
==Соотношение между единицами длины== | ==Соотношение между единицами длины== | ||
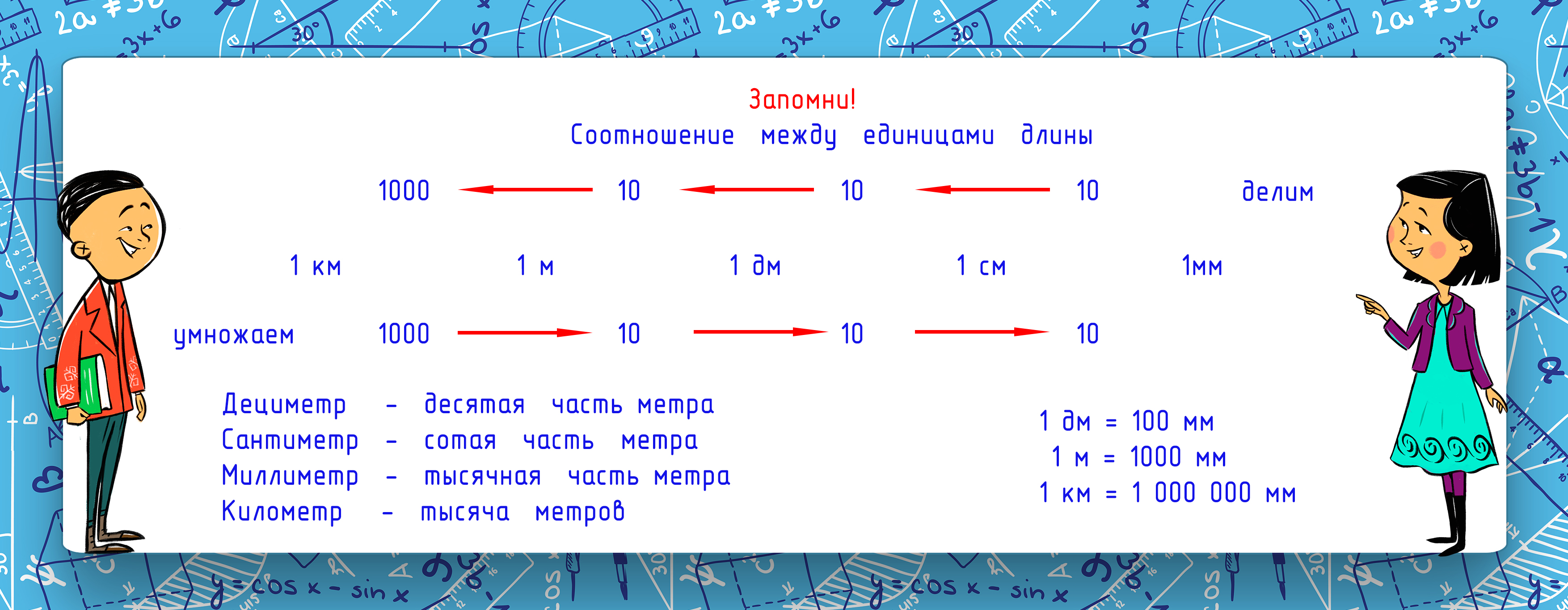
С единицами измерений длины вы знакомы. А для того, чтобы быстрее заучить основные соотношения, лучше всего выстроить единицы измерений по порядку от мм до км и составить схему. Между каждыми соседними единицами измерения стоит переводящее число, на которое в случае перевода в меньшую единицу измерения надо поделить, а в случае перевода в более крупную умножить. Если для перевода даны не соседние единицы, а расположенные через одну — надо выполнить два перехода. Через три — три перехода. В этом случае переводящее число будет составлено путем совмещения единицы и всех нулей, которые мы встречаем по дороге. При движении вправо (то есть при переводе в более мелкую единицу) мы умножаем, а при движении влево (то есть при переводе в крупную) — делим. | С единицами измерений длины вы знакомы. А для того, чтобы быстрее заучить основные соотношения, лучше всего выстроить единицы измерений по порядку от мм до км и составить схему. Между каждыми соседними единицами измерения стоит переводящее число, на которое в случае перевода в меньшую единицу измерения надо поделить, а в случае перевода в более крупную умножить. Если для перевода даны не соседние единицы, а расположенные через одну — надо выполнить два перехода. Через три — три перехода. В этом случае переводящее число будет составлено путем совмещения единицы и всех нулей, которые мы встречаем по дороге. При движении вправо (то есть при переводе в более мелкую единицу) мы умножаем, а при движении влево (то есть при переводе в крупную) — делим. | ||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:Sootnoshenie_dlinamy.jpg]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Sootnoshenie_dlinamy.jpg]]}}</div> |
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | ||
| Строка 66: | Строка 66: | ||
А вы заметили, каким выразительным и красочным делают человеческое общение пословицы и поговорки. В них отражается мудрость и история народа. Среди них есть такие, в которых речь идёт о старинных внесистемных единицах, знания о которых помогут лучше понимать язык математики, изучать историю и литературу. Давайте рассмотрим на примерах, что означают эти величины в устном народном творчестве и литературных произведениях. В каждом примере 2 задачи с иллюстрацией и решением. | А вы заметили, каким выразительным и красочным делают человеческое общение пословицы и поговорки. В них отражается мудрость и история народа. Среди них есть такие, в которых речь идёт о старинных внесистемных единицах, знания о которых помогут лучше понимать язык математики, изучать историю и литературу. Давайте рассмотрим на примерах, что означают эти величины в устном народном творчестве и литературных произведениях. В каждом примере 2 задачи с иллюстрацией и решением. | ||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:Пример_1__пословицы_и_поговорки_в_измерениях9.gif]]}}</div><br> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Пример_1__пословицы_и_поговорки_в_измерениях9.gif]]}}</div><br> |
| + | |||
| + | <div class="show-for-large-up">{{center|[[Файл:Пример 2 пословицы и поговорки в измерениях9.gif]]}}</div><br> | ||
| + | <div class="hide-for-large-up">{{center|[[Файл:Пример 2 пословицы и поговорки в измерениях9.gif]]}}</div><br> | ||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:Пример 3 пословицы и поговорки в измерениях9.gif]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Пример 3 пословицы и поговорки в измерениях9.gif]]}}</div> |
| − | |||
| − | |||
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | ||
| Строка 188: | Строка 189: | ||
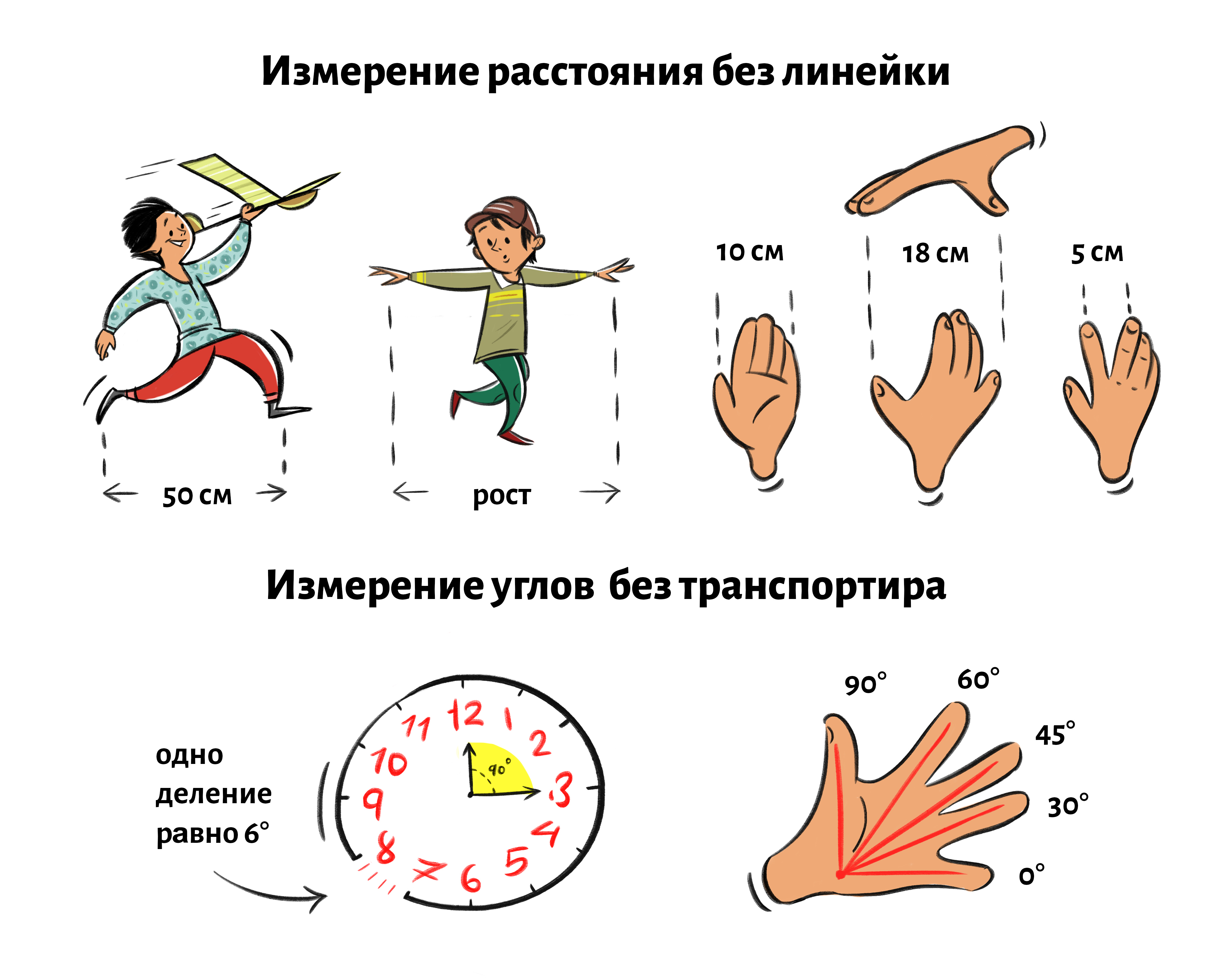
Если вам нужно приблизительно измерить предмет, но под рукой нет линейки, то для этого достаточно знать соответствие пропорций человека. Аналогично можно определить градусную меру угла без транспортира. Кстати, обычный циферблат механических часов также поможет решить эту проблему. А чтобы не забыть эту информацию, предлагаем скачать, распечатать и пользоваться. | Если вам нужно приблизительно измерить предмет, но под рукой нет линейки, то для этого достаточно знать соответствие пропорций человека. Аналогично можно определить градусную меру угла без транспортира. Кстати, обычный циферблат механических часов также поможет решить эту проблему. А чтобы не забыть эту информацию, предлагаем скачать, распечатать и пользоваться. | ||
| − | {{center|[[Файл: | + | {{center|[[Файл:Как измерить1.jpg]]}} |
| − | </div></div> | + | </div> |
| + | <div class="sbstyle"> | ||
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Пройди тестирование</div> | ||
| + | </div> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
{{lang|:KR:Математика: Эсептөө жана ченөө үчүн инструменттер}} | {{lang|:KR:Математика: Эсептөө жана ченөө үчүн инструменттер}} | ||
[[Category:Средняя школа]] | [[Category:Средняя школа]] | ||
[[Category:Математика]] | [[Category:Математика]] | ||
Текущая версия на 08:45, 22 октября 2018
Содержание
История измерений
В древности человеку приходилось постепенно учиться не только считать количество предметов, но и уметь их измерять. Когда древние люди пытались найти для себя пещеру, они вынуждены были определять длину, ширину и высоту своего будущего дома с собственным ростом. А это и есть измерение. Изготовляя простейшие орудия труда, строя жилье, добывая пищу, возникает необходимость измерять расстояния, а затем площади, емкости, массу, время. Наши предки располагали только собственным ростом, длиной рук и ног. Если при счете человек пользовался пальцами рук и ног, то при измерении расстояний использовались руки и ноги.
Затем стали использовать различные камушки, узелки на веревках, насечки на палках и т.д. Древние торговцы использовали зерна или камешки, которые выкладывали на специальные доски. Позже стали использовать доски с камешками, на которых были углубления, по которым эти камешки передвигались. Подобное приспособление получило название абак и стало прародителем русских счетов. Сегодня для облегчения процесса счета разработано большое количество разных приборов, среди которых одним из самых распространенных является микрокалькулятор. Кроме вычислительных приборов используются измерительные приборы, которые также были изобретены в древние времена. Среди них самыми простыми и доступными является линейка и транспортир.
Энциклопедия инструментов
настольная или портативная механическая вычислительная машина, предназначенная для точного умножения и деления, а также — для сложения и вычитания.
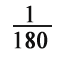доле развернутого угла. Такие углы и называются градусами. Градусы обозначают знаком 
. Каждое деление шкалы транспортира равно 
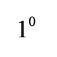. Кроме делений по 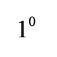, на транспортире есть еще деления по 
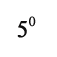и по 
. Транспортир также применяют и для построения углов.
И Средневековье свидетельствует о существовании этого удивительного инструмента, в роли которого выступали тонкие пластины из свинца. А в Древней Руси для измерения использовали металлические прутья. Конечно, мы теперь можем судить о том, что пользоваться ими было крайне неудобно, но такова история появления и развития линейки. Что такое линейка? Это прибор, воспроизводящий прямую линию на плоскости, с целью осуществления пространственных замеров. Представляет собой ровную пластину, с нанесёнными делениями, кратными единице измерения длины.
Циркуль делается из металла и состоит из двух частей, соединённых шарниром. Обычно на конце одной из них располагается игла, на конце другой — пишущий предмет.
Соотношение между единицами длины
С единицами измерений длины вы знакомы. А для того, чтобы быстрее заучить основные соотношения, лучше всего выстроить единицы измерений по порядку от мм до км и составить схему. Между каждыми соседними единицами измерения стоит переводящее число, на которое в случае перевода в меньшую единицу измерения надо поделить, а в случае перевода в более крупную умножить. Если для перевода даны не соседние единицы, а расположенные через одну — надо выполнить два перехода. Через три — три перехода. В этом случае переводящее число будет составлено путем совмещения единицы и всех нулей, которые мы встречаем по дороге. При движении вправо (то есть при переводе в более мелкую единицу) мы умножаем, а при движении влево (то есть при переводе в крупную) — делим.
Единицы измерения в повседневном общении
Значение фразеологизма «как аршин проглотил» зависит от места его употребления. Рассмотрим несколько примеров. Один из вариантов, который описывает героя, держащего осанку прямо и не двигаясь: «Что ты стоишь тут, будто аршин проглотил». Также это выражение можно употребить по отношению к человеку, который слишком долго молчит. Например: «Что приумолк? Аршин проглотил?». Следует подчеркнуть, что выражение описывает именно тот случай, когда некто держит себя слишком неестественно и чрезмерно прямо вытягивает тело. Часто данный фразеологизм употребляется в адрес людей излишне надменных. Также он может описывать чопорность человека. Теперь вы знаете в каких случаях можно использовать выражение «как аршин проглотил».
Задачи из пословиц и поговорок
А вы заметили, каким выразительным и красочным делают человеческое общение пословицы и поговорки. В них отражается мудрость и история народа. Среди них есть такие, в которых речь идёт о старинных внесистемных единицах, знания о которых помогут лучше понимать язык математики, изучать историю и литературу. Давайте рассмотрим на примерах, что означают эти величины в устном народном творчестве и литературных произведениях. В каждом примере 2 задачи с иллюстрацией и решением.
Глоссарий
У́гол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла).
Отрезок — это часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками.
Фразеологи́зм — свойственное только данному языку устойчивое сочетание слов, значение которого не определяется значением входящих в него слов, взятых по отдельности.
Полезные ссылки
Меры могут быть разные. И, кроме единиц измерения, нужен еще прибор для измерения (линейка – расстояние, секундомер время). Иногда таким прибором можем служить мы сами. Мы говорим, что от нашего дома до магазина пять минут ходьбы. Поскольку речь идёт о том, за сколько мы проходим это расстояние, то мы и выступаем в роли прибора. Более подробно об измерениях можно узнать из видеоурока «Измерение» : [Электронный ресурс] // InternetUrok.ru YouTube, 2017. URL: https://www.youtube.com/watch?v=K1KfA65cgT8 . (дата обращения: 20.11.2017)
Библиография
- Системы измерения и счет у кыргызов.: [Электронный ресурс] //Open.kg Открытый Кыргызстан. URL: https://www.open.kg/about-kyrgyzstan/culture/ethnography/1970-sistemy-izmereniya-i-schet-u-kyrgyzov.html . (дата обращения: 20.11.2017)
- Инструменты для вычислений и измерений.: [Электронный ресурс] // Avtor24, 2017. URL: https://author24.ru/spravochniki/matematika/drobnye_chisla/instrumenty_dlya_vychisleniy_i_izmereniy/ (дата обращения: 20.11.2017)
- Этим хитростям нас научили еще в школе. Полезные советы. : [Электронный ресурс] // Мы создаем общение Информационно-развлекательный портал. URL: http://uposter.ru/blog/sovet/9802.html (дата обращения: 20.11.2017)
- Видеоурок «Измерение».: [Электронный ресурс] // InternetUrok.ru YouTube, 2017. URL: https://www.youtube.com/watch?v=K1KfA65cgT8 . (дата обращения: 20.11.2017)
е было народа, который не изобрел бы собственные единицы измерения. В нашей стране существовали свои меры, начиная с самых мелких линейных единиц измерения. Длину и ширину предметов измеряли такими мерами:
чыпалактай — с мизинец,
бармактай — с большой палец,
кийиздин калындыгындай — с толщину войлока,
таман эли — с ширину ступни.
В качестве мер использовали и другие части тела человека: толщину ладони, окружность локтя, окружность бедра, окружность талии, окружность быка в поясе.
Меры ширины и толщины во многом были аналогичны мелким мерам длины, к которым только добавлялось слово узундугу:
узундугу жарым эли — длина в пол пальца,
узундугу бир эли — длина в один палец ,
карыш— расстояние между концами раздвинутых большого и среднего пальцев,
кере карыш — раздвинутую четверть,
мерген карыш или соом — расстояние между концами раздвинутых большого и указательного пальцев,
укум карыш — расстояние между концом большого пальца и согнутым указательным.
Этой мерой измерялись шесты, деревянные части юрты, ткани. Величину казанов (котлов) измеряли также карышем. Самый большой казан имел 12 карышей. В эпосах «Манас», «Курманбек», «Кедейкан» встречаются упоминания о таких казанах, а в эпосе «Эр Төштүк» рассказывается о волшебном казане кырк кулак (сорок ушек):
Кырк кулак казан бар
Кырк кулагы кырк жакка экен:
Тилек тилеп ачылган.
Есть волшебный казан «сорок ушек»:
Все «сорок ушек» до единого
Открываются, желая зла.
Употребляли и другие меры длины:
чыканак — от локтя до концов вытянутых пальцев,
кары — от локтя до плеча (это расстояние составляет примерно 40—50 см).
Ширину ткани обычно определяли мерой теш жарым — от конца вытянутой руки до середины груди. Употребляли и такую меру, как кулач — длина размаха рук, вытянутых в стороны (маховая сажень), распространенную и у других народов. Кыргызы кулачем измеряли длину арканов, ууков—жердей купола юрты, желе — привязи для жеребят, натянутой между двумя колышками, когонов — овцевязи, состоящей из длинной веревки, глубину зындана — темницы, высоту крепостей. Расстояние между концами до отказа вытянутых в сторону рук называли кере - кулач.
Для обозначения длины употребляли расстояние от двери юрты до тара — почетной стороны юрты, которое равнялось 4 или 5 метрам. Иногда пользовались и такими мерами длины: бир кадам — длина в один шаг, эки аттам — длина в два прыжка и др. С древних времен народной мерой длины является определение охотниками расстояния до цели — по дальности полета пули: бир бута атым — около 100 метров, эки бута атым — 200 метров и т. д. Расстояние, на протяжении которого слышен крик человека, равное примерно версте (1,06 км), называли чакырым. Зная эти меры длины, можно было найти другие. Обычно эсепчи, или койчу — чабаны, которым нужны были смышленые помощники, проверяли способности ребенка на решении (в уме) примерно таких задач: Аралыгы 5 чакырым жерге катары менен тыгыз тиркешкен канча ийнени коюуга болот? — Сколько иголок можно уложить рядом вплотную на расстоянии 5 чакырым? Вычисляли так: сначала узнавали, сколько иголок можно уложить по длине ширенке — спичечной коробки, затем сколько таких коробок составит 1 шаг человека, а сколько шагов составляют чакырым, было известно.
Дальние расстояния определяли следующими мерами: тай чабым — расстояние, которое проскачет жеребец в возрасте одного года без остановки — приблизительно 3 километра, купан чабым — расстояние, проделанное без отдыха двухлетним жеребцом —5—7 километров, ат чабым— расстояние скачки, в среднем составляющее 25—30 километров. Часто расстояние определяли «на глазок», при этом использовали дальние ориентиры — гору, скалу, реку, большой холм или близкие ориентиры — юрту, дерево, пасущийся скот.
Меры высоты почти не были развиты, очевидно, из-за отсутствия каких-либо высоких строений. В обиходе использовались следующие меры высоты:
тушардан — до стреножения коня,
тизе бою — высота до колена (например, тизе бою кар — снег до колена), киши бою — высота в рост человека,
кереге бою — высота деревянной решетки, образующей стены юрты,
үй бою бийик — высота с юрту,
тоо бою — высота в рост верблюда,
киши бою терен — глубина в рост человека,
тоо бою ан — яма в рост верблюда,
укурук бою терен — глубина с жердь,
укурук бою бийик — высота в длину жерди,
аркан бою бийик — высота, соизмеримая с длиной аркана.
О высоте гор говорили так: асман, или көк тиреген тоо — гора высотой до неба.
Существовало старинное измерение высоты дувала в бакса. В эпосе «Манас» рассказывается о том, что у вражеского главнокомандующего Конурбая был очень тренированный конь Алгары, который, убегая от настигавшего его Манаса, свободно перепрыгнул дувал — забор высотой в 60 баксов:
Проклятый этот конь Алгара!
Способности у него великие —
Шестидесятирядную стену
Если вам нужно приблизительно измерить предмет, но под рукой нет линейки, то для этого достаточно знать соответствие пропорций человека. Аналогично можно определить градусную меру угла без транспортира. Кстати, обычный циферблат механических часов также поможет решить эту проблему. А чтобы не забыть эту информацию, предлагаем скачать, распечатать и пользоваться.
