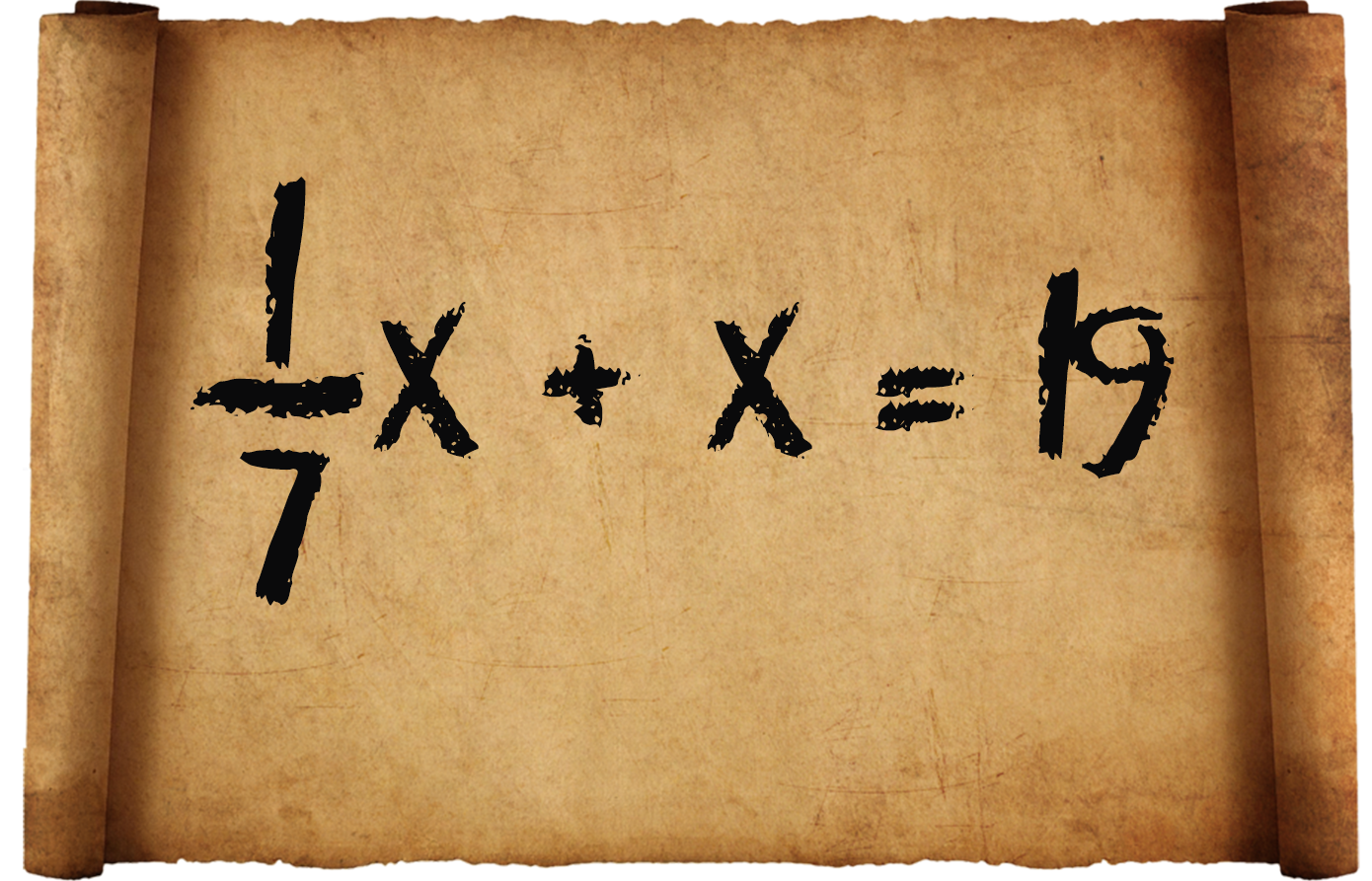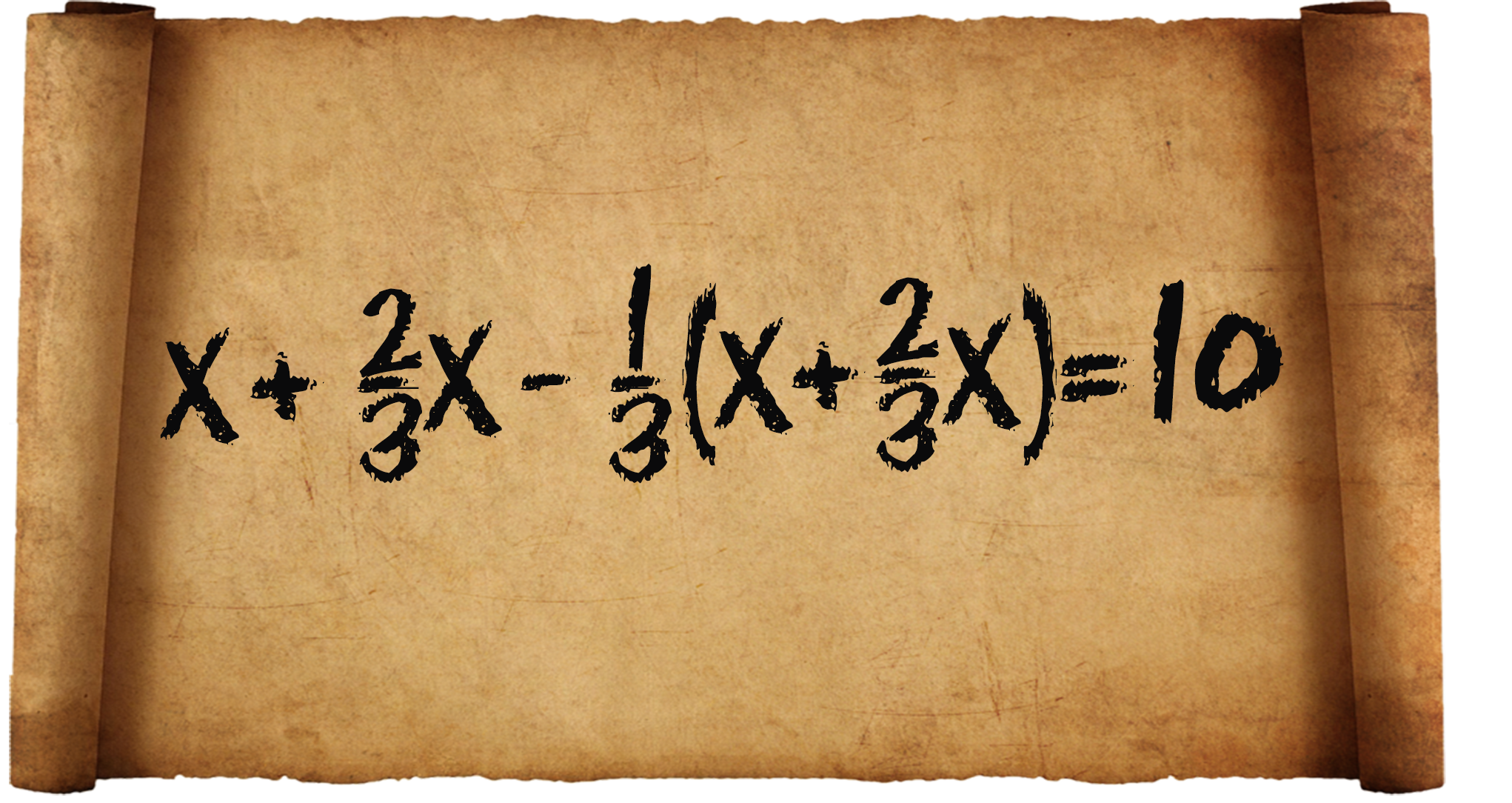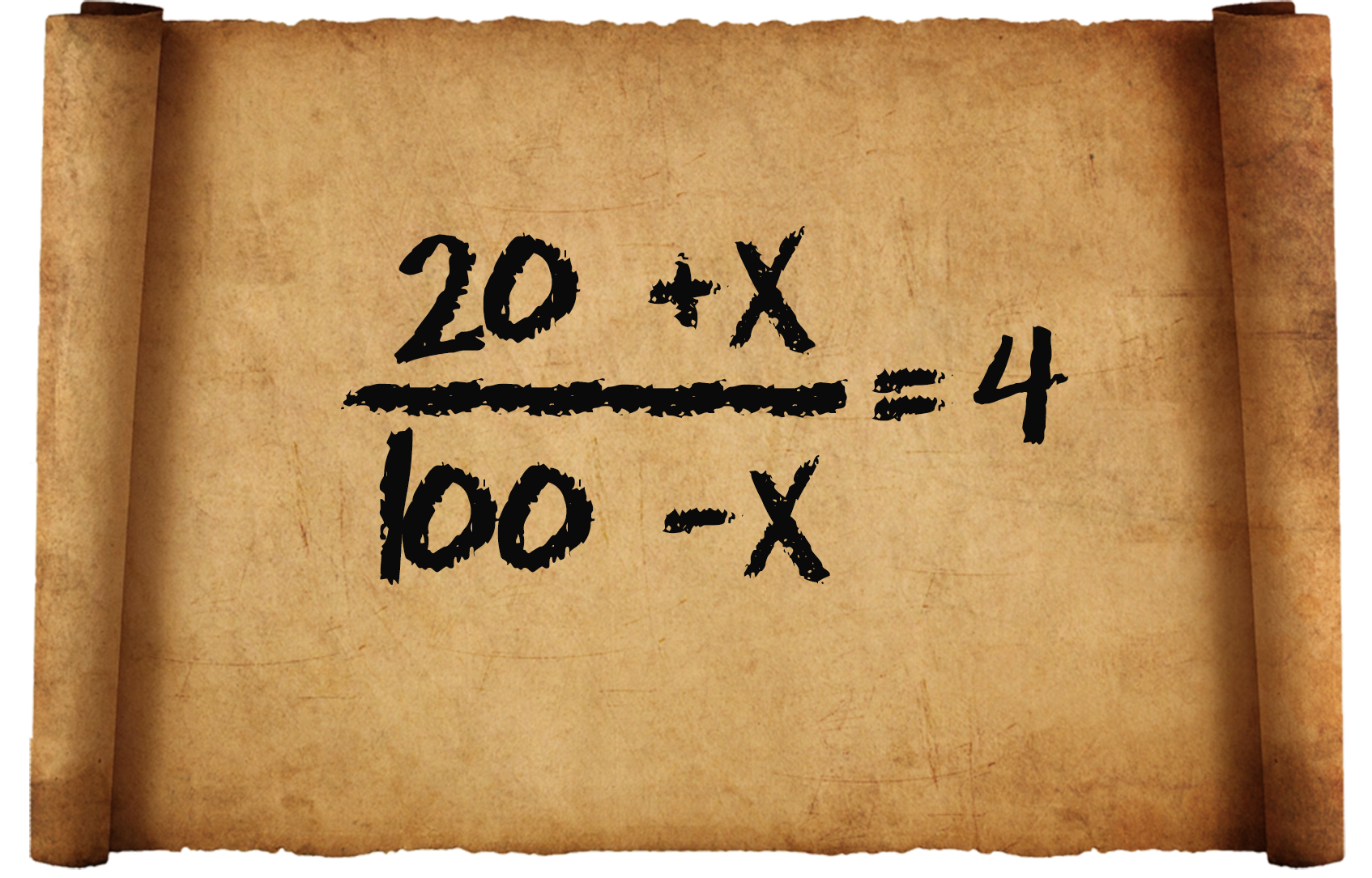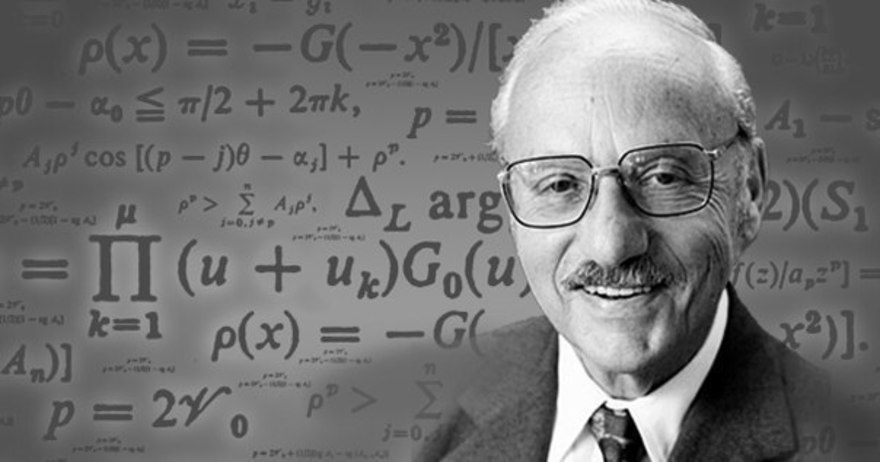БИЛИМ БУЛАГЫ

Математика: Решение уравнений — различия между версиями

(→‎Развитие математической науки в Кыргызстане)
 
(не показано 27 промежуточных версий 2 участников)
Строка 2: Строка 2:
 
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content -->  
 
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content -->  
 
{{Якорь|Начало}}
 
{{Якорь|Начало}}
−
<div class="cutok">[[#Из истории уравнений|Из истории уравнений]] [[#Развитие математической науки в Кыргызстане|Развитие математической науки в Кыргызстане]] [[#Уравнение. Корни уравнения|Уравнение. Корни уравнения]] [[#Зачем нужны уравнения|Зачем нужны уравнения]]</div>
 
  
 
==Из истории уравнений==
 
==Из истории уравнений==
Строка 17: Строка 16:
 
<ul class="large-block-grid-3 small-block-grid-1">
 
<ul class="large-block-grid-3 small-block-grid-1">
 
     <li>
 
     <li>
−
     [[file:Примеры_старинных_задач_№1.png|400px]]
+
     [[file:Примеры_старинных_задач_№1.png]]
 
   </li>
 
   </li>
 
<li>
 
<li>
−
     [[file:Примеры_старинных_задач_№2.png|400px]]
+
     [[file:Примеры_старинных_задач_№2.png]]
 
   </li>
 
   </li>
 
<li>
 
<li>
−
     [[file:Примеры_старинных_задач_№3.png|400px]]
+
     [[file:Примеры_старинных_задач_№3.png]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 41: Строка 40:
 
Сколько дал первый?»
 
Сколько дал первый?»
  
−
Получаем уравнение:  X+2X+6X+24X=132
+
Получаем уравнение:  x+2x+6x+24x=132
  
 
В рукописи задача решается способом «ложного положения». (Этим способом пользовался и Л.Ф. Магницкий в своей «Арифметике».)
 
В рукописи задача решается способом «ложного положения». (Этим способом пользовался и Л.Ф. Магницкий в своей «Арифметике».)
Строка 51: Строка 50:
 
Но общее правило для решения уравнений первой степени с одним неизвестным дал в IX веке Мухаммед аль-Хорезми.
 
Но общее правило для решения уравнений первой степени с одним неизвестным дал в IX веке Мухаммед аль-Хорезми.
  
−
<div class="show-for-large-up">{{right|[[Файл:Памятник_Ал_Хорезми_в_Ташкенте.jpg|400px]]}}</div>
+
<div class="show-for-large-up">{{right-p|[[Файл:Al_horezmi_Tashkent.jpg|400px|Памятник Аль-Хорезми в Ташкенте]]|Памятник Аль-Хорезми в Ташкенте}}</div>
−
<div class="hide-for-large-up">{{right|[[Файл:Памятник_Ал_Хорезми_в_Ташкенте.jpg|400px]]}}</div>
+
<div class="hide-for-large-up">{{right-p|[[Файл:Al_horezmi_Tashkent.jpg|400px|Памятник Аль-Хорезми в Ташкенте]]|Памятник Аль-Хорезми в Ташкенте}}</div>
  
 
В своем сочинении «'''Аль-джебр и аль-мукабала'''» он дает два приема, применяемых при решении уравнений.
 
В своем сочинении «'''Аль-джебр и аль-мукабала'''» он дает два приема, применяемых при решении уравнений.
Строка 64: Строка 63:
 
Получим:  5х+5=2х+17
 
Получим:  5х+5=2х+17
 
Применим «'''аль-мукабала'''»: вычитаем из каждой части 2x и 5. Получим:  3х=12
 
Применим «'''аль-мукабала'''»: вычитаем из каждой части 2x и 5. Получим:  3х=12
−
Отсюда легко находится х. X=4
+
Отсюда легко находится х. x=4
  
−
<div class="show-for-large-up">{{center|[[Файл:Важнейшие_факты_из_истории_уравнений.mp4|500px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Iz_istorii_uravnen.mp4|500px]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Важнейшие_факты_из_истории_уравнений.mp4|500px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Iz_istorii_uravnen.mp4|500px]]}}</div>
  
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
Строка 91: Строка 90:
 
Особое внимание уделяется исследованию по теории и приложениям интегро-дифференциальных, интегральных и дифференциальных уравнений, операционному исчислению, по разностным и суммарно-разностным уравнениям, математической физике, линейной алгебре. Больших успехов математика Кыргызстана достигла в области интегро-дифференциальных уравнений. Ученые математики надеются, что в математическую науку придут образованные, высокоинтеллектуальные, целеустремленные молодые люди и поднимут престиж математической науки Кыргызстана еще выше.
 
Особое внимание уделяется исследованию по теории и приложениям интегро-дифференциальных, интегральных и дифференциальных уравнений, операционному исчислению, по разностным и суммарно-разностным уравнениям, математической физике, линейной алгебре. Больших успехов математика Кыргызстана достигла в области интегро-дифференциальных уравнений. Ученые математики надеются, что в математическую науку придут образованные, высокоинтеллектуальные, целеустремленные молодые люди и поднимут престиж математической науки Кыргызстана еще выше.
  
−
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
+
<center>
 +
<ul class=" example-orbit" data-orbit="" data-options="animation: pause_on_hover:true; animation_speed:100; navigation_arrows:true; resume_on_mouseout: true; timer_speed:2500;" >
 
   <li class="active">
 
   <li class="active">
−
    [[file:Сухомлинов Георгий Акимович1 .jpg]]
+
{{center-p|[[file:Сухомлинов Георгий Акимович1 .jpg|Сухомлинов Георгий Акимович]]|Сухомлинов Георгий Акимович}}
−
  </li>
+
</li>
 
  <li>
 
  <li>
−
    [[file:Быков_Яков_Васильевич1.jpg]]
+
{{center-p|[[file:Быков_Яков_Васильевич1.jpg|Быков Яков Васильевич]]|Быков Яков Васильевич}}
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
  [[file:Иманалиев Муратбек Сансызбаевич1.jpg]]
+
{{center-p|[[file:Иманалиев Муратбек Сансызбаевич1.jpg|Иманалиев Муратбек Сансызбаевич]]|Иманалиев Муратбек Сансызбаевич}}
 
   </li>
 
   </li>
 
<li>
 
<li>
−
  [[file:Алтай Асылканович Борубаев.jpg]]
+
{{center-p|  [[file:Алтай Асылканович Борубаев.jpg|Алтай Асылканович Борубаев]]|Алтай Асылканович Борубаев}}
 
   </li>
 
   </li>
 
<li>
 
<li>
−
    [[file:Жусупбаев Амангельди1.jpg]]
+
{{center-p|    [[file:Жусупбаев Амангельди1.jpg|Жусупбаев Амангельди]]|Жусупбаев Амангельди}}
 
   </li>
 
   </li>
 
<li>
 
<li>
−
    [[file:Байзаков_Асан1.jpg]]
+
{{center-p|    [[file:Байзаков_Асан1.jpg|Байзаков_Асан]]|Байзаков_Асан}}
 
   </li>
 
   </li>
 
<li>
 
<li>
−
    [[file:Панков Павел Сергеевич1.jpg]]
+
  {{center-p|    [[file:Панков Павел Сергеевич1.jpg|Панков Павел Сергеевич]]|Панков Павел Сергеевич}}
 
   </li>
 
   </li>
 
</ul>
 
</ul>
  
 +
</center>
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
Строка 127: Строка 128:
 
Пример 2.  Уравнение (5 + x)(x - 6)=0 имеет два корня: -5 и 6.
 
Пример 2.  Уравнение (5 + x)(x - 6)=0 имеет два корня: -5 и 6.
  
−
Пример 3. 9 + x2 = 0 не имеет корней на множестве вещественных чисел.
+
Пример 3. 9 + x<sup>2</sup> = 0 не имеет корней на множестве вещественных чисел.
  
 
'''Линейные уравнения'''
 
'''Линейные уравнения'''
Строка 135: Строка 136:
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
   <li class="active">
 
   <li class="active">
−
     [[file:Для_линейного_уравнения_возможны_случаи.gif|300px]]
+
     [[file:Для_линейного_уравнения_возможны_случаи.gif]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Формулы_для_решения_уравнений.gif|300px]]
+
     [[file:Формулы_для_решения_уравнений.gif]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 165: Строка 166:
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
   <li class="active">
 
   <li class="active">
−
     [[file:Пример_Решение_уравнений.gif|300px]]
+
     [[file:Пример_Решение_уравнений.gif]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file:Пример_Решение_уравнений_2.gif|300px]]
+
     [[file:Пример_Решение_уравнений_2.gif]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
   [[file:Пример_Решение_уравнений_3.gif|300px]]
+
   [[file:Пример_Решение_уравнений_3.gif]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 193: Строка 194:
 
<ul class="large-block-grid-3 small-block-grid-1">
 
<ul class="large-block-grid-3 small-block-grid-1">
 
     <li>
 
     <li>
−
     [[file:Пример_Решение_задач_1.gif|400px]]
+
     [[file:Пример_Решение_задач_1.gif]]
 
   </li>
 
   </li>
 
<li>
 
<li>
−
     [[file:Пример_Решение_задач_2.gif|400px]]
+
     [[file:Пример_Решение_задач_2.gif]]
 
   </li>
 
   </li>
 
<li>
 
<li>
−
     [[file:Пример_Решение_задач_3.gif|400px]]
+
     [[file:Пример_Решение_задач_3.gif]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 240: Строка 241:
 
<div class="large-4 medium-5 columns">
 
<div class="large-4 medium-5 columns">
 
<!-- четвертый элемент сайдбара лайфхак -->
 
<!-- четвертый элемент сайдбара лайфхак -->
−
<div class="shadow radius sbstyle" style="margin-top:20px;">
+
<div class="sbstyle" style="margin-top:20px;">
 
<div class="row">
 
<div class="row">
 
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Основные математические знаки</div>
 
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Основные математические знаки</div>
Строка 246: Строка 247:
 
Знаки плюса и минуса придумали в немецкой математической школе  алгебраистов. Они используются в «Арифметике» Иоганна Видмана (Johannes Widmann), изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов не ясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа практически мгновенно получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
 
Знаки плюса и минуса придумали в немецкой математической школе  алгебраистов. Они используются в «Арифметике» Иоганна Видмана (Johannes Widmann), изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов не ясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа практически мгновенно получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
  
−
{{center|[[Файл:Первое_появление_знаков_«плюс»_и_«минус»._Страница_из_книги_Иоганна_Видмана..gif]]}}
+
{{center|[[Файл:Plus_minus_Vidman.gif]]}}
  
 
Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. В конце XVII века  Лейбниц заменил крестик на точку, чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).
 
Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. В конце XVII века  Лейбниц заменил крестик на точку, чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).
Строка 311: Строка 312:
  
 
<!-- четвертый элемент сайдбара лайфхак -->
 
<!-- четвертый элемент сайдбара лайфхак -->
−
<div class="shadow radius sbstyle" style="margin-top:20px;">
+
<div class="sbstyle" style="margin-top:20px;">
 
<div class="row">
 
<div class="row">
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">[[Файл:Головоломки.jpg|50px]]</div>
+
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Математический софизм</div>
 
</div>
 
</div>
 +
<div class="mw-customtoggle-ppol button17">''' ''Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
 +
                Мартин Гарднер''</div>
 +
 +
<div class="mw-collapsible mw-collapsed" id="mw-customcollapsible-ppol">
 +
Разбор и решение разнообразных задач помогает развивать смекалку и логику. Математические софизмы относятся именно к таким задачам. Однако следует помнить, что в математике важна аккуратность. Каждый шаг от одной логической конструкции к другой должен быть точным, тщательно выверенным. Один неверный переход может привести не просто к неточности, а к большой ошибке.
 +
 +
Выделяют три вида математических софизмов:
 +
 +
1. Арифметические
 +
2. Алгебраические
 +
3. Геометрические
 +
 +
1) «Один сом не равен ста тыйынам»
 +
 +
{{center|[[Файл:1_сом_=_100_тыйын.gif]]}}
 +
 +
Если обе части верного числового равенства умножить на любое число или разделить на отличное от нуля число, то получится верное числовое равенство, т.е  если a=b, c=d, то ac=bd.
 +
 +
Запишем два очевидным равенства:
 +
 +
1 сом =100 тыйынам (1)
 +
 +
10  сом = 10 ∙ 100  тыйын (2)
 +
 +
Перемножив соответствующие части равенств, получим:
 +
 +
10 сом =100 000  тыйын (3)
 +
 +
и, наконец, разделив последнее равенство на 10 получим, что
 +
 +
1 сом  = 10 000 тыйын
 +
 +
Таким образом, один сом не равен ста тыйынам. Где ошибка?
 +
 +
Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.
 +
 +
Действительно, перемножая равенства (1) и (2), мы получим не (3), а следующее равенство 10 сом =100 000 тыйын, которое после деления на 10 дает 1 сом = 10 000 тыйын, а не равенство 1 сом = 10 000 тыйын, как это записано в условии софизма.
 +
 +
2) 4 = 5.
 +
 +
{{center|[[Файл:4=5.gif]]}}
 +
 +
Доказательство. Возьмем два числа а&nbsp;=&nbsp;4 и b&nbsp;=&nbsp;5, их полусумму обозначим через с&nbsp;=&nbsp;(а+b)/2.
 +
 +
Тогда а = 2с - b и 2с - а = b.
 +
 +
Перемножив эти равенства почленно, получим:
 +
 +
а<sup>2</sup> - 2ас = b<sup>2</sup> - 2 bс.
 +
 +
Прибавив к обеим частям  с<sup>2</sup>, получим:
 +
 +
а<sup>2</sup> - 2ас + с<sup>2</sup> = b<sup>2</sup> -  2bс + с<sup>2</sup>,
 +
 +
или (а - с)<sup>2</sup> = (b - с)<sup>2</sup>.
 +
 +
Значит, а – с = b - с, откуда а = 6, то есть 4&nbsp;=&nbsp;5.
 +
 +
Ошибка, допущенная в этом софизме: если квадраты чисел равны, то сами числа не обязательно равны, они могут быть и противоположными. Равенство а&nbsp;-&nbsp;с&nbsp;=&nbsp;b&nbsp;-&nbsp;с в данном случае неверно, должно быть а&nbsp;-&nbsp;с&nbsp;=&nbsp;b&nbsp;-&nbsp;с или а&nbsp;-&nbsp;с&nbsp;=&nbsp;с&nbsp;-&nbsp;b.
 +
 +
3) «Спичка вдвое длиннее телеграфного столба».
 +
 +
{{center|[[Файл:Спичка_и_телеграфный_столб.gif]]}}
 +
 +
Доказательство.
 +
 +
Пусть а длина спички и b - длина столба. Разность между b и a обозначим через c.
 +
 +
Имеем, b - a = c, b = a + c.
 +
 +
Перемножим два этих равенства по частям, находим: b<sup>2</sup> - ab = ca + c<sup>2</sup>.
 +
 +
Вычтем из обеих частей bc. Получим: b<sup>2</sup>- ab - bc = ca + c<sup>2</sup> - bc, или
 +
 +
b(b - a - c) = - c(b - a - c), откуда
 +
 +
b = - c, но c = b - a, поэтому b = a - b, или a = 2b.
 +
 +
Ошибка заключается в том, что в равенстве выражений b(b-a-c )=-c(b-a-c) производится деление на 0 (b - a - c =  с - с = 0).
 +
 +
</div>
 +
{{center|[[Файл:Головоломки.jpg]]}}
  
 
Школьник зашел в лавочку возле школы. На прилавке лежали ручки по 30 рублей за штуку и карандаши по 15 рублей. Мальчик приобрел один карандаш и пошел к выходу, но по дороге подумал: «Я уже отдал продавцу 15 рублей, значит, если вернуть покупку, в сумме на моем счету окажется 30 руб». Сможет ли школьник теперь купить ручку? Почему?
 
Школьник зашел в лавочку возле школы. На прилавке лежали ручки по 30 рублей за штуку и карандаши по 15 рублей. Мальчик приобрел один карандаш и пошел к выходу, но по дороге подумал: «Я уже отдал продавцу 15 рублей, значит, если вернуть покупку, в сумме на моем счету окажется 30 руб». Сможет ли школьник теперь купить ручку? Почему?
Строка 335: Строка 418:
 
<br>
 
<br>
 
</div>
 
</div>
 +
  
 
2. Перед вами неверное неравенство 7+4-4=0.Как, переложив одну спичку, сделать его правильным?
 
2. Перед вами неверное неравенство 7+4-4=0.Как, переложив одну спичку, сделать его правильным?
Строка 361: Строка 445:
 
{{center|[[Файл:Кроссворд1.gif]]}}
 
{{center|[[Файл:Кроссворд1.gif]]}}
  
 +
</div>
 +
<div class="sbstyle">
 +
<div class="row">
 +
<div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Пройди тестирование</div>
 +
</div>
 +
 
</div>
 
</div>
 
</div>
 
</div>

Текущая версия на 08:46, 22 октября 2018

Из истории уравнений

                                            Уравнения для меня важнее, 
                                               потому что политика — для настоящего, 
                                               а уравнения — для вечности. 
                                               Альберт Эйнштейн

Еще в глубокой древности в математических сочинениях встречались уравнения, а также задачи, решаемые с помощью уравнений. Так, в египетском папирусе около 2000 лет до нашей эры (причем, как указывает в нем автор, писец Ахмес, это математическое сочинение является копией с другого, более древнего сочинения) имелись задачи на отыскание неизвестного числа. Это неизвестное называлось «хау» (куча) и обозначалось особым иероглифом.

Современная запись старинных задач

  • Примеры старинных задач №1.png
  • Примеры старинных задач №2.png
  • Примеры старинных задач №3.png

1) «Неизвестное, его седьмая часть, его целое составляет 19».

2) «2 3.png сложено и 1 3.png отнята: остаток 10». Судя по приведённому в папирусе решению, задачу следует понимать так: к неизвестному прибавлено 2 3.png его и отнята 1 3.png полученной суммы; остаток 10; найти число. Ответ: х=9

3) У Диофанта также встречаются уравнения с одним неизвестным, например: «Числа 20 и 100. Нужно одно и то же число прибавить к меньшему и вычесть из большего; отношение суммы к разности равно 4».

4) В индийской рукописной арифметике VII и VIII века нашей эры, являющейся копией с более древней рукописи (III-IV века), имеется такая задача:

«Из четырех жертвователей второй дал вдвое больше первого, третий втрое больше второго, четвертый вчетверо больше третьего, а все вместе дали 132. Сколько дал первый?»

Получаем уравнение: x+2x+6x+24x=132

В рукописи задача решается способом «ложного положения». (Этим способом пользовался и Л.Ф. Магницкий в своей «Арифметике».)

«Если бы первый дал 1, то второй бы 2, третий 6, четвертый 24, а все вместе 33. Но всего было 132, то есть вчетверо больше. Значит, и каждый из жертвователей дал вчетверо больше».

Ответ: 4; 8; 24; 96.

Но общее правило для решения уравнений первой степени с одним неизвестным дал в IX веке Мухаммед аль-Хорезми.

Памятник Аль-Хорезми в Ташкенте
Памятник Аль-Хорезми в Ташкенте

В своем сочинении «Аль-джебр и аль-мукабала» он дает два приема, применяемых при решении уравнений.

1) Прием «аль-джебр» заключается в том, что если имеются в уравнении отрицательные (вычитаемые) члены, то следует прибавить противоположные им члены к обеим частям уравнения, и тогда все члены будут положительными.

2) Прием «аль-мукабала» заключается в вычитании из обеих частей уравнения одинаковых членов, что приводит к его упрощению.

Например, дано уравнение: 5х-17=2х-5 Применим «аль-джебр»: прибавляем к каждой части уравнения 5 и 17. Получим: 5х+5=2х+17 Применим «аль-мукабала»: вычитаем из каждой части 2x и 5. Получим: 3х=12 Отсюда легко находится х. x=4

В начало

Развитие математической науки в Кыргызстане

Математика как школьный предмет начала изучаться в Кыргызстане только после Октябрьской революции, а высшая математика - после открытия первого в Кыргызстане ВУЗа - Кыргызского государственного педагогического института - ныне Кыргызского национального университета им. Ж. Баласагына.

Систематические исследования по математике в Кыргызстане начались в 1940 году, на семинаре под руководством профессора Г.А. Сухомлинова. В 1949-1965 годы семинаром руководил профессор Я.В. Быков, ставший в 1960 году членом-корреспондентом АН Киргизской ССР, с 1966 г. этот семинар, ставший уже общереспубликанским, в стенах Института возглавил М.И. Иманалиев, академик АН Киргизской ССР (1979) и член-корреспондент АН СССР (1981 год).

В 1955 году был организован Отдел физики, математики и механики при Президиуме АН Киргизской ССР, в составе которого были, тогда еще кандидаты наук, Я.В. Быков и М.И. Иманалиев. В 1960 году Отдел был преобразован в Институт физики, математики и механики. В 1962 году он стал называться Институтом физики и математики, а в 1984 году на базе математических лабораторий Института физики и математики был организован Институт математики. На его базе в 2008 году был создан Институт теоретической и прикладной математики, а с 11 мая 2017 года он переименован в Институт математики НАН КР.

С 1984 года по 2016 год Институтом руководил академик М.И. Иманалиев, с 2016 года по настоящее время руководителем Института является академик А.А. Борубаев.

Деятельность Института определяется следующими основными направлениями научных исследований:

  • Равномерные и топологические пространства и их отображения.
  • Функциональные пространства.
  • Динамические системы, описываемые разностными, дифференциальными и интегро-дифференциальными уравнениями, в том числе сингулярно-возмущенными.
  • Интегральные уравнения, некорректные и обратные задачи.
  • Оптимизационные экономические задачи.
  • Компьютеризация научных исследований, интерактивное представление объектов.

Особое внимание уделяется исследованию по теории и приложениям интегро-дифференциальных, интегральных и дифференциальных уравнений, операционному исчислению, по разностным и суммарно-разностным уравнениям, математической физике, линейной алгебре. Больших успехов математика Кыргызстана достигла в области интегро-дифференциальных уравнений. Ученые математики надеются, что в математическую науку придут образованные, высокоинтеллектуальные, целеустремленные молодые люди и поднимут престиж математической науки Кыргызстана еще выше.

  • Сухомлинов Георгий Акимович
  • Быков Яков Васильевич
  • Иманалиев Муратбек Сансызбаевич
  • Алтай Асылканович Борубаев
  • Жусупбаев Амангельди
  • Байзаков_Асан
  • Панков Павел Сергеевич
В начало

Уравнение. Корни уравнения

Равенство с переменной называют уравнением.

Каждое значение переменной, при котором данное уравнение превращается в верное равенство, называется корнем уравнения. Решить уравнение - это значит найти все его корни или доказать, что их нет. Уравнение может иметь один, два, несколько, множество корней или не иметь их вовсе.

Пример 1. Уравнение 5 + x = 15 имеет единственный корень x = 10, так как только при этом значении переменной 5 + x = 15 является верным равенством.

Пример 2. Уравнение (5 + x)(x - 6)=0 имеет два корня: -5 и 6.

Пример 3. 9 + x2 = 0 не имеет корней на множестве вещественных чисел.

Линейные уравнения

Линейным уравнением с одной переменной х называют уравнение вида ax = b, где a, b –вещественные числа; а называют коэффициентом при переменной, b - свободным членом.

  • Для линейного уравнения возможны случаи.gif
  • Формулы для решения уравнений.gif

Равносильность уравнений

Уравнения, имеющие одни и те же корни, называются равносильными уравнениями. Равносильными считаются и уравнения, у которых нет корней.

Пример 4. Уравнения x + 5 = 7 и x - 8 = -6 равносильны, так каждое из них имеет единственный корень, равный 2.

Пример 5. Уравнения 9 + x2 = 0 и 3x2 + 27 = 0 равносильны, так как каждое из них не имеет корней.

Пример 6. Уравнения 9 - x2 = 0 и x + 4 = 7 неравносильны, так как первое уравнение имеет два корня: 3 и -3, а второе только один корень: 3.

Когда уравнение решают, его стараются заменить на более простое, равносильное данному. Поэтому необходимо знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.

Теорема 1. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.

Например, уравнение x2 + 4 = 2x равносильно уравнению x2 + 4 - 2x = 0.

Теорема 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Например, уравнение (x-5)/4 =4x равносильно уравнению x-5=16x.Обе части первого уравнения умножили на 4.

Рассмотрим на примерах решение уравнений.

  • Пример Решение уравнений.gif
  • Пример Решение уравнений 2.gif
  • Пример Решение уравнений 3.gif
В начало

Зачем нужны уравнения

Вычислительные задачи бывают прямые и косвенные. Решение первых диктуется самим условием задачи, а из условия косвенной задачи не видно, какие действия приведут к ее решению. При так называемом арифметическом решении нужно проявить подчас большую изобретательность, чтобы наметить план решения косвенной задачи. Каждая новая задача требует создания нового плана. Для рационализации вычислительного процесса и был создан метод уравнений, который является основным предметом изучения в алгебре. Таким образом, уравнения нужны для того, чтобы механизировать процесс вычисления. После того как уравнение составлено, решение его можно получить вполне автоматически. Вся трудность решения задачи сводится лишь к составлению уравнения.

Составить уравнение – это значит выразить в математической форме связь между известными задачи и неизвестными ее величинами.

Рассмотрим решение задач с помощью уравнений.

Задача 1. Мама в два раза старше сына. Десять лет назад она была старше сына в три раза. Сколько лет маме?

Задача 2. В трех коробках лежит 56 карандашей. Известно, что в первой коробке их в два раза больше, чем во второй, и в 2,5 раза меньше, чем в третьей коробке. Сколько карандашей в каждой коробке?

Задача 3. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.

  • Пример Решение задач 1.gif
  • Пример Решение задач 2.gif
  • Пример Решение задач 3.gif
В начало

Полезные ссылки

Первоначальные способы решения уравнений были достаточно сложными и разнообразными. В процессе развития математики произошло их значительное упрощение, и для каждого типа уравнений появился единый алгоритм решения. Более подробно можете увидеть: [Электронный ресурс] // novykrug YouTube, 2018. URL:https://www.youtube.com/watch?v=WpwOQHVB5s4 (дата обращения: 28. 04. 2018)

Математическая модель - это способ описания реальной жизненной ситуации (задачи) с помощью математического языка. На нашем этапе изучения алгебры мы будем использовать математическое моделирование, как помощь в решении задач.:[Электронный ресурс] // school-assistant.ru © 2016 URL: http://school-assistant.ru/?predmet=algebra&theme=matemat_model (дата обращения: 28. 04. 2018)

Применение линейных уравнений очень распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Линейные уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Линейное уравнение представляет собой алгебраическое уравнение, полная степень многочленов которого равна единице. Существует множество способов решения данных уравнений. Чтобы решить уравнения данного рода необходимо найти значение переменной.:[Электронный ресурс] // © Pocket Teacher. https://pocketteacher.ru/linear-equations-2-ru (дата обращения: 28. 04. 2018)

В начало

Глоссарий

  • Алгебра – это раздел математики, который изучает общие свойства действий над различными величинами и решение уравнений, связанных с этими действиями.
  • Веще́ственное число (от лат. realis — действительный) — математический объект, возникший из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких вычислительных операций, как извлечение корня, вычисление логарифмов, решение алгебраических уравнений, исследование поведения функци
  • Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
  • Теоре́ма (др.-греч. θεώρημα — «доказательство, вид; взгляд; представление, положение») — утверждение, выводимое в рамках рассматриваемой теории из множества аксиом посредством использования конечного множества правил вывода.
  • Теорема Виета: сумма корней приведенного квадратного уравнения x2+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену: x1+x2=-p; x1∙x2=q.
В начало

Библиография


В начало

Основные математические знаки

Знаки плюса и минуса придумали в немецкой математической школе алгебраистов. Они используются в «Арифметике» Иоганна Видмана (Johannes Widmann), изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов не ясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа практически мгновенно получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.

Plus minus Vidman.gif

Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. В конце XVII века Лейбниц заменил крестик на точку, чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).

  • Уильям Отред.jpg
  • Региомонта́н (Йоганн Мюллер).jpg

Знаки деления. Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл в середине XVII века.

  • Лейбниц, Готфрид Вильгельм.jpg
  • Йоханн Ран.jpg
  • Роберт Рекорд.Мемориальная доска.jpg

Знак равенства предложил Роберт Рекорд 1510—1558) в 1557 году. Он пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. В континентальной Европе знак равенства был введён Лейбницем.

  • Леонард Эйлер.jpg
  • Томас Хэрриот.jpg
  • Джон Валлис.jpg

Знак «не равно» впервые встречается у Эйлера.Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше, меньше. Символы нестрогого сравнения предложил Джон Валлис. Первоначально черта была выше знака сравнения, а не под ним, как сейчас.

Математика – как высокая винтовая лестница,

чтобы взойти по ней к вершинам знаний,

надо пройти каждую ступеньку от первой до последней.

Джордж Бернард Данциг.jpg

Американский математик Джордж Бернард Данциг , будучи аспирантом университета, однажды опоздал на урок и принял написанные на доске уравнения за домашнее задание. Оно показалось ему сложнее обычного, но через несколько дней он смог его выполнить. Оказалось, что он решил две «нерешаемые» проблемы в статистике, над которыми бились многие учёные.

Решаем уравнения на Android за 1 секунду
Математический софизм
' Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Мартин Гарднер

Разбор и решение разнообразных задач помогает развивать смекалку и логику. Математические софизмы относятся именно к таким задачам. Однако следует помнить, что в математике важна аккуратность. Каждый шаг от одной логической конструкции к другой должен быть точным, тщательно выверенным. Один неверный переход может привести не просто к неточности, а к большой ошибке.

Выделяют три вида математических софизмов:

1. Арифметические 2. Алгебраические 3. Геометрические

1) «Один сом не равен ста тыйынам»

1 сом = 100 тыйын.gif

Если обе части верного числового равенства умножить на любое число или разделить на отличное от нуля число, то получится верное числовое равенство, т.е если a=b, c=d, то ac=bd.

Запишем два очевидным равенства:

1 сом =100 тыйынам (1)

10 сом = 10 ∙ 100 тыйын (2)

Перемножив соответствующие части равенств, получим:

10 сом =100 000 тыйын (3)

и, наконец, разделив последнее равенство на 10 получим, что

1 сом = 10 000 тыйын

Таким образом, один сом не равен ста тыйынам. Где ошибка?

Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.

Действительно, перемножая равенства (1) и (2), мы получим не (3), а следующее равенство 10 сом =100 000 тыйын, которое после деления на 10 дает 1 сом = 10 000 тыйын, а не равенство 1 сом = 10 000 тыйын, как это записано в условии софизма.

2) 4 = 5.

4=5.gif

Доказательство. Возьмем два числа а = 4 и b = 5, их полусумму обозначим через с = (а+b)/2.

Тогда а = 2с - b и 2с - а = b.

Перемножив эти равенства почленно, получим:

а2 - 2ас = b2 - 2 bс.

Прибавив к обеим частям с2, получим:

а2 - 2ас + с2 = b2 - 2bс + с2,

или (а - с)2 = (b - с)2.

Значит, а – с = b - с, откуда а = 6, то есть 4 = 5.

Ошибка, допущенная в этом софизме: если квадраты чисел равны, то сами числа не обязательно равны, они могут быть и противоположными. Равенство а - с = b - с в данном случае неверно, должно быть а - с = b - с или а - с = с - b.

3) «Спичка вдвое длиннее телеграфного столба».

Спичка и телеграфный столб.gif

Доказательство.

Пусть а длина спички и b - длина столба. Разность между b и a обозначим через c.

Имеем, b - a = c, b = a + c.

Перемножим два этих равенства по частям, находим: b2 - ab = ca + c2.

Вычтем из обеих частей bc. Получим: b2- ab - bc = ca + c2 - bc, или

b(b - a - c) = - c(b - a - c), откуда

b = - c, но c = b - a, поэтому b = a - b, или a = 2b.

Ошибка заключается в том, что в равенстве выражений b(b-a-c )=-c(b-a-c) производится деление на 0 (b - a - c = с - с = 0).

Головоломки.jpg

Школьник зашел в лавочку возле школы. На прилавке лежали ручки по 30 рублей за штуку и карандаши по 15 рублей. Мальчик приобрел один карандаш и пошел к выходу, но по дороге подумал: «Я уже отдал продавцу 15 рублей, значит, если вернуть покупку, в сумме на моем счету окажется 30 руб». Сможет ли школьник теперь купить ручку? Почему?

Ответ


Не сможет.

В качестве объяснения приведем небольшую шутку.

Студент заказал в кафе булочку, но затем решил, что не слишком голоден и обменял ее на чашечку кофе. Выпив напиток, он направился к выходу, не расплатившись. Cамо собой, за ним побежала буфетчица.

- Вы не заплатили за кофе!

- Да, все верно, но я же взял его взамен булочки!

- Так булка тоже не оплачена!

- Верно, но я ведь ее и не ел!


2. Перед вами неверное неравенство 7+4-4=0.Как, переложив одну спичку, сделать его правильным?

Головоломка со спичками.gif


3. Реши кроссворд.

По горизонтали.

4. Равенство двух отношений.

5. Французский математик, который установил связь между коэффициентами уравнения и его корнями.

По вертикали.

1. Значение переменной в уравнении.

2. Равенство, содержащее переменную.

3. Уравнение вида ax=b.

4. Неизвестное число в уравнении.

Кроссворд1.gif
Пройди тестирование
Пройди тестирование


Источник — «https://bb.edu.gov.kg/index.php?title=Математика:_Решение_уравнений&oldid=27426»