Математика: Натуральные числа — различия между версиями
Msu05 (обсуждение | вклад) (→Библиография) |
Admine2 (обсуждение | вклад) |
||
| (не показано 15 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
<div class="row mat-bg"> | <div class="row mat-bg"> | ||
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> | <div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content --> | ||
{{Якорь|Начало}} | {{Якорь|Начало}} | ||
| − | |||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:Derevo natural numbers.gif|400px]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Derevo natural numbers.gif|400px]]}}</div> |
<br> | <br> | ||
| Строка 17: | Строка 15: | ||
Натуральные числа также употребляют, чтобы выразить результаты измерения различных величин: длины, площади, времени, скорости. Кроме натуральных чисел мы знаем ещё число 0 (нуль). При счёте число нуль не используется, а означает оно «ни одного». Поэтому число 0 (нуль) не является натуральным! | Натуральные числа также употребляют, чтобы выразить результаты измерения различных величин: длины, площади, времени, скорости. Кроме натуральных чисел мы знаем ещё число 0 (нуль). При счёте число нуль не используется, а означает оно «ни одного». Поэтому число 0 (нуль) не является натуральным! | ||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:Ryad_natural_numers.mp4|400px]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Ryad_natural_numers.mp4|400px]]}}</div> |
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | ||
| Строка 28: | Строка 26: | ||
Древние кыргызы употребляли известные цивилизованному миру действительные математические числа и могли сосчитать членов своей семьи, домашних животных, стрелы в колчане лука, убитых или пойманных на охоте зверей, птиц. | Древние кыргызы употребляли известные цивилизованному миру действительные математические числа и могли сосчитать членов своей семьи, домашних животных, стрелы в колчане лука, убитых или пойманных на охоте зверей, птиц. | ||
| − | <div class="show-for-large-up">{{center|[[Файл: | + | <div class="show-for-large-up">{{center|[[Файл:Natural_numbers_kyrg.gif|600px]]}}</div> |
| − | <div class="hide-for-large-up">{{center|[[Файл: | + | <div class="hide-for-large-up">{{center|[[Файл:Natural_numbers_kyrg.gif|600px]]}}</div> |
В быту с помощью понятия «бирдин үчү» говорили о небольшом количестве предметов. Например, два — три, три — четыре, пять — шесть). Анын чакан үйүнүн төрүндө бирдин үчү болуп олтурушкан кишилер — В его маленькой юрте на почетном месте сидели несколько (немного) человек или Бирдин үчү эле малы бар — У него немного скота (три — четыре, пять — шесть голов). | В быту с помощью понятия «бирдин үчү» говорили о небольшом количестве предметов. Например, два — три, три — четыре, пять — шесть). Анын чакан үйүнүн төрүндө бирдин үчү болуп олтурушкан кишилер — В его маленькой юрте на почетном месте сидели несколько (немного) человек или Бирдин үчү эле малы бар — У него немного скота (три — четыре, пять — шесть голов). | ||
| Строка 55: | Строка 53: | ||
==Полезные ссылки== | ==Полезные ссылки== | ||
| − | «Я не знаю ничего более прекрасного в арифметике, чем эти числа, называемые некоторыми планетарными, а другими – магическими», - писал о числах известный французский математик, один из создателей теории чисел Пьер де Ферма. Привлекающие естественной красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множества тайн. В своей жизни каждый из нас сталкивается с числами. Курс школьной программы, да и дальнейшую жизнь, трудно представить без них. | + | «Я не знаю ничего более прекрасного в арифметике, чем эти числа, называемые некоторыми планетарными, а другими – магическими», - писал о числах известный французский математик, один из создателей теории чисел Пьер де Ферма. Привлекающие естественной красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множества тайн. В своей жизни каждый из нас сталкивается с числами. Курс школьной программы, да и дальнейшую жизнь, трудно представить без них. Более подробно читаем в исследовательская работе "Магические числа": [Электронный ресурс] // Педагогический журнал "Коллеги" Интернет-портал "Детство-kz", 2017 http://collegy.ucoz.ru/publ/89-1-0-3365. (дата обращения: 20.11.2017) |
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | ||
| Строка 84: | Строка 82: | ||
*А в Греции «13» считается несчастливым днем только тогда, когда выпадает во вторник. В Италии опасаются пятницы 17-го. А вот статисты Нидерландов подсчитали, что именно 13-го числа случается меньше аварий и несчастных случаев, поскольку люди более осторожны и собраны. | *А в Греции «13» считается несчастливым днем только тогда, когда выпадает во вторник. В Италии опасаются пятницы 17-го. А вот статисты Нидерландов подсчитали, что именно 13-го числа случается меньше аварий и несчастных случаев, поскольку люди более осторожны и собраны. | ||
| − | {{center|[[Файл: | + | {{center|[[Файл:Unhappy numbers.jpg|450px]]}} |
* Числа великаны. Один из первых, кто научился называть большие числа, был древнегреческий математик Архимед. Названия были, но обозначать он их не мог. Архимед, один из гениальнейших математиков, не додумался до нуля. Впервые нуль был придуман вавилонянами примерно 2 тысячи лет назад. Однако, открытие писать нули в конце числа, было сделано в Индии полторы тысячи лет назад. Нуль был присоединен к девяти цифрам, и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно ни было. | * Числа великаны. Один из первых, кто научился называть большие числа, был древнегреческий математик Архимед. Названия были, но обозначать он их не мог. Архимед, один из гениальнейших математиков, не додумался до нуля. Впервые нуль был придуман вавилонянами примерно 2 тысячи лет назад. Однако, открытие писать нули в конце числа, было сделано в Индии полторы тысячи лет назад. Нуль был присоединен к девяти цифрам, и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно ни было. | ||
| Строка 110: | Строка 108: | ||
1000 октиллионов – 1 нониллион | 1000 октиллионов – 1 нониллион | ||
| − | {{center|[[Файл: | + | {{center|[[Файл:Gugol.png|100px]]}} - число содержащее единицу и сто нулей. |
| − | {{center|[[Файл: | + | {{center|[[Файл:Gugolplex.png|100px]]}} - число, изображаемое единицей с гуголом нулей. |
Числа гугол, гуголплекс были придуманы американским математиком Эдвардом Каснером и его племянником Милтоном Сиротта.</div> | Числа гугол, гуголплекс были придуманы американским математиком Эдвардом Каснером и его племянником Милтоном Сиротта.</div> | ||
| − | {{center|[[Файл: | + | {{center|[[Файл:Numbers_velikans.jpg]]}} |
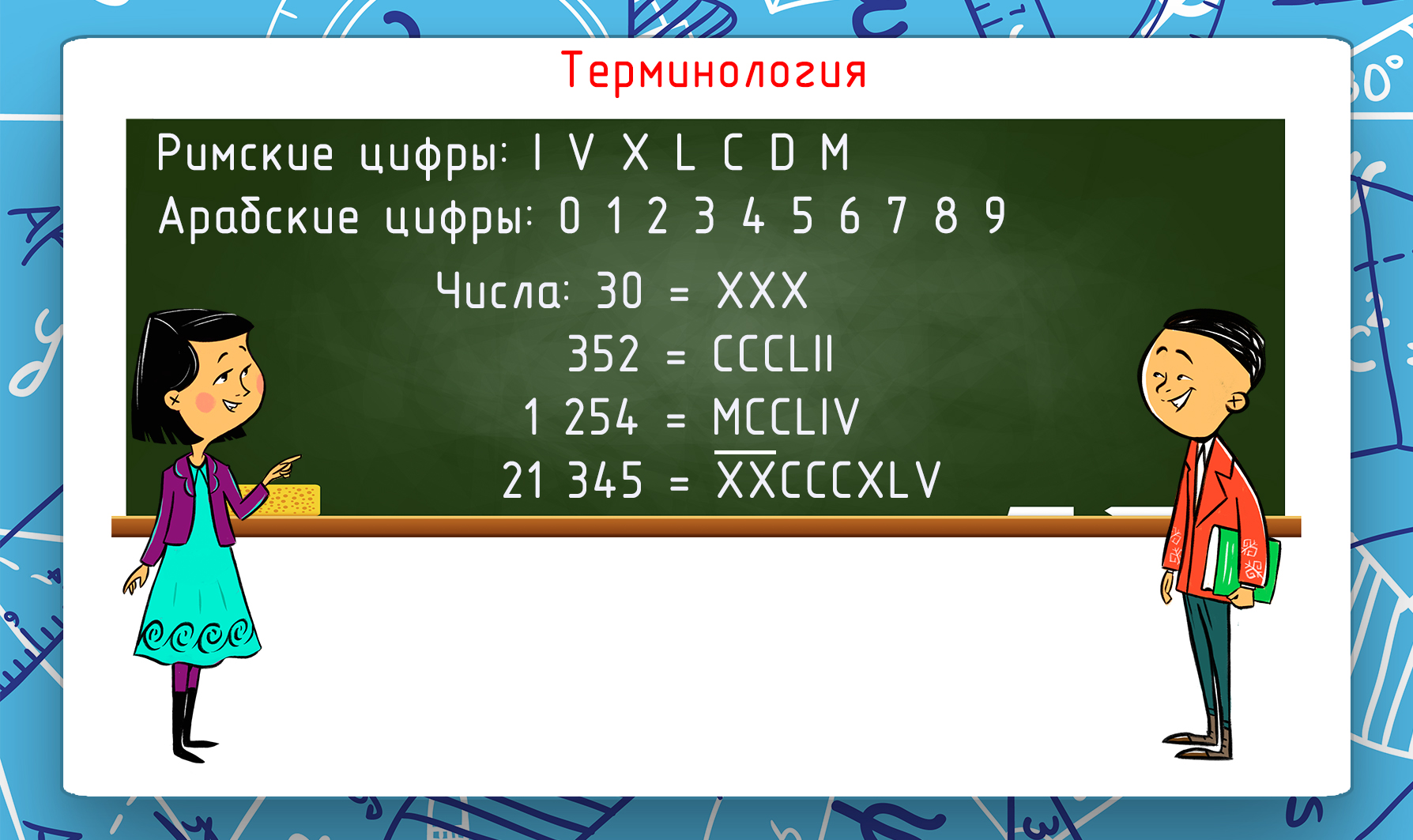
* Терминология. Термин «цифра» в переводе с арабского означает «ноль». Только со временем данное слово начали использовать для обозначения любого численного символа. | * Терминология. Термин «цифра» в переводе с арабского означает «ноль». Только со временем данное слово начали использовать для обозначения любого численного символа. | ||
| Строка 122: | Строка 120: | ||
Важно помнить, что цифры — это система знаков для записи конкретных значений чисел. Все числа состоят из цифр. Цифры и числа различных систем счисления настолько не совпадают, что число одной системы может оказаться цифрой другой, а всё потому, что это отвлечённые, выдуманные человеком понятия. | Важно помнить, что цифры — это система знаков для записи конкретных значений чисел. Все числа состоят из цифр. Цифры и числа различных систем счисления настолько не совпадают, что число одной системы может оказаться цифрой другой, а всё потому, что это отвлечённые, выдуманные человеком понятия. | ||
| − | {{center|[[Файл: | + | {{center|[[Файл:Terminology.jpg]]}} |
| Строка 134: | Строка 132: | ||
Давайте проверим, умеете ли вы правильно читать и записывать натуральные числа. В конце диктанта вас ждет приятный сюрприз. | Давайте проверим, умеете ли вы правильно читать и записывать натуральные числа. В конце диктанта вас ждет приятный сюрприз. | ||
| − | {{center|[[Файл: | + | {{center|[[Файл:Math_diktant.mp4]]}} |
</div> | </div> | ||
| Строка 146: | Строка 144: | ||
Вы уже знаете, что для записи чисел используют цифры, и когда число состоит из одной цифры, мы называем его однозначным, из двух – двузначным. Такие числа с легкостью читаем. А что делать, когда в записи больше трех цифр? Смотри и запоминай! | Вы уже знаете, что для записи чисел используют цифры, и когда число состоит из одной цифры, мы называем его однозначным, из двух – двузначным. Такие числа с легкостью читаем. А что делать, когда в записи больше трех цифр? Смотри и запоминай! | ||
| − | {{center|[[Файл: | + | {{center|[[Файл:Reading_of_natural_numbers.gif]]}} |
</div> | </div> | ||
| − | |||
<!-- четвертый элемент сайдбара лайфхак --> | <!-- четвертый элемент сайдбара лайфхак --> | ||
| Строка 158: | Строка 155: | ||
Математические фокусы — самые простые в исполнении. Для них не нужен реквизит, длительная подготовка и специальное место для демонстрации. Смысл таких фокусов — в отгадывании чисел, задуманных зрителями, или в каких-нибудь операциях над ними. Все чудеса основаны на математических закономерностях, такие фокусы можно проделывать на уроках математики. Смотрим и учимся математической магии. | Математические фокусы — самые простые в исполнении. Для них не нужен реквизит, длительная подготовка и специальное место для демонстрации. Смысл таких фокусов — в отгадывании чисел, задуманных зрителями, или в каких-нибудь операциях над ними. Все чудеса основаны на математических закономерностях, такие фокусы можно проделывать на уроках математики. Смотрим и учимся математической магии. | ||
| − | {{center|[[Файл: | + | {{center|[[Файл:5_math_fokus.mp4]]}} |
| + | </div> | ||
| + | <div class="sbstyle"> | ||
| + | <div class="row"> | ||
| + | <div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Пройди тестирование</div> | ||
| + | </div> | ||
| + | |||
| + | </div> | ||
</div> | </div> | ||
| − | |||
{{lang|:KR:Математика: Натуралдык сандар}} | {{lang|:KR:Математика: Натуралдык сандар}} | ||
[[Category:Средняя школа]] | [[Category:Средняя школа]] | ||
| − | [[Category:Математика | + | [[Category:Математика]] |
Текущая версия на 08:40, 22 октября 2018
Мы умеем выражать свои чувства, эмоции и отношение к чему-то или к кому-то с помощью слов. В разговоре, обращаясь друг с другом, мы используем слова. В математике также существует свой язык, и выражается он не только словами, но и числами. У древних людей кроме топора, сделанного из камня, и одежды из шкуры ничего не было, поэтому считать им было нечего. Со временем они стали приручать животных, обрабатывать поля, и появилась торговля. Тут уж без счёта им стало не обойтись. Сначала считали на пальцах. Когда пальцев одной руки не хватало, переходили на пальцы второй руки, а если считать нужно было дальше и пальцев обеих рук не хватало, то переходили на пальцы ног. Расширяющиеся потребности счёта заставили людей употреблять другие счётные эталоны. Так, например, для записи сравнительно большего число стала использоваться новая идея - обозначение новым знаком - зарубкой на другой палочке. С развитием письменности возможности воспроизведения числа значительно расширились. Сначала числа стали обозначаться чёрточками на материале, служащем для записи (папирус, глиняные таблички и т.д.). Затем были введены другие знаки для больших чисел. Таким образом, параллельно с развитием письменности понятие натурального числа закрепляется в устной речи и в форме обозначения специальными знаками (в письменности).
Содержание
Натуральные числа
Чисел очень много, поэтому математики разбили их на несколько групп. Самая маленькая из них – натуральные числа. С их помощью мы можем говорить о количестве предметов, а также можем назвать порядковый номер во множестве предметов. Например, мы можем сосчитать, сколько деревьев растет возле дома. А если вспомнить урок физкультуры, когда учитель просит вас рассчитаться в строю, то, наверняка, каждый из вас может без особого труда назвать свой номер.
Итак, числа, которыми мы с вами пользовались при счёте, называют натуральными числами. Обозначают их латинской буквой N.
Натуральные числа также употребляют, чтобы выразить результаты измерения различных величин: длины, площади, времени, скорости. Кроме натуральных чисел мы знаем ещё число 0 (нуль). При счёте число нуль не используется, а означает оно «ни одного». Поэтому число 0 (нуль) не является натуральным!
Системы измерения и счет у древних кыргызов
Потребность в измерении и счете родилась у кыргызов в условиях относительно высокоразвитого их общественного производства и социальной дифференциации общества. В кыргызском народе до сих пор своеобразно уживаются несколько систем счета, что свидетельствует о различных их источниках.
Древние кыргызы употребляли известные цивилизованному миру действительные математические числа и могли сосчитать членов своей семьи, домашних животных, стрелы в колчане лука, убитых или пойманных на охоте зверей, птиц.
В быту с помощью понятия «бирдин үчү» говорили о небольшом количестве предметов. Например, два — три, три — четыре, пять — шесть). Анын чакан үйүнүн төрүндө бирдин үчү болуп олтурушкан кишилер — В его маленькой юрте на почетном месте сидели несколько (немного) человек или Бирдин үчү эле малы бар — У него немного скота (три — четыре, пять — шесть голов).
В эпосе «Жаңыл Мырза» встречается старинное кыргызское слово, передающее математическое понятие количества, употребляемое при счете животных — санга.
Эки санга толуптур
Эсепсиз жылкы болуптур .
При подсчете коней
Количество их равнялось двум санга.
Поскольку данное понятие не выражало вполне конкретное, определенное количество, его использование было связано с разными трудностями, осложняло это и одновременное употребление различных систем счета. Наряду с десятичным широко было распространено двенадцатиричное (по дюжинам) исчисление, применительно к различным классам объектов, в частности, оно применялось в измерении, в основу которого было положено сравнение с известными объектами — частями тела, предметами обихода. Практическое удобство применения последнего вида измерения несомненно, однако оно было весьма приблизительным.
Глоссарий
- Число́ — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.
- Счёт — математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор, счёты и т. п.) и приспособлений (ручка, карандаш, бумага и т. п.).
- Измере́ние — совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой всеми участниками за единицу, хранящуюся в техническом средстве (средстве измерений).
Полезные ссылки
«Я не знаю ничего более прекрасного в арифметике, чем эти числа, называемые некоторыми планетарными, а другими – магическими», - писал о числах известный французский математик, один из создателей теории чисел Пьер де Ферма. Привлекающие естественной красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множества тайн. В своей жизни каждый из нас сталкивается с числами. Курс школьной программы, да и дальнейшую жизнь, трудно представить без них. Более подробно читаем в исследовательская работе "Магические числа": [Электронный ресурс] // Педагогический журнал "Коллеги" Интернет-портал "Детство-kz", 2017 http://collegy.ucoz.ru/publ/89-1-0-3365. (дата обращения: 20.11.2017)
Библиография
- Видеоурок по математике «Ряд натуральных чисел»: [Электронный ресурс] //ООО «Мультиурок», 2008-2017. URL: https://videouroki.net/blog/vidieourok-po-matiematikie-riad-natural-nykh-chisiel.html. (дата обращения: 20.11.2017)
- Энциклопедический словарь юного математика. 2-е изд., испр. и доп. - М.: Педагогика, 1989 - 352 с
- Системы измерения и счет у кыргызов.: [Электронный ресурс] //Open.kg Открытый Кыргызстан. URL: https://www.open.kg/about-kyrgyzstan/culture/ethnography/1970-sistemy-izmereniya-i-schet-u-kyrgyzov.html. (дата обращения: 20.11.2017)
- Интересные факты о цифрах и числах.: [Электронный ресурс] // Знаменитости 2014. URL: http://kvipstar.com/blog/facts/341.html. (дата обращения: 20.11.2017)
- Видео «5 простых математических фокусов»: [Электронный ресурс] // Простая математика YouTube, 2017. https://www.youtube.com/watch?v=JlgsMsnZmz8. (дата обращения: 20.11.2017)
- Учительские университеты. Исследовательская работа "Магические числа". Ростовская средняя школа
- Научное общество учащихся: [Электронный ресурс] // Педагогический журнал "Коллеги" Интернет-портал "Детство-kz", 2017 http://collegy.ucoz.ru/publ/89-1-0-3365. (дата обращения: 20.11.2017)
амые интересные факты о числах, которые не оставят вас равнодушными
- Несчастливые числа. В таких странах, как Китай, Япония и Корея число «4» считается несчастливым. Поэтому этажи с номерами, которые заканчиваются на «4» отсутствуют.
- Число «13» - во многих государствах также считается неудачным. Поэтому этаж после «12» имеет обозначение «14», «12А» или «М» (тринадцатая буква в алфавите).
- А в Греции «13» считается несчастливым днем только тогда, когда выпадает во вторник. В Италии опасаются пятницы 17-го. А вот статисты Нидерландов подсчитали, что именно 13-го числа случается меньше аварий и несчастных случаев, поскольку люди более осторожны и собраны.
- Числа великаны. Один из первых, кто научился называть большие числа, был древнегреческий математик Архимед. Названия были, но обозначать он их не мог. Архимед, один из гениальнейших математиков, не додумался до нуля. Впервые нуль был придуман вавилонянами примерно 2 тысячи лет назад. Однако, открытие писать нули в конце числа, было сделано в Индии полторы тысячи лет назад. Нуль был присоединен к девяти цифрам, и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно ни было.
1000 единиц – просто тысяча
1000 тысяч – 1 миллион
1000 миллионов – 1 биллион (или миллиард)
1000 биллионов – 1 триллион
1000 триллионов – 1 квадриллион
1000 квадриллионов - 1 квинтиллион
1000 квинтиллионов – 1 секстиллион
1000 секстиллионов – 1 септиллион
1000 септиллионов – 1октиллион
1000 октиллионов – 1 нониллион
- число содержащее единицу и сто нулей. - число, изображаемое единицей с гуголом нулей. Числа гугол, гуголплекс были придуманы американским математиком Эдвардом Каснером и его племянником Милтоном Сиротта.- Терминология. Термин «цифра» в переводе с арабского означает «ноль». Только со временем данное слово начали использовать для обозначения любого численного символа.
Важно помнить, что цифры — это система знаков для записи конкретных значений чисел. Все числа состоят из цифр. Цифры и числа различных систем счисления настолько не совпадают, что число одной системы может оказаться цифрой другой, а всё потому, что это отвлечённые, выдуманные человеком понятия.
Давайте проверим, умеете ли вы правильно читать и записывать натуральные числа. В конце диктанта вас ждет приятный сюрприз.
Вы уже знаете, что для записи чисел используют цифры, и когда число состоит из одной цифры, мы называем его однозначным, из двух – двузначным. Такие числа с легкостью читаем. А что делать, когда в записи больше трех цифр? Смотри и запоминай!
Математические фокусы — самые простые в исполнении. Для них не нужен реквизит, длительная подготовка и специальное место для демонстрации. Смысл таких фокусов — в отгадывании чисел, задуманных зрителями, или в каких-нибудь операциях над ними. Все чудеса основаны на математических закономерностях, такие фокусы можно проделывать на уроках математики. Смотрим и учимся математической магии.