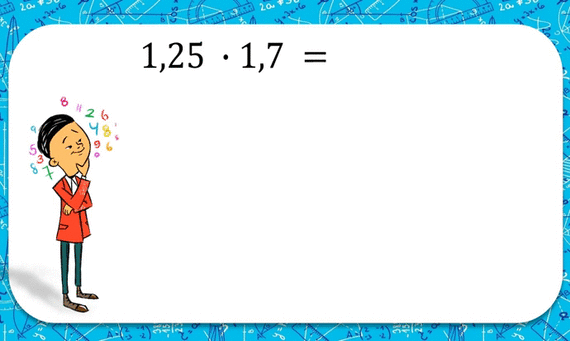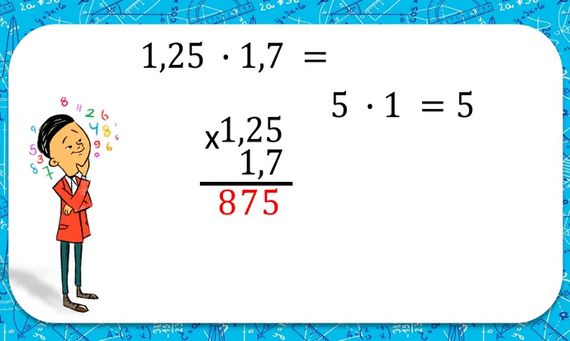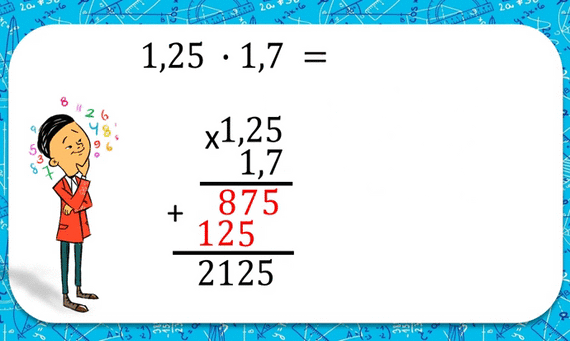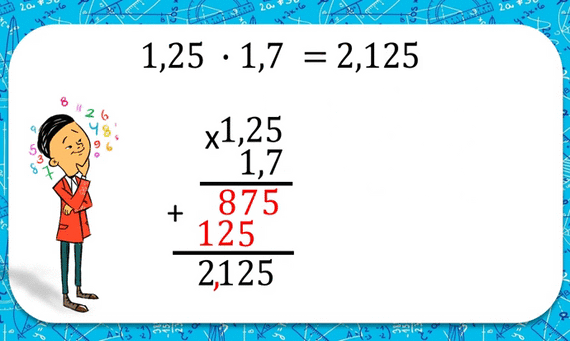БИЛИМ БУЛАГЫ

Математика: Арифметические действия над десятичными дробями — различия между версиями

(→‎Полезные ссылки)
 
(не показаны 33 промежуточные версии 2 участников)
Строка 1: Строка 1:
−
__NOTOC__
 
 
<div class="row mat-bg">
 
<div class="row mat-bg">
 
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content -->  
 
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content -->  
Строка 5: Строка 4:
  
 
Вычисления с простыми дробями становятся очень громоздкими, если знаменатели их сколько-нибудь велики. Главное затруднение состоит в приведении дробей к общему знаменателю; оно вытекает из того, что знаменатели могут быть любыми числами, в выборе которых нет никакой системы. Поэтому уже в древности пришли к мысли выбирать не произвольно, а систематически доли единицы, которые в простых дробях играют роль знаменателей.
 
Вычисления с простыми дробями становятся очень громоздкими, если знаменатели их сколько-нибудь велики. Главное затруднение состоит в приведении дробей к общему знаменателю; оно вытекает из того, что знаменатели могут быть любыми числами, в выборе которых нет никакой системы. Поэтому уже в древности пришли к мысли выбирать не произвольно, а систематически доли единицы, которые в простых дробях играют роль знаменателей.
−
<div class=”show-for-large-up”>{{center|[[Файл:Time_line.gif|800px]]}}</div>
+
{{Timeline}}
−
<div class="hide-for-large-up">{{center|[[Файл:Time_line.gif|800px]]}}</div>
+
 
 +
==Преимущество  десятичных дробей==
 
Древнейшими систематическими дробями, употреблявшимися в Вавилоне за 4000 лет до нашего времени и перешедшими через древнегреческих астрономов к астрономам Западной Европы, были шестидесятеричные дроби. В конце XVI в., когда сложные вычисления с дробями стали широко применяться во всех областях жизни, стали входить в употребление другие систематические дроби: десятичные. В них единица делится на десять долей (десятые), каждая десятая доля снова на десять долей (сотые) и т. д. Преимущество десятичных дробей перед другими систематическими состоит в том, что они основаны на той же системе, на которой построены счет и запись целых чисел. Благодаря этому и запись, и правила действий с десятичными дробями по существу те же, что и для целых чисел.
 
Древнейшими систематическими дробями, употреблявшимися в Вавилоне за 4000 лет до нашего времени и перешедшими через древнегреческих астрономов к астрономам Западной Европы, были шестидесятеричные дроби. В конце XVI в., когда сложные вычисления с дробями стали широко применяться во всех областях жизни, стали входить в употребление другие систематические дроби: десятичные. В них единица делится на десять долей (десятые), каждая десятая доля снова на десять долей (сотые) и т. д. Преимущество десятичных дробей перед другими систематическими состоит в том, что они основаны на той же системе, на которой построены счет и запись целых чисел. Благодаря этому и запись, и правила действий с десятичными дробями по существу те же, что и для целых чисел.
 
При записи десятичных дробей нет нужды обозначать наименование долей (знаменатель); это наименование узнается по месту, занимаемому соответствующей цифрой. Сначала записывается целая часть числа, справа от нее ставится запятая; первая цифра после запятой означает число десятых (т. е. десятых долей единицы), вторая — сотых, третья — тысячных и т. д. Цифры, стоящие после запятой, называются десятичными знаками.
 
При записи десятичных дробей нет нужды обозначать наименование долей (знаменатель); это наименование узнается по месту, занимаемому соответствующей цифрой. Сначала записывается целая часть числа, справа от нее ставится запятая; первая цифра после запятой означает число десятых (т. е. десятых долей единицы), вторая — сотых, третья — тысячных и т. д. Цифры, стоящие после запятой, называются десятичными знаками.
Строка 12: Строка 12:
 
<div class="blocktext">Пример. Рассмотрим дробь 7, 305. В ней содержится  семь целых, три десятых, пять тысячных (нуль показывает отсутствие сотых долей). Одним из преимуществ десятичных дробей является то, что выражение дробной части сразу прочитывается  в приведенном к одному знаменателю виде: семь целых триста пять тысячных; число  305 после запятой – это числитель дробной части, знаменателем дроби является то число, которое показывает какие доли представляет последний десятичный знак ( в данном случае 1 000). </div>
 
<div class="blocktext">Пример. Рассмотрим дробь 7, 305. В ней содержится  семь целых, три десятых, пять тысячных (нуль показывает отсутствие сотых долей). Одним из преимуществ десятичных дробей является то, что выражение дробной части сразу прочитывается  в приведенном к одному знаменателю виде: семь целых триста пять тысячных; число  305 после запятой – это числитель дробной части, знаменателем дроби является то число, которое показывает какие доли представляет последний десятичный знак ( в данном случае 1 000). </div>
  
 +
==Арифметические действия над десятичными дробями==
 
Рассмотрим, как выполняются арифметические действия над десятичными дробями.
 
Рассмотрим, как выполняются арифметические действия над десятичными дробями.
  
−
<div class=”show-for-large-up”>{{right|[[Файл:Десятичные дроби сложение действия1.jpg|500px]]}}</div>
+
{{center|[[File:Slojen 10 drob.gif|500px]]}}
−
<div class="hide-for-large-up">{{right|[[Файл:Десятичные дроби сложение действия1.jpg|500px]]}}</div>
 
  
  
Строка 27: Строка 27:
 
'''Умножение десятичных дробей.'''  
 
'''Умножение десятичных дробей.'''  
  
−
<div class=”show-for-large-up”>{{right|[[Файл:Десятичные дроби умножение1.jpg|500px]]}}</div>
+
{{right|[[File:Umnoj_drob_kyrg.gif|500px]]}}
−
<div class="hide-for-large-up">{{right|[[Файл:Десятичные дроби умножение1.jpg|500px]]}}</div>
+
 
 
Чтобы умножить одно десятичное число на другое, необходимо перемножить их как целые числа, не обращая внимания на запятые, а затем в полученном произведении отделить справа столько десятичных знаков, сколько их было вместе в обоих сомножителях. Обрати внимание, на рисунке показано, как правильно записывать умножение «столбиком».
 
Чтобы умножить одно десятичное число на другое, необходимо перемножить их как целые числа, не обращая внимания на запятые, а затем в полученном произведении отделить справа столько десятичных знаков, сколько их было вместе в обоих сомножителях. Обрати внимание, на рисунке показано, как правильно записывать умножение «столбиком».
 +
 +
  
 
<div class="blocktext">Пример. 2,064 ∙ 0,05. Перемножаем целые части 2064 ∙ 5 = 10 320. В первом сомножителе было три знака после запятой, во втором – два. В произведении число знаков после запятой должно быть пять. Отделяем их справа, получаем 0,10320. Нуль, стоящий в конце дроби, можно отбросить: 2,064 ∙ 0,05 = 0,1032.</div>
 
<div class="blocktext">Пример. 2,064 ∙ 0,05. Перемножаем целые части 2064 ∙ 5 = 10 320. В первом сомножителе было три знака после запятой, во втором – два. В произведении число знаков после запятой должно быть пять. Отделяем их справа, получаем 0,10320. Нуль, стоящий в конце дроби, можно отбросить: 2,064 ∙ 0,05 = 0,1032.</div>
 +
 
Примечание. До постановки запятой отбрасывать нули  нельзя!
 
Примечание. До постановки запятой отбрасывать нули  нельзя!
  
 
'''Деление десятичных дробей.'''
 
'''Деление десятичных дробей.'''
−
<div class=”show-for-large-up”>{{right|[[Файл:Десятичные_дроби_деление_1.jpg|500px]]}}</div>
+
 
−
<div class="hide-for-large-up">{{right|[[Файл:Десятичные_дроби_деление_1.jpg|500px]]}}</div>
+
{{right|[[File:Delen_drob.gif|500px]]}}
 +
 
 
Для деления десятичной дроби на натуральное число придерживаются следующего алгоритма:
 
Для деления десятичной дроби на натуральное число придерживаются следующего алгоритма:
 
Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую. Ставим в полученном частном запятую, когда заканчивается деление целой части делимого. Если целая часть делимого меньше делителя, то в частном ставим 0 целых. На рисунке показана запись деления «уголком».
 
Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую. Ставим в полученном частном запятую, когда заканчивается деление целой части делимого. Если целая часть делимого меньше делителя, то в частном ставим 0 целых. На рисунке показана запись деления «уголком».
Строка 42: Строка 46:
 
''Замечание.'' Возможно, что описанный процесс деления никогда не закончится. В таком случае частное нельзя точно выразить десятичной дробь, но остановившись на некоторой цифре, получим приближенный результат.
 
''Замечание.'' Возможно, что описанный процесс деления никогда не закончится. В таком случае частное нельзя точно выразить десятичной дробь, но остановившись на некоторой цифре, получим приближенный результат.
  
 +
==Основные свойства десятичных дробей==
 
Из вышесказанного можно сказать, что десятичные дроби - это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить. Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит ваш успех. Несомненно, вы знаете, как все это делать, но на всякий случай, для удобства действий над дробями предлагаем запомнить основные свойства десятичных дробей. Они очень простые, мы собрали их в небольшую памятку. Скачайте, распечатайте и пользуйтесь!
 
Из вышесказанного можно сказать, что десятичные дроби - это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить. Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит ваш успех. Несомненно, вы знаете, как все это делать, но на всякий случай, для удобства действий над дробями предлагаем запомнить основные свойства десятичных дробей. Они очень простые, мы собрали их в небольшую памятку. Скачайте, распечатайте и пользуйтесь!
−
<div class=”show-for-large-up”>{{center|[[Файл:Десятичные_дроби_свойства_1.jpg|800px]]}}</div>
+
 
−
<div class="hide-for-large-up">{{center|[[Файл:Десятичные_дроби_свойства_1.jpg|800px]]}}</div>
+
{{center|[[File:Pravila_drob.jpg|800px]]}}
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
 +
==Примеры==
 +
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 +
  <li class="active">
 +
    [[file:Example_1_drob.gif|300px]]
 +
  </li>
 +
<li>
 +
    [[file:Example_2_drob.gif|300px]]
 +
  </li>
 +
<li>
 +
    [[file:Example_3_drob.gif|300px]]
 +
  </li>
 +
</ul>
 +
 
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
 
==Глоссарий==
 
==Глоссарий==
 +
 
'''Целые числа''' – это натуральные числа, а также противоположные им числа и нуль
 
'''Целые числа''' – это натуральные числа, а также противоположные им числа и нуль
  
−
==Примеры==
+
'''Доля''' — качественно или количественно выраженная часть от чего-нибудь целого
−
<div class=”show-for-large-up”>{{center|[[Файл:Пример_1_десятичные_дроби.gif|800px]]}}</div>
+
 
−
<div class="hide-for-large-up">{{center|[[Файл:Пример_1_десятичные_дроби.gif|800px]]}}</div>
+
'''Проце́нт''' (лат. per cent «на сотню; сотая») — сотая часть; обозначается знаком «%»; используется для обозначения доли чего-либо по отношению к целому.
−
<br>
+
 
−
<div class=”show-for-large-up”>{{center|[[Файл:Пример_2_десятичные_дроби.gif|800px]]}}</div>
+
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
−
<div class="hide-for-large-up">{{center|[[Файл:Пример_1_десятичные_дроби.gif|800px]]}}</div>
+
 
−
<br>
+
==Полезные ссылки==
−
<div class=”show-for-large-up”>{{center|[[Файл:Пример_3_десятичные_дроби.gif|800px]]}}</div>
+
 
−
<div class="hide-for-large-up">{{center|[[Файл:Пример_1_десятичные_дроби.gif|800px]]}}</div>
+
Среди десятичных дробей особенно часто на практике используется дробь 0,01, которая называется процентом и обозначается 1 %. Понимание и умение производить процентные расчёты необходимы для каждого. Ведь почти во всех областях человеческой деятельности встречаются проценты. Без этого понятия нельзя обойтись ни в бухгалтерии, ни в финансовом деле, ни в статистике. Чтобы начислить зарплату работнику, нужно знать процент налоговых отчислений; чтобы открыть счёт в сбербанке или взять кредит, нас интересует размер процентных начислений на сумму вклада и процент по кредиту. В торговле понятие «процент» используется наиболее часто. Мы очень часто можем слышать о скидках, наценках, уценках, прибыли, и т.д. – всё это проценты. Современному человеку необходимо хорошо ориентироваться в большом потоке информации, принимать правильные решения в разных жизненных ситуациях. Для этого необходимо хорошо производить процентные расчёты. Более подробно о том, как решать такие задачи, узнать можно здесь:  Задачи на проценты. : [Электронный ресурс] // «Сёзнайка.ру», 2015. URL:  http://www.seznaika.ru/matematika/ege/114-2009-12-06-18-08-29 (дата обращения: 20. 11. 2017)
 +
 
 +
Комикс – это сильно сказано. Новая книга всемирно знаменитого карикатуриста Ларри Гоника, изучавшего и преподававшего математику в Гарвардском университете, представляет собой интенсивный курс алгебры, охватывающий ряд основных тем школьной программы. С живым юмором автор делает экскурс в историю алгебры и приводит многочисленные примеры практического применения «царицы наук» в современной жизни. Уникальная способность Гоника преподносить сложный материал весело, интересно и легко для восприятия, да еще и в безупречно ясном, структурированном виде, делает эту книгу отличным пособием для школьников, а также для всех желающих поддержать в форме свои математические способности.: Алгебра. Естественная наука в комиксах. Ларри Гоник.:[Электронный ресурс] //Братчикова Надежда Владимировна, 2016-2017. URL:http://mathlife.ru/algebra . (дата обращения: 20. 11. 2017)
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
  
 
== Библиография ==
 
== Библиография ==
Строка 75: Строка 104:
 
</div>
 
</div>
 
<span class="firstcharacter">Д</span><p align="justify">есятичные  дроби впервые появились в Китае. В Поднебесной империи их стали использовать примерно с III века до нашей эры. История десятичных дробей началась с китайского математика Лю Хуэя, предложившего использовать их при извлечении квадратных корней.  
 
<span class="firstcharacter">Д</span><p align="justify">есятичные  дроби впервые появились в Китае. В Поднебесной империи их стали использовать примерно с III века до нашей эры. История десятичных дробей началась с китайского математика Лю Хуэя, предложившего использовать их при извлечении квадратных корней.  
−
<div class=”show-for-large-up”>{{center|[[Файл:Лю_Хуэй_китайский.jpg|400px]]}}</div>
+
{{center|[[Файл:Математика_в_9_томах_с_комментарием_Лю_Хуэя.jpg]]}}
−
<div class="hide-for-large-up">{{center|[[Файл:Лю_Хуэй_китайский.jpg|400px]]}}</div>
 
  
 
В III веке нашей эры десятичные дроби в Китае стали применяться при расчете веса и объема. Постепенно они все глубже начали проникать в математику. В Европе, однако, десятичные дроби стали использоваться гораздо позже.  
 
В III веке нашей эры десятичные дроби в Китае стали применяться при расчете веса и объема. Постепенно они все глубже начали проникать в математику. В Европе, однако, десятичные дроби стали использоваться гораздо позже.  
 
Независимо от китайских предшественников десятичные дроби открыл астроном аль-Каши из древнего города Самарканда. Жил и трудился он в XV веке. Свою теорию ученый изложил в трактате «Ключ к арифметике», увидевшем свет в 1427 году. Аль-Каши предложил использовать новую форму записи дробей. И целая, и дробная часть теперь писались в одной строке. Для их разделения самаркандский астроном не использовал запятую. Он писал целое число и дробную часть разными цветами, используя черные и красные чернила. Иногда для разделения аль-Каши также применял вертикальную черту.  
 
Независимо от китайских предшественников десятичные дроби открыл астроном аль-Каши из древнего города Самарканда. Жил и трудился он в XV веке. Свою теорию ученый изложил в трактате «Ключ к арифметике», увидевшем свет в 1427 году. Аль-Каши предложил использовать новую форму записи дробей. И целая, и дробная часть теперь писались в одной строке. Для их разделения самаркандский астроном не использовал запятую. Он писал целое число и дробную часть разными цветами, используя черные и красные чернила. Иногда для разделения аль-Каши также применял вертикальную черту.  
−
<div class=”show-for-large-up”>{{center|[[Файл:Ученые_десятичные_дроби_каши___.jpg|400px]]}}</div>
+
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
−
<div class="hide-for-large-up">{{center|[[Файл:Ученые_десятичные_дроби_каши___.jpg|400px]]}}</div>
+
  <li class="active">
 +
    [[file:Руководство по арифметике и геометрии аль-Каши (около 1436 г.).JPG]]
 +
  </li>
 +
<li>
 +
    [[file:Страница_рукописи_вычисления_числа_π_аль-Каши.jpg]]
 +
  </li>
 +
</ul>
 +
 
 
Новый вид дробей начал появляться в трудах европейских математиков с XIII века. Нужно заметить, что с трудами аль-Каши, как и с изобретением китайцев они знакомы не были. Десятичные дроби появились в трудах Иордана Неморария. Затем их использовал уже в XVI веке Франсуа Виет. Французский ученый написал «Математический канон», в котором содержались тригонометрические таблицы. В них Виет использовал десятичные дроби. Для разделения целой и дробной части ученый применял вертикальную черту, а также разный размер шрифта. Однако это были лишь частные случаи научного использования.
 
Новый вид дробей начал появляться в трудах европейских математиков с XIII века. Нужно заметить, что с трудами аль-Каши, как и с изобретением китайцев они знакомы не были. Десятичные дроби появились в трудах Иордана Неморария. Затем их использовал уже в XVI веке Франсуа Виет. Французский ученый написал «Математический канон», в котором содержались тригонометрические таблицы. В них Виет использовал десятичные дроби. Для разделения целой и дробной части ученый применял вертикальную черту, а также разный размер шрифта. Однако это были лишь частные случаи научного использования.
−
<div class=”show-for-large-up”>{{center|[[Файл:Ученые_десятичные_дроби_Симон_Стивен_.jpg|400px]]}}</div>
+
{{center|[[Файл:Титульный_лист_издания_Десятой_Симона_Стевина.jpg]]}}
−
<div class="hide-for-large-up">{{center|[[Файл:Ученые_десятичные_дроби_Симон_Стивен_.jpg|400px]]}}</div>
 
 
Для решения повседневных задач десятичные дроби в Европе стали применяться несколько позже. Произошло это благодаря голландскому ученому Симону Стевину в конце XVI века. Он издал математический труд «Десятая» в 1585 году. В нем ученый изложил теорию использования десятичных дробей в арифметике, в денежной системе и для определения мер и весов.  
 
Для решения повседневных задач десятичные дроби в Европе стали применяться несколько позже. Произошло это благодаря голландскому ученому Симону Стевину в конце XVI века. Он издал математический труд «Десятая» в 1585 году. В нем ученый изложил теорию использования десятичных дробей в арифметике, в денежной системе и для определения мер и весов.  
−
<div class=”show-for-large-up”>{{center|[[Файл:Ученые_десятичные_дроби_виет.jpg|400px]]}}</div>
+
{{center|[[Файл:Франсуа_Виет_Опера_Математике.jpg]]}}
−
<div class="hide-for-large-up">{{center|[[Файл:Ученые_десятичные_дроби_виет.jpg|400px]]}}</div>
 
 
Стевин также не пользовался запятой. Он для ясности указывал над каждой цифрой (или после неё) заключённый в кружок её номер разряда.  
 
Стевин также не пользовался запятой. Он для ясности указывал над каждой цифрой (или после неё) заключённый в кружок её номер разряда.  
 
Впервые запятая разделила две части десятичной дроби только в 1592 году. В Англии, однако, вместо нее стали применять точку. На территории США до сих пор десятичные дроби пишут именно таким образом. Одним из инициаторов использования обоих знаков препинания для разделения целой и дробной части был шотландский математик Джон Непер. Он высказал свое предложение в 1617 году. Запятой пользовался и немецкий ученый Иоганн Кеплер.   
 
Впервые запятая разделила две части десятичной дроби только в 1592 году. В Англии, однако, вместо нее стали применять точку. На территории США до сих пор десятичные дроби пишут именно таким образом. Одним из инициаторов использования обоих знаков препинания для разделения целой и дробной части был шотландский математик Джон Непер. Он высказал свое предложение в 1617 году. Запятой пользовался и немецкий ученый Иоганн Кеплер.   
−
<div class=”show-for-large-up”>{{center|[[Файл:В_разные_времена_обозначение__десятичных_дробей__.jpg|400px]]}}</div>
+
{{center|[[Файл:Обозначение десятичных дробей .jpg]]}}
−
<div class="hide-for-large-up">{{center|[[Файл:В_разные_времена_обозначение__десятичных_дробей__.jpg|400px]]}}</div>
+
Полная теория дробей, мало чем отличающаяся от современной, была изложена в первом учебнике по арифметике, написанном в 1701 году Леонтием Филипповичем Магницким. «Арифметика» состояла из нескольких частей. О дробях подробно автор рассказывает в разделе «О числах ломаных или с долями». Магницкий приводит операции с «ломанными» числами, разные их обозначения.</p>
−
Полная теория дробей, мало чем отличающаяся от современной, была изложена в первом учебнике по арифметике, написанном в 1701 году Леонтием Филипповичем Магницким. «Арифметика» состояла из нескольких частей. О дробях подробно автор рассказывает в разделе «О числах ломаных или с долями». Магницкий приводит операции с «ломанными» числами, разные их обозначения..</p>
+
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
−
<div class=”show-for-large-up”>{{center|[[Файл:Ученые десятичные дроби Магницкий .jpg|400px]]}}</div>
+
  <li class="active">
−
<div class="hide-for-large-up">{{center|[[Файл:Ученые десятичные дроби Магницкий .jpg|400px]]}}</div>
+
    [[file:Арифметика_Магницкого_Издание_1914.jpg]]
 +
  </li>
 +
<li>
 +
    [[file:Арифметика Магницкого Издание 1914111.jpg]]
 +
  </li>
 +
<li>
 +
    [[file:Арифметика Магницкого Издание -19141222.jpg]]
 +
  </li>
 +
</ul>
 +
 
 
<div class="row">
 
<div class="row">
 
<div class="large-9 medium-5 small-9 large-centered medium-centered small-centered columns style="text-align:center; text-indent:0px;"></div>
 
<div class="large-9 medium-5 small-9 large-centered medium-centered small-centered columns style="text-align:center; text-indent:0px;"></div>
Строка 109: Строка 151:
 
Порой бывает, учишь-учишь, а правила никак не запоминаются. Предлагаем небольшие стихотворения, которые помогут справится с умножением и делением десятичных дробей.
 
Порой бывает, учишь-учишь, а правила никак не запоминаются. Предлагаем небольшие стихотворения, которые помогут справится с умножением и делением десятичных дробей.
  
−
<div class=”show-for-large-up”>{{center|[[Файл:Лайфхак_дроби_десятичные_дроби.jpg|450px]]}}</div>
+
{{center|[[Файл:Деление и умножение десятичных дробей.jpg]]}}
−
<div class="hide-for-large-up">{{center|[[Файл:Лайфхак_дроби_десятичные_дроби.jpg|450px]]}}</div>
 
 
</div>
 
</div>
  
−
<!-- четвертый элемент сайдбара викторины игры тесты -->
+
<div class="sbstyle">
−
<div class="shadow  radius sbstyle" style="margin-top:20px;">
 
−
 
 
 
<div class="row">
 
<div class="row">
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">[[Файл:Mzm.usttsidx.png|100px]]</div>
+
<div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Пройди тестирование</div>
−
</div>
 
−
Попробуйте ответить правильно на пять вопросов:
 
−
<quiz display = simple shuffleanswers=true >
 
−
{ Запишите в виде десятичной дроби число    [[Файл:3_._5.png|50px]].
 
−
|type="()"}
 
−
+ 0,6
 
−
- 0,8
 
−
- 0,75
 
−
 
 
−
{ Запишите в виде десятичной дроби число    [[Файл:5.11.16.png|50px]].
 
−
|type="()"}
 
−
- 5,5875
 
−
+ 5,6875
 
−
- 5,7675
 
−
 
 
−
{ Запишите в виде десятичной дроби частное:  11 : 10.
 
−
|type="()"}
 
−
- 11
 
−
+ 1,1
 
−
- 1,2
 
−
 
 
−
{ Выполните действия:  9,83 + 2,9 ∙ 7,6.
 
−
 
 
−
|type="()"}
 
−
+ 31,87
 
−
- 32
 
−
- 31,4
 
−
 
 
−
{ 5. Выполните действия:  72,072 : 6,3 + 1,9.
 
−
 
 
−
|type="()"}
 
−
- 13,3
 
−
+ 13,34
 
−
- 12,34
 
−
</quiz>
 
 
</div>
 
</div>
 +
 
</div>
 
</div>
 
</div>
 
</div>
Строка 159: Строка 164:
 
{{lang|:KR:Математика: Ондук бөлчөктөрдөгү арифметикалык амалдар}}
 
{{lang|:KR:Математика: Ондук бөлчөктөрдөгү арифметикалык амалдар}}
 
[[Category:Средняя школа]]
 
[[Category:Средняя школа]]
−
[[Category:Математика: Ондук бөлчөктөрдөгү арифметикалык амалдар]]
+
[[Category:Математика]]

Текущая версия на 08:43, 22 октября 2018

Вычисления с простыми дробями становятся очень громоздкими, если знаменатели их сколько-нибудь велики. Главное затруднение состоит в приведении дробей к общему знаменателю; оно вытекает из того, что знаменатели могут быть любыми числами, в выборе которых нет никакой системы. Поэтому уже в древности пришли к мысли выбирать не произвольно, а систематически доли единицы, которые в простых дробях играют роль знаменателей.

  • Китайский математик Лю Хуэй

    Лю Хуэй

    Лю Хуэй — китайский математик. Жил в царстве Вэй в эпоху троецарствия. Известен своими комментариями на «Математику в девяти книгах» (Цзю чжан суаньшу), которая представляет собой сборник решений математических задач из повседневной жизни. Лю Хуэй опубликовал «Цзю чжан суаньшу» в 263 году со своими комментариями, это старейшая сохранившаяся публикация книги.

  • Китайский математик и астроном Цзу Чун-чжи

    Чун – Чжи

    Чун – Чжи (429—500) — китайский математик и астроном.

    Один из самых знаменитых китайских ученых, математик, астроном, инженер, механик и литератор.

    Первым в мире рассчитал число π с точностью до седьмого знака после запятой, дав его значение между 3,1415926 и 3,1415927; более точное значение было вычислено лишь тысячу лет спустя.

  • Персидский учёный Аль-Бируни

    Аль-Бируни

    Средневековый персидский учёный-энциклопедист и мыслитель, автор многочисленных капитальных трудов по истории, географии, филологии, астрономии, математике, механике, геодезии, минералогии, фармакологии, геологии и др. Бируни владел почти всеми науками своего времени. Уделял много внимания математике, особенно тригонометрии: помимо значительной части «Канона Мас‘уда», он посвятил ей сочинения «Об определении хорд в круге при помощи вписанной в него ломаной линии».

  • Аль – Каши – один из крупнейших математиков и астрономов XV века

    Аль – Каши

    Один из крупнейших математиков и астрономов XV века, сотрудник Улугбека, один из руководителей Самаркандской обсерватории.

    В трактате «Ключ арифметики» он вводит десятичные дроби, формулирует основные правила действия с ними и приводит способы перевода шестидесятеричных дробей в десятичные и обратно.

  • Франсуа Виет, сеньор де ля Биготьер — французский математик, основоположник символической алгебры

    Франсуа Виет

    Франсуа Виет, сеньор де ля Биготьер — французский математик, основоположник символической алгебры. Научные заслуги Виета:

    Знаменитые «формулы Виета» для коэффициентов многочлена как функций его корней.

    Новый тригонометрический метод решения неприводимого кубического уравнения.

  • Христофор Клавий – германский математик и астроном

    Христофор Клавий

    Христофор Клавий – германский математик и астроном. В 1574 году он издал и прокомментировал «Начала» Евклида, а в 1608 году написал учебник по алгебре. Изложил полную теорию дробей и операций над ними.

  • Джованни Антонио Маджини – итальянский картограф, астроном и математик

    Джованни Антонио Маджини

    Джованни Антонио Маджини – итальянский картограф, астроном и математик.

    Маджини первым предложил использовать запятую в качестве разделителя целой и дробной части десятичных дробей.В честь учёного назван лунный кратер на видимой стороне Луны.

  • Джон Непер – шотландский математик

    Джон Непер

    Джон Непер – шотландский математик, один из изобретателей логарифмов, первый публикатор логарифмических таблиц, астроном. В 1614 году Непер опубликовал в Эдинбурге сочинение под названием «Описание удивительной таблицы логарифмов». В его работах можно было увидеть систематическое использование десятичной точки для отделения дробной части чисел от целой.

  • Симон Стевин – фламандский математик

    Симон Стевин

    Симон Стевин – фламандский математик, механик и инженер. Известен своей книгой «Десятая» (De Thiende), изданной на фламандском и французском языках в 1585 г.

    В своем труде он показал практическое описание арифметики десятичных дробей, а также пылкую и хорошо аргументированную пропаганду полезности их применения, в частности, в системах мер и монетном деле.

  • Иоганн Кеплер – немецкий математик

    Иоганн Кеплер

    Иоганн Кеплер - немецкий математик, астроном, механик, оптик. Нашёл способ определения объёмов разнообразных тел вращения, использовал метод интегрального исчисления. Ввел термин среднее арифметическое.

  • Леонтий Филиппович Магницкий - русский математик

    Леонтий Магницкий

    Леонтий Филиппович Магницкий - русский математик, педагог. Преподаватель математики в Школе математических и навигацких наук в Москве, автор первого в России учебного пособия по математике.

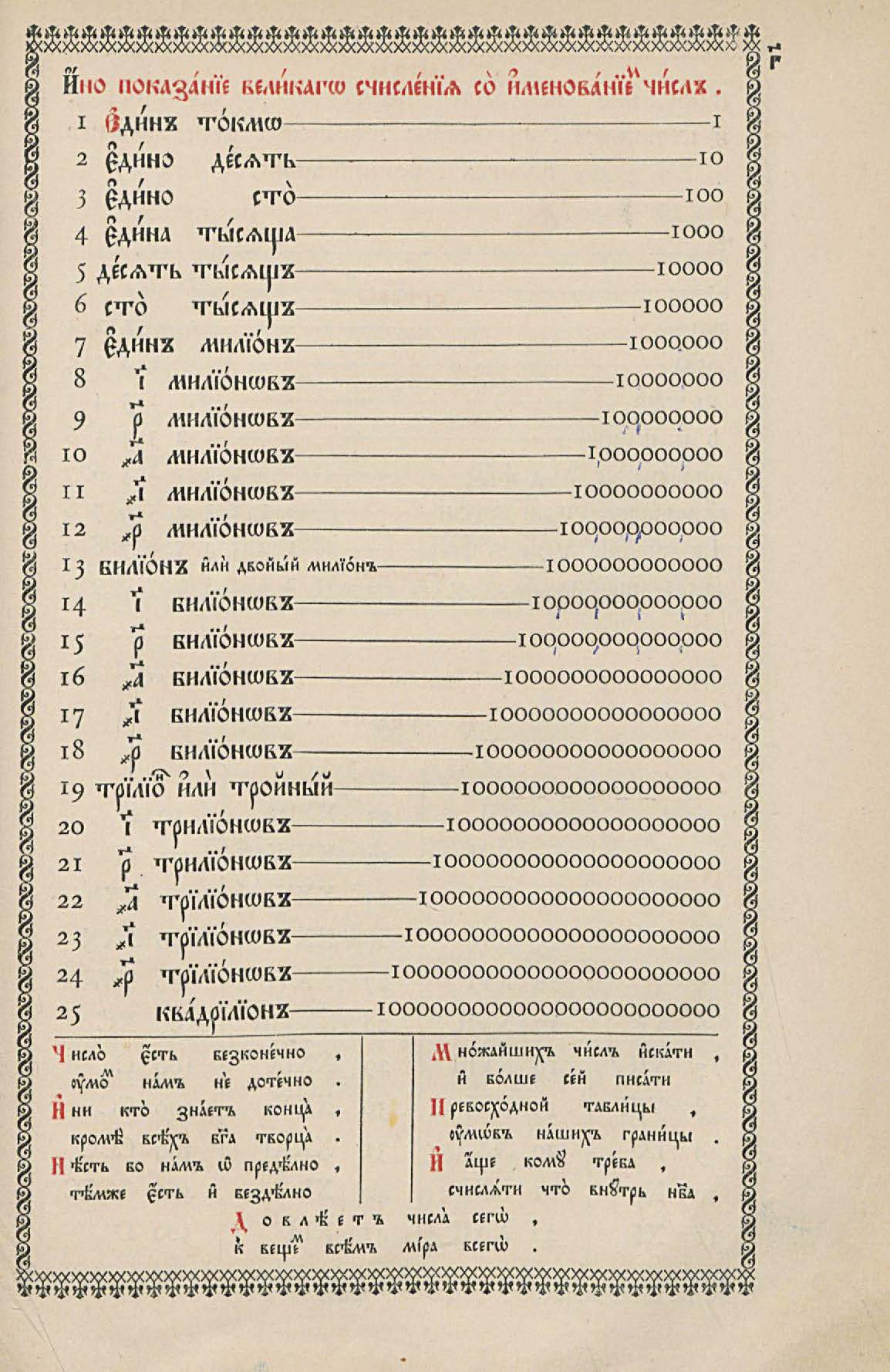
    Введённые им в русский язык математические термины: множитель, делитель, произведение, извлечение корня, миллион, биллион, триллион, квадриллион, знаменатель, дробь.

Преимущество десятичных дробей

Древнейшими систематическими дробями, употреблявшимися в Вавилоне за 4000 лет до нашего времени и перешедшими через древнегреческих астрономов к астрономам Западной Европы, были шестидесятеричные дроби. В конце XVI в., когда сложные вычисления с дробями стали широко применяться во всех областях жизни, стали входить в употребление другие систематические дроби: десятичные. В них единица делится на десять долей (десятые), каждая десятая доля снова на десять долей (сотые) и т. д. Преимущество десятичных дробей перед другими систематическими состоит в том, что они основаны на той же системе, на которой построены счет и запись целых чисел. Благодаря этому и запись, и правила действий с десятичными дробями по существу те же, что и для целых чисел. При записи десятичных дробей нет нужды обозначать наименование долей (знаменатель); это наименование узнается по месту, занимаемому соответствующей цифрой. Сначала записывается целая часть числа, справа от нее ставится запятая; первая цифра после запятой означает число десятых (т. е. десятых долей единицы), вторая — сотых, третья — тысячных и т. д. Цифры, стоящие после запятой, называются десятичными знаками.

Пример. Рассмотрим дробь 7, 305. В ней содержится семь целых, три десятых, пять тысячных (нуль показывает отсутствие сотых долей). Одним из преимуществ десятичных дробей является то, что выражение дробной части сразу прочитывается в приведенном к одному знаменателю виде: семь целых триста пять тысячных; число 305 после запятой – это числитель дробной части, знаменателем дроби является то число, которое показывает какие доли представляет последний десятичный знак ( в данном случае 1 000).

Арифметические действия над десятичными дробями

Рассмотрим, как выполняются арифметические действия над десятичными дробями.

Slojen 10 drob.gif


При сложении и вычитании десятичных дробей поступают следующим образом:

1. При необходимости уравнивают количество знаков после запятой, добавляя справа нули к соответствующей дроби, что, согласно основному свойству десятичных дробей, не влияет на величину дроби.
2. Записывают дроби так, чтобы их запятые находились друг под другом (или, что, то же самое, разряд под разрядом).
3. Сложить/вычесть, не обращая внимания на запятую, как целые числа. Складываем по одной цифре, начиная с самого крайнего правого разряда и двигаясь влево к следующему.
4. Поставить запятую в сумме/разности под запятыми, складываемых/вычитаемых дробей.

Умножение десятичных дробей.

Umnoj drob kyrg.gif

Чтобы умножить одно десятичное число на другое, необходимо перемножить их как целые числа, не обращая внимания на запятые, а затем в полученном произведении отделить справа столько десятичных знаков, сколько их было вместе в обоих сомножителях. Обрати внимание, на рисунке показано, как правильно записывать умножение «столбиком».


Пример. 2,064 ∙ 0,05. Перемножаем целые части 2064 ∙ 5 = 10 320. В первом сомножителе было три знака после запятой, во втором – два. В произведении число знаков после запятой должно быть пять. Отделяем их справа, получаем 0,10320. Нуль, стоящий в конце дроби, можно отбросить: 2,064 ∙ 0,05 = 0,1032.

Примечание. До постановки запятой отбрасывать нули нельзя!

Деление десятичных дробей.

Delen drob.gif

Для деления десятичной дроби на натуральное число придерживаются следующего алгоритма: Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую. Ставим в полученном частном запятую, когда заканчивается деление целой части делимого. Если целая часть делимого меньше делителя, то в частном ставим 0 целых. На рисунке показана запись деления «уголком».

Замечание. Возможно, что описанный процесс деления никогда не закончится. В таком случае частное нельзя точно выразить десятичной дробь, но остановившись на некоторой цифре, получим приближенный результат.

Основные свойства десятичных дробей

Из вышесказанного можно сказать, что десятичные дроби - это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить. Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит ваш успех. Несомненно, вы знаете, как все это делать, но на всякий случай, для удобства действий над дробями предлагаем запомнить основные свойства десятичных дробей. Они очень простые, мы собрали их в небольшую памятку. Скачайте, распечатайте и пользуйтесь!

Pravila drob.jpg
В начало

Примеры

  • Example 1 drob.gif
  • Example 2 drob.gif
  • Example 3 drob.gif


В начало

Глоссарий

Целые числа – это натуральные числа, а также противоположные им числа и нуль

Доля — качественно или количественно выраженная часть от чего-нибудь целого

Проце́нт (лат. per cent «на сотню; сотая») — сотая часть; обозначается знаком «%»; используется для обозначения доли чего-либо по отношению к целому.

В начало

Полезные ссылки

Среди десятичных дробей особенно часто на практике используется дробь 0,01, которая называется процентом и обозначается 1 %. Понимание и умение производить процентные расчёты необходимы для каждого. Ведь почти во всех областях человеческой деятельности встречаются проценты. Без этого понятия нельзя обойтись ни в бухгалтерии, ни в финансовом деле, ни в статистике. Чтобы начислить зарплату работнику, нужно знать процент налоговых отчислений; чтобы открыть счёт в сбербанке или взять кредит, нас интересует размер процентных начислений на сумму вклада и процент по кредиту. В торговле понятие «процент» используется наиболее часто. Мы очень часто можем слышать о скидках, наценках, уценках, прибыли, и т.д. – всё это проценты. Современному человеку необходимо хорошо ориентироваться в большом потоке информации, принимать правильные решения в разных жизненных ситуациях. Для этого необходимо хорошо производить процентные расчёты. Более подробно о том, как решать такие задачи, узнать можно здесь: Задачи на проценты. : [Электронный ресурс] // «Сёзнайка.ру», 2015. URL: http://www.seznaika.ru/matematika/ege/114-2009-12-06-18-08-29 (дата обращения: 20. 11. 2017)

Комикс – это сильно сказано. Новая книга всемирно знаменитого карикатуриста Ларри Гоника, изучавшего и преподававшего математику в Гарвардском университете, представляет собой интенсивный курс алгебры, охватывающий ряд основных тем школьной программы. С живым юмором автор делает экскурс в историю алгебры и приводит многочисленные примеры практического применения «царицы наук» в современной жизни. Уникальная способность Гоника преподносить сложный материал весело, интересно и легко для восприятия, да еще и в безупречно ясном, структурированном виде, делает эту книгу отличным пособием для школьников, а также для всех желающих поддержать в форме свои математические способности.: Алгебра. Естественная наука в комиксах. Ларри Гоник.:[Электронный ресурс] //Братчикова Надежда Владимировна, 2016-2017. URL:http://mathlife.ru/algebra . (дата обращения: 20. 11. 2017)

В начало


Библиография

  • М. Я. Выгодский. Справочник по элементарной математике. Москва 1986.
  • Задачи на проценты. : [Электронный ресурс] // «Сёзнайка.ру», 2015. URL: http://www.seznaika.ru/matematika/ege/114-2009-12-06-18-08-29 (дата обращения: 20. 11. 2017)
  • Дроби: история дробей. История возникновения обыкновенных дробей.: [Электронный ресурс] // «ФБ», 2017 URL: http://fb.ru/article/236507/drobi-istoriya-drobey-istoriya-vozniknoveniya-obyiknovennyih-drobey (дата обращения: 20. 11. 2017)
  • Алгебра. Естественная наука в комиксах. Ларри Гоник.:[Электронный ресурс] //Братчикова Надежда Владимировна, 2016-2017. URL:http://mathlife.ru/algebra . (дата обращения: 20. 11. 2017)
В начало
Из истории дробей
Д

есятичные дроби впервые появились в Китае. В Поднебесной империи их стали использовать примерно с III века до нашей эры. История десятичных дробей началась с китайского математика Лю Хуэя, предложившего использовать их при извлечении квадратных корней.

Математика в 9 томах с комментарием Лю Хуэя.jpg

В III веке нашей эры десятичные дроби в Китае стали применяться при расчете веса и объема. Постепенно они все глубже начали проникать в математику. В Европе, однако, десятичные дроби стали использоваться гораздо позже. Независимо от китайских предшественников десятичные дроби открыл астроном аль-Каши из древнего города Самарканда. Жил и трудился он в XV веке. Свою теорию ученый изложил в трактате «Ключ к арифметике», увидевшем свет в 1427 году. Аль-Каши предложил использовать новую форму записи дробей. И целая, и дробная часть теперь писались в одной строке. Для их разделения самаркандский астроном не использовал запятую. Он писал целое число и дробную часть разными цветами, используя черные и красные чернила. Иногда для разделения аль-Каши также применял вертикальную черту.

  • Руководство по арифметике и геометрии аль-Каши (около 1436 г.).JPG
  • Страница рукописи вычисления числа π аль-Каши.jpg

Новый вид дробей начал появляться в трудах европейских математиков с XIII века. Нужно заметить, что с трудами аль-Каши, как и с изобретением китайцев они знакомы не были. Десятичные дроби появились в трудах Иордана Неморария. Затем их использовал уже в XVI веке Франсуа Виет. Французский ученый написал «Математический канон», в котором содержались тригонометрические таблицы. В них Виет использовал десятичные дроби. Для разделения целой и дробной части ученый применял вертикальную черту, а также разный размер шрифта. Однако это были лишь частные случаи научного использования.

Титульный лист издания Десятой Симона Стевина.jpg

Для решения повседневных задач десятичные дроби в Европе стали применяться несколько позже. Произошло это благодаря голландскому ученому Симону Стевину в конце XVI века. Он издал математический труд «Десятая» в 1585 году. В нем ученый изложил теорию использования десятичных дробей в арифметике, в денежной системе и для определения мер и весов.

Франсуа Виет Опера Математике.jpg

Стевин также не пользовался запятой. Он для ясности указывал над каждой цифрой (или после неё) заключённый в кружок её номер разряда. Впервые запятая разделила две части десятичной дроби только в 1592 году. В Англии, однако, вместо нее стали применять точку. На территории США до сих пор десятичные дроби пишут именно таким образом. Одним из инициаторов использования обоих знаков препинания для разделения целой и дробной части был шотландский математик Джон Непер. Он высказал свое предложение в 1617 году. Запятой пользовался и немецкий ученый Иоганн Кеплер.

Обозначение десятичных дробей .jpg
Полная теория дробей, мало чем отличающаяся от современной, была изложена в первом учебнике по арифметике, написанном в 1701 году Леонтием Филипповичем Магницким. «Арифметика» состояла из нескольких частей. О дробях подробно автор рассказывает в разделе «О числах ломаных или с долями». Магницкий приводит операции с «ломанными» числами, разные их обозначения.

  • Арифметика Магницкого Издание 1914.jpg
  • Арифметика Магницкого Издание 1914111.jpg
  • Арифметика Магницкого Издание -19141222.jpg
Запоминаем легко

Порой бывает, учишь-учишь, а правила никак не запоминаются. Предлагаем небольшие стихотворения, которые помогут справится с умножением и делением десятичных дробей.

Деление и умножение десятичных дробей.jpg
Пройди тестирование
Пройди тестирование
Источник — «https://bb.edu.gov.kg/index.php?title=Математика:_Арифметические_действия_над_десятичными_дробями&oldid=27422»