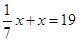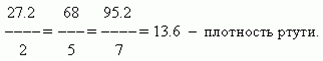БИЛИМ БУЛАГЫ

Математика: Решение уравнений — различия между версиями

Строка 3: Строка 3:
 
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content -->  
 
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content -->  
 
{{Якорь|Начало}}
 
{{Якорь|Начало}}
−
<div class="cutok">[[#Натуральные числа|Натуральные числа]] [[#Системы измерения и счет у древних кыргызов|Системы измерения и счет у древних кыргызов]]</div>
 
  
−
<div class="show-for-large-up">{{center|[[Файл:Анимашка натуральные числа.gif|400px]]}}</div>
 
−
<div class="hide-for-large-up">{{center|[[Файл:Анимашка натуральные числа.gif|400px]]}}</div>
 
  
−
<br>
+
Еще в глубокой древности в математических сочинениях встречались уравнения, а также задачи, решаемые с помощью уравнений. Так, в египетском папирусе около 2000 лет до нашей эры (причем, как указывает в нем автор, писец Ахмес, это математическое сочинение является копией с другого, более древнего сочинения) имелись задачи на отыскание неизвестного числа. Это неизвестное называлось «хау» (куча) и обозначалось особым иероглифом.
−
Мы умеем  выражать  свои чувства, эмоции и отношение к чему-то или к кому-то с помощью слов. В разговоре, обращаясь друг с другом, мы используем слова. В математике также существует свой язык, и выражается он не только словами, но и числами. У древних людей кроме топора, сделанного из камня, и одежды из шкуры ничего не было, поэтому считать им было нечего. Со временем они стали приручать животных, обрабатывать поля, и появилась торговля. Тут уж без счёта им стало не обойтись. Сначала считали на пальцах. Когда пальцев одной руки не хватало, переходили на пальцы второй руки, а если считать нужно было дальше и пальцев обеих рук не хватало, то переходили на пальцы ног. Расширяющиеся потребности счёта заставили людей употреблять другие счётные эталоны. Так, например, для записи сравнительно большего число стала использоваться новая идея - обозначение новым знаком - зарубкой на другой палочке. С развитием письменности возможности воспроизведения числа значительно расширились. Сначала числа стали обозначаться чёрточками на материале, служащем для записи (папирус, глиняные таблички и т.д.). Затем были введены другие знаки для больших чисел. Таким образом, параллельно с развитием письменности понятие натурального числа закрепляется в устной речи и в форме обозначения специальными знаками (в письменности).
 
−
==Натуральные числа==
 
−
Чисел очень много, поэтому математики разбили их на несколько групп. Самая маленькая из них – натуральные числа. С их помощью мы можем говорить о количестве предметов, а также можем назвать порядковый номер во множестве предметов. Например, мы можем сосчитать, сколько  деревьев  растет возле дома. А если вспомнить урок физкультуры, когда учитель просит вас рассчитаться в строю, то, наверняка, каждый из вас может без особого труда назвать свой номер.
 
  
−
Итак, числа, которыми мы с вами пользовались при счёте, называют натуральными числами. Обозначают их латинской буквой N.  
+
Вот примеры задач из этого папируса.
  
−
Натуральные числа также употребляют, чтобы выразить результаты измерения различных величин: длины, площади, времени, скорости. Кроме натуральных чисел мы знаем ещё число 0 (нуль). При счёте число нуль не используется, а означает оно «ни одного». Поэтому число 0 (нуль) не является натуральным!
+
1) «Неизвестное, его седьмая часть, его целое составляет 19».
  
−
<div class="show-for-large-up">{{center|[[Файл:Ряд натуральных чисел.mp4|400px]]}}</div>
+
В современном виде задача запишется так:   
−
<div class="hide-for-large-up">{{center|[[Файл:Ряд натуральных чисел.mp4|400px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:1_7.png|100px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:1_7.png|100px]]}}</div>
  
−
==Системы измерения и счет у древних кыргызов==
+
2) «[[Файл:2_3.png|100px]] сложено и [[Файл:1_3.png|100px]]  отнята: остаток 10».
 +
В папирусе решению, задачу следует понимать так: к неизвестному прибавлено [[Файл:2_3.png|100px]]  его и отнята [[Файл:1_3.png|100px]] полученной суммы; остаток 10; найти число.
 +
Задача в современном виде запишется так: [[Файл:X_2.png|100px]] ; Ответ:  х=9
  
−
Потребность в измерении и счете родилась у кыргызов в условиях относительно высокоразвитого их общественного производства и социальной дифференциации общества. В кыргызском народе до сих пор своеобразно уживаются несколько систем счета, что свидетельствует о различных их источниках.  
+
3) У Диофанта также встречаются уравнения с одним неизвестным, например:
 +
«Числа 20 и 100. Нужно одно и то же число прибавить к меньшему и вычесть из большего; отношение суммы к разности равно 4».
 +
Задача приводит к уравнению: [[Файл:20+x.png|100px]]
  
−
Древние кыргызы употребляли известные цивилизованному миру действительные математические числа и могли сосчитать членов своей семьи, домашних животных, стрелы в колчане лука, убитых или пойманных на охоте зверей, птиц.
+
4) В индийской рукописной арифметике VII и VIII века нашей эры, являющейся копией с более древней рукописи (III-IV века), имеется такая задача:
 +
«Из четырех жертвователей второй дал вдвое больше первого, третий втрое больше второго, четвертый вчетверо больше третьего, а все вместе дали 132.
 +
Сколько дал первый?»
 +
Получаем уравнение: 
 +
В рукописи задача решается способом «ложного положения». (Этим способом пользовался и Л.Ф. Магницкий в своей «Арифметике».)
 +
«Если бы первый дал 1, то второй бы 2, третий 6, четвертый 24, а все вместе 33. Но всего было 132, то есть вчетверо больше. Значит, и каждый из жертвователей дал вчетверо больше».
 +
Ответ: 4; 8; 24; 96.
  
−
<div class="show-for-large-up">{{center|[[Файл:Натуральные числа др кырг.gif|600px]]}}</div>
+
Но общее правило для решения уравнений первой степени с одним неизвестным дал в IX веке Мухаммед аль-Хорезми.
−
<div class="hide-for-large-up">{{center|[[Файл:Натуральные числа др кырг.gif|600px]]}}</div>
+
В своем сочинении «'''Аль-джебр и аль-мукабала'''» он дает два приема, применяемых при решении уравнений.
  
−
В быту с помощью понятия  «бирдин учу» говорили о  небольшом количестве предметов. Например, два — три, три — четыре, пять — шесть). Анин чакан уйунун торундо бирдин учу болуп олтурушкан кишилер — В его маленькой юрте на почетном месте сидели несколько (немного) человек или Бирдин учу эле малы бар — У него немного скота (три — четыре, пять — шесть голов).
+
1) ''Прием «аль-джебр» заключается в том, что если имеются в уравнении отрицательные (вычитаемые) члены, то следует прибавить противоположные им члены к обеим частям уравнения, и тогда все члены будут положительными.
  
−
В эпосе «Жаныл Мырза» встречается старинное кыргызское слово, передающее математическое понятие количества, употребляемое при счете животных — санга.
+
2) Прием «аль-мукабала» заключается в вычитании из обеих частей уравнения одинаковых членов, что приводит к его упрощению.''
  
−
''Эки санга толуптур''
+
Например, дано уравнение:  5х-17=2х-5
 +
Применим «'''аль-джебр'''»: прибавляем к каждой части уравнения 5 и 17.
 +
Получим:  5х+5=2х+17
 +
Применим «'''аль-мукабала'''»: вычитаем из каждой части 2x и 5. Получим:  3х=12
 +
Отсюда легко находится х.
 +
Появление этого замечательного сочинения аль-Хорезми можно считать началом выделения алгебры как самостоятельной, отдельной отрасли математики.
 +
Самое название «алгебра» взято из заглавия этого сочинения («Аль-джебр»).
  
−
''Эсепсиз жылкы болуптур .''
+
'''Основное свойство пропорции:'''  ''Произведение крайних членов пропорции равно произведению её средних членов.''  
  
−
''При подсчете коней''
+
''Две взаимно зависимых величины называются пропорциональными, если отношение их величин сохраняется неизменным. Это постоянное отношение пропорциональных величин называется коэффициентом пропорциональности.''
  
−
''Количество их равнялось двум санга.''
+
П р и м е р . Масса любого вещества пропорциональна его объёму. Например, 2 литра ртути весят 27.2 кг, 5 литров весят 68 кг, 7 литров весят 95.2 кг. Отношение массы ртути к её объёму ( коэффициент пропорциональности ) будет равно:
  
−
Поскольку данное понятие не выражало вполне конкретное, определенное количество, его использование было связано с разными трудностями, осложняло это и одновременное употребление различных систем счета. Наряду с десятичным широко было распространено двенадцатиричное (по дюжинам) исчисление, применительно к различным классам объектов, в частности, оно применялось в измерении, в основу которого было положено сравнение с известными объектами — частями тела, предметами обихода. Практическое удобство применения последнего вида измерения несомненно, однако оно было весьма приблизительным.
+
<div class="show-for-large-up">{{center|[[Файл:Плотность_ртути.png|600px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Плотность_ртути.png|600px]]}}</div>
 +
       
 +
Таким образом, коэффициентом пропорциональности в данном примере является плотность.
  
−
==Полезные ссылки==
+
''Пропорциональность''. Это простейший вид функциональной зависимости. Различают прямую пропорциональность. (y = kx) и обратную пропорциональность ( y= k/ x). Напр., путь S, пройденный при равномерном движении со скоростью  v, пропорционален времени  t, т. е.  S = vt ; прямо пропорциональна величина основания  y прямоугольника с заданной площадью a обратно пропорциональна высоте x, т. е. y = a/ x.
−
«Я не знаю ничего более прекрасного в арифметике, чем эти числа, называемые некоторыми планетарными, а другими – магическими», - писал о числах известный французский математик, один из создателей теории чисел Пьер де Ферма. Привлекающие естественной красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множества тайн. В своей жизни каждый из нас сталкивается с числами. Курс школьной программы, да и дальнейшую жизнь, трудно представить без них.  Более подробно читаем в исследовательская работе "Магические числа" http://collegy.ucoz.ru/publ/89-1-0-3365
 
  
−
==Глоссарий==
+
'''Свойства прямой пропорциональной зависимости.'''  
−
'''Число́''' — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.
 
  
−
== Библиография ==
+
1. Каждому значению х соответствует единственное определенное значение у. (''первое свойство прямой пропорциональной зависимости'').
−
*Видеоурок по математике «Ряд натуральных чисел»: [Электронный ресурс] //ООО «Мультиурок», 2008-2017. URL: https://videouroki.net/blog/vidieourok-po-matiematikie-riad-natural-nykh-chisiel.html. (дата обращения: 20.11.2017)
 
−
*Энциклопедический словарь юного математика.  2-е изд., испр. и доп. - М.: Педагогика, 1989 - 352 с
 
−
*Системы измерения и счет у кыргызов.: [Электронный ресурс] //Open.kg Открытый Кыргызстан. URL:  https://www.open.kg/about-kyrgyzstan/culture/ethnography/1970-sistemy-izmereniya-i-schet-u-kyrgyzov.html. (дата обращения: 20.11.2017)
 
−
*Интересные факты о цифрах и числах.: [Электронный ресурс] // Знаменитости 2014. URL: http://kvipstar.com/blog/facts/341.html. (дата обращения: 20.11.2017)
 
−
*Видео «5 простых математических фокусов»: [Электронный ресурс] // Простая математика YouTube, 2017. https://www.youtube.com/watch?v=JlgsMsnZmz8. (дата обращения: 20.11.2017)
 
−
*Учительские университеты. Исследовательская работа "Магические числа". Ростовская средняя школа
 
−
*Научное общество учащихся: [Электронный ресурс] // Педагогический журнал "Коллеги" Интернет-портал "Детство-kz", 2017  http://collegy.ucoz.ru/publ/89-1-0-3365. (дата обращения: 20.11.2017)
 
  
−
<div class="light" style="float:right;>[[#Начало|В начало]]</div>
+
2. Отношение соответствующих значений величин у и х, связанных прямой пропорциональностью, равно коэффициенту пропорциональности.
  
−
</div>
+
3. Если две величины связаны между собой прямой пропорциональной зависимостью, то при увеличении (уменьшении) одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз.
  
−
<!-- Sidebar -->
+
<div class="show-for-large-up">{{center|[[Файл:Математическая_модель.png|600px]]}}</div>
−
<div class="large-4 medium-5 columns">
+
<div class="hide-for-large-up">{{center|[[Файл:Математическая_модель.png|600px]]}}</div>  
−
<!-- Первый элемент сайдбара Это интересно или топ5/10/15 -->
 
−
<div class="shadow radius sbstyle">
 
−
<div class="row">
 
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Это Интересно</div>
 
−
</div>
 
−
<span class="firstcharacter">'''С'''</span><p align="justify">амые интересные факты о числах, которые не оставят вас равнодушными
 
−
1. Несчастливые числа. В таких странах, как Китай, Япония и Корея число «4»  считается несчастливым. Поэтому этажи с номерами, которые заканчиваются на «4» отсутствуют.
 
−
*Число «13» - во многих государствах также считается неудачным. Поэтому этаж после «12»  имеет обозначение «14», «12А» или «М» (тринадцатая буква в алфавите).
 
−
*А в Греции «13»  считается несчастливым днем только тогда, когда выпадает во вторник. В Италии опасаются пятницы 17-го. А вот статисты Нидерландов подсчитали, что именно 13-го числа случается меньше аварий и несчастных случаев, поскольку люди более осторожны и собраны.
 
  
−
<div class="show-for-large-up">{{center|[[Файл:Несчастливые числа интересно о числах.jpg|450px]]}}</div>
+
'''Свойства обратной пропорциональной зависимости.'''
−
<div class="hide-for-large-up">{{center|[[Файл:Несчастливые числа интересно о числах.jpg|450px]]}}</div>
 
  
 +
1. Каждому значению х (за исключением х=0) соответствует вполне определенное значение у.
  
−
2. Числа великаны. Один из первых, кто научился называть большие числа, был древнегреческий математик Архимед. Названия были, но обозначать он их не мог. Архимед, один из гениальнейших математиков, не додумался до нуля. Впервые нуль был придуман вавилонянами примерно 2 тысячи лет назад. Однако, открытие писать нули в конце числа, было сделано в Индии полторы тысячи лет назад. Нуль был присоединен к девяти цифрам, и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно ни было. Числа-великаны имеют свои названия:
+
2. Произведение соответствующих значений х и у равно коэффициенту обратной пропорциональности.
  
−
1000 единиц – просто тысяча
+
3. Если х увеличивается (уменьшается) в несколько раз, то у уменьшается (увеличивается) во столько же раз, так как их произведение остается неизменным.
  
−
1000 тысяч – 1 миллион
+
<div class="show-for-large-up">{{center|[[Файл:Обратная_пропорциональность.png|600px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Обратная_пропорциональность.png|600px]]}}</div>
  
−
1000 миллионов – 1 биллион (или миллиард)
+
Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.
  
−
1000 биллионов – 1 триллион
+
<div class="show-for-large-up">{{center|[[Файл:Золотое_сечение.png|600px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Золотое_сечение.png|600px]]}}</div>
  
−
1000 триллионов – 1 квадриллион
+
Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длинна всего отрезка так относится к длине его большей части, как длинна большей части к меньшей. Приближенно это отношение равно 0, 618  ≈5/8. Золотое сечение чаще всего применяется в произведениях искусства, архитектуре, встречается и в природе.
 +
 +
Применение «золотого сечения». 
  
−
1000 квадриллионов - 1 квинтиллион
+
У древних основу составляла теория пропорций. Отношение размеров частей человеческого тела связывалось с формулой «золотого сечения». Скульпторы утверждают, что талия делит человеческое тело (образцом которого является Апполон Бельведерский) в отношении «золотого сечения». а:х=1,618. 
  
−
1000 квинтиллионов – 1 секстиллион
+
Окружающие предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длинны, близкое к 0,618.
  
−
1000 секстиллионов – 1 септиллион
+
<div class="show-for-large-up">{{right|[[Файл:Лист_дерева.png|600px]]}}</div>
 +
<div class="hide-for-large-up">{{right|[[Файл:Лист_дерева.png|600px]]}}</div>
  
−
1000 септиллионов – 1октиллион
+
Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В).
  
−
1000 октиллионов – 1 нониллион
 
  
−
Гугол - число содержащее единицу и сто нулей.
+
==Полезные ссылки==
 +
В математике отношением называется то частное, которое получается при делении одного числа на другое. Ранее сам этот термин использовался только в тех случаях, когда было необходимо выражение какой-либо одной величины в долях другой, причем такой, которая однородна первой. К примеру, отношения использовались при выражении площади в долях другой площади, длины в долях другой длины и т.п. Решение этой задачи производилось с помощью деления. http://simple-math.ru/arithmetics/ratio-proportion.php
  
−
Гуголплекс — число, изображаемое единицей с гуголом нулей.
 
  
−
Числа гугол, гуголплекс были придуманы американским математиком Эдвардом Каснером  и его племянником Милтоном Сиротта.
+
==Глоссарий==
 +
'''Уравнение''' - это некоторые выражения, между которыми стоит обязательно знак равенства. В этих выражениях присутствуют буквы, так называемые переменные, значение которых и необходимо найти.
 +
'''Переменные''' - атрибут системы, который меняет свое значение. Они обозначаются буквами, например, х, а, b, с...  
  
−
<div class="show-for-large-up">{{center|[[Файл:Числа великаны интересно о числах.jpg|450px]]}}</div>
+
== Библиография ==
−
<div class="hide-for-large-up">{{center|[[Файл:Числа великаны интересно о числах.jpg|450px]]}}</div>
+
*Видеоурок на тему «Прямая и обратная пропорциональные зависимости» http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html
 +
*Видеоурок на тему «Пропорции» http://znaika.ru/catalog/6-klass/matematika/Proportsii.html
  
  
−
3. Терминология.  Термин «цифра» в переводе с арабского означает «ноль». Только со временем данное слово начали использовать для обозначения любого численного символа.
+
<div class="light" style="float:right;>[[#Начало|В начало]]</div>
  
−
Важно помнить, что цифры —  это система знаков для записи конкретных значений чисел. Все числа состоят из цифр. Цифры и числа различных систем счисления настолько не совпадают, что число одной системы может оказаться цифрой другой, а всё потому, что это отвлечённые, выдуманные человеком понятия.
+
</div>
  
−
<div class="show-for-large-up">{{center|[[Файл:Исправлен Терминология интересно о числах.jpg|450px]]}}</div>
+
<!-- Sidebar -->
−
<div class="hide-for-large-up">{{center|[[Файл:Исправлен Терминология интересно о числах.jpg|450px]]}}</div>
+
<div class="large-4 medium-5 columns">
 +
<!-- Первый элемент сайдбара Это интересно или топ5/10/15 -->
 +
<div class="shadow radius sbstyle">
 +
<div class="row">
 +
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Это Интересно</div>
 +
</div>
 +
<span class="firstcharacter">'''П'''</span><p align="justify">ропорция применяется везде!
 +
 
 +
<div class="show-for-large-up">{{right|[[Файл:Пропорция.png|600px]]}}</div>
 +
<div class="hide-for-large-up">{{right|[[Файл:Пропорция.png|600px]]}}</div>  
 +
 
 +
Например:
  
 +
'''1. Пропорция в физике.'''
  
−
</p>
+
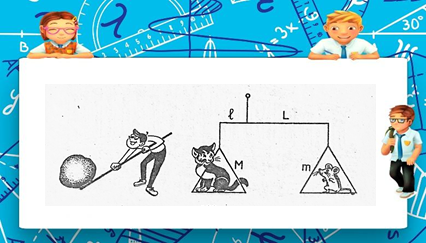
С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т.д. – примеры рычагов. Выигрыш, который дает рычаг в прилагаемом усилии, определяется пропорцией, где M и m – массы грузов, а L и l – «плечи» рычага.
−
</div>
+
 
−
<!-- четвертый элемент сайдбара математический диктант -->
+
<div class="show-for-large-up">{{right|[[Файл:Кошка.png|600px]]}}</div>
−
<div class="shadow radius sbstyle" style="margin-top:20px;">
+
<div class="hide-for-large-up">{{right|[[Файл:Кошка.png|600px]]}}</div>  
−
<div class="row">
+
 
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Математический диктант «Чтение натуральных чисел»</div>
+
'''2. Пропорция в географии.'''
−
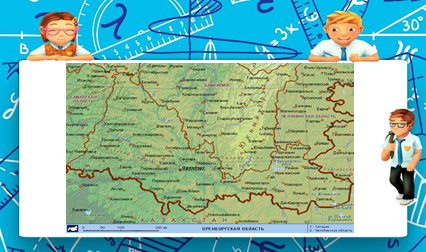
</div>
+
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
 +
 
 +
<div class="show-for-large-up">{{right|[[Файл:Пропорция_география.png|600px]]}}</div>
 +
<div class="hide-for-large-up">{{right|[[Файл:Пропорция_география.png|600px]]}}</div>  
  
−
Давайте проверим, умеете ли вы правильно читать и записывать натуральные числа. В конце диктанта вас ждет приятный сюрприз.
+
'''3. Пропорция в музыке.'''
−
<div class="show-for-large-up">{{center|[[Файл:Математический диктант чтение нат чисел.mp4|450px]]}}</div>
+
Музыкой греки называли ту часть арифметики, в которой говорится об отношениях и пропорциях. Греки создали и научную теорию. Музыки. Они знали: чем «длиннее» натянутая струна, тем «ниже» получается звук, который она издает; что короткая струна издает высокий звук. Однако у музыкального инструмента не одна, а несколько струн, и для того, чтобы все струны при игре звучали «согласно», приятно для уха, длина звучащих частей их должна быть в определенном отношении. Например, чтобы высоты звуков, издаваемых двумя струнами, различались на октаву, нужно, чтобы их длины относились как 1:2. Подобным образом квинте соответствует отношение 2:3, кварте-отношение 3:4 и т.д.
−
<div class="hide-for-large-up">{{center|[[Файл:Математический диктант чтение нат чисел.mp4|450px]]}}</div>
 
  
−
</div>
+
<div class="show-for-large-up">{{right|[[Файл:Пропорция_музыка.png|600px]]}}</div>
 +
<div class="hide-for-large-up">{{right|[[Файл:Пропорция_музыка.png|600px]]}}</div>  
  
−
<!-- четвертый элемент сайдбара лайфхак -->
+
'''4. Пропорции в архитектуре'''
−
<div class="shadow radius sbstyle" style="margin-top:20px;">
+
Пропорции в архитектуре – это ее внутренняя красота.
−
<div class="row">
+
ПАРФЕНОН, храм Афины Парфенос на Акрополе в Афинах, памятник древнегреческой высокой классики. Мраморный дорический периптер с ионическим скульптурным фризом (447-438 до н. э., архитекторы Иктин и Калликрат) замечателен величественной красотой форм и пропорций. Статуи фронтонов, рельефы метоп и фриза (окончены в 432 до н. э.) созданы под руководством Фидия. Разрушен в 1687; частично восстановлен. Отношение высоты здания к его длине равно 0, 618.
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Лайфхак</div>
 
−
</div>
 
  
−
Вы уже знаете, что для записи чисел используют цифры, и когда число состоит из одной цифры, мы называем его однозначным, из двух – двузначным. Такие числа с легкостью читаем. А что делать, когда в записи больше трех цифр? Смотри лайфхак и запоминай!
+
<div class="show-for-large-up">{{right|[[Файл:Пропорция_архитектура.png|600px]]}}</div>
 +
<div class="hide-for-large-up">{{right|[[Файл:Пропорция_архитектура.png|600px]]}}</div>
  
−
<div class="show-for-large-up">{{center|[[Файл:Чтение натуральных чисел.gif|450px]]}}</div>
+
'''5. Пропорции в скульптуре.'''
−
<div class="hide-for-large-up">{{center|[[Файл:Чтение натуральных чисел.gif|450px]]}}</div>
+
АПОЛЛОН БЕЛЬВЕДЕРСКИЙ, статуя Аполлона — мраморная римская копия бронзового оригинала работы древнегреческого скульптора Леохара  (ок. 330-320 до н. э., Музей Пио-Клементино, Ватикан). Название от ватиканского дворца Бельведер, где выставлена статуя. Долгое время считалась вершиной греческого искусства. На рисунке представлена статуя Аполлона Бельведерского, разделенная в отношении (точка С делит отрезок АD, точка В делит отрезок АС)
  
−
</div>
+
<div class="show-for-large-up">{{right|[[Файл:Пропорция_скульптура.png|600px]]}}</div>
 +
<div class="hide-for-large-up">{{right|[[Файл:Пропорция_скульптура.png|600px]]}}</div>  
  
  
Строка 149: Строка 167:
 
<div class="shadow radius sbstyle" style="margin-top:20px;">
 
<div class="shadow radius sbstyle" style="margin-top:20px;">
 
<div class="row">
 
<div class="row">
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Математические фокусы</div>
+
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Лайфхак</div>
 
</div>
 
</div>
−
Математические фокусы — самые простые в исполнении. Для них не нужен реквизит, длительная подготовка и специальное место для демонстрации. Смысл таких фокусов — в отгадывании чисел, задуманных зрителями, или в каких-нибудь операциях над ними. Все чудеса основаны на математических закономерностях, такие фокусы можно проделывать на уроках математики. Смотрим и учимся математической магии.
 
  
−
<div class="show-for-large-up">{{center|[[Файл:5_математических__фокусов.mp4|450px]]}}</div>
+
Есть у пропорции правило главное<br />
−
<div class="hide-for-large-up">{{center|[[Файл:5_математических__фокусов.mp4|450px]]}}</div>
+
 
 +
Все его знать и запомнить должны<br />
 +
 
 +
Средние члены умножишь и крайние<br />
  
 +
Будут всегда эти числа равны.
  
 
</div>
 
</div>
  
 
</div>
 
</div>
−
½⅓
 

Версия 12:31, 16 января 2018


Еще в глубокой древности в математических сочинениях встречались уравнения, а также задачи, решаемые с помощью уравнений. Так, в египетском папирусе около 2000 лет до нашей эры (причем, как указывает в нем автор, писец Ахмес, это математическое сочинение является копией с другого, более древнего сочинения) имелись задачи на отыскание неизвестного числа. Это неизвестное называлось «хау» (куча) и обозначалось особым иероглифом.

Вот примеры задач из этого папируса.

1) «Неизвестное, его седьмая часть, его целое составляет 19».

В современном виде задача запишется так:

1 7.png
1 7.png

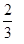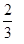2) «2 3.png сложено и 1 3.png отнята: остаток 10». В папирусе решению, задачу следует понимать так: к неизвестному прибавлено 2 3.png его и отнята 1 3.png полученной суммы; остаток 10; найти число. Задача в современном виде запишется так: X 2.png ; Ответ: х=9

3) У Диофанта также встречаются уравнения с одним неизвестным, например: «Числа 20 и 100. Нужно одно и то же число прибавить к меньшему и вычесть из большего; отношение суммы к разности равно 4». Задача приводит к уравнению: 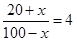20+x.png

4) В индийской рукописной арифметике VII и VIII века нашей эры, являющейся копией с более древней рукописи (III-IV века), имеется такая задача: «Из четырех жертвователей второй дал вдвое больше первого, третий втрое больше второго, четвертый вчетверо больше третьего, а все вместе дали 132. Сколько дал первый?» Получаем уравнение: В рукописи задача решается способом «ложного положения». (Этим способом пользовался и Л.Ф. Магницкий в своей «Арифметике».) «Если бы первый дал 1, то второй бы 2, третий 6, четвертый 24, а все вместе 33. Но всего было 132, то есть вчетверо больше. Значит, и каждый из жертвователей дал вчетверо больше». Ответ: 4; 8; 24; 96.

Но общее правило для решения уравнений первой степени с одним неизвестным дал в IX веке Мухаммед аль-Хорезми. В своем сочинении «Аль-джебр и аль-мукабала» он дает два приема, применяемых при решении уравнений.

1) Прием «аль-джебр» заключается в том, что если имеются в уравнении отрицательные (вычитаемые) члены, то следует прибавить противоположные им члены к обеим частям уравнения, и тогда все члены будут положительными.

2) Прием «аль-мукабала» заключается в вычитании из обеих частей уравнения одинаковых членов, что приводит к его упрощению.

Например, дано уравнение: 5х-17=2х-5 Применим «аль-джебр»: прибавляем к каждой части уравнения 5 и 17. Получим: 5х+5=2х+17 Применим «аль-мукабала»: вычитаем из каждой части 2x и 5. Получим: 3х=12 Отсюда легко находится х. Появление этого замечательного сочинения аль-Хорезми можно считать началом выделения алгебры как самостоятельной, отдельной отрасли математики. Самое название «алгебра» взято из заглавия этого сочинения («Аль-джебр»).

Основное свойство пропорции: Произведение крайних членов пропорции равно произведению её средних членов.

Две взаимно зависимых величины называются пропорциональными, если отношение их величин сохраняется неизменным. Это постоянное отношение пропорциональных величин называется коэффициентом пропорциональности.

П р и м е р . Масса любого вещества пропорциональна его объёму. Например, 2 литра ртути весят 27.2 кг, 5 литров весят 68 кг, 7 литров весят 95.2 кг. Отношение массы ртути к её объёму ( коэффициент пропорциональности ) будет равно:

Плотность ртути.png
Плотность ртути.png

Таким образом, коэффициентом пропорциональности в данном примере является плотность.

Пропорциональность. Это простейший вид функциональной зависимости. Различают прямую пропорциональность. (y = kx) и обратную пропорциональность ( y= k/ x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S = vt ; прямо пропорциональна величина основания y прямоугольника с заданной площадью a обратно пропорциональна высоте x, т. е. y = a/ x.

Свойства прямой пропорциональной зависимости.

1. Каждому значению х соответствует единственное определенное значение у. (первое свойство прямой пропорциональной зависимости).

2. Отношение соответствующих значений величин у и х, связанных прямой пропорциональностью, равно коэффициенту пропорциональности.

3. Если две величины связаны между собой прямой пропорциональной зависимостью, то при увеличении (уменьшении) одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз.

Математическая модель.png
Математическая модель.png

Свойства обратной пропорциональной зависимости.

1. Каждому значению х (за исключением х=0) соответствует вполне определенное значение у.

2. Произведение соответствующих значений х и у равно коэффициенту обратной пропорциональности.

3. Если х увеличивается (уменьшается) в несколько раз, то у уменьшается (увеличивается) во столько же раз, так как их произведение остается неизменным.

Обратная пропорциональность.png
Обратная пропорциональность.png

Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.

Золотое сечение.png
Золотое сечение.png

Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длинна всего отрезка так относится к длине его большей части, как длинна большей части к меньшей. Приближенно это отношение равно 0, 618 ≈5/8. Золотое сечение чаще всего применяется в произведениях искусства, архитектуре, встречается и в природе.

Применение «золотого сечения».

У древних основу составляла теория пропорций. Отношение размеров частей человеческого тела связывалось с формулой «золотого сечения». Скульпторы утверждают, что талия делит человеческое тело (образцом которого является Апполон Бельведерский) в отношении «золотого сечения». а:х=1,618.

Окружающие предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длинны, близкое к 0,618.

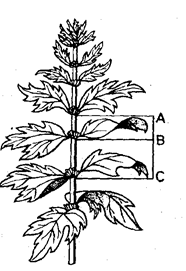
Лист дерева.png
Лист дерева.png

Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В).


Полезные ссылки

В математике отношением называется то частное, которое получается при делении одного числа на другое. Ранее сам этот термин использовался только в тех случаях, когда было необходимо выражение какой-либо одной величины в долях другой, причем такой, которая однородна первой. К примеру, отношения использовались при выражении площади в долях другой площади, длины в долях другой длины и т.п. Решение этой задачи производилось с помощью деления. http://simple-math.ru/arithmetics/ratio-proportion.php


Глоссарий

Уравнение - это некоторые выражения, между которыми стоит обязательно знак равенства. В этих выражениях присутствуют буквы, так называемые переменные, значение которых и необходимо найти. Переменные - атрибут системы, который меняет свое значение. Они обозначаются буквами, например, х, а, b, с...

Библиография


В начало
Это Интересно
П

ропорция применяется везде!

Пропорция.png
Пропорция.png

Например:

1. Пропорция в физике.

С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т.д. – примеры рычагов. Выигрыш, который дает рычаг в прилагаемом усилии, определяется пропорцией, где M и m – массы грузов, а L и l – «плечи» рычага.

Кошка.png
Кошка.png

2. Пропорция в географии. Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.

Пропорция география.png
Пропорция география.png

3. Пропорция в музыке. Музыкой греки называли ту часть арифметики, в которой говорится об отношениях и пропорциях. Греки создали и научную теорию. Музыки. Они знали: чем «длиннее» натянутая струна, тем «ниже» получается звук, который она издает; что короткая струна издает высокий звук. Однако у музыкального инструмента не одна, а несколько струн, и для того, чтобы все струны при игре звучали «согласно», приятно для уха, длина звучащих частей их должна быть в определенном отношении. Например, чтобы высоты звуков, издаваемых двумя струнами, различались на октаву, нужно, чтобы их длины относились как 1:2. Подобным образом квинте соответствует отношение 2:3, кварте-отношение 3:4 и т.д.

Пропорция музыка.png
Пропорция музыка.png

4. Пропорции в архитектуре Пропорции в архитектуре – это ее внутренняя красота. ПАРФЕНОН, храм Афины Парфенос на Акрополе в Афинах, памятник древнегреческой высокой классики. Мраморный дорический периптер с ионическим скульптурным фризом (447-438 до н. э., архитекторы Иктин и Калликрат) замечателен величественной красотой форм и пропорций. Статуи фронтонов, рельефы метоп и фриза (окончены в 432 до н. э.) созданы под руководством Фидия. Разрушен в 1687; частично восстановлен. Отношение высоты здания к его длине равно 0, 618.

Пропорция архитектура.png
Пропорция архитектура.png

5. Пропорции в скульптуре. АПОЛЛОН БЕЛЬВЕДЕРСКИЙ, статуя Аполлона — мраморная римская копия бронзового оригинала работы древнегреческого скульптора Леохара (ок. 330-320 до н. э., Музей Пио-Клементино, Ватикан). Название от ватиканского дворца Бельведер, где выставлена статуя. Долгое время считалась вершиной греческого искусства. На рисунке представлена статуя Аполлона Бельведерского, разделенная в отношении (точка С делит отрезок АD, точка В делит отрезок АС)

Пропорция скульптура.png
Пропорция скульптура.png


Лайфхак

Есть у пропорции правило главное

Все его знать и запомнить должны

Средние члены умножишь и крайние

Будут всегда эти числа равны.

</div>

Источник — «https://bb.edu.gov.kg/index.php?title=Математика:_Решение_уравнений&oldid=8748»