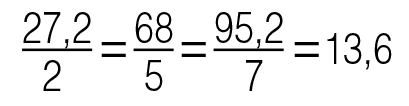БИЛИМ БУЛАГЫ

Математика: Отношения и пропорции — различия между версиями

(→‎Библиография)
 
(не показано 67 промежуточных версий 2 участников)
Строка 1: Строка 1:
−
__NOTOC__
 
 
<div class="row mat-bg">
 
<div class="row mat-bg">
 
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content -->  
 
<div class="maintext math-back math-bg large-8 medium-7 columns"> <!-- Page Content -->  
 
{{Якорь|Начало}}
 
{{Якорь|Начало}}
  
−
Впервые интерес к пропорции, возникающей при делении отрезка в крайнем и среднем отношении, возникает в античной науке (Пифагор, Платон, Евклид). Удивительные математические свойства этой пропорции уже тогда создают вокруг нее ореол таинственности и мистического поклонения. Слово «пропорция» ввел в употребление Цицерон в 1 веке до н.э., который буквально означал аналогия, соотношение.
+
==История развития учения о пропорции==
  
−
Слово «пропорция» (от латинского propotio) означает «соразмерность», «определённое соотношение частей между собой».  В математике: равенство двух отношений. Учение об отношениях и пропорциях особенно успешно развивалось в IV веке до нашей эры в Древней Греции, славившейся произведениями искусства, архитектуры, различными ремеслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Принято считать, что понятие о золотом деление ввел в научный обиход Пифагор, древнегреческий философ и математик. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды, храмов, барельефов, предметов быта и украшений гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создания. Термин золотое сечение ввел Леонардо да Винчи (1452-1519 гг)
+
          '''Ничто не нравится, кроме красоты, в красоте – ничто, кроме форм, в формах – ничто,'''
 +
              '''кроме пропорций, в пропорциях – ничто, кроме числа.'''
 +
                                                            '''Аврелий Августин'''
  
−
Теория отношений и пропорций была подробно изложена в «Началах» Евклида (III век до нашей эры). Оно звучит так: '''«В верной пропорции произведение крайних членов равно произведению средних».''' 
+
<div class="textblock">{{center|Понятие пропорции как равенства двух отношений чисел для целых чисел было дано в глубокой древности. Еще древние вавилоняне пришли к понятию пропорциональности сторон  подобных треугольников, выраженных в целых числах.}}</div>
  
−
Благодаря пропорции, по словам Альберти, « тихим и вольным течением взор, точно скользя по карнизам, по простенкам и по всей наружной и внутренней сторонам здания, будет умножать наслаждение новым наслаждением от сходства и несходства».
+
Впервые интерес к пропорции, образующейся при делении отрезка в крайнем и среднем отношении, возникает в античной науке.
−
 
 
−
Например, 12 : 20 = 3 : 5;      a : b = c : d .
 
−
 
−
Крайние члены пропорции: 12 и 5 в первой пропорции;  a и  d – во второй.
 
  
−
Средние члены пропорции: 20 и 3 в первой пропорции; b и  с – во второй.
+
Так в  Древней Греции, славившейся произведениями искусства, архитектуры, различными ремеслами, успешно развивалось  учение об отношениях и пропорциях. С ними связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Принято считать, что понятие о делении отрезка ввел в научный обиход Пифагор, древнегреческий философ и математик. Он и его ученики рассматривали три вида пропорций:
  
 +
* '''Арифметическую: а - b = с - d'''
  
−
<div class="show-for-large-up">{{center|[[Файл:P1.png|600px]]}}</div>
+
* '''Геометрическую: a : b = c : d'''
−
<div class="hide-for-large-up">{{center|[[Файл:P1.png|600px]]}}</div>
 
  
−
'''Основное свойство пропорции:'''  
+
* '''Гармоническую: a : b = b : (a - b)'''
−
 
−
Произведение крайних членов пропорции равно произведению её средних членов. 
 
  
−
Две взаимно зависимых величины называются пропорциональными, если отношение их величин сохраняется неизменным. Это постоянное отношение пропорциональных величин называется коэффициентом пропорциональности.
+
Другой древнегреческий ученый  Платон  сводил сущность пропорции к тому, что «для соединения двух частей с третьей совершенным образом необходима пропорция, которая бы «скрепила» их в единое целое. При этом одна часть целого должна так относиться к другой, как целое к большей части. Такая пропорция отвечает гармоническому соединению, она и является золотой».
 +
 
 +
А древнегреческий ученый Евдокс  дал систематическое учение о пропорциях применительно не только к целым, но и к дробным числам. Строгая теория пропорций была построена в 3 веке до н.э. древнегреческим геометром Евклидом в его знаменитых «Началах», состоящих из 13 книг. Этой теории он посвящает 5 книг. В основу своей теории Евклид положил учение Евдокса. В настоящее время теория пропорций мало отличается от теории Евдокса – Евклида.  Евклид  определяет сравнение между пропорциями: отношение a : b меньше, чем отношение c : d, если есть такие числа m и n, если ma > nb и в то же время mc ≤ nd.  А читается она  так: «В верной пропорции произведение крайних членов равно произведению средних». 
 +
Математические свойства  пропорции уже тогда создавали вокруг нее ореол таинственности и мистического поклонения. Удивителен тот факт, что  слово «пропорция» ввел в употребление древнеримский политический деятель  Марк Ту́ллий Цицеро́н.
 +
 
 +
Он перевел  на латынь платоновский термин «аналогия», который буквально означал «вновь-отношение», или, как мы говорим, «соотношение».
 +
 
 +
<div class="show-for-large-up">{{center|[[Файл:Scientists_izuchav.mp4|600px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Scientists_izuchav.mp4|600px]]}}</div>
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
 +
==Основные понятия==
 +
'''Пропорция (лат. proportio — соразмерность, выровненность частей) – это равенство двух отношений: [[Файл:Proportion_a_b_cd.png|50px]] или a:b=c:d, где a,b,c,d – не равны нулю, a и  d называют крайними членами пропорции, b и c – средними членами пропорции'''.
 +
 
 +
Например, рассмотрим  равенство 12 : 20 = 3 : 5.   
 +
   
 +
Это пропорция, в которой  крайние члены равны  12 и 5, а средними членами являются числа 20 и 3.  Читается  пропорция так: двенадцать относится к двадцати, как три относится к пяти.
 +
 
 +
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
 +
 
 +
Это означает, что если [[Файл:Proportion_a_b_cd.png|50px]], то ad = bc.
 +
 
 +
Верно и обратное утверждение:  если  произведение  двух  чисел  a и  d  равно  произведению  двух  других чисел  b и c (a≠0,b≠0,c≠0,d≠0), то из этих чисел можно составить пропорцию [[Файл:Proportion_a_b_cd.png|50px]].
 +
 
 +
<div class="textblock">{{center|Из основного свойства пропорции следует, что крайний член пропорции равен произведению средних членов, деленному на известный крайний член пропорции. А средний член пропорции  равен произведению крайних членов, деленному на известный средний член пропорции.}}</div>
 +
 
 +
'''Задачи и задания на пропорции'''
 +
 
 +
'''Задание 1.''' Найдите неизвестный член пропорции.
 +
 
 +
'''Задание 2.''' Из 300 читателей библиотеки 108 человек – студенты. Какой процент всех читателей составляют студенты?
 +
 
 +
'''Задание 3.''' При варке варенья используют ягоды и сахар в отношении 5:2. Сколько надо ягод, если взяли 450 грамм сахара?
 +
 
 +
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 +
  <li class="active">
 +
{{center|[[file:Задание_1.gif]]}}
 +
</li>
 +
<li>
 +
{{center|[[file:Задание_2.gif]]}}
 +
  </li>
 +
<li>
 +
{{center|[[file:Задание_3.gif]]|}}
 +
  </li>
 +
</ul>
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
 +
==Прямая и обратная пропорциональность==
 +
<div class="textblock">{{center|Две взаимно зависимых величины называются пропорциональными, если отношение их величин сохраняется неизменным. Это постоянное отношение пропорциональных величин называется коэффициентом пропорциональности.}}</div>
 +
 
 +
Пример. Масса любого вещества пропорциональна его объёму. Например, 2 литра ртути весят 27.2 кг, 5 литров весят 68 кг, 7 литров весят 95.2 кг. Отношение массы ртути к её объёму (коэффициент пропорциональности) будет равно:
 +
 
 +
<div class="show-for-large-up">{{center|[[Файл:Plotnost_rtuti.png|200px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Plotnost_rtuti.png|200px]]}}</div>
  
−
П р и м е р . Масса любого вещества пропорциональна его объёму. Например, 2 литра ртути весят 27.2 кг, 5 литров весят 68 кг, 7 литров весят 95.2 кг. Отношение массы ртути к её объёму ( коэффициент пропорциональности ) будет равно:
 
−
<div class="show-for-large-up">{{center|[[Файл:Плотность ртути.png|400px]]}}</div>
 
−
<div class="hide-for-large-up">{{center|[[Файл:Плотность ртути.png|400px]]}}</div>
 
 
Таким образом, коэффициентом пропорциональности в данном примере является плотность.
 
Таким образом, коэффициентом пропорциональности в данном примере является плотность.
  
−
'''Пропорцианальность'''. Это простейший вид функциональной зависимости. Различают прямую пропорциональность. (y = kx) и обратную пропорциональность ( y= k/ x). Напр., путь S, пройденный при равномерном движении со скоростью  v, пропорционален времени  t, т. е.  S = vt ; прямо пропорциональна величина основания  y прямоугольника с заданной площадью  a обратно пропорциональна высоте  x, т. е.  y = a/ x.
+
'''Пропорциональность'''. Это простейший вид функциональной зависимости. Различают прямую пропорциональность. (y=kx) и обратную пропорциональность (y=k/x). Например, путь s, пройденный при равномерном движении со скоростью  v, пропорционален времени  t, т. е.  s=vt ; прямо пропорциональна величина основания  y прямоугольника с заданной площадью  a обратно пропорциональна высоте  x, т. е.  y=a/x.
 +
 
 +
<div class="mw-customtoggle-ppol button17">'''Свойства пропорциональности'''</div>
 +
<div class="mw-collapsible mw-collapsed" id="mw-customcollapsible-ppol">
  
 
'''Свойства прямой пропорциональной зависимости.'''  
 
'''Свойства прямой пропорциональной зависимости.'''  
  
 
1. '''Каждому значению х соответствует единственное определенное значение у. (первое свойство прямой пропорциональной зависимости)'''
 
1. '''Каждому значению х соответствует единственное определенное значение у. (первое свойство прямой пропорциональной зависимости)'''
 +
 
2. '''Отношение соответствующих значений величин у и х, связанных прямой пропорциональностью, равно коэффициенту пропорциональности.'''
 
2. '''Отношение соответствующих значений величин у и х, связанных прямой пропорциональностью, равно коэффициенту пропорциональности.'''
 +
 
3. '''Если две величины связаны между собой прямой пропорциональной зависимостью, то при увеличении (уменьшении) одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз.'''
 
3. '''Если две величины связаны между собой прямой пропорциональной зависимостью, то при увеличении (уменьшении) одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз.'''
  
−
{{center|[[Файл:P9.png|class=show-for-large-up|600px]]}}
+
Математической моделью прямой пропорциональной зависимости величин х и у является формула у = кх.
−
{{center|[[Файл:P9.png|class=hide-for-large-up|600px]]}}
 
  
 
'''Свойства обратной пропорциональной зависимости.'''
 
'''Свойства обратной пропорциональной зависимости.'''
  
 
1. '''Каждому значению х (за исключением х=0) соответствует вполне определенное значение у.'''
 
1. '''Каждому значению х (за исключением х=0) соответствует вполне определенное значение у.'''
 +
 
2. '''Произведение соответствующих значений х и у равно коэффициенту обратной пропорциональности.'''
 
2. '''Произведение соответствующих значений х и у равно коэффициенту обратной пропорциональности.'''
 +
 
3. '''Если х увеличивается (уменьшается) в несколько раз, то у уменьшается (увеличивается) во столько же раз, так как их произведение остается неизменным.'''  
 
3. '''Если х увеличивается (уменьшается) в несколько раз, то у уменьшается (увеличивается) во столько же раз, так как их произведение остается неизменным.'''  
  
−
<div class="show-for-large-up">{{center|[[Файл:P10.png|600px]]}}</div>
+
Если х и у связаны обратной пропорциональной зависимостью, то отношение двух любых значений величины х равно обратному отношению соответствующих значений y: x<sub>1</sub>:x<sub>2</sub>=y<sub>2</sub>:y<sub>1</sub>.
−
<div class="hide-for-large-up">{{center|[[Файл:P10.png|600px]]}}</div>
+
 
 +
'''Решение задач'''
 +
 
 +
'''Задача 1.''' Велосипедист, двигаясь с постоянной скоростью, проехал 5 км за 10 минут. Какой путь проедет велосипедист за 45 минут?
 +
 
 +
'''Задача 2.''' Автомобиль ехал 2  часа со скоростью 75 км/ч. За какое время он продет это же расстояние, если будет ехать со скоростью 90 км/ч?
 +
 
 +
<ul class="large-block-grid-2 small-block-grid-1">
 +
    <li>
 +
    [[file:Задача_1.gif]]
 +
  </li>
 +
<li>
 +
    [[file:Задача_2.gif]]
 +
  </li>
 +
</ul>
 +
 
 +
</div>
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
 +
==Золотое сечение==
 +
          '''Геометрия имеет два сокровища: одно из них – Пифагорова теорема,'''
 +
            '''а второе – деление отрезка в среднем и крайнем отношениях...'''
 +
            '''Первое из них можно сравнить с мерой золота, а второе похоже на драгоценный камень.'''
 +
                                                        '''Иоганн Кеплер'''
 +
 
 +
Отрезок прямой можно разделить, как  на две равные части, так  и на две неравные части в любом отношении. Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
 +
 
 +
'''Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему:  a:b=b:c или с:b=b:а'''
  
−
Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.  
+
<div class="show-for-large-up">{{center|[[Файл:Деление_отрезка.gif]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Деление_отрезка.gif]]}}</div>
 +
 
 +
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
 +
 
 +
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если AB принять за единицу, BE = 0,382...
  
−
<div class="show-for-large-up">{{center|[[Файл:P8.png|600px]]}}</div>
+
Для практических целей часто  используют приближенные значения  0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям. Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.
−
<div class="hide-for-large-up">{{center|[[Файл:P8.png|600px]]}}</div>
 
  
−
Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длинна всего отрезка так относится к длине его большей части, как длинна большей части к меньшей. Приближенно это отношение равно 0, 618  ≈5/8. Золотое сечение чаще всего применяется в произведениях искусства, архитектуре, встречается и в природе. 
+
<div class="show-for-large-up">{{center|[[Файл:Деление_отрезка_прямой_по_золотому_сечению.gif]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Деление_отрезка_прямой_по_золотому_сечению.gif]]}}</div>
  
−
Применение «золотого сечения».  
+
Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.  
  
−
У древних основу составляла теория пропорций. Отношение размеров частей человеческого тела связывалось с формулой «золотого сечения». Скульпторы утверждают, что талия делит человеческое тело (образцом которого является Апполон Бельведерский) в отношении «золотого сечения». а:х=1,618.
+
На этой пропорции базируются основные  геометрические фигуры. Прямоугольник с таким отношением сторон стали называть золотым прямоугольником. Разумеется есть и золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618.
  
−
Окружающие предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длинны, близкое к 0,618.
+
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
−
Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В).
+
==Пропорции вокруг нас==
 +
Певучесть скрипки, красота ее голоса находится в прямой зависимости от того, в какой мере форма инструмента согласована с пропорцией золотого сечения. Анализ музыкальных произведений в диапазоне от Баха до Шостаковича продемонстрировал метрические отношения основных разделов музыкальных форм, а также золотое сечение. Таким образом, законы гармонии обнаружены в музыкальных рядах, в таблице Менделеева, в расстояниях между планетами, в микро- и макрокосмосе, во многих областях науки. Скульптура, архитектура, астрономия, биология, техника, психология и т. д. – везде так или иначе проявляет себя золотое сечение.
  
−
<div class="show-for-large-up">{{center|[[Файл:Картинка_3_пропорции.png|300px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Пропорции_вокруг_нас.mp4]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Картинка_3_пропорции.png|300px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Пропорции_вокруг_нас.mp4]]}}</div>
  
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
 
==Полезные ссылки==
 
==Полезные ссылки==
−
В математике отношением называется то частное, которое получается при делении одного числа на другое. Ранее сам этот термин использовался только в тех случаях, когда было необходимо выражение какой-либо одной величины в долях другой, причем такой, которая однородна первой. К примеру, отношения использовались при выражении площади в долях другой площади, длины в долях другой длины и т.п. Решение этой задачи производилось с помощью деления.
+
* Видеоурок на тему «Прямая и обратная пропорциональные зависимости» [Электронный ресурс] //    Znaika  URL:  http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html (дата обращения: 24. 04. 2018)
−
http://simple-math.ru/arithmetics/ratio-proportion.php
+
 
 +
* Видеоурок на тему «Пропорции»: [Электронный ресурс] //    Znaika  URL:  http://znaika.ru/catalog/6-klass/matematika/Proportsii.html (дата обращения: 24. 04. 2018)
 +
 
 +
* Теория пропорций: [Электронный ресурс] //  2006-2018 ФГАУ ГНИИ ИТТ "Информика"  URL: http://files.school-collection.edu.ru/dlrstore/c4d6841c-5a1e-ab8e-3524-e712079e89f0/00145619554921908.htm  (дата обращения: 24. 04. 2018)
  
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
 
==Глоссарий==
 
==Глоссарий==
−
'''Отношение''' – это частное от деления одного числа на другое.
+
'''Отношение''' – это частное от деления одного числа на другое.
 +
 
 +
'''Пропорция''' – это равенство двух отношений.
 +
 
 +
'''Чи́сла Фибона́ччи''' — элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …, в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел.
 +
 
 +
'''Золотое сечение''' (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ, в честь древнегреческого скульптора и архитектора Фидия.Число  Φ  называется также золотым числом.
  
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
== Библиография ==
 
== Библиография ==
−
*Видеоурок на тему «Прямая и обратная пропорциональные зависимости» http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html
+
* Белянин В.С. Владел ли Платон кодом золотой пропорции? Анализ мифа.: [Электронный ресурс] // Академия Тринитаризма URL:  http://www.trinitas.ru/rus/doc/0016/001b/00161296.htm (дата обращения: 24. 04. 2018)
−
*Видеоурок на тему «Пропорции» http://znaika.ru/catalog/6-klass/matematika/Proportsii.html
+
* Золотое сечение: [Электронный ресурс] // МОО «Наука и техника», 1997...2018  URL:  http://n-t.ru/tp/iz/zs (дата обращения: 25. 04. 2018)
 +
* Золотое сечение в дизайне сайтов: [Электронный ресурс] //  2016 UX Guide  URL: http://uxguide.ru/dizajn/zolotoe-sechenie-v-dizajne-sajtov/ (дата обращения: 25. 04. 2018)
 +
* Золотое сечение: [Электронный ресурс] // Блог Рунмастера | © 2006-2018  URL: http://rustimes.com/blog/post_1177437753.html (дата обращения: 25. 04. 2018)
 +
* А. С. Пушкин. Сапожник. Притча: [Электронный ресурс] //Электронная публикация — РВБ, 2000—2018 URL:  http://rvb.ru/pushkin/01text/01versus/0423_36/1829/0521.htm (дата обращения: 25. 04. 2018)
 +
* 15 примеров золотого сечения в архитектуре. Jelena Shiljajeva M.A. in History of Art, University of Glasgow: [Электронный ресурс] //URL: https://arhi1.ru/ob-arhitekture/nauka/zolotoe-sechenie (дата обращения: 25. 04. 2018)
 +
* Ле Корбюзье: [Электронный ресурс] //ArchAndArch.ru 2010-2018  URL:  http://www.archandarch.ru/архитекторы/ле-корбюзье/ (дата обращения: 25. 04. 2018)
 +
* Видеоурок на тему «Прямая и обратная пропорциональные зависимости» [Электронный ресурс] //    Znaika  URL:  http://znaika.ru/catalog/6-klass/matematika/Pryamaya-i-obratnaya-proportsionalnye-zavisimosti.html (дата обращения: 24. 04. 2018)
 +
* Видеоурок на тему «Пропорции»: [Электронный ресурс] //    Znaika  URL:  http://znaika.ru/catalog/6-klass/matematika/Proportsii.html (дата обращения: 24. 04. 2018)
 +
* Теория пропорций: [Электронный ресурс] //  2006-2018 ФГАУ ГНИИ ИТТ "Информика"  URL: http://files.school-collection.edu.ru/dlrstore/c4d6841c-5a1e-ab8e-3524-e712079e89f0/00145619554921908.htm  (дата обращения: 24. 04. 2018)
  
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
Строка 93: Строка 197:
 
<!-- Sidebar -->
 
<!-- Sidebar -->
 
<div class="large-4 medium-5 columns">
 
<div class="large-4 medium-5 columns">
−
<!-- Первый элемент сайдбара Это интересно или топ5/10/15 -->
+
<!-- четвертый элемент сайдбара лайфхак -->
−
<div class="shadow radius sbstyle">
+
<div class="shadow radius sbstyle" style="margin-top:20px;">
 
<div class="row">
 
<div class="row">
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Применение пропорции</div>
+
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Золотая архитектура Кыргызстана</div>
 
</div>
 
</div>
−
<span class="firstcharacter">'''П'''</span><p align="justify">ропорция применяется везде!
 
  
−
{{center|[[Файл:P2.png|800px]]}}<br>
+
Архитектурные комплексы, которые расположены на территории Кыргызстана, занимают значительное место в истории зодчества народов Центральной Азии, соединив в себе лучшие достижения в области строительной техники, архитектуры и декоративного оформления своего времени.  
  
 +
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 +
  <li class="active">
 +
{{center-p|  [[file:Белый_дом._Здание_правительства.jpg|Белый дом. Здание Жогорку Кенеш]]|Белый дом. Здание Жогорку Кенеш}}
 +
  </li>
 +
<li>
 +
{{center-p|  [[file:Бишкекский_Гуманитарный_Университет.jpg|Бишкекский Гуманитарный Университет имени К.Карасаева]]|Бишкекский Гуманитарный Университет имени К.Карасаева}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Гумбез_Манаса._Талас.jpg|Гумбез Манаса. Талас]]|Гумбез Манаса. Талас}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Башня_Бурана.jpg|Башня Бурана]]|Башня Бурана}}
 +
  </li>
 +
<li>
 +
{{center-p|  [[file:Джалал-Абад.jpg|Джалал-Абад]]|Здание Ассамблеи в Чандигархе. Индия}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Дунганская_мечеть._Каракол.jpg|Дунганская мечеть в городе Каракол]]|Дунганская мечеть в городе Каракол}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Караван-сарай_Таш-Рабат.jpg|Караван-сарай Таш-Рабат]]|Караван-сарай Таш-Рабат}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Кыргызская Государственная Филармония1.jpg|Кыргызская Государственная Филармония имени Токтогула Сатылганова]]|Кыргызская Государственная Филармония имени Токтогула Сатылганова}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Кыргызский_государственный_цирк_им._А._Изибаева.jpg|Кыргызский государственный цирк имени А.Изибаева]]|Кыргызский государственный цирк имени А.Изибаева}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Кыргызский национальный академический11 театр оперы и балета имени Малдыбаева.jpg|Кыргызский национальный академический театр оперы и балета имени Абдыласа Малдыбаева]]|Кыргызский национальный академический театр оперы и балета имени Абдыласа Малдыбаева}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Мавзолей_караханидов_XI_–_XII_в.в.jpg|Мавзолей караханидов XI–XIIв.в.]]|Мавзолей караханидов XI–XII в.в.}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Мавзолей_Шах-Фазиль.jpg|Мавзолей Шах-Фазиль]]|Мавзолей Шах-Фазиль}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Международный_Университет_Кыргызстана.jpg|Международный университет Кыргызстана]]|Международный университет Кыргызстана}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Мечеть.Нарын.jpg|Мечеть в городе Нарын]]|Мечеть в городе Нарын}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Мэрия_города_Бишкек.jpg|Мэрия города Бишкек]]|Мэрия города Бишкек}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Площадь Ала-Тоо.Бишкек Кыргызстан.jpg|Площадь Ала-Тоо в городе Бишкек]]|Площадь Ала-Тоо в городе Бишкек}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Площадь_Ала-Тоо.Бишкек.jpg|Площадь Ала-Тоо в городе Бишкек]]|Площадь Ала-Тоо в городе Бишкек}}
 +
  </li>
 +
<li>
 +
{{center-p|  [[file:Узген.Минарет..jpg|Минарет в городе Узген]]|Минарет в городе Узген}}
 +
  </li>
 +
<li>
 +
{{center-p|  [[file:Центральный_портал_мавзолея_караханидов_XI_–_XII_в.в..jpg|Центральный портал мавзолея караханидов XI–XII в.в.]]|Центральный портал мавзолея караханидов XI–XII в.в.}}
 +
  </li>
 +
</ul>
  
−
Например:
+
</div>
  
−
'''1. Пропорция в физике.'''
+
<!-- четвертый элемент сайдбара лайфхак -->
 +
<div class="shadow radius sbstyle" style="margin-top:20px;">
 +
<div class="row">
 +
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Золотое сечение в архитектуре</div>
 +
</div>
 +
Существует  предположение, что знание золотого деления  Пифагор позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера  пользовались соотношениями золотого деления при их создании. Французский архитектор  Шарль Эдуард Ле Корбюзье  нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий, изображенный на рельефе деревянной доски из гробницы  Хесира, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления. Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
  
−
С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т.д. – примеры рычагов. Выигрыш, который дает рычаг в прилагаемом усилии, определяется пропорцией, где M и m – массы грузов, а L и l – «плечи» рычага.
+
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В циркуле, который использовали в Помпеях, также заложены пропорции золотого деления. А термин золотое сечение ввел Леонардо да Винчи (1452-1519 гг)
  
−
{{center|[[Файл:P3.png|800px]]}}<br>
+
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 +
  <li class="active">
 +
{{center-p|[[file:Шарль_Эдуард_Ле_Корбюзье.jpg|Шарль Эдуард Ле Корбюзье]]|Шарль Эдуард Ле Корбюзье}}
 +
  </li>
 +
<li>
 +
    {{center-p|[[file:Храм_фараона_Сети_I.jpg|Храм_фараона_Сети_I]]|Храм_фараона_Сети_I}} 
 +
  </li>
 +
<li>
 +
    {{center-p|[[file:Фараон_Сети_I_и_бог_Анубис._Рельеф_из_храма_Сети_I_в_Абидосе.jpg|Фараон_Сети_I_и_бог_Анубис._Рельеф_из_храма_Сети_I_в_Абидосе]]|Фараон_Сети_I_и_бог_Анубис._Рельеф_из_храма_Сети_I_в_Абидосе}} 
 +
  </li>
 +
<li>
 +
    {{center-p|[[file:Зодчий_на_рельефе_гробницы_Хесира.jpg|Зодчий_на_рельефе_гробницы_Хесира]]|Зодчий_на_рельефе_гробницы_Хесира}} 
 +
  </li>
 +
<li>
 +
    {{center-p|[[file:Парфенон.jpg|Парфенон]]|Парфенон}} 
 +
  </li>
 +
<li>
 +
    {{center-p|[[file:Античный_циркуль.jpg|Античный_циркуль]]|Античный_циркуль}} 
 +
  </li>
 +
</ul>
  
  
−
'''2. Пропорция в географии.'''
+
</div>
  
−
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
+
<!-- Первый элемент сайдбара Это интересно или топ5/10/15 -->
 +
<div class="shadow radius sbstyle">
 +
<div class="row">
 +
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Как построить «Золотой дом» для себя?</div>
 +
</div>
  
−
{{center|[[Файл:P4.png|800px]]}}
+
{{center-p|[[Файл:Золотой_Храм_в_Амритсаре._Индия.jpg|Золотой Храм в Амритсаре. Индия]]|Золотой Храм в Амритсаре. Индия}}
  
−
'''3. Пропорция в музыке.'''
+
Правильное распределение энергий внутри дома, гармоничные конструкции в сочетании с экологией и безопасностью строительных материалов побуждают современных архитекторов и дизайнеров использовать принципы и понятия «Золотого сечения». Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.
  
−
Музыкой греки называли ту часть арифметики, в которой говорится об отношениях и пропорциях. Греки создали и научную теорию. Музыки. Они знали: чем «длиннее» натянутая струна, тем «ниже» получается звук, который она издает; что короткая струна издает высокий звук. Однако у музыкального инструмента не одна, а несколько струн, и для того, чтобы все струны при игре звучали «согласно», приятно для уха, длина звучащих частей их должна быть в определенном отношении. Например, чтобы высоты звуков, издаваемых двумя струнами, различались на октаву, нужно, чтобы их длины относились как 1:2. Подобным образом квинте соответствует отношение 2:3, кварте-отношение 3:4 и т.д.
+
Для талантливых художников и архитекторов правило сохраняется интуитивно во время творческого процесса. Однако некоторые из них сознательно реализуют это положение.
  
−
{{center|[[Файл:P5.png|800px]]}}
+
Известный французский архитектор  Шарль Эдуард Ле Корбюзье  для расчёта параметров будущего дома и интерьера использовал в качестве отправной единицы рост хозяина. Все его работы по-настоящему индивидуальны и гармоничны.
  
−
'''4. Пропорции в архитектуре'''
+
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 +
  <li class="active">
 +
{{center-p| [[file:Здание_Ассамблеи_в_Чандигархе._Индия.jpg|Здание Ассамблеи в Чандигархе. Индия]]|Здание Ассамблеи в Чандигархе. Индия}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Фото_1__Здание_Ассамблеи_в_Чандигархе._Индия1.jpg|Здание Ассамблеи в Чандигархе. Индия]]|Здание Ассамблеи в Чандигархе. Индия}}
 +
  </li>
 +
<li>
 +
{{center-p|    [[file:Фото_Здание_Ассамблеи_в_Чандигархе._Индия2.jpg|Здание Ассамблеи в Чандигархе. Индия]]|Здание Ассамблеи в Чандигархе. Индия}}
 +
  </li>
 +
</ul>
  
−
Пропорции в архитектуре – это ее внутренняя красота.  
+
В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали. Для этого достаточно переставить мебель или сделать дополнительную перегородку. Аналогичным образом меняется высота и длина окон и дверей.
  
−
ПАРФЕНОН, храм Афины Парфенос на Акрополе в Афинах, памятник древнегреческой высокой классики. Мраморный дорический периптер с ионическим скульптурным фризом (447-438 до н. э., архитекторы Иктин и Калликрат) замечателен величественной красотой форм и пропорций. Статуи фронтонов, рельефы метоп и фриза (окончены в 432 до н. э.) созданы под руководством Фидия. Разрушен в 1687; частично восстановлен. Отношение высоты здания к его длине равно 0, 618.
+
{{center-p|[[Файл:Шкаф-перегородка.jpg|Шкаф-перегородка]]|Шкаф-перегородка}}
  
−
{{center|[[Файл:P6.png|800px]]}}
+
В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.
  
−
'''5. Пропорции в скульптуре.'''
+
{{center-p|[[Файл:Вариант_освещения_комнаты.jpg|Вариант освещения комнаты]]|Вариант освещения комнаты}}
  
−
АПОЛЛОН БЕЛЬВЕДЕРСКИЙ, статуя Аполлона — мраморная римская копия бронзового оригинала работы древнегреческого скульптора Леохара  (ок. 330-320 до н. э., Музей Пио-Клементино, Ватикан). Название от ватиканского дворца Бельведер, где выставлена статуя. Долгое время считалась вершиной греческого искусства. На рисунке представлена статуя Аполлона Бельведерского, разделенная в отношении (точка С делит отрезок АD, точка В делит отрезок АС)
+
Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.
  
−
{{center|[[Файл:P7.png|800px]]}}
+
Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.
  
 +
</div>
  
−
</p>
 
−
</div>
 
  
  
Строка 146: Строка 345:
 
<div class="shadow radius sbstyle" style="margin-top:20px;">
 
<div class="shadow radius sbstyle" style="margin-top:20px;">
 
<div class="row">
 
<div class="row">
−
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Главное правило пропорции</div>
+
<div class="large-10 small-10 large-centered small-centered columns rubric" style="background-color:lightgrey;">Запомнить правило легко</div>
 
</div>
 
</div>
−
 
−
 
 
Есть у пропорции правило главное
 
Есть у пропорции правило главное
  
Строка 158: Строка 355:
 
Будут всегда эти числа равны.
 
Будут всегда эти числа равны.
  
 +
</div>
 +
<div class="sbstyle">
 +
<div class="row">
 +
<div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Пройди тестирование</div>
 +
</div>
 +
 +
</div>
 +
</div>
  
−
</div>
+
{{lang|:KR:Математика: Катыш жана пропорция}}
−
{{lang|:KR:Математика: Бөлчөктүк сандар}}
 
 
[[Category:Средняя школа]]
 
[[Category:Средняя школа]]
 
[[Category:Математика]]
 
[[Category:Математика]]

Текущая версия на 08:45, 22 октября 2018

История развития учения о пропорции

          Ничто не нравится, кроме красоты, в красоте – ничто, кроме форм, в формах – ничто, 
             кроме пропорций, в пропорциях – ничто, кроме числа.
                                                           Аврелий Августин
Понятие пропорции как равенства двух отношений чисел для целых чисел было дано в глубокой древности. Еще древние вавилоняне пришли к понятию пропорциональности сторон подобных треугольников, выраженных в целых числах.

Впервые интерес к пропорции, образующейся при делении отрезка в крайнем и среднем отношении, возникает в античной науке.

Так в Древней Греции, славившейся произведениями искусства, архитектуры, различными ремеслами, успешно развивалось учение об отношениях и пропорциях. С ними связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Принято считать, что понятие о делении отрезка ввел в научный обиход Пифагор, древнегреческий философ и математик. Он и его ученики рассматривали три вида пропорций:

  • Арифметическую: а - b = с - d
  • Геометрическую: a : b = c : d
  • Гармоническую: a : b = b : (a - b)

Другой древнегреческий ученый Платон сводил сущность пропорции к тому, что «для соединения двух частей с третьей совершенным образом необходима пропорция, которая бы «скрепила» их в единое целое. При этом одна часть целого должна так относиться к другой, как целое к большей части. Такая пропорция отвечает гармоническому соединению, она и является золотой».

А древнегреческий ученый Евдокс дал систематическое учение о пропорциях применительно не только к целым, но и к дробным числам. Строгая теория пропорций была построена в 3 веке до н.э. древнегреческим геометром Евклидом в его знаменитых «Началах», состоящих из 13 книг. Этой теории он посвящает 5 книг. В основу своей теории Евклид положил учение Евдокса. В настоящее время теория пропорций мало отличается от теории Евдокса – Евклида. Евклид определяет сравнение между пропорциями: отношение a : b меньше, чем отношение c : d, если есть такие числа m и n, если ma > nb и в то же время mc ≤ nd. А читается она так: «В верной пропорции произведение крайних членов равно произведению средних». Математические свойства пропорции уже тогда создавали вокруг нее ореол таинственности и мистического поклонения. Удивителен тот факт, что слово «пропорция» ввел в употребление древнеримский политический деятель Марк Ту́ллий Цицеро́н.

Он перевел на латынь платоновский термин «аналогия», который буквально означал «вновь-отношение», или, как мы говорим, «соотношение».

В начало

Основные понятия

Пропорция (лат. proportio — соразмерность, выровненность частей) – это равенство двух отношений: Proportion a b cd.png или a:b=c:d, где a,b,c,d – не равны нулю, a и d называют крайними членами пропорции, b и c – средними членами пропорции.

Например, рассмотрим равенство 12 : 20 = 3 : 5.

Это пропорция, в которой крайние члены равны 12 и 5, а средними членами являются числа 20 и 3. Читается пропорция так: двенадцать относится к двадцати, как три относится к пяти.

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

Это означает, что если Proportion a b cd.png, то ad = bc.

Верно и обратное утверждение: если произведение двух чисел a и d равно произведению двух других чисел b и c (a≠0,b≠0,c≠0,d≠0), то из этих чисел можно составить пропорцию Proportion a b cd.png.

Из основного свойства пропорции следует, что крайний член пропорции равен произведению средних членов, деленному на известный крайний член пропорции. А средний член пропорции равен произведению крайних членов, деленному на известный средний член пропорции.

Задачи и задания на пропорции

Задание 1. Найдите неизвестный член пропорции.

Задание 2. Из 300 читателей библиотеки 108 человек – студенты. Какой процент всех читателей составляют студенты?

Задание 3. При варке варенья используют ягоды и сахар в отношении 5:2. Сколько надо ягод, если взяли 450 грамм сахара?

  • Задание 1.gif
  • Задание 2.gif
  • Задание 3.gif
В начало

Прямая и обратная пропорциональность

Две взаимно зависимых величины называются пропорциональными, если отношение их величин сохраняется неизменным. Это постоянное отношение пропорциональных величин называется коэффициентом пропорциональности.

Пример. Масса любого вещества пропорциональна его объёму. Например, 2 литра ртути весят 27.2 кг, 5 литров весят 68 кг, 7 литров весят 95.2 кг. Отношение массы ртути к её объёму (коэффициент пропорциональности) будет равно:

Plotnost rtuti.png
Plotnost rtuti.png

Таким образом, коэффициентом пропорциональности в данном примере является плотность.

Пропорциональность. Это простейший вид функциональной зависимости. Различают прямую пропорциональность. (y=kx) и обратную пропорциональность (y=k/x). Например, путь s, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. s=vt ; прямо пропорциональна величина основания y прямоугольника с заданной площадью a обратно пропорциональна высоте x, т. е. y=a/x.

Свойства пропорциональности

Свойства прямой пропорциональной зависимости.

1. Каждому значению х соответствует единственное определенное значение у. (первое свойство прямой пропорциональной зависимости)

2. Отношение соответствующих значений величин у и х, связанных прямой пропорциональностью, равно коэффициенту пропорциональности.

3. Если две величины связаны между собой прямой пропорциональной зависимостью, то при увеличении (уменьшении) одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз.

Математической моделью прямой пропорциональной зависимости величин х и у является формула у = кх.

Свойства обратной пропорциональной зависимости.

1. Каждому значению х (за исключением х=0) соответствует вполне определенное значение у.

2. Произведение соответствующих значений х и у равно коэффициенту обратной пропорциональности.

3. Если х увеличивается (уменьшается) в несколько раз, то у уменьшается (увеличивается) во столько же раз, так как их произведение остается неизменным.

Если х и у связаны обратной пропорциональной зависимостью, то отношение двух любых значений величины х равно обратному отношению соответствующих значений y: x1:x2=y2:y1.

Решение задач

Задача 1. Велосипедист, двигаясь с постоянной скоростью, проехал 5 км за 10 минут. Какой путь проедет велосипедист за 45 минут?

Задача 2. Автомобиль ехал 2 часа со скоростью 75 км/ч. За какое время он продет это же расстояние, если будет ехать со скоростью 90 км/ч?

  • Задача 1.gif
  • Задача 2.gif
В начало

Золотое сечение

         Геометрия имеет два сокровища: одно из них – Пифагорова теорема, 
            а второе – деление отрезка в среднем и крайнем отношениях... 
            Первое из них можно сравнить с мерой золота, а второе похоже на драгоценный камень. 
                                                        Иоганн Кеплер

Отрезок прямой можно разделить, как на две равные части, так и на две неравные части в любом отношении. Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему: a:b=b:c или с:b=b:а

Деление отрезка.gif
Деление отрезка.gif

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если AB принять за единицу, BE = 0,382...

Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям. Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.

Деление отрезка прямой по золотому сечению.gif
Деление отрезка прямой по золотому сечению.gif

Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.

На этой пропорции базируются основные геометрические фигуры. Прямоугольник с таким отношением сторон стали называть золотым прямоугольником. Разумеется есть и золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618.

В начало

Пропорции вокруг нас

Певучесть скрипки, красота ее голоса находится в прямой зависимости от того, в какой мере форма инструмента согласована с пропорцией золотого сечения. Анализ музыкальных произведений в диапазоне от Баха до Шостаковича продемонстрировал метрические отношения основных разделов музыкальных форм, а также золотое сечение. Таким образом, законы гармонии обнаружены в музыкальных рядах, в таблице Менделеева, в расстояниях между планетами, в микро- и макрокосмосе, во многих областях науки. Скульптура, архитектура, астрономия, биология, техника, психология и т. д. – везде так или иначе проявляет себя золотое сечение.

В начало

Полезные ссылки

В начало

Глоссарий

Отношение – это частное от деления одного числа на другое.

Пропорция – это равенство двух отношений.

Чи́сла Фибона́ччи — элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …, в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел.

Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ, в честь древнегреческого скульптора и архитектора Фидия.Число Φ называется также золотым числом.

В начало

Библиография

В начало

Золотая архитектура Кыргызстана

Архитектурные комплексы, которые расположены на территории Кыргызстана, занимают значительное место в истории зодчества народов Центральной Азии, соединив в себе лучшие достижения в области строительной техники, архитектуры и декоративного оформления своего времени.

  • Белый дом. Здание Жогорку Кенеш
  • Бишкекский Гуманитарный Университет имени К.Карасаева
  • Гумбез Манаса. Талас
  • Башня Бурана
  • Джалал-Абад
  • Дунганская мечеть в городе Каракол
  • Караван-сарай Таш-Рабат
  • Кыргызская Государственная Филармония имени Токтогула Сатылганова
  • Кыргызский государственный цирк имени А.Изибаева
  • Кыргызский национальный академический театр оперы и балета имени Абдыласа Малдыбаева
  • Мавзолей караханидов XI–XIIв.в.
  • Мавзолей Шах-Фазиль
  • Международный университет Кыргызстана
  • Мечеть в городе Нарын
  • Мэрия города Бишкек
  • Площадь Ала-Тоо в городе Бишкек
  • Площадь Ала-Тоо в городе Бишкек
  • Минарет в городе Узген
  • Центральный портал мавзолея караханидов XI–XII в.в.
Золотое сечение в архитектуре

Существует предположение, что знание золотого деления Пифагор позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Шарль Эдуард Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий, изображенный на рельефе деревянной доски из гробницы Хесира, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления. Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В циркуле, который использовали в Помпеях, также заложены пропорции золотого деления. А термин золотое сечение ввел Леонардо да Винчи (1452-1519 гг)

  • Шарль Эдуард Ле Корбюзье
  • Храм_фараона_Сети_I
  • Фараон_Сети_I_и_бог_Анубис._Рельеф_из_храма_Сети_I_в_Абидосе
  • Зодчий_на_рельефе_гробницы_Хесира
  • Парфенон
  • Античный_циркуль


Как построить «Золотой дом» для себя?
Золотой Храм в Амритсаре. Индия


Правильное распределение энергий внутри дома, гармоничные конструкции в сочетании с экологией и безопасностью строительных материалов побуждают современных архитекторов и дизайнеров использовать принципы и понятия «Золотого сечения». Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.

Для талантливых художников и архитекторов правило сохраняется интуитивно во время творческого процесса. Однако некоторые из них сознательно реализуют это положение.

Известный французский архитектор Шарль Эдуард Ле Корбюзье для расчёта параметров будущего дома и интерьера использовал в качестве отправной единицы рост хозяина. Все его работы по-настоящему индивидуальны и гармоничны.

  • Здание Ассамблеи в Чандигархе. Индия
  • Здание Ассамблеи в Чандигархе. Индия
  • Здание Ассамблеи в Чандигархе. Индия

В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали. Для этого достаточно переставить мебель или сделать дополнительную перегородку. Аналогичным образом меняется высота и длина окон и дверей.

Шкаф-перегородка


В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.

Вариант освещения комнаты


Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.

Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.


Запомнить правило легко

Есть у пропорции правило главное

Все его знать и запомнить должны

Средние члены умножишь и крайние

Будут всегда эти числа равны.

Пройди тестирование
Пройди тестирование
Источник — «https://bb.edu.gov.kg/index.php?title=Математика:_Отношения_и_пропорции&oldid=27425»