БИЛИМ БУЛАГЫ

Математика: Действия над натуральными числами — различия между версиями

(→‎Библиография)
 
(не показано 56 промежуточных версий 2 участников)
Строка 2: Строка 2:
 
{{Якорь|Начало}}
 
{{Якорь|Начало}}
 
<div class="row  phis-bg"><div class="maintext large-8 medium-7 columns"><!-- Page Content -->
 
<div class="row  phis-bg"><div class="maintext large-8 medium-7 columns"><!-- Page Content -->
−
<div class="cutok">[[#Свойства сложения|Свойства сложения]] [[#Свойства вычитания|Свойства вычитания]] [[#Свойства умножения|Свойства умножения]] [[#Свойства деления|Свойства деления]]</div>
+
 
  
  
 
Для натуральных чисел определены следующие действия: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Только в результате двух действий получаются также натуральные числа. Это сложение и умножение.
 
Для натуральных чисел определены следующие действия: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Только в результате двух действий получаются также натуральные числа. Это сложение и умножение.
  
−
<div class="show-for-large-up">{{center|[[Файл:Действия_над_натуральными_числами.gif|600px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Deystviya_nad_natural_numbers.gif|600px]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Действия_над_натуральными_числами.gif|600px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Deystviya_nad_natural_numbers.gif|600px]]}}</div>
  
 
'''Свойства  арифметических действий'''
 
'''Свойства  арифметических действий'''
Строка 16: Строка 16:
 
==Свойства сложения==
 
==Свойства сложения==
 
1. Переместительное свойство сложения: от перестановки слагаемых сумма не меняется.  
 
1. Переместительное свойство сложения: от перестановки слагаемых сумма не меняется.  
−
                                    a + b = b + a.
+
<center>a + b = b + a </center>
 
В этом равенстве a и  b могут принимать любые натуральные значения и значение 0.
 
В этом равенстве a и  b могут принимать любые натуральные значения и значение 0.
  
Строка 22: Строка 22:
  
 
В буквенном виде:  
 
В буквенном виде:  
−
                                (a + b) + c = a + (b + c)
+
<center>(a + b) + c = a + (b + c)</center>
  
 
Так как результат сложения трёх чисел не зависит от того как поставлены скобки, то скобки можно не ставить и писать просто a + b + с.
 
Так как результат сложения трёх чисел не зависит от того как поставлены скобки, то скобки можно не ставить и писать просто a + b + с.
  
−
                                (a + b) + c = a + (b + c) = a + b + c
+
<center>(a + b) + c = a + (b + c) = a + b + c</center>
 
Переместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм.
 
Переместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм.
  
Строка 34: Строка 34:
  
 
Если к числу прибавить нуль, получится само число.
 
Если к числу прибавить нуль, получится само число.
−
                                a + О = О + a = a.
+
<center>a + О = О + a = a</center>
  
  
−
<div class="show-for-large-up">{{center|[[Файл:Пример_1_действия_над_натуральными_числами.gif|600px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Example_1_deystviya_nad_nat_numbers.gif|600px]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Пример_1_действия_над_натуральными_числами.gif|600px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Example_1_deystviya_nad_nat_numbers.gif|600px]]}}</div>
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
 
==Свойства вычитания==
 
==Свойства вычитания==
 
1. Свойство вычитания суммы из числа
 
1. Свойство вычитания суммы из числа
 
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.  
 
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.  
−
                                a − (b + c) = (a − b) – c    или    a − (b + c) = (a − с) – b.
+
<center>a − (b + c) = (a − b) – c    или    a − (b + c) = (a − с) – b</center>
  
 
2. Скобки в выражении (a − b) − c не имеют значения и их можно опустить.  
 
2. Скобки в выражении (a − b) − c не имеют значения и их можно опустить.  
−
                                (a − b) − c = a − b – c.
+
<center>(a − b) − c = a − b – c</center>
  
 
3. Свойство вычитания числа из суммы
 
3. Свойство вычитания числа из суммы
Строка 52: Строка 54:
 
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
 
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
  
−
                              (a + b) − c = (a − c) + b (если a > c или а = с)  
+
<center>(a+b)−c=(a−c)+b (если a>c или а=с) или (a + b) − c = (b − c) + a (если b > c или b = с) </center>
−
                                                        или  
 
−
                                (a + b) − c = (b − c) + a (если b > c или b = с)
 
  
 
4. Свойство нуля при вычитании
 
4. Свойство нуля при вычитании
 
Если из числа вычесть нуль, получится само число.   
 
Если из числа вычесть нуль, получится само число.   
−
                              a − О = a.
+
<center>a − О = a</center>
 
Если из числа вычесть само число, то получится нуль.   
 
Если из числа вычесть само число, то получится нуль.   
−
                              a − a = О.
+
<center>a − a = О</center>
  
−
<div class="show-for-large-up">{{center|[[Файл:Пример_2_действия_над_натуральными_числами.gif|600px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Example_2_Deystviya_nad_nat_numbers.gif|600px]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Пример_2_действия_над_натуральными_числами.gif|600px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Example_2_Deystviya_nad_nat_numbers.gif|600px]]}}</div>
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
 
==Свойство умножения==
 
==Свойство умножения==
 
1. Переместительное свойство умножения
 
1. Переместительное свойство умножения
 
От перестановки множителей произведение не меняется.  
 
От перестановки множителей произведение не меняется.  
−
                                    a • b = b • a
+
 
 +
<center> a • b = b • a </center>
  
 
2. Сочетательное свойство умножения
 
2. Сочетательное свойство умножения
 
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
 
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
−
                                  a • (b • c) = (a • b) • c.
+
 
 +
<center>a • (b • c) = (a • b) • c </center>
  
 
3. Свойство нуля при умножении
 
3. Свойство нуля при умножении
 
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
 
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
−
                                a ∙ О = a,
+
 
−
                                О • a • b • c = О.
+
<center>a ∙ О = a </center>
 +
<center>О • a • b • c = О </center>
  
 
'''Распределительное свойство умножения относительно сложения'''
 
'''Распределительное свойство умножения относительно сложения'''
  
 
Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.  
 
Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.  
−
                                (a + b) • c = a • c + b • c
+
 
 +
<center> (a + b) • c = a • c + b • c </center>
  
 
Это свойство справедливо для любого количества слагаемых.  
 
Это свойство справедливо для любого количества слагаемых.  
−
                              (a + b + с + d) • k = a • k + b • k + c • k + d • k.
+
 
 +
<center> (a + b + с + d) • k = a • k + b • k + c • k + d • k </center>
  
 
'''Распределительное свойство умножения относительно вычитания'''
 
'''Распределительное свойство умножения относительно вычитания'''
Строка 91: Строка 98:
 
1. Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.
 
1. Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.
 
В буквенном виде свойство записывается так:   
 
В буквенном виде свойство записывается так:   
−
                              (a − b) • c = a • c − b • c
+
 
 +
<center>(a − b) • c = a • c − b • c </center>
  
 
2. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
 
2. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
  
−
<div class="show-for-large-up">{{center|[[Файл:Пример_3_действия_над_натуральными_числами_.gif|600px]]}}</div>
+
<div class="show-for-large-up">{{center|[[Файл:Example_3_Deystviya_nad_nat_numbers.gif|600px]]}}</div>
−
<div class="hide-for-large-up">{{center|[[Файл:Пример_3_действия_над_натуральными_числами_.gif|600px]]}}</div>
+
<div class="hide-for-large-up">{{center|[[Файл:Example_3_Deystviya_nad_nat_numbers.gif|600px]]}}</div>
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
 
==Свойство деления==
 
==Свойство деления==
Строка 102: Строка 112:
  
 
2. При делении нуля на число получается ноль.  
 
2. При делении нуля на число получается ноль.  
−
                                  О : a = О
+
 +
<center>О : a = О</center>
  
 
3. При делении любого числа на 1 получается это же число.  
 
3. При делении любого числа на 1 получается это же число.  
−
                                  b : 1 = b
+
 +
<center>b : 1 = b</center>
  
 
4. Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
 
4. Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
−
                                  a : b = (a • k) : (b • k), где k — любое натуральное число.
 
  
−
<div class="show-for-large-up">{{center|[[Файл:Пример_4_действия_над_натуральными_числами.gif|600px]]}}</div>
+
<center>a : b = (a • k) : (b • k), где k — любое натуральное число. </center>
−
<div class="hide-for-large-up">{{center|[[Файл:Пример_4_действия_над_натуральными_числами.gif|600px]]}}</div>
 
  
−
==Полезные ссылки==
+
<div class="show-for-large-up">{{center|[[Файл:Example_4_Deystviya_nad_nat_numbers.gif|600px]]}}</div>
−
А знаете ли вы, что раньше  за незнание математики, человека могли просто уволить с работы? Нет?! Тогда стоит посмотреть передачу об истории возникновения таблицы умножения. Профессор рассказывает об интересном методе умножения в Древнем Египте, знакомит с «пальцевым» способом умножения на девять. Кроме того, проводится связь между геометрией и строительством пчелиных сот. Весёлая задачка посвящена умножению. https://www.youtube.com/watch?v=vcKD1SURjfg
+
<div class="hide-for-large-up">{{center|[[Файл:Example_4_Deystviya_nad_nat_numbers.gif|600px]]}}</div>
  
−
==Глоссарий==
+
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
−
'''Действие''' – это математический процесс, в котором по некоторому правилу и двум данным числам определяют третье число.
 
  
 
==Примеры в несколько действий==
 
==Примеры в несколько действий==
Строка 133: Строка 142:
 
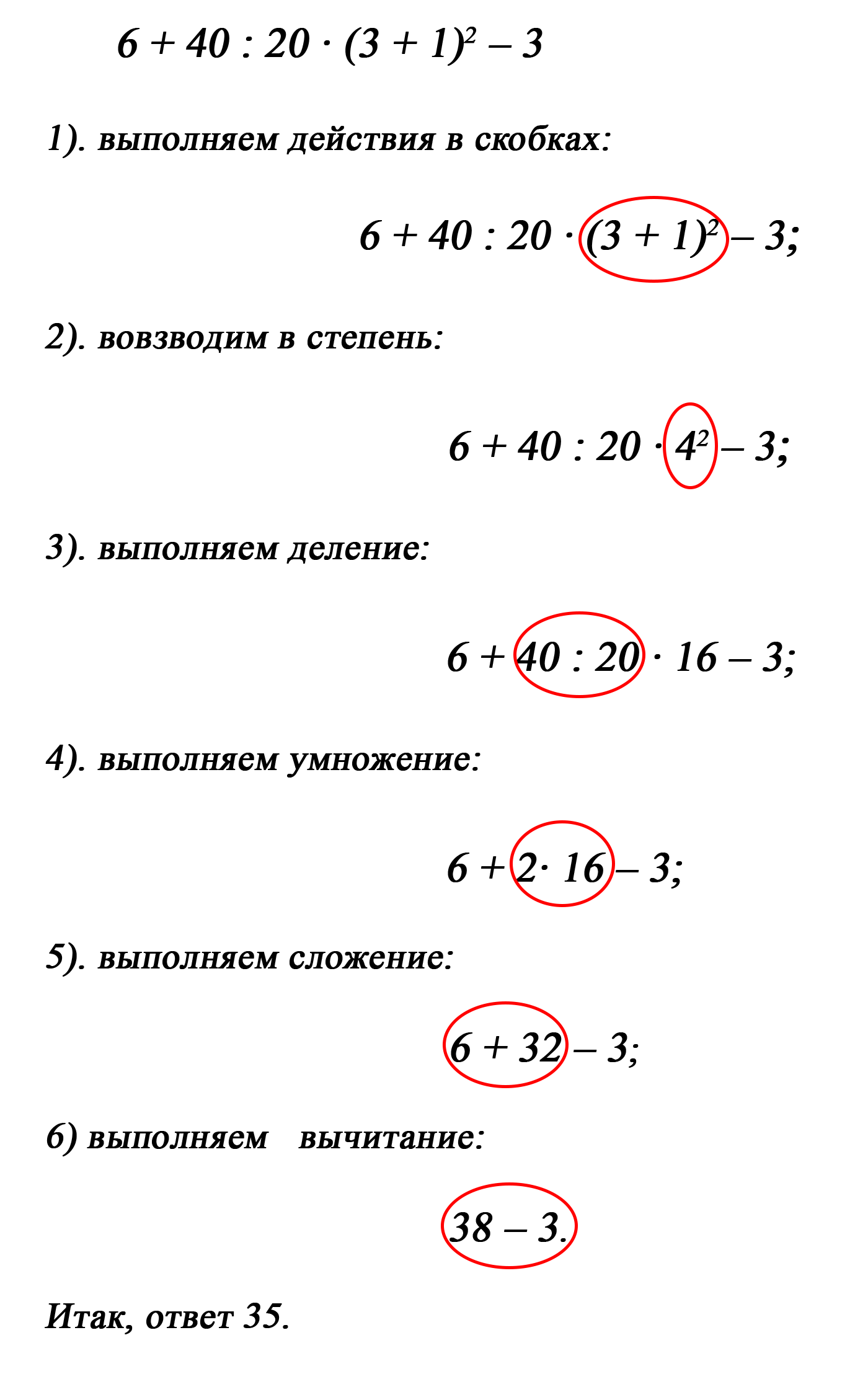
В выражениях, содержащих различные действия, сначала выполняется действие в скобках, затем последовательно по уменьшению старшинства: возведение в степень – деление – умножение – сложение – вычитание.
 
В выражениях, содержащих различные действия, сначала выполняется действие в скобках, затем последовательно по уменьшению старшинства: возведение в степень – деление – умножение – сложение – вычитание.
  
−
Например, найдем значение выражения:  
+
<div class="show-for-large-up">{{center|[[Файл:Example_poryadok_act.png|400px]]}}</div>
 +
<div class="hide-for-large-up">{{center|[[Файл:Example_poryadok_act.png|400px]]}}</div>
  
−
<div class="show-for-large-up">{{center|[[Файл:Пример__порядок_действий.png|400px]]}}</div>
+
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
−
<div class="hide-for-large-up">{{center|[[Файл:Пример__порядок_действий.png|400px]]}}</div>
+
 
 +
==Глоссарий==
 +
'''Действие''' – это математический процесс, в котором по некоторому правилу и двум данным числам определяют третье число.
 +
 
 +
'''Сво́йство'''  — атрибут предмета (объекта).
 +
 
 +
'''Степенью числа a с натуральным показателем n, бóльшим 1''', называется произведение  n одинаковых множителей, каждый из которых равен числу a.              a∙a ∙ a∙…∙a=a<sup>n</sup>
 +
 
 +
'''Корнем n - й степени из числа a'''  называется  такое число b, где  b<sup>n</sup>=a,  где  n>1
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
 +
 
 +
==Полезные ссылки==
 +
А знаете ли вы, что раньше за незнание математики, человека могли просто уволить с работы? Нет?! Тогда стоит посмотреть передачу об истории возникновения таблицы умножения. Профессор рассказывает об интересном методе умножения в Древнем Египте, знакомит с «пальцевым» способом умножения на девять. Кроме того, проводится связь между геометрией и строительством пчелиных сот. Весёлая задачка посвящена умножению. : [Электронный ресурс] //Академия Занимательных Наук YouTube, 2017. https://www.youtube.com/watch?v=vcKD1SURjfg . (дата обращения: 20.11.2017)
 +
 
 +
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
 
== Библиография ==
 
== Библиография ==
Строка 147: Строка 172:
 
*Кроссворды для школьников. Математика. Мантуленко В.Г., Гетменко О.Г. –Ярославль: «Академия развития», 1998. – 144 с.
 
*Кроссворды для школьников. Математика. Мантуленко В.Г., Гетменко О.Г. –Ярославль: «Академия развития», 1998. – 144 с.
  
−
<div class="light" style="float:right;>[[#Начало|В начало]]</div>
+
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all />
  
 
</div>
 
</div>
Строка 165: Строка 190:
 
В национальной игре ордо (эмоциональная игра у взрослых кыргызов, воспроизводящая бой за захват ханской ставки), в детской игре в альчики математические действия сложения, умножения в уме производили с помощью понятия бирдин үчү— пять; бирдин үчү— пять альчиков, бирдин үчү бир — шесть альчиков, бирдин үчү эки — семь альчиков, экинин үчү — десять альчиков, экинин үчү торт — четырнадцать альчиков, бештин үчү — двадцать пять альчиков, кырктын үчү — двести альчиков.
 
В национальной игре ордо (эмоциональная игра у взрослых кыргызов, воспроизводящая бой за захват ханской ставки), в детской игре в альчики математические действия сложения, умножения в уме производили с помощью понятия бирдин үчү— пять; бирдин үчү— пять альчиков, бирдин үчү бир — шесть альчиков, бирдин үчү эки — семь альчиков, экинин үчү — десять альчиков, экинин үчү торт — четырнадцать альчиков, бештин үчү — двадцать пять альчиков, кырктын үчү — двести альчиков.
  
−
<div class="show-for-large-up">{{center|[[Файл:Др_кырг_натуральные_числа_действия_альчики.jpg|800px|Национальная игра в альчики]]}}</div>
+
{{center|[[Файл:Game_alchik.jpg|800px|Национальная игра в альчики]]}}
−
<div class="hide-for-large-up">{{center|[[Файл:Др_кырг_натуральные_числа_действия_альчики.jpg|800px|Национальная игра в альчики]]}}</div>
 
  
−
Древняя игра кыргызов «Тогуз кумалак» или «Тогуз коргоол» (десять маленьких орешков или фишек) представляет собой деревянную доску с 18 маленькими лунками (в каждой по 9 фишек) для непосредственной игры и большими лунками для выигранных фишек (орешков):
+
Древняя игра кыргызов «Тогуз кумалак» или «Тогуз коргоол» (девять маленьких орешков или фишек) представляет собой деревянную доску с 18 маленькими лунками (в каждой по 9 фишек) для непосредственной игры и большими лунками для выигранных фишек (орешков):
  
 
<center>''Эки атасы бар,'' <br>
 
<center>''Эки атасы бар,'' <br>
Строка 183: Строка 207:
 
Расчет и тактика игроков заключались в том, что каждый из них не должен сделать ошибочного хода и тем самым дать возможность другой стороне собрать большое количество фишек. Кто из двух играющих соперников обладал аналитическим умом и тактикой хитроумных ходов, тот и становился победителем.  
 
Расчет и тактика игроков заключались в том, что каждый из них не должен сделать ошибочного хода и тем самым дать возможность другой стороне собрать большое количество фишек. Кто из двух играющих соперников обладал аналитическим умом и тактикой хитроумных ходов, тот и становился победителем.  
  
−
<div class="show-for-large-up">{{center|[[Файл:Др_кырг_натуральные_числа_действия.jpg|800px|«Тогуз кумалак» или «Тогуз коргоол»]]}}</div>
+
{{center|[[Файл:Game_toguz_korgool.jpg|800px|«Тогуз кумалак» или «Тогуз коргоол»]]}}
−
<div class="hide-for-large-up">{{center|[[Файл:Др_кырг_натуральные_числа_действия.jpg|800px|«Тогуз кумалак» или «Тогуз коргоол»]]}}</div>
 
−
 
 
  
 
Другая, более сложная чем «Тогуз кумалак» игра древних кыргызов именовалась «Чатыраш»:
 
Другая, более сложная чем «Тогуз кумалак» игра древних кыргызов именовалась «Чатыраш»:
Строка 206: Строка 228:
  
 
Вы спросите, зачем такие сложности? Ведь есть калькулятор в мобильном телефоне. Да, без проблем, но представьте ситуацию, телефон разрядился, или вы не хотите показаться глупым человеком в магазине и хотите правильно получить сдачу? Тогда предлагаем посмотреть видео сюжет, где раскроют секреты, как научится быстро считать.
 
Вы спросите, зачем такие сложности? Ведь есть калькулятор в мобильном телефоне. Да, без проблем, но представьте ситуацию, телефон разрядился, или вы не хотите показаться глупым человеком в магазине и хотите правильно получить сдачу? Тогда предлагаем посмотреть видео сюжет, где раскроют секреты, как научится быстро считать.
−
<div class="show-for-large-up">{{center|[[Файл:Как научиться быстро считать.mp4|450px]]}}</div>
+
{{center|[[Файл:Kak_nauchitsya_bystro_count.mp4|450px]]}}
−
<div class="hide-for-large-up">{{center|[[Файл:Как научиться быстро считать.mp4|450px]]}}</div>
 
−
 
 
  
 
</div>
 
</div>
Строка 224: Строка 244:
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
 
   <li class="active">
 
   <li class="active">
−
     [[file: Кроссворд_задание.jpg|450px]]
+
     [[file:New_krossword.jpg|450px]]
 
   </li>
 
   </li>
 
  <li>
 
  <li>
−
     [[file: Кроссворд_ответы.jpg|450px]]
+
     [[file:Krossword_deystviya_nad_nat_numbers.jpg|450px]]
 
   </li>
 
   </li>
 
</ul>
 
</ul>
Строка 245: Строка 265:
 
Предлагаем вашему вниманию самые  распространенные пословицы и поговорки с числами. Подумайте, какой смысл они несут.
 
Предлагаем вашему вниманию самые  распространенные пословицы и поговорки с числами. Подумайте, какой смысл они несут.
  
−
<div class="show-for-large-up">{{center|[[Файл:Пословицы_и_поговорки.jpg|450px]]}}</div>
+
<ul class=" example-orbit" data-orbit="" data-options="animation:slide; pause_on_hover:true; animation_speed:500; navigation_arrows:true; resume_on_mouseout: true; timer_speed:4500;" >
−
<div class="hide-for-large-up">{{center|[[Файл:Пословицы_и_поговорки.jpg|450px]]}}</div>
+
  <li class="active">
 +
    [[file:Poslovicy_i_pogovorki_1-3.jpg|450px]]
 +
  </li>
 +
<li>
 +
    [[file:Poslovicy_i_pogovorki_4_6.jpg|450px]]
 +
  </li>
 +
<li>
 +
    [[file:Poslovicy_i_pogovorki_7_9.jpg|450px]]
 +
  </li>
 +
</ul>
  
 
</div>
 
</div>
−
 
+
<div class="sbstyle">
 +
<div class="row">
 +
<div class="large-10 small-10 large-centered small-centered columns rubric" style="margin-top:20px">Пройди тестирование</div>
 +
</div>
 +
 +
</div>
 
</div>
 
</div>
  
 
{{lang|:KR:Математика: Натуралдык сандар менен болгон амалдар}}
 
{{lang|:KR:Математика: Натуралдык сандар менен болгон амалдар}}
 
[[Category:Средняя школа]]
 
[[Category:Средняя школа]]
−
[[Category:Математика: Натуралдык сандар менен болгон амалдар]]
+
[[Category:Математика]]

Текущая версия на 08:41, 22 октября 2018


Для натуральных чисел определены следующие действия: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Только в результате двух действий получаются также натуральные числа. Это сложение и умножение.

Deystviya nad natural numbers.gif
Deystviya nad natural numbers.gif

Свойства арифметических действий

Действия сложения, вычитания, умножения и деления называют арифметическими действиями. Они обладают следующими свойствами.

Свойства сложения

1. Переместительное свойство сложения: от перестановки слагаемых сумма не меняется.

a + b = b + a

В этом равенстве a и b могут принимать любые натуральные значения и значение 0.

2. Сочетательное свойство сложения: чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.

В буквенном виде:

(a + b) + c = a + (b + c)

Так как результат сложения трёх чисел не зависит от того как поставлены скобки, то скобки можно не ставить и писать просто a + b + с.

(a + b) + c = a + (b + c) = a + b + c

Переместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм.

3. Свойство нуля при сложении

Сумма двух натуральных чисел всегда больше каждого из слагаемых. Но это не так, если хотя бы одно из слагаемых равно нулю.

Если к числу прибавить нуль, получится само число.

a + О = О + a = a


Example 1 deystviya nad nat numbers.gif
Example 1 deystviya nad nat numbers.gif
В начало

Свойства вычитания

1. Свойство вычитания суммы из числа Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.

a − (b + c) = (a − b) – c или a − (b + c) = (a − с) – b

2. Скобки в выражении (a − b) − c не имеют значения и их можно опустить.

(a − b) − c = a − b – c

3. Свойство вычитания числа из суммы

Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.

(a+b)−c=(a−c)+b (если a>c или а=с) или (a + b) − c = (b − c) + a (если b > c или b = с)

4. Свойство нуля при вычитании Если из числа вычесть нуль, получится само число.

a − О = a

Если из числа вычесть само число, то получится нуль.

a − a = О
Example 2 Deystviya nad nat numbers.gif
Example 2 Deystviya nad nat numbers.gif
В начало

Свойство умножения

1. Переместительное свойство умножения От перестановки множителей произведение не меняется.

a • b = b • a

2. Сочетательное свойство умножения Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

a • (b • c) = (a • b) • c

3. Свойство нуля при умножении Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

a ∙ О = a
О • a • b • c = О

Распределительное свойство умножения относительно сложения

Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.

(a + b) • c = a • c + b • c

Это свойство справедливо для любого количества слагаемых.

(a + b + с + d) • k = a • k + b • k + c • k + d • k

Распределительное свойство умножения относительно вычитания

1. Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе. В буквенном виде свойство записывается так:

(a − b) • c = a • c − b • c

2. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

Example 3 Deystviya nad nat numbers.gif
Example 3 Deystviya nad nat numbers.gif
В начало

Свойство деления

1. Ни одно число нельзя делить на ноль.

2. При делении нуля на число получается ноль.

О : a = О

3. При делении любого числа на 1 получается это же число.

b : 1 = b

4. Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

a : b = (a • k) : (b • k), где k — любое натуральное число.
Example 4 Deystviya nad nat numbers.gif
Example 4 Deystviya nad nat numbers.gif
В начало

Примеры в несколько действий

Примеры могут включать различные действия. Существуют определенные правила, которых придерживаются, когда имеют дело с примерами в несколько действий.

Если пример включает только сложение и вычитание, порядок действий не имеет значения. Однако важно помнить, что знак «+» или «-» применим только к числу, стоящему непосредственно перед ним.

Например, 7 – 5 + 10. Это то же самое, что 7 + 10 – 5 или – 5 + 7 + 10.

Если имеются еще какие - либо действия, используется определенный порядок выполнения.

Порядок выполнения действий в выражениях

В выражениях, содержащих различные действия, сначала выполняется действие в скобках, затем последовательно по уменьшению старшинства: возведение в степень – деление – умножение – сложение – вычитание.

Example poryadok act.png
Example poryadok act.png
В начало

Глоссарий

Действие – это математический процесс, в котором по некоторому правилу и двум данным числам определяют третье число.

Сво́йство — атрибут предмета (объекта).

Степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a. a∙a ∙ a∙…∙a=an

Корнем n - й степени из числа a называется такое число b, где bn=a, где n>1

В начало

Полезные ссылки

А знаете ли вы, что раньше за незнание математики, человека могли просто уволить с работы? Нет?! Тогда стоит посмотреть передачу об истории возникновения таблицы умножения. Профессор рассказывает об интересном методе умножения в Древнем Египте, знакомит с «пальцевым» способом умножения на девять. Кроме того, проводится связь между геометрией и строительством пчелиных сот. Весёлая задачка посвящена умножению. : [Электронный ресурс] //Академия Занимательных Наук YouTube, 2017. https://www.youtube.com/watch?v=vcKD1SURjfg . (дата обращения: 20.11.2017)

В начало

Библиография

  • Приемы быстрых вычислений. Штраус А. П.: [Электронный ресурс] // metod-kopilka.ru 2007-2017 URL: https://www.metod-kopilka.ru/priemi-bistrih-vichisleniy-61445.html. (дата обращения: 20.11.2017)
  • Системы измерения и счет у кыргызов.: [Электронный ресурс] //Open.kg Открытый Кыргызстан. URL: https://www.open.kg/about-kyrgyzstan/culture/ethnography/1970-sistemy-izmereniya-i-schet-u-kyrgyzov.html . (дата обращения: 20.11.2017)
  • Видео «Как научиться быстро считать в уме?: [Электронный ресурс] // Простая математика YouTube, 2017. https://www.youtube.com/watch?v=hEVPZy4xaVQ. (дата обращения: 20.11.2017)
  • Математика 51. История таблицы умножения в древнем Египте — Академия занимательных наук.: [Электронный ресурс] //Академия Занимательных Наук YouTube, 2017. https://www.youtube.com/watch?v=vcKD1SURjfg . (дата обращения: 20.11.2017)
  • В.А. Гусев, А.Г. Мордкович Математика. Справочные материалы М.: Просвещение, 1988.
  • Математика : Новый полный справочник для подготовки к ОГЭ / А.Г. Мерзляк, В.Б. Полонский,М.С. Якир. — Москва : АСТ, 2017. — 447,[1] с.
  • Кроссворды для школьников. Математика. Мантуленко В.Г., Гетменко О.Г. –Ярославль: «Академия развития», 1998. – 144 с.
В начало

Математика в национальных играх кыргызов
П

отребность в измерении и счете родилась у кыргызов в условиях относительно высокоразвитого их общественного производства и социальной дифференциации общества. В киргизском народе до сих пор своеобразно уживаются несколько систем счета, что свидетельствует о различных их источниках. Были известны четыре арифметические действия: сложение, вычитание, умножение, деление. Нечетное число они называли алым эсеп, а четное — туюк эсеп. Эти элементарные математические знания были необходимы им в практической жизни. В национальной игре ордо (эмоциональная игра у взрослых кыргызов, воспроизводящая бой за захват ханской ставки), в детской игре в альчики математические действия сложения, умножения в уме производили с помощью понятия бирдин үчү— пять; бирдин үчү— пять альчиков, бирдин үчү бир — шесть альчиков, бирдин үчү эки — семь альчиков, экинин үчү — десять альчиков, экинин үчү торт — четырнадцать альчиков, бештин үчү — двадцать пять альчиков, кырктын үчү — двести альчиков.

Национальная игра в альчики

Древняя игра кыргызов «Тогуз кумалак» или «Тогуз коргоол» (девять маленьких орешков или фишек) представляет собой деревянную доску с 18 маленькими лунками (в каждой по 9 фишек) для непосредственной игры и большими лунками для выигранных фишек (орешков):

Эки атасы бар,

Он сегиз энеси бар.
Бир жуз алтымыш эки баласы бар.

Имеет двух отцов,
Имеет восемнадцать матерей
И детей - сто шестьдесят два

Процесс игры заключался в следующем: два партнера поочередно раскладывали фишки по кругу. Выигранные фишки собирали в свои кассы-лунки. Игра требовала от каждого играющего большой воли и усидчивости, а главное огромного умственного напряжения. В процессе игры соперники в уме молниеносно вычисляли следующий ход или замысел своего соперника, при этом используя все четыре арифметических действия одновременно.

Расчет и тактика игроков заключались в том, что каждый из них не должен сделать ошибочного хода и тем самым дать возможность другой стороне собрать большое количество фишек. Кто из двух играющих соперников обладал аналитическим умом и тактикой хитроумных ходов, тот и становился победителем.

«Тогуз кумалак» или «Тогуз коргоол»

Другая, более сложная чем «Тогуз кумалак» игра древних кыргызов именовалась «Чатыраш»:

Есть фишки у меня, есть и у тебя,—

Всего их будет тридцать две.

Умный из умных отгадает эту загадку.

В народе существует версия, что эту очень сложную игру кыргызов в прошлые века усовершенствовали индийцы и создали шахматы в сегодняшнем понимании. Поэтому участие в этой интеллектуальной игре принимали в основном взрослые люди и особенно ханы, беки, аскер башчылар — военачальники, эсепчи.

Как научиться быстро считать?

Как научится быстро считать?

Вы спросите, зачем такие сложности? Ведь есть калькулятор в мобильном телефоне. Да, без проблем, но представьте ситуацию, телефон разрядился, или вы не хотите показаться глупым человеком в магазине и хотите правильно получить сдачу? Тогда предлагаем посмотреть видео сюжет, где раскроют секреты, как научится быстро считать.

Кроссворд

Что такое кроссворд? Кроссвордом принято называть интеллектуальную игру со словами. Она помогает развивать память, учит культуре мышления и искать недостающую информацию. Во время разгадывания кроссворда вы закрепляете полученные знания, а также у вас работает деятельное запоминание, что помогает эффективно усвоить материал.

Итак, вписав все слова, в клетки по вертикали, вы получите название арифметического действия над числами.

  • New krossword.jpg
  • Krossword deystviya nad nat numbers.jpg
Волшебные числа в произведениях устного народного творчества

Веками народ создавал мудрые изречения – пословицы и поговорки. В них из поколения в поколение передавались главные мысли о жизни. А использование чисел в поговорках и пословицах отражает развитие цифрового счета у людей с древних времен. Зачастую пословицы с числами имеют особое значение, так как каждая цифра обозначала ранее некое сакральное понятие.

В пословицах могут встречаться самые разные числа, но чаще всего фигурируют цифры от 1 до 9. Их значение может быть самым разным и характеризовать конфликтные ситуации. Типичным примером служит такое изречение: «один в поле не воин». Оно показывает, что каким бы ни был умелым и сильным человек, с проблемой он сможет справиться только при помощи кого-то еще.

Предлагаем вашему вниманию самые распространенные пословицы и поговорки с числами. Подумайте, какой смысл они несут.

  • Poslovicy i pogovorki 1-3.jpg
  • Poslovicy i pogovorki 4 6.jpg
  • Poslovicy i pogovorki 7 9.jpg
Пройди тестирование
Пройди тестирование
Источник — «https://bb.edu.gov.kg/index.php?title=Математика:_Действия_над_натуральными_числами&oldid=27419»