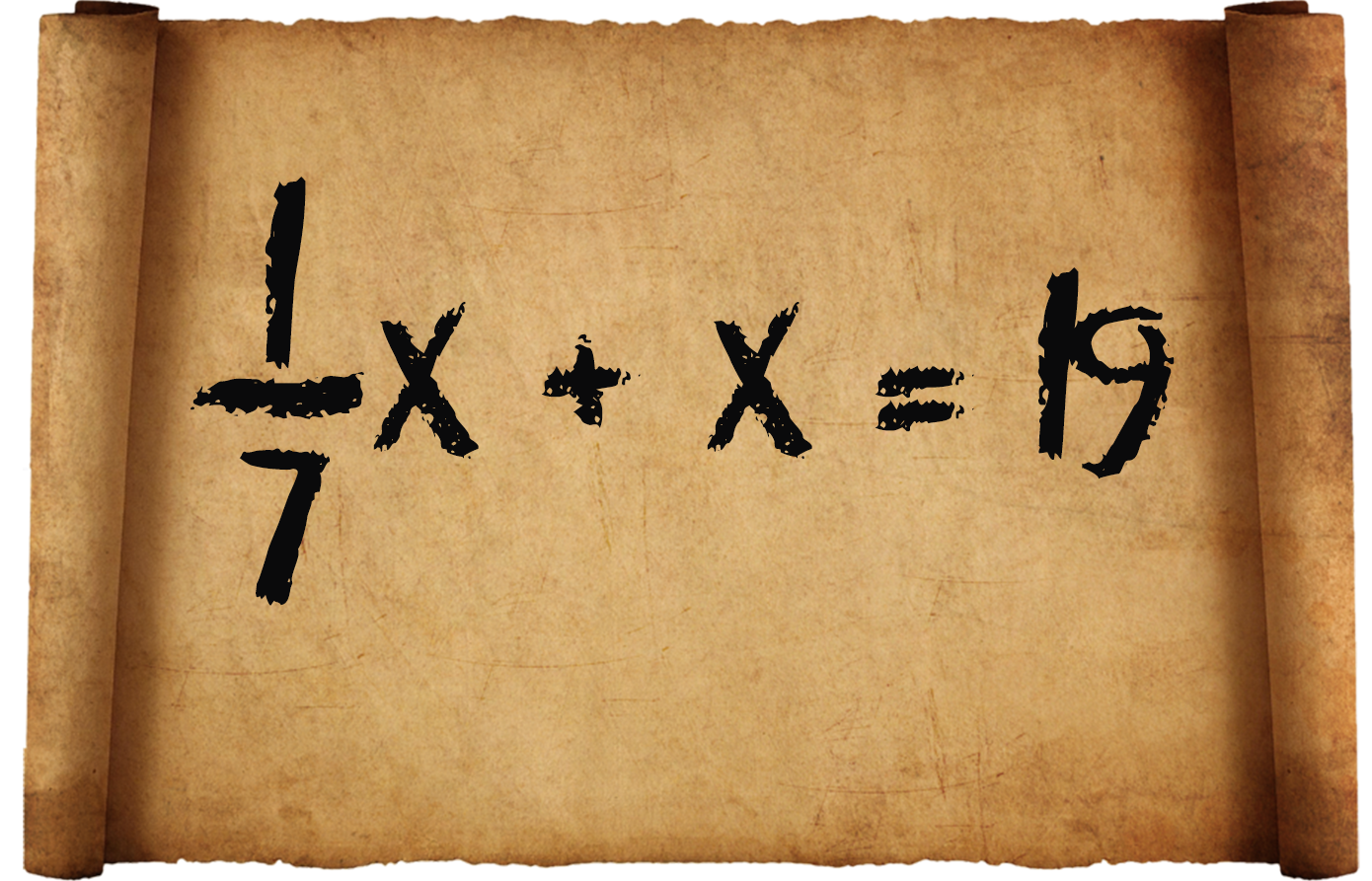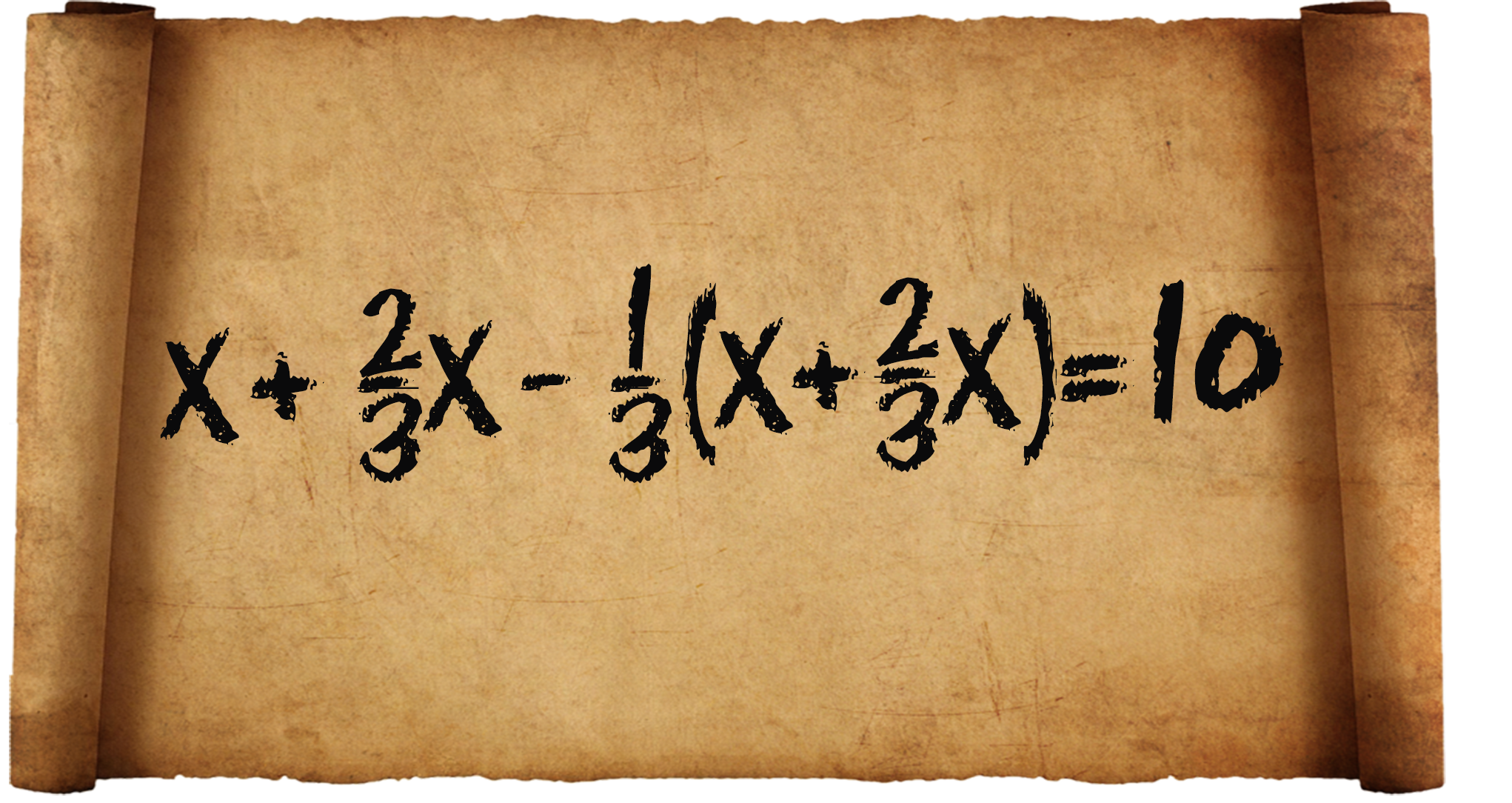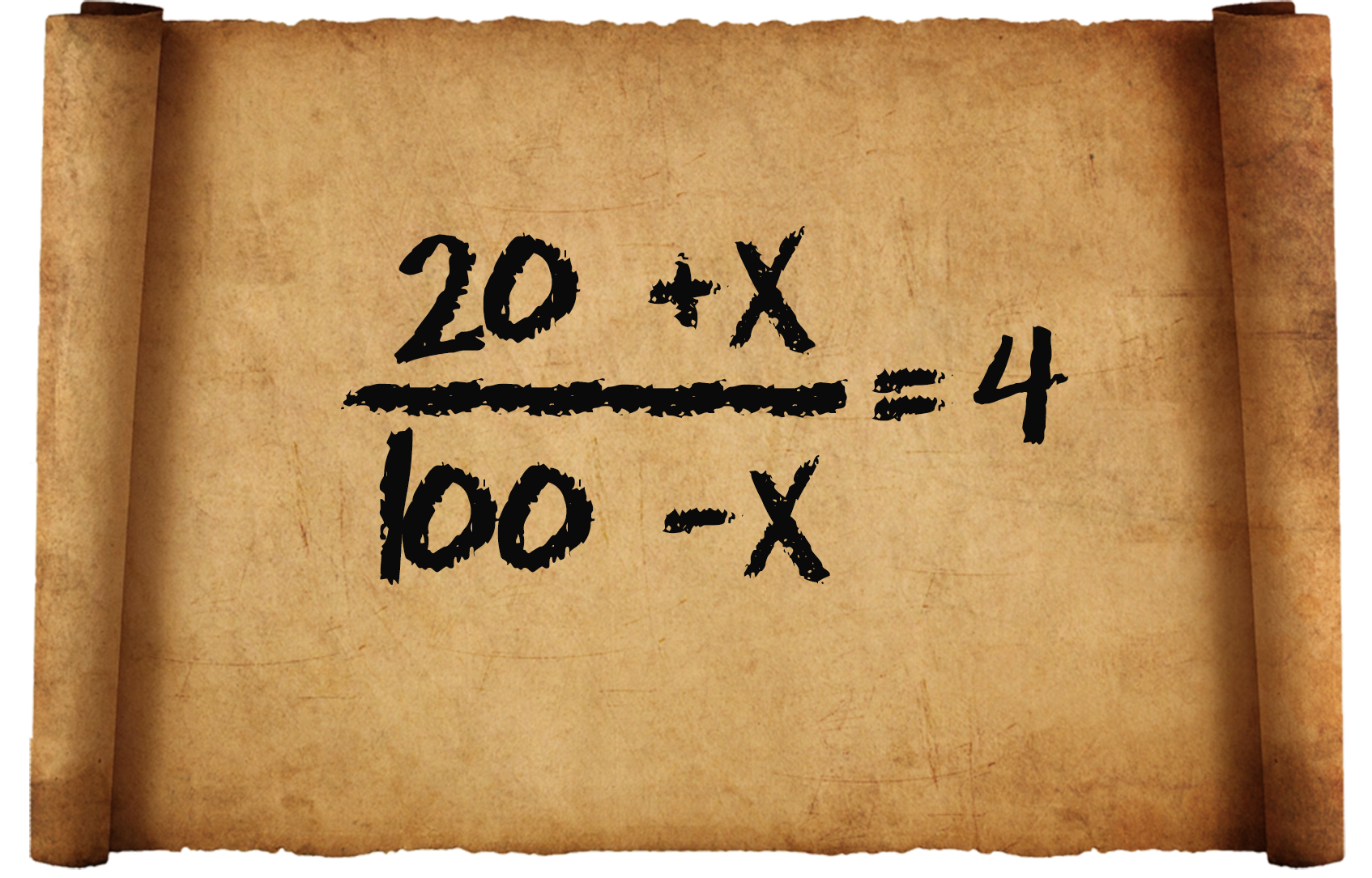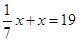Математика: Решение уравнений — различия между версиями
Msu05 (обсуждение | вклад) (→Глоссарий) |
Msu05 (обсуждение | вклад) (→Библиография) |
||
| Строка 137: | Строка 137: | ||
== Библиография == | == Библиография == | ||
| − | * | + | * Математическая модель. Правила http://school-assistant.ru/?predmet=algebra&theme=matemat_model |
| − | * | + | * Основные математические знаки и символы: [Электронный ресурс] // 2013-2018 «SYL.ru» URL: https://www.syl.ru/article/327248/osnovnyie-matematicheskie-znaki-i-simvolyi (дата обращения: 26. 04. 2018) |
| − | * | + | * Институт математики.:[Электронный ресурс] // 2016-2017 Национальная академия наук КР URL:http://naskr.kg/index.php/ru/struktura-nan-kr/nauchno-issledovatelskie-uchrezhdeniya/institut-matematiki (дата обращения: 28. 04. 2018) |
| + | * Линейное Уравнение - Решение С Помощью Онлайн Решателя:[Электронный ресурс] // © Pocket Teacher. https://pocketteacher.ru/linear-equations-2-ru (дата обращения: 28. 04. 2018) | ||
| + | * Развитие математической науки Кыргызстана:[Электронный ресурс] //2018 © Институт Математики URL: http://math.aknet.kg/home/science-develop.pdf | ||
| + | * В.А. Гусев, А.Г. Мордкович Математика. Справочные материалы М.: Просвещение, 1988. | ||
| + | * Федин С. Н. Математики тоже шутят. — 4-е изд. — М.: УРСС, 2012. — 216 с. | ||
| + | |||
<div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | <div class="light" style="float:right;>[[#Начало|В начало]]</div><br clear=all /> | ||
Версия 15:56, 2 мая 2018
_NOTOC__
Содержание
Из истории уравнений
Уравнения для меня важнее, потому что политика — для настоящего, а уравнения — для вечности. Альберт Эйнштейн
Еще в глубокой древности в математических сочинениях встречались уравнения, а также задачи, решаемые с помощью уравнений. Так, в египетском папирусе около 2000 лет до нашей эры (причем, как указывает в нем автор, писец Ахмес, это математическое сочинение является копией с другого, более древнего сочинения) имелись задачи на отыскание неизвестного числа. Это неизвестное называлось «хау» (куча) и обозначалось особым иероглифом.
Современная запись старинных задач
Вот примеры задач из этого папируса.
1) «Неизвестное, его седьмая часть, его целое составляет 19».
В современном виде задача запишется так:
2) «![]() сложено и
сложено и ![]() отнята: остаток 10».
Судя по приведённому в папирусе решению, задачу следует понимать так: к неизвестному прибавлено
отнята: остаток 10».
Судя по приведённому в папирусе решению, задачу следует понимать так: к неизвестному прибавлено ![]() его и отнята
его и отнята ![]() полученной суммы; остаток 10; найти число.
Задача в современном виде запишется так:
полученной суммы; остаток 10; найти число.
Задача в современном виде запишется так: ![]() ; Ответ: х=9
; Ответ: х=9
3) У Диофанта также встречаются уравнения с одним неизвестным, например:
«Числа 20 и 100. Нужно одно и то же число прибавить к меньшему и вычесть из большего; отношение суммы к разности равно 4».
Задача приводит к уравнению: ![]()
4) В индийской рукописной арифметике VII и VIII века нашей эры, являющейся копией с более древней рукописи (III-IV века), имеется такая задача:
«Из четырех жертвователей второй дал вдвое больше первого, третий втрое больше второго, четвертый вчетверо больше третьего, а все вместе дали 132. Сколько дал первый?»
Получаем уравнение:
В рукописи задача решается способом «ложного положения». (Этим способом пользовался и Л.Ф. Магницкий в своей «Арифметике».)
«Если бы первый дал 1, то второй бы 2, третий 6, четвертый 24, а все вместе 33. Но всего было 132, то есть вчетверо больше. Значит, и каждый из жертвователей дал вчетверо больше».
Ответ: 4; 8; 24; 96.
Но общее правило для решения уравнений первой степени с одним неизвестным дал в IX веке Мухаммед аль-Хорезми.
В своем сочинении «Аль-джебр и аль-мукабала» он дает два приема, применяемых при решении уравнений.
1) Прием «аль-джебр» заключается в том, что если имеются в уравнении отрицательные (вычитаемые) члены, то следует прибавить противоположные им члены к обеим частям уравнения, и тогда все члены будут положительными.
2) Прием «аль-мукабала» заключается в вычитании из обеих частей уравнения одинаковых членов, что приводит к его упрощению.
Например, дано уравнение: 5х-17=2х-5 Применим «аль-джебр»: прибавляем к каждой части уравнения 5 и 17. Получим: 5х+5=2х+17 Применим «аль-мукабала»: вычитаем из каждой части 2x и 5. Получим: 3х=12 Отсюда легко находится х.
Развитие математической науки в Кыргызстане
Математика как школьный предмет начала изучаться в Кыргызстане только после Октябрьской революции, а высшая математика - после открытия первого в Кыргызстане ВУЗа - Кыргызского государственного педагогического института - ныне Кыргызского национального университета им. Ж. Баласагына.
Систематические исследования по математике в Кыргызстане начались в 1940 году, на семинаре под руководством профессора Г.А. Сухомлинова. В 1949-1965 годы семинаром руководил профессор Я.В. Быков, ставший в 1960 году членом-корреспондентом АН Киргизской ССР, с 1966 г. этот семинар, ставший уже общереспубликанским, в стенах Института возглавил М.И. Иманалиев, академик АН Киргизской ССР (1979) и член-корреспондент АН СССР (1981 год).
В 1955 году был организован Отдел физики, математики и механики при Президиуме АН Киргизской ССР, в составе которого были, тогда еще кандидаты наук, Я.В. Быков и М.И. Иманалиев. В 1960 году Отдел был преобразован в Институт физики, математики и механики. В 1962 году он стал называться Институтом физики и математики, а в 1984 году на базе математических лабораторий Института физики и математики был организован Институт математики. На его базе в 2008 году был создан Институт теоретической и прикладной математики, а с 11 мая 2017 года он переименован в Институт математики НАН КР.
С 1984 года по 2016 год Институтом руководил академик М.И. Иманалиев, с 2016 года по настоящее время руководителем Института является академик А.А. Борубаев.
Деятельность Института определяется следующими основными направлениями научных исследований:
- Равномерные и топологические пространства и их отображения.
- Функциональные пространства.
- Динамические системы, описываемые разностными, дифференциальными и интегро-дифференциальными уравнениями, в том числе сингулярно-возмущенными.
- Интегральные уравнения, некорректные и обратные задачи.
- Оптимизационные экономические задачи.
- Компьютеризация научных исследований, интерактивное представление объектов.
Особое внимание уделяется исследованию по теории и приложениям интегро-дифференциальных, интегральных и дифференциальных уравнений, операционному исчислению, по разностным и суммарно-разностным уравнениям, математической физике, линейной алгебре. Больших успехов математика Кыргызстана достигла в области интегро-дифференциальных уравнений. Ученые математики надеются, что в математическую науку придут образованные, высокоинтеллектуальные, целеустремленные молодые люди и поднимут престиж математической науки Кыргызстана еще выше.
Полезные ссылки
Первоначальные способы решения уравнений были достаточно сложными и разнообразными. В процессе развития математики произошло их значительное упрощение, и для каждого типа уравнений появился единый алгоритм решения. Более подробно можете увидеть: https://www.youtube.com/watch?v=WpwOQHVB5s4
Глоссарий
- Алгебра – это раздел математики, который изучает общие свойства действий над различными величинами и решение уравнений, связанных с этими действиями.
- Веще́ственное число (от лат. realis — действительный) — математический объект, возникший из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких вычислительных операций, как извлечение корня, вычисление логарифмов, решение алгебраических уравнений, исследование поведения функци
- Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
- Теоре́ма (др.-греч. θεώρημα — «доказательство, вид; взгляд; представление, положение») — утверждение, выводимое в рамках рассматриваемой теории из множества аксиом посредством использования конечного множества правил вывода.
- Теорема Виета: сумма корней приведенного квадратного уравнения x2+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену: x1+x2=-p; x1∙x2=q.
Библиография
- Математическая модель. Правила http://school-assistant.ru/?predmet=algebra&theme=matemat_model
- Основные математические знаки и символы: [Электронный ресурс] // 2013-2018 «SYL.ru» URL: https://www.syl.ru/article/327248/osnovnyie-matematicheskie-znaki-i-simvolyi (дата обращения: 26. 04. 2018)
- Институт математики.:[Электронный ресурс] // 2016-2017 Национальная академия наук КР URL:http://naskr.kg/index.php/ru/struktura-nan-kr/nauchno-issledovatelskie-uchrezhdeniya/institut-matematiki (дата обращения: 28. 04. 2018)
- Линейное Уравнение - Решение С Помощью Онлайн Решателя:[Электронный ресурс] // © Pocket Teacher. https://pocketteacher.ru/linear-equations-2-ru (дата обращения: 28. 04. 2018)
- Развитие математической науки Кыргызстана:[Электронный ресурс] //2018 © Институт Математики URL: http://math.aknet.kg/home/science-develop.pdf
- В.А. Гусев, А.Г. Мордкович Математика. Справочные материалы М.: Просвещение, 1988.
- Федин С. Н. Математики тоже шутят. — 4-е изд. — М.: УРСС, 2012. — 216 с.
Математика – как высокая винтовая лестница,
чтобы взойти по ней к вершинам знаний,
надо пройти каждую ступеньку от первой до последней.
Школьник зашел в лавочку возле школы. На прилавке лежали ручки по 30 рублей за штуку и карандаши по 15 рублей. Мальчик приобрел один карандаш и пошел к выходу, но по дороге подумал: «Я уже отдал продавцу 15 рублей, значит, если вернуть покупку, в сумме на моем счету окажется 30 руб». Сможет ли школьник теперь купить ручку? Почему?
Ответ
Не сможет.
В качестве объяснения приведем небольшую шутку.
Студент заказал в кафе булочку, но затем решил, что не слишком голоден и обменял ее на чашечку кофе. Выпив напиток, он направился к выходу, не расплатившись. Cамо собой, за ним побежала буфетчица.
- Вы не заплатили за кофе!
- Да, все верно, но я же взял его взамен булочки!
- Так булка тоже не оплачена!
- Верно, но я ведь ее и не ел!